Teoría de la deformación infinitesimal

ImprimirCitar

Modelo matemático para describir la deformación del material bajo estrés

En mecánica continua, la teoría de la deformación infinitesimal es un enfoque matemático para la descripción de la deformación de un cuerpo sólido en el que se supone que los desplazamientos de las partículas materiales son mucho más pequeños (de hecho, infinitesimalmente menor) que cualquier dimensión relevante del cuerpo; de modo que se puede suponer que su geometría y las propiedades constitutivas del material (como la densidad y la rigidez) en cada punto del espacio no cambian debido a la deformación.

Con esta suposición, las ecuaciones de la mecánica continua se simplifican considerablemente. Este enfoque también puede denominarse teoría de pequeñas deformaciones, teoría de pequeños desplazamientos o teoría de pequeños desplazamientos-gradiente. Se contrasta con la teoría de la deformación finita donde se hace la suposición opuesta.

La teoría de la deformación infinitesimal se adopta comúnmente en ingeniería civil y mecánica para el análisis de tensión de estructuras construidas con materiales elásticos relativamente rígidos como el hormigón y el acero, ya que un objetivo común en el diseño de tales estructuras es minimizar su deformación bajo cargas típicas.. Sin embargo, esta aproximación exige precaución en el caso de cuerpos delgados y flexibles, como varillas, placas y corazas que son susceptibles de rotaciones significativas, lo que hace que los resultados no sean confiables.

Tensor de deformación infinitesimal

Para Deformaciones infinitesimal de un cuerpo continuo, en el que el gradiente de desplazamiento (2a orden tensor) es pequeño en comparación con la unidad, es decir. $|nabla mathbf u| ll 1$ , es posible realizar un linealización geométrica de cualquiera de los tensores de cepa (infinitamente muchos posibles) utilizados en la teoría de cepa finita, por ejemplo, el tensor de cepa lagrangiana $mathbf {E}$ , y el tensor de cepa Euleria ${displaystyle mathbf {e} }$ . En tal linearización, se descuidan los términos no lineales o de segundo orden del tensor de cepa finito. Así tenemos

{displaystyle mathbf {E} ={frac {1}{2}}left(nabla _{mathbf {X} }mathbf {u} +(nabla _{mathbf {X} }mathbf {u})^{T}+(nabla _{mathbf {X} }mathbf {u})^{T}nabla _{mathbf {X} }mathbf {u} right)approx {frac {1}{2}}left(nabla _{mathbf {X} }mathbf {u} +(nabla _{mathbf {X} }mathbf {u})^{T}right)}

{displaystyle E_{KL}={frac {1}{2}}left({frac {partial U_{K}}{partial X_{L}}}+{frac {partial U_{L}}{partial X_{K}}}+{frac {partial U_{M}}{partial X_{K}}}{frac {partial U_{M}}{partial X_{L}}}right)approx {frac {1}{2}}left({frac {partial U_{K}}{partial X_{L}}}+{frac {partial U_{L}}{partial X_{K}}}right)}

{displaystyle mathbf {e} ={frac {1}{2}}left(nabla _{mathbf {x} }mathbf {u} +(nabla _{mathbf {x} }mathbf {u})^{T}-nabla _{mathbf {x} }mathbf {u} (nabla _{mathbf {x} }mathbf {u})^{T}right)approx {frac {1}{2}}left(nabla _{mathbf {x} }mathbf {u} +(nabla _{mathbf {x} }mathbf {u})^{T}right)}

{displaystyle e_{rs}={frac {1}{2}}left({frac {partial u_{r}}{partial x_{s}}}+{frac {partial u_{s}}{partial x_{r}}}-{frac {partial u_{k}}{partial x_{r}}}{frac {partial u_{k}}{partial x_{s}}}right)approx {frac {1}{2}}left({frac {partial u_{r}}{partial x_{s}}}+{frac {partial u_{s}}{partial x_{r}}}right)}

Esta linealización implica que la descripción lagrangiana y la descripción euleriana son aproximadamente iguales, ya que hay poca diferencia en las coordenadas materiales y espaciales de un punto material dado en el continuo. Por lo tanto, los componentes del gradiente de desplazamiento de material y los componentes del gradiente de desplazamiento espacial son aproximadamente iguales. Así tenemos

{displaystyle mathbf {E} approx mathbf {e} approx {boldsymbol {varepsilon }}={frac {1}{2}}left((nabla mathbf {u})^{T}+nabla mathbf {u} right)}

{displaystyle E_{KL}approx e_{rs}approx varepsilon _{ij}={frac {1}{2}}left(u_{i,j}+u_{j,i}right)}

varepsilon _{ij}

Tensor de cepa infinitesimal

{displaystyle {boldsymbol {varepsilon }}}

Tensor de cepa de Cauchytensor linealpequeño tensor de tensión

{displaystyle {begin{aligned}varepsilon _{ij}&={frac {1}{2}}left(u_{i,j}+u_{j,i}right)\&={begin{bmatrix}varepsilon _{11}&varepsilon _{12}&varepsilon _{13}\varepsilon _{21}&varepsilon _{22}&varepsilon _{23}\varepsilon _{31}&varepsilon _{32}&varepsilon _{33}\end{bmatrix}}\&={begin{bmatrix}{frac {partial u_{1}}{partial x_{1}}}&{frac {1}{2}}left({frac {partial u_{1}}{partial x_{2}}}+{frac {partial u_{2}}{partial x_{1}}}right)&{frac {1}{2}}left({frac {partial u_{1}}{partial x_{3}}}+{frac {partial u_{3}}{partial x_{1}}}right)\{frac {1}{2}}left({frac {partial u_{2}}{partial x_{1}}}+{frac {partial u_{1}}{partial x_{2}}}right)&{frac {partial u_{2}}{partial x_{2}}}&{frac {1}{2}}left({frac {partial u_{2}}{partial x_{3}}}+{frac {partial u_{3}}{partial x_{2}}}right)\{frac {1}{2}}left({frac {partial u_{3}}{partial x_{1}}}+{frac {partial u_{1}}{partial x_{3}}}right)&{frac {1}{2}}left({frac {partial u_{3}}{partial x_{2}}}+{frac {partial u_{2}}{partial x_{3}}}right)&{frac {partial u_{3}}{partial x_{3}}}\end{bmatrix}}end{aligned}}}

{displaystyle {begin{bmatrix}varepsilon _{xx}&varepsilon _{xy}&varepsilon _{xz}\varepsilon _{yx}&varepsilon _{yy}&varepsilon _{yz}\varepsilon _{zx}&varepsilon _{zy}&varepsilon _{zz}\end{bmatrix}}={begin{bmatrix}{frac {partial u_{x}}{partial x}}&{frac {1}{2}}left({frac {partial u_{x}}{partial y}}+{frac {partial u_{y}}{partial x}}right)&{frac {1}{2}}left({frac {partial u_{x}}{partial z}}+{frac {partial u_{z}}{partial x}}right)\{frac {1}{2}}left({frac {partial u_{y}}{partial x}}+{frac {partial u_{x}}{partial y}}right)&{frac {partial u_{y}}{partial y}}&{frac {1}{2}}left({frac {partial u_{y}}{partial z}}+{frac {partial u_{z}}{partial y}}right)\{frac {1}{2}}left({frac {partial u_{z}}{partial x}}+{frac {partial u_{x}}{partial z}}right)&{frac {1}{2}}left({frac {partial u_{z}}{partial y}}+{frac {partial u_{y}}{partial z}}right)&{frac {partial u_{z}}{partial z}}\end{bmatrix}}}

Además, dado que el gradiente de deformación puede expresarse como ${boldsymbol {F}}={boldsymbol {nabla }}{mathbf {u}}+{boldsymbol {I}}$ Donde ${boldsymbol {I}}$ es el segundo tensor de identidad, tenemos

{displaystyle {boldsymbol {varepsilon }}={frac {1}{2}}left({boldsymbol {F}}^{T}+{boldsymbol {F}}right)-{boldsymbol {I}}}

Además, a partir de la expresión general para los tensores de deformación finitos de Lagrangian y Euler, tenemos

{displaystyle {begin{aligned}mathbf {E} _{(m)}&={frac {1}{2m}}(mathbf {U} ^{2m}-{boldsymbol {I}})={frac {1}{2m}}[({boldsymbol {F}}^{T}{boldsymbol {F}})^{m}-{boldsymbol {I}}]approx {frac {1}{2m}}[{{boldsymbol {nabla }}mathbf {u} +({boldsymbol {nabla }}mathbf {u})^{T}+{boldsymbol {I}}}^{m}-{boldsymbol {I}}]approx {boldsymbol {varepsilon }}\mathbf {e} _{(m)}&={frac {1}{2m}}(mathbf {V} ^{2m}-{boldsymbol {I}})={frac {1}{2m}}[({boldsymbol {F}}{boldsymbol {F}}^{T})^{m}-{boldsymbol {I}}]approx {boldsymbol {varepsilon }}end{aligned}}}

Derivación geométrica

Gráfico 1. Deformación geométrica bidimensional de un elemento material infinitesimal.

Considere una deformación bidimensional de un elemento de material rectangular infinitesimal con dimensiones $dx$ por $dy$ (Figura 1), que después de la deformación, toma la forma de un rhombus. De la geometría de la Figura 1 tenemos

{displaystyle {begin{aligned}{overline {ab}}&={sqrt {left(dx+{frac {partial u_{x}}{partial x}}dxright)^{2}+left({frac {partial u_{y}}{partial x}}dxright)^{2}}}\&=dx{sqrt {1+2{frac {partial u_{x}}{partial x}}+left({frac {partial u_{x}}{partial x}}right)^{2}+left({frac {partial u_{y}}{partial x}}right)^{2}}}\end{aligned}}}

Para los gradientes de desplazamiento muy pequeño, es decir, $|nabla mathbf u| ll 1$ , tenemos

{displaystyle {overline {ab}}approx dx+{frac {partial u_{x}}{partial x}}dx}

La tensión normal en la $x$ -dirección del elemento rectangular se define por

{displaystyle varepsilon _{x}={frac {{overline {ab}}-{overline {AB}}}{overline {AB}}}}

{displaystyle {overline {AB}}=dx}

{displaystyle varepsilon _{x}={frac {partial u_{x}}{partial x}}}

Del mismo modo, la cepa normal en la $y$ - dirección, y $z$ - dirección, se convierte en

{displaystyle varepsilon _{y}={frac {partial u_{y}}{partial y}}quadqquad varepsilon _{z}={frac {partial u_{z}}{partial z}}}

La cepa de corte de ingeniería, o el cambio en ángulo entre dos líneas de material ortogonal originalmente, en esta línea de caso ${displaystyle {overline {AC}}}$ y ${displaystyle {overline {AB}}}$ , se define como

{displaystyle gamma _{xy}=alpha +beta }

De la geometría de la Figura 1 tenemos

{displaystyle tan alpha ={frac {{dfrac {partial u_{y}}{partial x}}dx}{dx+{dfrac {partial u_{x}}{partial x}}dx}}={frac {dfrac {partial u_{y}}{partial x}}{1+{dfrac {partial u_{x}}{partial x}}}}quadqquad tan beta ={frac {{dfrac {partial u_{x}}{partial y}}dy}{dy+{dfrac {partial u_{y}}{partial y}}dy}}={frac {dfrac {partial u_{x}}{partial y}}{1+{dfrac {partial u_{y}}{partial y}}}}}

Para pequeñas rotaciones, es decir, $alpha$ y $beta$ son ${displaystyle ll 1}$ tenemos

{displaystyle tan alpha approx alpha quadqquad tan beta approx beta }

{displaystyle alpha ={frac {partial u_{y}}{partial x}}quadqquad beta ={frac {partial u_{x}}{partial y}}}

{displaystyle gamma _{xy}=alpha +beta ={frac {partial u_{y}}{partial x}}+{frac {partial u_{x}}{partial y}}}

x

y

u_{x}

u_{y}

{displaystyle gamma _{xy}=gamma _{yx}}

Del mismo modo, para el $y$ - $z$ y $x$ - $z$ aviones, tenemos

{displaystyle gamma _{yz}=gamma _{zy}={frac {partial u_{y}}{partial z}}+{frac {partial u_{z}}{partial y}}quadqquad gamma _{zx}=gamma _{xz}={frac {partial u_{z}}{partial x}}+{frac {partial u_{x}}{partial z}}}

Se puede ver que los componentes de cepa de tijera diezsorial del tensor de cepa infinitesimal se pueden expresar utilizando la definición de cepa de ingeniería, $gamma$ , como

{displaystyle {begin{bmatrix}varepsilon _{xx}&varepsilon _{xy}&varepsilon _{xz}\varepsilon _{yx}&varepsilon _{yy}&varepsilon _{yz}\varepsilon _{zx}&varepsilon _{zy}&varepsilon _{zz}\end{bmatrix}}={begin{bmatrix}varepsilon _{xx}&gamma _{xy}/2&gamma _{xz}/2\gamma _{yx}/2&varepsilon _{yy}&gamma _{yz}/2\gamma _{zx}/2&gamma _{zy}/2&varepsilon _{zz}\end{bmatrix}}}

Interpretación física

De la teoría de la deformación finita tenemos

{displaystyle dmathbf {x} ^{2}-dmathbf {X} ^{2}=dmathbf {X} cdot 2mathbf {E} cdot dmathbf {X} quad {text{or}}quad (dx)^{2}-(dX)^{2}=2E_{KL},dX_{K},dX_{L}}

Para deformaciones infinitesimales entonces tenemos

{displaystyle dmathbf {x} ^{2}-dmathbf {X} ^{2}=dmathbf {X} cdot 2mathbf {boldsymbol {varepsilon }} cdot dmathbf {X} quad {text{or}}quad (dx)^{2}-(dX)^{2}=2varepsilon _{KL},dX_{K},dX_{L}}

Dividiendo por ${displaystyle (dX)^{2}}$ tenemos

{displaystyle {frac {dx-dX}{dX}}{frac {dx+dX}{dX}}=2varepsilon _{ij}{frac {dX_{i}}{dX}}{frac {dX_{j}}{dX}}}

Para pequeñas deformaciones asumimos que ${displaystyle dxapprox dX}$ , por lo tanto el segundo término del lado izquierdo se convierte en: ${displaystyle {frac {dx+dX}{dX}}approx 2}$ .

Entonces tenemos

{displaystyle {frac {dx-dX}{dX}}=varepsilon _{ij}N_{i}N_{j}=mathbf {N} cdot {boldsymbol {varepsilon }}cdot mathbf {N} }

{displaystyle N_{i}={frac {dX_{i}}{dX}}}

{displaystyle dmathbf {X} }

{displaystyle e_{(mathbf {N})}}

{mathbf N}

{mathbf N}

X_{1}

{displaystyle mathbf {N} =mathbf {I} _{1}}

{displaystyle e_{(mathbf {I} _{1})}=mathbf {I} _{1}cdot {boldsymbol {varepsilon }}cdot mathbf {I} _{1}=varepsilon _{11}.}

Del mismo modo, ${displaystyle mathbf {N} =mathbf {I} _{2}}$ y ${displaystyle mathbf {N} =mathbf {I} _{3}}$ podemos encontrar las cepas normales ${displaystyle varepsilon _{22}}$ y ${displaystyle varepsilon _{33}}$ , respectivamente. Por lo tanto, los elementos diagonales del tensor de cepa infinitesimal son las cepas normales en las direcciones de coordenadas.

Reglas de transformación de deformaciones

Si elegimos un sistema de coordenadas ortonormal ( $mathbf{e}_1,mathbf{e}_2,mathbf{e}_3$ ) podemos escribir el tensor en términos de componentes con respecto a esos vectores base como

{displaystyle {boldsymbol {varepsilon }}=sum _{i=1}^{3}sum _{j=1}^{3}varepsilon _{ij}mathbf {e} _{i}otimes mathbf {e} _{j}}

{displaystyle {underline {underline {boldsymbol {varepsilon }}}}={begin{bmatrix}varepsilon _{11}&varepsilon _{12}&varepsilon _{13}\varepsilon _{12}&varepsilon _{22}&varepsilon _{23}\varepsilon _{13}&varepsilon _{23}&varepsilon _{33}end{bmatrix}}}

{hat {{mathbf {e}}}}_{1},{hat {{mathbf {e}}}}_{2},{hat {{mathbf {e}}}}_{3}

{displaystyle {boldsymbol {varepsilon }}=sum _{i=1}^{3}sum _{j=1}^{3}{hat {varepsilon }}_{ij}{hat {mathbf {e} }}_{i}otimes {hat {mathbf {e} }}_{j}quad implies quad {underline {underline {hat {boldsymbol {varepsilon }}}}}={begin{bmatrix}{hat {varepsilon }}_{11}&{hat {varepsilon }}_{12}&{hat {varepsilon }}_{13}\{hat {varepsilon }}_{12}&{hat {varepsilon }}_{22}&{hat {varepsilon }}_{23}\{hat {varepsilon }}_{13}&{hat {varepsilon }}_{23}&{hat {varepsilon }}_{33}end{bmatrix}}}

{displaystyle {hat {varepsilon }}_{ij}=ell _{ip}~ell _{jq}~varepsilon _{pq}}

{displaystyle ell _{ij}={hat {mathbf {e} }}_{i}cdot {mathbf {e} }_{j}}

{displaystyle {underline {underline {hat {boldsymbol {varepsilon }}}}}={underline {underline {mathbf {L} }}}~{underline {underline {boldsymbol {varepsilon }}}}~{underline {underline {mathbf {L} }}}^{T}}

{displaystyle {begin{bmatrix}{hat {varepsilon }}_{11}&{hat {varepsilon }}_{12}&{hat {varepsilon }}_{13}\{hat {varepsilon }}_{21}&{hat {varepsilon }}_{22}&{hat {varepsilon }}_{23}\{hat {varepsilon }}_{31}&{hat {varepsilon }}_{32}&{hat {varepsilon }}_{33}end{bmatrix}}={begin{bmatrix}ell _{11}&ell _{12}&ell _{13}\ell _{21}&ell _{22}&ell _{23}\ell _{31}&ell _{32}&ell _{33}end{bmatrix}}{begin{bmatrix}varepsilon _{11}&varepsilon _{12}&varepsilon _{13}\varepsilon _{21}&varepsilon _{22}&varepsilon _{23}\varepsilon _{31}&varepsilon _{32}&varepsilon _{33}end{bmatrix}}{begin{bmatrix}ell _{11}&ell _{12}&ell _{13}\ell _{21}&ell _{22}&ell _{23}\ell _{31}&ell _{32}&ell _{33}end{bmatrix}}^{T}}

Invariantes de deformación

Ciertas operaciones en el tensor de deformación dan el mismo resultado sin tener en cuenta qué sistema de coordenadas ortonormales se utiliza para representar los componentes de deformación. Los resultados de estas operaciones se denominan invariantes de deformación. Las invariantes de deformación más utilizadas son

{displaystyle {begin{aligned}I_{1}&=mathrm {tr} ({boldsymbol {varepsilon }})\I_{2}&={tfrac {1}{2}}{[mathrm {tr} ({boldsymbol {varepsilon }})]^{2}-mathrm {tr} ({boldsymbol {varepsilon }}^{2})}\I_{3}&=det({boldsymbol {varepsilon }})end{aligned}}}

{displaystyle {begin{aligned}I_{1}&=varepsilon _{11}+varepsilon _{22}+varepsilon _{33}\I_{2}&=varepsilon _{11}varepsilon _{22}+varepsilon _{22}varepsilon _{33}+varepsilon _{33}varepsilon _{11}-varepsilon _{12}^{2}-varepsilon _{23}^{2}-varepsilon _{31}^{2}\I_{3}&=varepsilon _{11}(varepsilon _{22}varepsilon _{33}-varepsilon _{23}^{2})-varepsilon _{12}(varepsilon _{21}varepsilon _{33}-varepsilon _{23}varepsilon _{31})+varepsilon _{13}(varepsilon _{21}varepsilon _{32}-varepsilon _{22}varepsilon _{31})end{aligned}}}

Cepas principales

Se puede demostrar que es posible encontrar un sistema de coordenadas ( ${mathbf {n}}_{1},{mathbf {n}}_{2},{mathbf {n}}_{3}$ ) en que los componentes del tensor de tensión son

{displaystyle {underline {underline {boldsymbol {varepsilon }}}}={begin{bmatrix}varepsilon _{1}&0&0\0&varepsilon _{2}&0\0&0&varepsilon _{3}end{bmatrix}}quad implies quad {boldsymbol {varepsilon }}=varepsilon _{1}mathbf {n} _{1}otimes mathbf {n} _{1}+varepsilon _{2}mathbf {n} _{2}otimes mathbf {n} _{2}+varepsilon _{3}mathbf {n} _{3}otimes mathbf {n} _{3}}

{mathbf {n}}_{1},{mathbf {n}}_{2},{mathbf {n}}_{3}

cepas principales

{mathbf {n}}_{i}

Si nos dan los componentes del tensor de deformación en un sistema de coordenadas ortonormal arbitrario, podemos encontrar las deformaciones principales utilizando una descomposición de valores propios determinada al resolver el sistema de ecuaciones

{displaystyle ({underline {underline {boldsymbol {varepsilon }}}}-varepsilon _{i}~{underline {underline {mathbf {I} }}})~mathbf {n} _{i}={underline {mathbf {0} }}}

{mathbf {n}}_{i}

Deformación volumétrica

La dilatación (la variación relativa del volumen) es la primera invariante de deformación o traza del tensor:

{displaystyle delta ={frac {Delta V}{V_{0}}}=I_{1}=varepsilon _{11}+varepsilon _{22}+varepsilon _{33}}

{displaystyle acdot (1+varepsilon _{11})times acdot (1+varepsilon _{22})times acdot (1+varepsilon _{33})}

V₀a³

{displaystyle {frac {Delta V}{V_{0}}}={frac {left(1+varepsilon _{11}+varepsilon _{22}+varepsilon _{33}+varepsilon _{11}cdot varepsilon _{22}+varepsilon _{11}cdot varepsilon _{33}+varepsilon _{22}cdot varepsilon _{33}+varepsilon _{11}cdot varepsilon _{22}cdot varepsilon _{33}right)cdot a^{3}-a^{3}}{a^{3}}}}

{displaystyle 1gg varepsilon _{ii}gg varepsilon _{ii}cdot varepsilon _{jj}gg varepsilon _{11}cdot varepsilon _{22}cdot varepsilon _{33}}

En caso de corte puro, podemos ver que no hay cambio de volumen.

Tensor de desviación de deformación

El tensor de cepa infinitesimal $varepsilon _{ij}$ , similarmente al tensor de estrés de Cauchy, se puede expresar como la suma de otros dos tensores:

a tensor de cepa o tensor de tensión volumétrica o tensor de cepa esférica, ${displaystyle varepsilon _{M}delta _{ij}}$ , relacionado con dilatación o cambio de volumen; y
un componente desviador llamado desviador de tensión tensor, ${displaystyle varepsilon '_{ij}}$ , relacionado con la distorsión.

{displaystyle varepsilon _{ij}=varepsilon '_{ij}+varepsilon _{M}delta _{ij}}

{displaystyle varepsilon _{M}}

{displaystyle varepsilon _{M}={frac {varepsilon _{kk}}{3}}={frac {varepsilon _{11}+varepsilon _{22}+varepsilon _{33}}{3}}={tfrac {1}{3}}I_{1}^{e}}

El tensor de deformación desviador se puede obtener restando el tensor de deformación medio del tensor de deformación infinitesimal:

{displaystyle {begin{aligned} varepsilon '_{ij}&=varepsilon _{ij}-{frac {varepsilon _{kk}}{3}}delta _{ij}\{begin{bmatrix}varepsilon '_{11}&varepsilon '_{12}&varepsilon '_{13}\varepsilon '_{21}&varepsilon '_{22}&varepsilon '_{23}\varepsilon '_{31}&varepsilon '_{32}&varepsilon '_{33}\end{bmatrix}}&={begin{bmatrix}varepsilon _{11}&varepsilon _{12}&varepsilon _{13}\varepsilon _{21}&varepsilon _{22}&varepsilon _{23}\varepsilon _{31}&varepsilon _{32}&varepsilon _{33}\end{bmatrix}}-{begin{bmatrix}varepsilon _{M}&0&0\0&varepsilon _{M}&0\0&0&varepsilon _{M}\end{bmatrix}}\&={begin{bmatrix}varepsilon _{11}-varepsilon _{M}&varepsilon _{12}&varepsilon _{13}\varepsilon _{21}&varepsilon _{22}-varepsilon _{M}&varepsilon _{23}\varepsilon _{31}&varepsilon _{32}&varepsilon _{33}-varepsilon _{M}\end{bmatrix}}\end{aligned}}}

Deformaciones octaédricas

Vamos. ${mathbf {n}}_{1},{mathbf {n}}_{2},{mathbf {n}}_{3}$ ) sean las direcciones de las tres cepas principales. An avión octadral es uno cuya normalidad hace iguales ángulos con las tres direcciones principales. La cepa de la ingeniería en un plano octaedral se llama la octadral shear cepa y se da por

{displaystyle gamma _{mathrm {oct} }={tfrac {2}{3}}{sqrt {(varepsilon _{1}-varepsilon _{2})^{2}+(varepsilon _{2}-varepsilon _{3})^{2}+(varepsilon _{3}-varepsilon _{1})^{2}}}}

varepsilon _{1},varepsilon _{2},varepsilon _{3}

La deformación normal en un plano octaédrico viene dada por

{displaystyle varepsilon _{mathrm {oct} }={tfrac {1}{3}}(varepsilon _{1}+varepsilon _{2}+varepsilon _{3})}

Deformación equivalente

Una cantidad escalar denominada deformación equivalente, o la deformación equivalente de von Mises, se utiliza a menudo para describir el estado de deformación en los sólidos. En la literatura se pueden encontrar varias definiciones de deformación equivalente. Una definición que se usa comúnmente en la literatura sobre plasticidad es

{displaystyle varepsilon _{mathrm {eq} }={sqrt {{tfrac {2}{3}}{boldsymbol {varepsilon }}^{mathrm {dev} }:{boldsymbol {varepsilon }}^{mathrm {dev} }}}={sqrt {{tfrac {2}{3}}varepsilon _{ij}^{mathrm {dev} }varepsilon _{ij}^{mathrm {dev} }}}~;~~{boldsymbol {varepsilon }}^{mathrm {dev} }={boldsymbol {varepsilon }}-{tfrac {1}{3}}mathrm {tr} ({boldsymbol {varepsilon }})~{boldsymbol {I}}}

{displaystyle sigma _{mathrm {eq} }={sqrt {{tfrac {3}{2}}{boldsymbol {sigma }}^{mathrm {dev} }:{boldsymbol {sigma }}^{mathrm {dev} }}}}

Ecuaciones de compatibilidad

Para componentes de tensión prescritos $varepsilon _{ij}$ la ecuación tensor de tensión ${displaystyle u_{i,j}+u_{j,i}=2varepsilon _{ij}}$ representa un sistema de seis ecuaciones diferenciales para la determinación de tres componentes de desplazamiento $u_{i}$ , dando un sistema demasiado determinado. Por lo tanto, una solución no existe generalmente para una elección arbitraria de componentes de tensión. Por lo tanto, algunas restricciones, llamadas ecuaciones de compatibilidad, se imponen sobre los componentes de la cepa. Con la adición de las tres ecuaciones de compatibilidad el número de ecuaciones independientes se reduce a tres, coincidiendo con el número de componentes desconocidos de desplazamiento. Estas limitaciones en el tensor de cepa fueron descubiertas por Saint-Venant, y se llaman las "ecuaciones de compatibilidad con SAINT Venant".

Las funciones de compatibilidad sirven para asegurar una función de desplazamiento continuo de valor único $u_{i}$ . Si el médium elástico se visualiza como un conjunto de cubos infinitesimal en el estado no entrenado, después de que el médium es tenso, un tensor de cepa arbitraria puede no producir una situación en la que los cubos distorsionados todavía encajan sin superposición.

En notación de índice, las ecuaciones de compatibilidad se expresan como

{displaystyle varepsilon _{ij,km}+varepsilon _{km,ij}-varepsilon _{ik,jm}-varepsilon _{jm,ik}=0}

En notación de ingeniería,

${displaystyle {frac {partial ^{2}epsilon _{x}}{partial y^{2}}}+{frac {partial ^{2}epsilon _{y}}{partial x^{2}}}=2{frac {partial ^{2}epsilon _{xy}}{partial xpartial y}}}$
${displaystyle {frac {partial ^{2}epsilon _{y}}{partial z^{2}}}+{frac {partial ^{2}epsilon _{z}}{partial y^{2}}}=2{frac {partial ^{2}epsilon _{yz}}{partial ypartial z}}}$
${displaystyle {frac {partial ^{2}epsilon _{x}}{partial z^{2}}}+{frac {partial ^{2}epsilon _{z}}{partial x^{2}}}=2{frac {partial ^{2}epsilon _{zx}}{partial zpartial x}}}$
${displaystyle {frac {partial ^{2}epsilon _{x}}{partial ypartial z}}={frac {partial }{partial x}}left(-{frac {partial epsilon _{yz}}{partial x}}+{frac {partial epsilon _{zx}}{partial y}}+{frac {partial epsilon _{xy}}{partial z}}right)}$
${displaystyle {frac {partial ^{2}epsilon _{y}}{partial zpartial x}}={frac {partial }{partial y}}left({frac {partial epsilon _{yz}}{partial x}}-{frac {partial epsilon _{zx}}{partial y}}+{frac {partial epsilon _{xy}}{partial z}}right)}$
${displaystyle {frac {partial ^{2}epsilon _{z}}{partial xpartial y}}={frac {partial }{partial z}}left({frac {partial epsilon _{yz}}{partial x}}+{frac {partial epsilon _{zx}}{partial y}}-{frac {partial epsilon _{xy}}{partial z}}right)}$

Casos especiales

Deformación plana

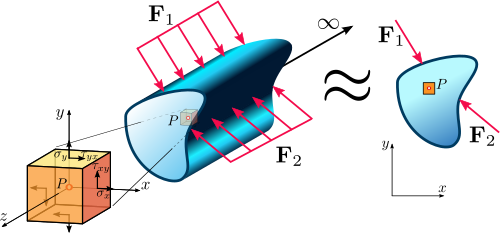
El estado de cepa plana en un continuum.

En componentes de ingeniería real, el estrés (y la cepa) son tensores 3-D pero en estructuras prismáticas como una cartilla de metal largo, la longitud de la estructura es mucho mayor que las otras dos dimensiones. Las cepas asociadas con la longitud, es decir, la cepa normal ${displaystyle varepsilon _{33}}$ y las cepas del tirón ${displaystyle varepsilon _{13}}$ y ${displaystyle varepsilon _{23}}$ (si la longitud es la 3-dirección) se limitan por material cercano y son pequeños en comparación con el cepas transversales. La cepa plana es entonces una aproximación aceptable. El tensor de tensión para la cepa plana está escrito como:

{displaystyle {underline {underline {boldsymbol {varepsilon }}}}={begin{bmatrix}varepsilon _{11}&varepsilon _{12}&0\varepsilon _{21}&varepsilon _{22}&0\0&0&0end{bmatrix}}}

tensión de avión

{displaystyle {underline {underline {boldsymbol {sigma }}}}={begin{bmatrix}sigma _{11}&sigma _{12}&0\sigma _{21}&sigma _{22}&0\0&0&sigma _{33}end{bmatrix}}}

sigma_{33}

{displaystyle epsilon _{33}=0}

Esfuerzo antiplano

La tensión antiplana es otro estado especial de tensión que puede ocurrir en un cuerpo, por ejemplo, en una región cercana a una dislocación de tornillo. El tensor de deformación para la deformación antiplana está dado por

{displaystyle {underline {underline {boldsymbol {varepsilon }}}}={begin{bmatrix}0&0&varepsilon _{13}\0&0&varepsilon _{23}\varepsilon _{13}&varepsilon _{23}&0end{bmatrix}}}

Tensor de rotación infinitesimal

El tensor de tensión infinitesimal se define como

{displaystyle {boldsymbol {varepsilon }}={frac {1}{2}}[{boldsymbol {nabla }}mathbf {u} +({boldsymbol {nabla }}mathbf {u})^{T}]}

{displaystyle {boldsymbol {nabla }}mathbf {u} ={boldsymbol {varepsilon }}+{boldsymbol {omega }}}

{displaystyle {boldsymbol {omega }}:={frac {1}{2}}[{boldsymbol {nabla }}mathbf {u} -({boldsymbol {nabla }}mathbf {u})^{T}]}

{boldsymbol {omega }}

Tensor de rotación infinitesimal

{boldsymbol {omega }}

|omega _{{ij}}|ll 1

ambos

El vector axial

Un tensor simétrico simétrico de segunda orden tiene tres componentes de escalar independientes. Estos tres componentes se utilizan para definir un vector axial, $mathbf {w}$ , como sigue

{displaystyle omega _{ij}=-epsilon _{ijk}~w_{k}~;~~w_{i}=-{tfrac {1}{2}}~epsilon _{ijk}~omega _{jk}}

epsilon _{ijk}

{displaystyle {underline {underline {boldsymbol {omega }}}}={begin{bmatrix}0&-w_{3}&w_{2}\w_{3}&0&-w_{1}\-w_{2}&w_{1}&0end{bmatrix}}~;~~{underline {mathbf {w} }}={begin{bmatrix}w_{1}\w_{2}\w_{3}end{bmatrix}}}

vector de rotación infinitesimal

{displaystyle mathbf {w} ={tfrac {1}{2}}~{boldsymbol {nabla }}times mathbf {u} }

{displaystyle w_{i}={tfrac {1}{2}}~epsilon _{ijk}~u_{k,j}}

lVert {boldsymbol {omega }}rVert ll 1

{boldsymbol {varepsilon }}={boldsymbol {0}}

|{mathbf {w}}|

mathbf {w}

Relación entre el tensor de deformación y el vector de rotación

Dado un campo de desplazamiento continuo y de valor único $mathbf {u}$ y el tensor de cepa infinitesimal correspondiente $boldsymbol{varepsilon}$ , tenemos (ver derivado Tensor (mecánica continua))

{displaystyle {boldsymbol {nabla }}times {boldsymbol {varepsilon }}=e_{ijk}~varepsilon _{lj,i}~mathbf {e} _{k}otimes mathbf {e} _{l}={tfrac {1}{2}}~e_{ijk}~[u_{l,ji}+u_{j,li}]~mathbf {e} _{k}otimes mathbf {e} _{l}}

{displaystyle u_{l,ji}=u_{l,ij}}

{displaystyle e_{ijk}u_{l,ji}=(e_{12k}+e_{21k})u_{l,12}+(e_{13k}+e_{31k})u_{l,13}+(e_{23k}+e_{32k})u_{l,32}=0}

{displaystyle {tfrac {1}{2}}~e_{ijk}~u_{j,li}=left({tfrac {1}{2}}~e_{ijk}~u_{j,i}right)_{,l}=left({tfrac {1}{2}}~e_{kij}~u_{j,i}right)_{,l}=w_{k,l}}

{displaystyle {boldsymbol {nabla }}times {boldsymbol {varepsilon }}=w_{k,l}~mathbf {e} _{k}otimes mathbf {e} _{l}={boldsymbol {nabla }}mathbf {w} }

Relación entre el tensor de rotación y el vector de rotación

De una identidad importante en relación con el rizo de un tensor sabemos que para un campo de desplazamiento continuo de valor único $mathbf {u}$ ,

{displaystyle {boldsymbol {nabla }}times ({boldsymbol {nabla }}mathbf {u})={boldsymbol {0}}.}

{boldsymbol {nabla }}{mathbf {u}}={boldsymbol {varepsilon }}+{boldsymbol {omega }}

{displaystyle {boldsymbol {nabla }}times {boldsymbol {omega }}=-{boldsymbol {nabla }}times {boldsymbol {varepsilon }}=-{boldsymbol {nabla }}mathbf {w}.}

Tensor de deformación en coordenadas cilíndricas

En coordenadas polares cilíndricas ( $r, theta, z$ ), el vector de desplazamiento se puede escribir como

{displaystyle mathbf {u} =u_{r}~mathbf {e} _{r}+u_{theta }~mathbf {e} _{theta }+u_{z}~mathbf {e} _{z}}

{displaystyle {begin{aligned}varepsilon _{rr}&={cfrac {partial u_{r}}{partial r}}\varepsilon _{theta theta }&={cfrac {1}{r}}left({cfrac {partial u_{theta }}{partial theta }}+u_{r}right)\varepsilon _{zz}&={cfrac {partial u_{z}}{partial z}}\varepsilon _{rtheta }&={cfrac {1}{2}}left({cfrac {1}{r}}{cfrac {partial u_{r}}{partial theta }}+{cfrac {partial u_{theta }}{partial r}}-{cfrac {u_{theta }}{r}}right)\varepsilon _{theta z}&={cfrac {1}{2}}left({cfrac {partial u_{theta }}{partial z}}+{cfrac {1}{r}}{cfrac {partial u_{z}}{partial theta }}right)\varepsilon _{zr}&={cfrac {1}{2}}left({cfrac {partial u_{r}}{partial z}}+{cfrac {partial u_{z}}{partial r}}right)end{aligned}}}

Tensor de deformación en coordenadas esféricas

En coordenadas esféricas ( $r,thetaphi$ ), el vector de desplazamiento se puede escribir como

Coordenadas esféricas (r, Silencio, φ) como se utiliza comúnmente en física: distancia radial r, ángulo polar Silencio (theta), y ángulo azimutal φ (phi). El símbolo *** (rho) se utiliza a menudo en lugar de r.

{displaystyle mathbf {u} =u_{r}~mathbf {e} _{r}+u_{theta }~mathbf {e} _{theta }+u_{phi }~mathbf {e} _{phi }}

{displaystyle {begin{aligned}varepsilon _{rr}&={cfrac {partial u_{r}}{partial r}}\varepsilon _{theta theta }&={cfrac {1}{r}}left({cfrac {partial u_{theta }}{partial theta }}+u_{r}right)\varepsilon _{phi phi }&={cfrac {1}{rsin theta }}left({cfrac {partial u_{phi }}{partial phi }}+u_{r}sin theta +u_{theta }cos theta right)\varepsilon _{rtheta }&={cfrac {1}{2}}left({cfrac {1}{r}}{cfrac {partial u_{r}}{partial theta }}+{cfrac {partial u_{theta }}{partial r}}-{cfrac {u_{theta }}{r}}right)\varepsilon _{theta phi }&={cfrac {1}{2r}}left({cfrac {1}{sin theta }}{cfrac {partial u_{theta }}{partial phi }}+{cfrac {partial u_{phi }}{partial theta }}-u_{phi }cot theta right)\varepsilon _{phi r}&={cfrac {1}{2}}left({cfrac {1}{rsin theta }}{cfrac {partial u_{r}}{partial phi }}+{cfrac {partial u_{phi }}{partial r}}-{cfrac {u_{phi }}{r}}right)end{aligned}}}

Contenido relacionado

Más resultados...