Teoría de juego
Teoría de juegos es el estudio de modelos matemáticos de interacciones estratégicas entre agentes racionales. Tiene aplicaciones en todos los campos de las ciencias sociales, así como en la lógica, la ciencia de sistemas y la informática. Originalmente, se refería a juegos de suma cero de dos personas, en los que las ganancias o pérdidas de cada participante se equilibran exactamente con las de los demás participantes. En el siglo XXI, la teoría de juegos se aplica a una amplia gama de relaciones de comportamiento; ahora es un término general para la ciencia de la toma de decisiones lógicas en humanos, animales y computadoras.
La teoría de juegos moderna comenzó con la idea de equilibrios de estrategias mixtas en juegos de suma cero de dos personas y su demostración por John von Neumann. La prueba original de Von Neumann usó el teorema del punto fijo de Brouwer sobre asignaciones continuas en conjuntos convexos compactos, que se convirtió en un método estándar en la teoría de juegos y la economía matemática. Su artículo fue seguido por el libro de 1944 Teoría de juegos y comportamiento económico, coescrito con Oskar Morgenstern, que consideraba juegos cooperativos de varios jugadores. La segunda edición de este libro proporcionó una teoría axiomática de la utilidad esperada, que permitió a los estadísticos y economistas matemáticos tratar la toma de decisiones bajo incertidumbre.
La teoría de juegos fue desarrollada ampliamente en la década de 1950 por muchos académicos. Se aplicó explícitamente a la evolución en la década de 1970, aunque desarrollos similares se remontan al menos a la década de 1930. La teoría de juegos ha sido ampliamente reconocida como una herramienta importante en muchos campos. A partir de 2020, con el Premio Nobel de Ciencias Económicas para los teóricos de juegos Paul Milgrom y Robert B. Wilson, quince teóricos de juegos han ganado el Premio Nobel de economía. John Maynard Smith recibió el Premio Crafoord por su aplicación de la teoría de juegos evolutiva.
Historia
Precursores
Los debates sobre las matemáticas de los juegos comenzaron mucho antes del surgimiento de la moderna teoría matemática de los juegos. El trabajo de Cardano sobre los juegos de azar en Liber de ludo aleae (Libro sobre los juegos de azar), que fue escrito alrededor de 1564 pero publicado póstumamente en 1663, formuló algunos de las ideas básicas del campo. En la década de 1650, Pascal y Huygens desarrollaron el concepto de expectativa en el razonamiento sobre la estructura de los juegos de azar, y Huygens publicó su cálculo de apuestas en De ratiociniis in ludo aleæ (Sobre el razonamiento en juegos de azar). Oportunidad) en 1657.
En 1713, una carta atribuida a Charles Waldegrave analizó un juego llamado "le Her". Era un jacobita activo y tío de James Waldegrave, un diplomático británico. En esta carta, Waldegrave proporcionó una solución de estrategia mixta minimax a una versión para dos personas del juego de cartas le Her, y el problema ahora se conoce como problema de Waldegrave. En sus Recherches sur les principes mathématiques de la théorie des richesses (Investigaciones sobre los principios matemáticos de la teoría de la riqueza) de 1838, Antoine Augustin Cournot consideró un duopolio y presentó una solución ese es el equilibrio de Nash del juego.
En 1913, Ernst Zermelo publicó Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels (Sobre una aplicación de la teoría de conjuntos a la teoría del juego de ajedrez), lo que demostró que la estrategia de ajedrez óptima está estrictamente determinada. Esto allanó el camino para teoremas más generales.
En 1938, el economista matemático danés Frederik Zeuthen demostró que el modelo matemático tenía una estrategia ganadora mediante el uso del teorema del punto fijo de Brouwer. En su libro de 1938 Applications aux Jeux de Hasard y notas anteriores, Émile Borel demostró un teorema minimax para juegos de matriz de suma cero de dos personas solo cuando la matriz de pagos es simétrica y proporciona una solución a un juego infinito no trivial (conocido en inglés como Blotto game). Borel conjeturó la inexistencia de equilibrios de estrategias mixtas en juegos finitos de suma cero de dos personas, una conjetura que von Neumann demostró que era falsa.
Nacimiento y desarrollo temprano
La teoría de juegos no existía como campo exclusivo hasta que John von Neumann publicó el artículo Sobre la teoría de los juegos de estrategia en 1928. La prueba original de Von Neumann utilizó la de Brouwer teorema del punto fijo sobre asignaciones continuas en conjuntos convexos compactos, que se convirtió en un método estándar en teoría de juegos y economía matemática. Su artículo fue seguido por su libro de 1944 Teoría de juegos y comportamiento económico en coautoría con Oskar Morgenstern. La segunda edición de este libro proporcionó una teoría axiomática de la utilidad, que reencarnó la antigua teoría de la utilidad (del dinero) de Daniel Bernoulli como una disciplina independiente. El trabajo de Von Neumann en teoría de juegos culminó en este libro de 1944. Este trabajo fundamental contiene el método para encontrar soluciones mutuamente consistentes para juegos de suma cero de dos personas. El trabajo posterior se centró principalmente en la teoría de juegos cooperativos, que analiza las estrategias óptimas para grupos de individuos, asumiendo que pueden hacer cumplir los acuerdos entre ellos sobre las estrategias adecuadas.
En 1950, apareció la primera discusión matemática sobre el dilema del prisionero, y los destacados matemáticos Merrill M. Flood y Melvin Dresher llevaron a cabo un experimento como parte de las investigaciones de RAND Corporation sobre la teoría de juegos.. RAND prosiguió los estudios debido a las posibles aplicaciones a la estrategia nuclear global. Casi al mismo tiempo, John Nash desarrolló un criterio para la consistencia mutua de los jugadores. estrategias conocidas como equilibrio de Nash, aplicable a una variedad de juegos más amplia que el criterio propuesto por von Neumann y Morgenstern. Nash demostró que cada juego no cooperativo finito de n jugadores, de suma no cero (no solo de dos jugadores de suma cero) tiene lo que ahora se conoce como un equilibrio de Nash en estrategias mixtas.
La teoría de juegos experimentó una gran actividad en la década de 1950, durante la cual se desarrollaron los conceptos del núcleo, el juego de forma extensiva, el juego ficticio, los juegos repetidos y el valor de Shapley. La década de 1950 también vio las primeras aplicaciones de la teoría de juegos a la filosofía y la ciencia política.
Logros premiados
En 1965, Reinhard Selten introdujo su concepto de solución de equilibrios perfectos en subjuegos, que perfeccionó aún más el equilibrio de Nash. Más tarde también introduciría la perfección de la mano temblorosa. En 1994, Nash, Selten y Harsanyi se convirtieron en Premios Nobel de Economía por sus contribuciones a la teoría económica de los juegos.
En la década de 1970, la teoría de juegos se aplicó ampliamente en biología, en gran parte como resultado del trabajo de John Maynard Smith y su estrategia evolutivamente estable. Además, se introdujeron y analizaron los conceptos de equilibrio correlacionado, perfección de mano temblorosa y conocimiento común.
En 2005, los teóricos de juegos Thomas Schelling y Robert Aumann siguieron a Nash, Selten y Harsanyi como premios Nobel. Schelling trabajó en modelos dinámicos, ejemplos tempranos de teoría de juegos evolutiva. Aumann contribuyó más a la escuela del equilibrio, introduciendo el engrosamiento del equilibrio y los equilibrios correlacionados, y desarrollando un extenso análisis formal del supuesto de conocimiento común y de sus consecuencias.
En 2007, Leonid Hurwicz, Eric Maskin y Roger Myerson recibieron el Premio Nobel de Economía "por haber sentado las bases de la teoría del diseño de mecanismos". Las contribuciones de Myerson incluyen la noción de equilibrio adecuado y un importante texto de posgrado: Teoría de juegos, análisis de conflictos. Hurwicz introdujo y formalizó el concepto de compatibilidad de incentivos.
En 2012, Alvin E. Roth y Lloyd S. Shapley recibieron el Premio Nobel de Economía "por la teoría de las asignaciones estables y la práctica del diseño de mercado". En 2014, el Nobel fue para el teórico de juegos Jean Tirole.
Tipos de juegos
Cooperativo / no cooperativo
Un juego es cooperativo si los jugadores pueden formar compromisos vinculantes exigidos externamente (por ejemplo, a través de la ley contractual). Un juego es no cooperativo si los jugadores no pueden formar alianzas o si todos los acuerdos deben cumplirse por sí mismos (por ejemplo, a través de amenazas creíbles).
Los juegos cooperativos a menudo se analizan a través del marco de la teoría del juego cooperativo, que se enfoca en predecir qué coaliciones se formarán, las acciones conjuntas que toman los grupos y los beneficios colectivos resultantes. Se opone a la tradicional teoría del juego no cooperativo que se centra en predecir jugadores individuales' acciones y pagos y análisis de equilibrios de Nash. El enfoque en la recompensa individual puede resultar en un fenómeno conocido como Tragedia de los Comunes, donde los recursos se utilizan a un nivel colectivo ineficiente. La falta de negociación formal conduce al deterioro de los bienes públicos por el uso excesivo y la provisión insuficiente que se deriva de los incentivos privados.
La teoría del juego cooperativo proporciona un enfoque de alto nivel, ya que describe solo la estructura, las estrategias y los pagos de las coaliciones, mientras que la teoría del juego no cooperativo también analiza cómo los procedimientos de negociación afectarán la distribución de los pagos dentro de cada coalición. Dado que la teoría de los juegos no cooperativos es más general, los juegos cooperativos pueden analizarse mediante el enfoque de la teoría de los juegos no cooperativos (lo contrario no es válido) siempre que se hagan suposiciones suficientes para abarcar todas las posibles estrategias disponibles para los jugadores debido a la posibilidad. de ejecución externa de la cooperación. Si bien puede ser deseable usar una sola teoría, en muchos casos no hay suficiente información disponible para modelar con precisión los procedimientos formales disponibles durante el proceso de negociación estratégica, o el modelo resultante sería demasiado complejo para ofrecer una herramienta práctica en el mundo real. En tales casos, la teoría del juego cooperativo proporciona un enfoque simplificado que permite el análisis del juego en general sin tener que hacer ninguna suposición sobre los poderes de negociación.
Simétrica / asimétrica
| E | F | |
| E | 1, 2 | 0, 0 |
| F | 0, 0 | 1, 2 |
| Un juego asimétrico | ||
Un juego simétrico es un juego en el que los beneficios de jugar una estrategia en particular dependen solo de las otras estrategias empleadas, no de quién las está jugando. Es decir, si las identidades de los jugadores se pueden cambiar sin cambiar el pago de las estrategias, entonces el juego es simétrico. Muchos de los juegos 2×2 comúnmente estudiados son simétricos. Las representaciones estándar del pollo, el dilema del prisionero y la caza del ciervo son todos juegos simétricos. Algunos estudiosos también considerarían ciertos juegos asimétricos como ejemplos de estos juegos. Sin embargo, los pagos más comunes para cada uno de estos juegos son simétricos.
Los juegos asimétricos más comúnmente estudiados son juegos en los que no hay conjuntos de estrategias idénticos para ambos jugadores. Por ejemplo, el juego del ultimátum y, de manera similar, el juego del dictador tienen diferentes estrategias para cada jugador. Sin embargo, es posible que un juego tenga estrategias idénticas para ambos jugadores y, sin embargo, sea asimétrico. Por ejemplo, el juego que se muestra en el gráfico de esta sección es asimétrico a pesar de tener conjuntos de estrategias idénticos para ambos jugadores.
Suma cero / suma distinta de cero
| A | B | |
| A | -1, 1 | 3 – 3 |
| B | 0, 0 | -2, 2 |
| Una suma cero juego | ||
Los juegos de suma cero (más generalmente, juegos de suma constante) son juegos en los que las elecciones de los jugadores no pueden aumentar ni disminuir los recursos disponibles. En los juegos de suma cero, el beneficio total va a todos los jugadores en un juego, para cada combinación de estrategias, siempre suma cero (más informalmente, un jugador se beneficia solo a expensas iguales de los demás). El póquer ejemplifica un juego de suma cero (ignorando la posibilidad de que la casa corte), porque uno gana exactamente la cantidad que pierden sus oponentes. Otros juegos de suma cero incluyen la combinación de centavos y la mayoría de los juegos de mesa clásicos, incluidos el Go y el ajedrez.
Muchos juegos estudiados por teóricos de juegos (incluido el famoso dilema del prisionero) son juegos de suma distinta de cero, porque el resultado tiene resultados netos mayores o menores que cero. De manera informal, en los juegos de suma distinta de cero, la ganancia de un jugador no se corresponde necesariamente con la pérdida de otro.
Los juegos de suma constante corresponden a actividades como el robo y el juego, pero no a la situación económica fundamental en la que existen ganancias potenciales del comercio. Es posible transformar cualquier juego de suma constante en un juego de suma cero (posiblemente asimétrico) agregando un jugador ficticio (a menudo llamado 'el tablero') cuyas pérdidas compensan las pérdidas de los jugadores. ganancias netas
Simultáneo/secuencial
Los juegos simultáneos son juegos en los que ambos jugadores se mueven simultáneamente o, en cambio, los últimos jugadores no se dan cuenta de que los primeros jugadores & # 39; acciones (haciéndolas efectivamente simultáneas). Los juegos secuenciales (o juegos dinámicos) son juegos en los que los jugadores posteriores tienen algún conocimiento sobre acciones anteriores. No es necesario que sea información perfecta sobre cada acción de los jugadores anteriores; puede ser muy poco conocimiento. Por ejemplo, un jugador puede saber que un jugador anterior no realizó una acción en particular, mientras que no sabe cuál de las otras acciones disponibles realizó realmente el primer jugador.
La diferencia entre juegos simultáneos y secuenciales se captura en las diferentes representaciones discutidas anteriormente. A menudo, la forma normal se usa para representar juegos simultáneos, mientras que la forma extensiva se usa para representar juegos secuenciales. La transformación de forma extensiva a normal es una forma, lo que significa que múltiples juegos en forma extensiva corresponden a la misma forma normal. En consecuencia, las nociones de equilibrio para juegos simultáneos son insuficientes para razonar sobre juegos secuenciales; ver perfección en subjuegos.
En resumen, las diferencias entre juegos secuenciales y simultáneos son las siguientes:
| Secuencial | Simultaneo | |
|---|---|---|
| Normalmente denotado por | Árboles de decisión | Matricidades de pago |
Conocimientos anteriores ¿de la jugada del oponente? | Sí. | No |
| ¿Eje del tiempo? | Sí. | No |
| También conocido como | Juegos Extensivo-form juego Juegos Extensivo juego | Estrategia juego Juego estratégico |
Competición de la Corte
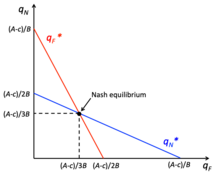
El modelo de competencia de Cournot implica que los jugadores elijan la cantidad de un producto homogéneo para producir de forma independiente y simultánea, donde el costo marginal puede ser diferente para cada empresa y el pago de la empresa es la ganancia. Los costos de producción son información pública y la empresa tiene como objetivo encontrar la cantidad que maximiza las ganancias en función de lo que creen que la otra empresa producirá y se comportará como monopolios. En este juego, las empresas quieren producir en la cantidad de monopolio, pero hay un gran incentivo para desviarse y producir más, lo que reduce el precio de equilibrio del mercado. Por ejemplo, las empresas pueden verse tentadas a desviarse de la cantidad de monopolio si hay una cantidad de monopolio baja y un precio alto, con el objetivo de aumentar la producción para maximizar las ganancias. Sin embargo, esta opción no proporciona la rentabilidad más alta, ya que la capacidad de una empresa para maximizar los beneficios depende de su cuota de mercado y de la elasticidad de la demanda del mercado. El equilibrio de Cournot se alcanza cuando cada empresa opera en su función de reacción sin incentivos para desviarse, ya que tienen la mejor respuesta basada en la producción de las otras empresas. Dentro del juego, las empresas alcanzan el equilibrio de Nash cuando se alcanza el equilibrio de Cournot.
Concurso Bertrand
La competencia de Bertrand, asume productos homogéneos y un costo marginal constante y los jugadores eligen los precios. El equilibrio de la competencia de precios es donde el precio es igual a los costos marginales, suponiendo información completa sobre los competidores' costos Por lo tanto, las empresas tienen un incentivo para desviarse del equilibrio porque un producto homogéneo con un precio más bajo ganará toda la participación de mercado, lo que se conoce como ventaja de costos.
Información perfecta e información imperfecta
Un subconjunto importante de juegos secuenciales consiste en juegos de información perfecta. Un juego es de información perfecta si todos los jugadores, en cada movimiento del juego, conocen los movimientos realizados previamente por todos los demás jugadores. En realidad, esto se puede aplicar a empresas y consumidores que tienen información sobre el precio y la calidad de todos los bienes disponibles en un mercado. Un juego de información imperfecta se juega cuando los jugadores no conocen todos los movimientos que ya ha realizado el oponente, como un juego de movimientos simultáneos. La mayoría de los juegos estudiados en teoría de juegos son juegos de información imperfecta. Los ejemplos de juegos de información perfecta incluyen tic-tac-toe, damas, ajedrez y Go.
Muchos juegos de cartas son juegos de información imperfecta, como el póquer y el bridge. La información perfecta a menudo se confunde con la información completa, que es un concepto similar. La información completa requiere que cada jugador conozca las estrategias y los pagos disponibles para los otros jugadores, pero no necesariamente las acciones realizadas, mientras que la información perfecta es el conocimiento de todos los aspectos del juego y de los jugadores. Sin embargo, los juegos de información incompleta pueden reducirse a juegos de información imperfecta introduciendo "movimientos por naturaleza".
Juego bayesiano
Una de las suposiciones del equilibrio de Nash es que cada jugador tiene creencias correctas sobre las acciones de los otros jugadores. Sin embargo, existen muchas situaciones en la teoría de juegos en las que los participantes no comprenden completamente las características de sus oponentes. Los negociadores pueden no estar al tanto de la valoración que hace su oponente del objeto de negociación, las empresas pueden no estar al tanto de las funciones de costos de su oponente, los combatientes pueden no estar al tanto de las fortalezas de su oponente y los jurados pueden no estar al tanto de la interpretación de su colega de la evidencia en el juicio. En algunos casos, los participantes pueden conocer bien el carácter de su oponente, pero pueden no saber qué tan bien su oponente conoce su propio carácter.
Juego bayesiano significa un juego estratégico con información incompleta. Para un juego estratégico, los que toman las decisiones son los jugadores, y cada jugador tiene un grupo de acciones. Una parte central de la especificación de información imperfecta es el conjunto de estados. Cada estado describe completamente una colección de características relevantes para el jugador, como sus preferencias y detalles sobre ellas. Debe haber un estado para cada conjunto de características que algún jugador cree que puede existir.
Por ejemplo, cuando el Jugador 1 no está seguro de si el Jugador 2 preferiría salir con ella o alejarse de ella, mientras que el Jugador 2 entiende las preferencias del Jugador 1 como antes. Para ser específicos, supongamos que el Jugador 1 cree que el Jugador 2 quiere salir con ella con una probabilidad de 1/2 y alejarse de ella con una probabilidad de 1/2 (esta evaluación proviene probablemente de la experiencia del Jugador 1: ella se enfrenta a jugadores que quieren salir con ella la mitad del tiempo en tal caso y jugadores que quieren evitarla la mitad del tiempo). Debido a la probabilidad involucrada, el análisis de esta situación requiere comprender la preferencia del jugador por las tablas, aunque a las personas solo les interesa el equilibrio estratégico puro.
Juegos combinatorios
Los juegos en los que la dificultad de encontrar una estrategia óptima se deriva de la multiplicidad de movimientos posibles se denominan juegos combinatorios. Los ejemplos incluyen ajedrez y Go. Los juegos que involucran información imperfecta también pueden tener un fuerte carácter combinatorio, por ejemplo, el backgammon. No existe una teoría unificada que aborde los elementos combinatorios en los juegos. Sin embargo, existen herramientas matemáticas que pueden resolver algunos problemas particulares y responder algunas preguntas generales.
Los juegos de información perfecta se han estudiado en la teoría de juegos combinatorios, que ha desarrollado representaciones novedosas, p. números surrealistas, así como métodos de prueba combinatorios y algebraicos (ya veces no constructivos) para resolver juegos de ciertos tipos, incluyendo "loopy" juegos que pueden resultar en secuencias infinitamente largas de movimientos. Estos métodos abordan juegos con mayor complejidad combinatoria que los que normalmente se consideran en la teoría de juegos tradicional (o "económica"). Un juego típico que se ha resuelto de esta manera es Hex. Un campo de estudio relacionado, basado en la teoría de la complejidad computacional, es la complejidad del juego, que se ocupa de estimar la dificultad computacional para encontrar estrategias óptimas.
La investigación en inteligencia artificial ha abordado juegos de información perfectos e imperfectos que tienen estructuras combinatorias muy complejas (como el ajedrez, el go o el backgammon) para los que no se han encontrado estrategias óptimas demostrables. Las soluciones prácticas implican heurística computacional, como la poda alfa-beta o el uso de redes neuronales artificiales entrenadas mediante aprendizaje por refuerzo, que hacen que los juegos sean más manejables en la práctica informática.
Juegos infinitamente largos
Los juegos, tal como los estudian los economistas y los jugadores del mundo real, generalmente se terminan en un número finito de movimientos. Los matemáticos puros no están tan limitados, y los teóricos de conjuntos en particular estudian juegos que duran infinitos movimientos, y el ganador (u otro pago) no se conoce hasta después de que se completan todos esos movimientos.
Normalmente, el foco de atención no está tanto en la mejor manera de jugar un juego de este tipo, sino en si un jugador tiene una estrategia ganadora. (Se puede probar, usando el axioma de elección, que hay juegos, incluso con información perfecta y donde los únicos resultados son 'ganar' o 'perder' - para los cuales ninguno de los jugadores tiene una estrategia ganadora). La existencia de tales estrategias, para juegos inteligentemente diseñados, tiene consecuencias importantes en la teoría descriptiva de conjuntos.
Juegos discretos y continuos
Gran parte de la teoría de juegos se ocupa de juegos finitos y discretos que tienen un número finito de jugadores, movimientos, eventos, resultados, etc. Sin embargo, muchos conceptos se pueden ampliar. Los juegos continuos permiten a los jugadores elegir una estrategia de un conjunto de estrategias continuas. Por ejemplo, la competencia de Cournot generalmente se modela con los jugadores ' siendo estrategias cualquier cantidad no negativa, incluidas cantidades fraccionarias.
Juegos diferenciales
Los juegos diferenciales como la persecución continua y el juego de evasión son juegos continuos donde la evolución de los jugadores & # 39; variables de estado se rige por ecuaciones diferenciales. El problema de encontrar una estrategia óptima en un juego diferencial está estrechamente relacionado con la teoría del control óptimo. En particular, hay dos tipos de estrategias: las estrategias de bucle abierto se encuentran utilizando el principio máximo de Pontryagin, mientras que las estrategias de bucle cerrado se encuentran utilizando el método de programación dinámica de Bellman.
Un caso particular de juegos diferenciales son los juegos con horizonte temporal aleatorio. En tales juegos, el tiempo terminal es una variable aleatoria con una función de distribución de probabilidad dada. Por lo tanto, los jugadores maximizan la expectativa matemática de la función de costo. Se demostró que el problema de optimización modificado se puede reformular como un juego diferencial descontado en un intervalo de tiempo infinito.
Teoría de juegos evolutiva
La teoría de juegos evolutiva estudia a los jugadores que ajustan sus estrategias a lo largo del tiempo de acuerdo con reglas que no son necesariamente racionales o previsoras. En general, la evolución de las estrategias a lo largo del tiempo de acuerdo con dichas reglas se modela como una cadena de Markov con una variable de estado como el perfil de la estrategia actual o cómo se ha jugado el juego en el pasado reciente. Dichas reglas pueden incluir la imitación, la optimización o la supervivencia del más apto.
En biología, estos modelos pueden representar la evolución, en la que la descendencia adopta a sus padres' estrategias y los padres que juegan estrategias más exitosas (es decir, correspondientes a pagos más altos) tienen un mayor número de hijos. En las ciencias sociales, tales modelos típicamente representan ajustes estratégicos por parte de jugadores que juegan un juego muchas veces durante su vida y, consciente o inconscientemente, ocasionalmente ajustan sus estrategias.
Resultados estocásticos (y relación con otros campos)
Los problemas de decisión individual con resultados estocásticos a veces se consideran "juegos de un solo jugador". Pueden modelarse utilizando herramientas similares dentro de las disciplinas relacionadas de la teoría de la decisión, la investigación de operaciones y las áreas de inteligencia artificial, en particular la planificación de IA (con incertidumbre) y el sistema multiagente. Aunque estos campos pueden tener diferentes motivadores, las matemáticas involucradas son sustancialmente las mismas, p. utilizando procesos de decisión de Markov (MDP).
Los resultados estocásticos también se pueden modelar en términos de teoría de juegos agregando un jugador que actúa aleatoriamente y que hace "movimientos fortuitos" ("se mueve por naturaleza"). Este jugador normalmente no se considera un tercer jugador en lo que de otro modo es un juego de dos jugadores, sino que simplemente sirve para proporcionar una tirada de dados cuando el juego lo requiera.
Para algunos problemas, diferentes enfoques para modelar resultados estocásticos pueden llevar a diferentes soluciones. Por ejemplo, la diferencia de enfoque entre los MDP y la solución minimax es que esta última considera el peor de los casos sobre un conjunto de movimientos adversarios, en lugar de razonar con expectativas sobre estos movimientos dada una distribución de probabilidad fija. El enfoque minimax puede ser ventajoso cuando los modelos estocásticos de incertidumbre no están disponibles, pero también puede estar sobreestimando eventos extremadamente improbables (pero costosos), lo que influye drásticamente en la estrategia en tales escenarios si se supone que un adversario puede obligar a que suceda tal evento. (Consulte la teoría del cisne negro para obtener más información sobre este tipo de problema de modelado, particularmente en lo que se refiere a la predicción y limitación de pérdidas en la banca de inversión).
También se han estudiado modelos generales que incluyen todos los elementos de resultados estocásticos, adversarios y observabilidad parcial o ruidosa (de movimientos de otros jugadores). El "estándar de oro" se considera un juego estocástico parcialmente observable (POSG), pero pocos problemas realistas son computacionalmente factibles en la representación POSG.
Metajuegos
Son juegos cuyo juego es el desarrollo de las reglas de otro juego, el objetivo o sujeto. Los metajuegos buscan maximizar el valor de utilidad del conjunto de reglas desarrollado. La teoría de los metajuegos está relacionada con la teoría del diseño de mecanismos.
El término análisis de metajuegos también se utiliza para referirse a un enfoque práctico desarrollado por Nigel Howard, en el que una situación se enmarca como un juego estratégico en el que las partes interesadas intentan alcanzar sus objetivos por medio de las opciones disponibles para ellos. Los desarrollos posteriores han llevado a la formulación del análisis de confrontación.
Juegos de billar
Estos son juegos que prevalecen sobre todas las formas de sociedad. Los juegos de pooling son juegos repetidos con una tabla de pagos cambiante en general sobre un camino experimentado, y sus estrategias de equilibrio usualmente toman una forma de convención social evolutiva y convención económica. La teoría del juego de agrupación surge para reconocer formalmente la interacción entre la elección óptima en una jugada y la aparición de la próxima ruta de actualización de la tabla de pagos, identificar la existencia y solidez de la invariancia y predecir la varianza a lo largo del tiempo. La teoría se basa en la clasificación de transformación topológica de la actualización de la tabla de pagos a lo largo del tiempo para predecir la varianza y la invariancia, y también está dentro de la jurisdicción de la ley computacional de la optimización alcanzable para un sistema ordenado.
Teoría del juego del campo medio
La teoría del juego de campo medio es el estudio de la toma de decisiones estratégicas en poblaciones muy grandes de pequeños agentes que interactúan. Esta clase de problemas fue considerada en la literatura económica por Boyan Jovanovic y Robert W. Rosenthal, en la literatura de ingeniería por Peter E. Caines y por los matemáticos Pierre-Louis Lions y Jean-Michel Lasry.
Representación de juegos
Los juegos estudiados en la teoría de juegos son objetos matemáticos bien definidos. Para estar completamente definido, un juego debe especificar los siguientes elementos: los jugadores del juego, la información y las acciones disponibles para cada jugador en cada punto de decisión y los beneficios de cada resultado. (Eric Rasmusen se refiere a estos cuatro "elementos esenciales" con el acrónimo "PAPI"). Un teórico de juegos generalmente usa estos elementos, junto con un concepto de solución de su elección, para deducir un conjunto de estrategias de equilibrio para cada jugador de modo que, cuando se emplean estas estrategias, ningún jugador puede beneficiarse desviándose unilateralmente de su estrategia. Estas estrategias de equilibrio determinan un equilibrio para el juego: un estado estable en el que ocurre un resultado o un conjunto de resultados con probabilidad conocida.
La mayoría de los juegos cooperativos se presentan en la forma de función característica, mientras que las formas extensiva y normal se utilizan para definir los juegos no cooperativos.
Forma extensiva
La forma extensiva se puede utilizar para formalizar juegos con una secuencia temporal de movimientos. Los juegos aquí se juegan en los árboles (como se muestra aquí). Aquí cada vértice (o nodo) representa un punto de elección para un jugador. El jugador se especifica mediante un número enumerado por el vértice. Las líneas que salen del vértice representan una posible acción para ese jugador. Los pagos se especifican en la parte inferior del árbol. La forma extensiva se puede ver como una generalización de múltiples jugadores de un árbol de decisión. Para resolver cualquier juego en forma extensiva se debe utilizar la inducción hacia atrás. Implica trabajar hacia atrás en el árbol del juego para determinar qué haría un jugador racional en el último vértice del árbol, qué haría el jugador con el movimiento anterior dado que el jugador con el último movimiento es racional, y así sucesivamente hasta el primer se alcanza el vértice del árbol.
El juego que se muestra consta de dos jugadores. La forma en que está estructurado este juego en particular (es decir, con toma de decisiones secuencial e información perfecta), Jugador 1 "se mueve" primero eligiendo F o U (justo o injusto). El siguiente en la secuencia, Jugador 2, que ahora ha visto Jugador 1's mueve, elige jugar A o R. Una vez que el Jugador 2 ha hecho su elección, el juego se considera terminado y cada jugador obtiene su pago respectivo. Supongamos que Jugador 1 elige U y luego Jugador 2 elige A: Jugador 1 luego obtiene un pago de "ocho" (que en términos del mundo real se puede interpretar de muchas maneras, la más simple de las cuales es en términos de dinero, pero podría significar cosas como ocho días de vacaciones u ocho países conquistados o incluso ocho oportunidades más para jugar el mismo juego contra otros jugadores) y el Jugador 2 obtiene un pago de "dos".
La forma extensiva también puede capturar juegos de movimientos simultáneos y juegos con información imperfecta. Para representarlo, una línea de puntos conecta diferentes vértices para representarlos como parte del mismo conjunto de información (es decir, los jugadores no saben en qué punto están), o se dibuja una línea cerrada alrededor de ellos. (Ver ejemplo en la sección de información imperfecta).
Forma normal
| Jugador 2 eliges Izquierda | Jugador 2 eliges Bien. | |
| Player 1 eliges Arriba | 4, 3 | –1, –1 |
| Player 1 eligesAbajo | 0, 0 | 3, 4 |
| Forma normal o matriz de pago de un juego de 2 jugadores, 2 estrategias | ||
El juego normal (o de forma estratégica) suele estar representado por una matriz que muestra los jugadores, las estrategias y los pagos (vea el ejemplo a la derecha). De manera más general, se puede representar mediante cualquier función que asocie un pago para cada jugador con cada combinación posible de acciones. En el ejemplo adjunto hay dos jugadores; uno elige la fila y el otro elige la columna. Cada jugador tiene dos estrategias, que se especifican por el número de filas y el número de columnas. Los pagos se proporcionan en el interior. El primer número es el pago recibido por el jugador de la fila (Jugador 1 en nuestro ejemplo); el segundo es el pago para el jugador de la columna (Jugador 2 en nuestro ejemplo). Suponga que el Jugador 1 juega Arriba y que el Jugador 2 juega Izquierda. Luego, el jugador 1 obtiene un pago de 4 y el jugador 2 obtiene 3.
Cuando un juego se presenta en forma normal, se presume que cada jugador actúa simultáneamente o, al menos, sin conocer las acciones del otro. Si los jugadores tienen alguna información sobre las elecciones de otros jugadores, el juego generalmente se presenta en forma extensa.
Cada juego de forma extensiva tiene un juego de forma normal equivalente; sin embargo, la transformación a la forma normal puede resultar en una explosión exponencial en el tamaño de la representación, lo que la hace poco práctica desde el punto de vista computacional.
Forma de función característica
En los juegos que poseen una utilidad extraíble, no se otorgan recompensas separadas; más bien, la función característica decide el pago de cada unidad. La idea es que la unidad que está 'vacía', por así decirlo, no recibe recompensa alguna.
El origen de esta forma se encuentra en el libro de John von Neumann y Oskar Morgenstern; al mirar estas instancias, adivinaron que cuando un sindicato C{displaystyle mathbf {C} aparece, funciona contra la fracción ()NC){displaystyle left({frac {mathbf {N} {fn} {fnK}}right)}como si dos individuos estuvieran jugando un juego normal. El pago equilibrado de C es una función básica. Aunque hay ejemplos diferentes que ayudan a determinar las cantidades de coalición de los juegos normales, no todos aparecen que en su forma de función puede derivarse de tales.
Formally, una función característica se ve como: (N,v), donde N representa el grupo de personas y v:2N→ → R{displaystyle v:2^{N}to mathbf {R} es una utilidad normal.
Estas funciones características se han ampliado para describir juegos en los que no existe una utilidad extraíble.
Representaciones alternativas del juego
Se utilizan formas alternativas de representación de juegos para algunas subclases de juegos o se ajustan a las necesidades de la investigación interdisciplinaria. Además de las representaciones clásicas del juego, algunas de las representaciones alternativas también codifican aspectos relacionados con el tiempo.
| Nombre | Año | Significado | Tipo de juegos | Hora |
|---|---|---|---|---|
| Congestión juego | 1973 | funciones | subconjunto de juegos n-persona, movimientos simultáneos | No |
| Forma secuencial | 1994 | matrices | Juegos de 2 personas de información imperfecta | No |
| Juegos de tiempo | 1994 | funciones | Juegos de 2 personas | Sí. |
| Gala | 1997 | lógica | n-person juegos de información imperfecta | No |
| Juegos Gráficos | 2001 | gráficos, funciones | juegos n-persona, movimientos simultáneos | No |
| Juegos de efectos locales | 2003 | funciones | subconjunto de juegos n-persona, movimientos simultáneos | No |
| GDL | 2005 | lógica | determinista n-person juegos, movimientos simultáneos | No |
| Juego Petri-nets | 2006 | Petri net | determinista n-person juegos, movimientos simultáneos | No |
| Juegos continuos | 2007 | funciones | subconjunto de juegos de 2 personas de información imperfecta | Sí. |
| PNSI | 2008 | Petri net | n-person juegos de información imperfecta | Sí. |
| Gráfico de acción juegos | 2012 | gráficos, funciones | juegos n-persona, movimientos simultáneos | No |
Usos generales y aplicados
Como método de matemáticas aplicadas, la teoría de juegos se ha utilizado para estudiar una amplia variedad de comportamientos humanos y animales. Inicialmente se desarrolló en economía para comprender una gran colección de comportamientos económicos, incluidos los comportamientos de las empresas, los mercados y los consumidores. El primer uso del análisis de teoría de juegos fue por Antoine Augustin Cournot en 1838 con su solución del duopolio de Cournot. El uso de la teoría de juegos en las ciencias sociales se ha expandido y la teoría de juegos también se ha aplicado a comportamientos políticos, sociológicos y psicológicos.
Aunque los naturalistas anteriores al siglo XX, como Charles Darwin, hicieron afirmaciones del tipo de la teoría de juegos, el uso del análisis de la teoría de juegos en biología comenzó con los estudios de Ronald Fisher sobre el comportamiento animal durante la década de 1930. Este trabajo es anterior al nombre "teoría de juegos", pero comparte muchas características importantes con este campo. Los desarrollos en economía fueron posteriormente aplicados a la biología en gran parte por John Maynard Smith en su libro de 1982 Evolution and the Theory of Games.
Además de usarse para describir, predecir y explicar el comportamiento, la teoría de juegos también se ha utilizado para desarrollar teorías de comportamiento ético o normativo y para prescribir dicho comportamiento. En economía y filosofía, los académicos han aplicado la teoría de juegos para ayudar a comprender el comportamiento bueno o apropiado. Los argumentos de teoría de juegos de este tipo se pueden encontrar desde Platón. Una versión alternativa de la teoría de juegos, llamada teoría química de juegos, representa las elecciones del jugador como moléculas reactivas químicas metafóricas llamadas "knowlecules". La teoría de juegos químicos luego calcula los resultados como soluciones de equilibrio para un sistema de reacciones químicas.
Descripción y modelado
El uso principal de la teoría de juegos es describir y modelar cómo se comportan las poblaciones humanas. Algunos académicos creen que al encontrar los equilibrios de los juegos pueden predecir cómo se comportarán las poblaciones humanas reales cuando se enfrenten a situaciones análogas al juego que se está estudiando. Esta visión particular de la teoría de juegos ha sido criticada. Se argumenta que las suposiciones hechas por los teóricos de los juegos a menudo se violan cuando se aplican a situaciones del mundo real. Los teóricos de los juegos suelen suponer que los jugadores actúan de manera racional, pero en la práctica, el comportamiento humano a menudo se desvía de este modelo. Los teóricos de los juegos responden comparando sus supuestos con los que se utilizan en la física. Por lo tanto, si bien sus suposiciones no siempre se cumplen, pueden tratar la teoría de juegos como un ideal científico razonable similar a los modelos utilizados por los físicos. Sin embargo, el trabajo empírico ha demostrado que en algunos juegos clásicos, como el juego del ciempiés, adivina 2/3 del juego promedio y el juego del dictador, las personas normalmente no juegan equilibrios de Nash. Hay un debate en curso sobre la importancia de estos experimentos y si el análisis de los experimentos captura completamente todos los aspectos de la situación relevante.
Algunos teóricos de juegos, siguiendo el trabajo de John Maynard Smith y George R. Price, han recurrido a la teoría de juegos evolutiva para resolver estos problemas. Estos modelos suponen o no racionalidad o racionalidad limitada por parte de los jugadores. A pesar del nombre, la teoría de los juegos evolutivos no presupone necesariamente la selección natural en el sentido biológico. La teoría evolutiva del juego incluye tanto la evolución biológica como la cultural y también modelos de aprendizaje individual (por ejemplo, dinámicas de juego ficticias).
Análisis prescriptivo o normativo
| Cooperate | Defecto | |
| Cooperate | -1, -1 | -10, 0 |
| Defecto | 0, -10 | -5, -5 |
| El dilema del prisionero | ||
Algunos académicos ven la teoría de juegos no como una herramienta de predicción del comportamiento de los seres humanos, sino como una sugerencia de cómo deberían comportarse las personas. Dado que una estrategia, correspondiente a un equilibrio de Nash de un juego, constituye la mejor respuesta de uno a las acciones de los otros jugadores, siempre que estén en (el mismo) equilibrio de Nash, jugar una estrategia que es parte de un equilibrio de Nash parece adecuado. Este uso normativo de la teoría de juegos también ha sido criticado.
Economía y empresa
La teoría de juegos es un método importante utilizado en economía matemática y negocios para modelar comportamientos competitivos de agentes que interactúan. Las aplicaciones incluyen una amplia gama de fenómenos y enfoques económicos, como subastas, negociación, precios de fusiones y adquisiciones, división justa, duopolios, oligopolios, formación de redes sociales, economía computacional basada en agentes, equilibrio general, diseño de mecanismos y sistemas de votación; y en áreas tan amplias como la economía experimental, la economía del comportamiento, la economía de la información, la organización industrial y la economía política.
Esta investigación generalmente se enfoca en conjuntos particulares de estrategias conocidas como "conceptos de solución" o "equilibrios". Una suposición común es que los jugadores actúan racionalmente. En los juegos no cooperativos, el más famoso de ellos es el equilibrio de Nash. Un conjunto de estrategias es un equilibrio de Nash si cada una representa la mejor respuesta a las otras estrategias. Si todos los jugadores están jugando las estrategias en un equilibrio de Nash, no tienen ningún incentivo unilateral para desviarse, ya que su estrategia es la mejor que pueden hacer dado lo que otros están haciendo.
Los pagos del juego generalmente se toman para representar la utilidad de los jugadores individuales.
Un artículo prototípico sobre teoría de juegos en economía comienza presentando un juego que es una abstracción de una situación económica particular. Se eligen uno o más conceptos de solución y el autor demuestra qué conjuntos de estrategias en el juego presentado son equilibrios del tipo apropiado. Los economistas y profesores de negocios sugieren dos usos principales (mencionados anteriormente): descriptivo y prescriptivo.
El Instituto Colegiado de Adquisiciones & Supply (CIPS) promueve el conocimiento y uso de la teoría de juegos en el contexto de las compras comerciales. CIPS y TWS Partners han realizado una serie de encuestas diseñadas para explorar la comprensión, el conocimiento y la aplicación de la teoría de juegos entre los profesionales de adquisiciones. Algunos de los principales hallazgos de su tercera encuesta anual (2019) incluyen:
- la aplicación de la teoría del juego a la actividad de adquisición ha aumentado – en el momento era al 19% en todos los encuestados
- 65% de los participantes predicen que el uso de aplicaciones de la teoría del juego crecerá
- 70% de los encuestados dicen que tienen "sólo una comprensión básica o inferior a la teoría del juego"
- 20% de los participantes habían realizado entrenamiento en el trabajo en la teoría del juego
- 50% de los encuestados dijeron que las soluciones de software nuevas o mejoradas eran deseables
- El 90% de los encuestados dijeron que no tienen el software que necesitan para su trabajo.
Gestión de proyectos
La toma de decisiones sensata es fundamental para el éxito de los proyectos. En la gestión de proyectos, la teoría de juegos se utiliza para modelar el proceso de toma de decisiones de los participantes, como inversores, directores de proyectos, contratistas, subcontratistas, gobiernos y clientes. Muy a menudo, estos jugadores tienen intereses contrapuestos y, a veces, sus intereses son directamente perjudiciales para otros jugadores, lo que hace que los escenarios de gestión de proyectos sean adecuados para ser modelados por la teoría de juegos.
Piraveenan (2019) en su revisión proporciona varios ejemplos en los que se utiliza la teoría de juegos para modelar escenarios de gestión de proyectos. Por ejemplo, un inversionista generalmente tiene varias opciones de inversión, y cada opción probablemente dará como resultado un proyecto diferente y, por lo tanto, se debe elegir una de las opciones de inversión antes de que se pueda producir el acta de constitución del proyecto. De manera similar, cualquier proyecto grande que involucre a subcontratistas, por ejemplo, un proyecto de construcción, tiene una interacción compleja entre el contratista principal (el gerente del proyecto) y los subcontratistas, o entre los propios subcontratistas, que normalmente tiene varios puntos de decisión. Por ejemplo, si existe una ambigüedad en el contrato entre el contratista y el subcontratista, cada uno debe decidir cuánto presionar con su caso sin poner en peligro todo el proyecto y, por lo tanto, su propio interés en él. De manera similar, cuando se lanzan proyectos de organizaciones competidoras, el personal de marketing tiene que decidir cuál es el mejor momento y estrategia para comercializar el proyecto, o su producto o servicio resultante, para que pueda ganar la máxima tracción frente a la competencia. En cada uno de estos escenarios, las decisiones requeridas dependen de las decisiones de otros jugadores que, de alguna manera, tienen intereses que compiten con los intereses del tomador de decisiones y, por lo tanto, idealmente se pueden modelar utilizando la teoría de juegos.
Piraveenan resume que los juegos de dos jugadores se utilizan predominantemente para modelar escenarios de gestión de proyectos y, en función de la identidad de estos jugadores, se utilizan cinco tipos distintos de juegos en la gestión de proyectos.
- Juegos del sector público-privado (juegos que modelan las alianzas entre el sector público y el privado)
- Juegos Contratista-contratista
- Juegos de contratistas-subcontratistas
- Subcontratista-subcontratista juegos
- Juegos con otros jugadores
En términos de tipos de juegos, tanto cooperativos como no cooperativos, tanto de forma normal como extensiva, y de suma cero y no cero, se utilizan para modelar varios escenarios de gestión de proyectos.
Ciencias políticas
La aplicación de la teoría de juegos a la ciencia política se centra en las áreas superpuestas de división justa, economía política, elección pública, negociación de guerra, teoría política positiva y teoría de la elección social. En cada una de estas áreas, los investigadores han desarrollado modelos de teoría de juegos en los que los jugadores suelen ser votantes, estados, grupos de intereses especiales y políticos.
Anthony Downs proporciona los primeros ejemplos de la teoría de juegos aplicada a la ciencia política. En su libro de 1957 Una teoría económica de la democracia, aplica el modelo de localización de empresas de Hotelling al proceso político. En el modelo downsiano, los candidatos políticos se comprometen con ideologías en un espacio político unidimensional. Downs primero muestra cómo los candidatos políticos convergerán hacia la ideología preferida por el votante medio si los votantes están completamente informados, pero luego argumenta que los votantes eligen permanecer racionalmente ignorantes, lo que permite la divergencia de candidatos. La teoría de juegos se aplicó en 1962 a la crisis de los misiles en Cuba durante la presidencia de John F. Kennedy.
También se ha propuesto que la teoría de juegos explica la estabilidad de cualquier forma de gobierno político. Tomando el caso más simple de una monarquía, por ejemplo, el rey, siendo una sola persona, no mantiene ni puede mantener su autoridad ejerciendo personalmente el control físico sobre todos o incluso sobre un número significativo de sus súbditos. En cambio, el control soberano se explica por el reconocimiento por parte de cada ciudadano de que todos los demás ciudadanos esperan ver al rey (u otro gobierno establecido) como la persona cuyas órdenes se seguirán. La comunicación coordinada entre los ciudadanos para reemplazar al soberano está efectivamente prohibida, ya que la conspiración para reemplazar al soberano generalmente se castiga como un delito. Así, en un proceso que puede ser modelado por variantes del dilema del prisionero, durante períodos de estabilidad ningún ciudadano encontrará racional moverse para reemplazar al soberano, incluso si todos los ciudadanos saben que estarían mejor si lo hicieran. todos debían actuar colectivamente.
Una explicación de la teoría del juego para la paz democrática es que el debate público y abierto en las democracias envía información clara y confiable sobre sus intenciones a otros estados. En contraste, es difícil saber las intenciones de los líderes no democráticos, qué efecto tendrán las concesiones y si se cumplirán las promesas. Por lo tanto, habrá desconfianza y falta de voluntad para hacer concesiones si al menos una de las partes en una disputa no es una democracia.
Sin embargo, la teoría de juegos predice que dos países aún pueden ir a la guerra incluso si sus líderes son conscientes de los costos de la guerra. La guerra puede resultar de información asimétrica; dos países pueden tener incentivos para tergiversar la cantidad de recursos militares que tienen a mano, haciéndolos incapaces de resolver disputas de manera agradable sin recurrir a la lucha. Además, la guerra puede surgir debido a problemas de compromiso: si dos países desean resolver una disputa por medios pacíficos, pero cada uno desea retractarse de los términos de ese acuerdo, es posible que no tengan más remedio que recurrir a la guerra. Finalmente, la guerra puede resultar de la indivisibilidad de los problemas.
La teoría de juegos también podría ayudar a predecir las respuestas de una nación cuando hay una nueva regla o ley que aplicar a esa nación. Un ejemplo es la investigación de Peter John Wood (2013) que investiga qué podrían hacer las naciones para ayudar a reducir el cambio climático. Wood pensó que esto podría lograrse firmando tratados con otras naciones para reducir las emisiones de gases de efecto invernadero. Sin embargo, concluyó que esta idea no podría funcionar porque crearía un dilema del prisionero para las naciones.
Biología
| Hawk | Dove | |
| Hawk | 20, 20 | 80, 40 |
| Dove | 40, 80 | 60, 60 |
| El halcón-dove juego | ||
A diferencia de los de economía, los beneficios de los juegos en biología a menudo se interpretan como correspondientes a la aptitud. Además, la atención se ha centrado menos en los equilibrios que corresponden a una noción de racionalidad y más en los que serían mantenidos por las fuerzas evolutivas. El equilibrio más conocido en biología se conoce como estrategia evolutivamente estable (ESS), introducido por primera vez en (Maynard Smith & Price 1973). Aunque su motivación inicial no implicaba ninguno de los requisitos mentales del equilibrio de Nash, todo ESS es un equilibrio de Nash.
En biología, la teoría de juegos se ha utilizado como modelo para comprender muchos fenómenos diferentes. Se utilizó por primera vez para explicar la evolución (y la estabilidad) de las proporciones sexuales aproximadas de 1:1. (Fisher 1930) harv error: no target: CITEREFFisher1930 (ayuda) sugirió que el sexo 1:1 Las proporciones son el resultado de fuerzas evolutivas que actúan sobre individuos que podrían verse como tratando de maximizar su número de nietos.
Además, los biólogos han utilizado la teoría de juegos evolutiva y la ESS para explicar el surgimiento de la comunicación animal. El análisis de los juegos de señalización y otros juegos de comunicación ha proporcionado información sobre la evolución de la comunicación entre animales. Por ejemplo, el comportamiento de mobbing de muchas especies, en el que un gran número de animales de presa atacan a un depredador más grande, parece ser un ejemplo de organización emergente espontánea. También se ha demostrado que las hormigas exhiben un comportamiento de avance similar a la moda (ver Butterfly Economics de Paul Ormerod).
Los biólogos han utilizado el juego del pollo para analizar el comportamiento de lucha y la territorialidad.
Según Maynard Smith, en el prefacio de Evolution and the Theory of Games, "paradójicamente, ha resultado que la teoría de juegos se aplica más fácilmente a la biología que al campo de la comportamiento económico para el que fue originalmente diseñado". La teoría de juegos evolutivos se ha utilizado para explicar muchos fenómenos aparentemente incongruentes en la naturaleza.
Uno de estos fenómenos se conoce como altruismo biológico. Esta es una situación en la que un organismo parece actuar de una manera que beneficia a otros organismos y es perjudicial para sí mismo. Esto es distinto de las nociones tradicionales de altruismo porque tales acciones no son conscientes, sino que parecen ser adaptaciones evolutivas para aumentar la aptitud general. Se pueden encontrar ejemplos en especies que van desde murciélagos vampiros que regurgitan la sangre que han obtenido de una caza nocturna y se la dan a los miembros del grupo que no se han podido alimentar, hasta abejas obreras que cuidan de la abeja reina durante toda su vida y nunca aparearse, a los monos verdes que advierten a los miembros del grupo sobre el acercamiento de un depredador, incluso cuando pone en peligro la posibilidad de supervivencia de ese individuo. Todas estas acciones aumentan la aptitud general de un grupo, pero tienen un costo para el individuo.
La teoría de los juegos evolutivos explica este altruismo con la idea de la selección de parentesco. Los altruistas discriminan entre las personas a las que ayudan y favorecen a los familiares. La regla de Hamilton explica la lógica evolutiva detrás de esta selección con la ecuación c < b × r, donde el costo c para el altruista debe ser menor que el beneficio b al destinatario multiplicado por el coeficiente de relación r. Los dos organismos más estrechamente relacionados hacen que aumente la incidencia de altruismo porque comparten muchos de los mismos alelos. Esto significa que el individuo altruista, al asegurarse de que los alelos de su pariente cercano se transmiten a través de la supervivencia de su descendencia, puede renunciar a la opción de tener descendencia porque se transmite la misma cantidad de alelos. Por ejemplo, ayudar a un hermano (en animales diploides) tiene un coeficiente de 1⁄ 2, porque (en promedio) un individuo comparte la mitad de los alelos en la descendencia de su hermano. Asegurar que suficiente descendencia de un hermano sobreviva hasta la edad adulta excluye la necesidad de que el individuo altruista produzca descendencia. Los valores de los coeficientes dependen en gran medida del alcance del campo de juego; por ejemplo, si la elección de a quién favorecer incluye todos los seres vivos genéticos, no solo todos los parientes, asumimos que la discrepancia entre todos los humanos solo representa aproximadamente el 1 % de la diversidad en el campo de juego, un coeficiente que era 1⁄2 en el campo más pequeño se convierte en 0,995. De manera similar, si se considera que la información distinta a la de naturaleza genética (por ejemplo, epigenética, religión, ciencia, etc.) persistió a lo largo del tiempo, el campo de juego se vuelve aún más grande y las discrepancias más pequeñas.
Informática y lógica
La teoría de juegos ha llegado a desempeñar un papel cada vez más importante en la lógica y la informática. Varias teorías lógicas tienen una base en la semántica del juego. Además, los informáticos han utilizado juegos para modelar cálculos interactivos. Además, la teoría de juegos proporciona una base teórica al campo de los sistemas multiagente.
Por otra parte, la teoría de juegos ha desempeñado un papel en los algoritmos en línea; en particular, el problema del servidor k, que en el pasado se ha denominado juegos con costos de movimiento y juegos de solicitud-respuesta. El principio de Yao es una técnica de teoría de juegos para demostrar los límites inferiores de la complejidad computacional de los algoritmos aleatorios, especialmente los algoritmos en línea.
La aparición de Internet ha motivado el desarrollo de algoritmos para encontrar equilibrios en juegos, mercados, subastas computacionales, sistemas peer-to-peer y mercados de seguridad e información. La teoría de juegos algorítmicos y dentro de ella el diseño de mecanismos algorítmicos combinan el diseño de algoritmos computacionales y el análisis de sistemas complejos con la teoría económica.
Filosofía
| Stag | Hare | |
| Stag | 3, 3 | 0, 2 |
| Hare | 2, 0 | 2, 2 |
| Caza de basura | ||
La teoría de juegos ha tenido varios usos en filosofía. En respuesta a dos artículos de W.V.O. Quine (1960, 1967), Lewis (1969) utilizaron la teoría de juegos para desarrollar una explicación filosófica de la convención. Al hacerlo, proporcionó el primer análisis del conocimiento común y lo empleó para analizar el juego en los juegos de coordinación. Además, primero sugirió que uno puede entender el significado en términos de juegos de señalización. Esta sugerencia posterior ha sido seguida por varios filósofos desde Lewis. Siguiendo la descripción de las convenciones de la teoría de juegos de Lewis (1969), Edna Ullmann-Margalit (1977) y Bicchieri (2006) han desarrollado teorías de normas sociales que las definen como equilibrios de Nash que resultan de transformar un juego de motivos mixtos en un juego de coordinación.
La teoría de juegos también ha desafiado a los filósofos a pensar en términos de epistemología interactiva: qué significa para un colectivo tener creencias o conocimientos comunes, y cuáles son las consecuencias de este conocimiento para los resultados sociales resultantes de las interacciones de los agentes. Los filósofos que han trabajado en esta área incluyen a Bicchieri (1989, 1993), Skyrms (1990) y Stalnaker (1999).
En ética, algunos autores (sobre todo David Gauthier, Gregory Kavka y Jean Hampton) han intentado perseguir a Thomas Hobbes' proyecto de derivar la moralidad del interés propio. Dado que juegos como el dilema del prisionero presentan un conflicto aparente entre la moralidad y el interés propio, explicar por qué el interés propio requiere la cooperación es un componente importante de este proyecto. Esta estrategia general es un componente de la visión general del contrato social en la filosofía política (para ejemplos, véase Gauthier (1986) y Kavka (1986) error de harvtxt: sin destino: CITEREFKavka1986 (ayuda)).
Otros autores han intentado utilizar la teoría evolutiva de juegos para explicar el surgimiento de actitudes humanas sobre la moralidad y los comportamientos animales correspondientes. Estos autores analizan varios juegos, incluidos el dilema del prisionero, la caza del ciervo y el juego de negociación de Nash, como una explicación del surgimiento de actitudes sobre la moralidad (ver, por ejemplo, Skyrms (1996, 2004) y Sober y Wilson (1998)).
Precios de productos de consumo y minoristas
Las aplicaciones de la teoría de juegos se utilizan a menudo en las estrategias de fijación de precios de los mercados minoristas y de consumo, especialmente para la venta de bienes inelásticos. Dado que los minoristas compiten constantemente entre sí por la cuota de mercado de los consumidores, se ha convertido en una práctica bastante común que los minoristas descuenten ciertos productos, de forma intermitente, con la esperanza de aumentar el tráfico peatonal en las ubicaciones físicas (visitas a sitios web para minoristas de comercio electrónico) o aumentar las ventas de productos auxiliares o complementarios.
El Black Friday, una festividad de compras popular en los EE. UU., es cuando muchos minoristas se enfocan en estrategias de precios óptimas para capturar el mercado de compras navideñas. En el escenario del Black Friday, los minoristas que usan aplicaciones de teoría de juegos generalmente preguntan "¿cuál es la reacción del competidor dominante hacia mí?" En tal escenario, el juego tiene dos jugadores: el minorista y el consumidor. El minorista se centra en una estrategia de precios óptima, mientras que el consumidor se centra en la mejor oferta. En este sistema cerrado, a menudo no existe una estrategia dominante ya que ambos jugadores tienen opciones alternativas. Es decir, los minoristas pueden encontrar un cliente diferente y los consumidores pueden comprar en un minorista diferente. Sin embargo, dada la competencia del mercado ese día, la estrategia dominante para los minoristas radica en superar a los competidores. El sistema abierto supone múltiples minoristas que venden productos similares y un número finito de consumidores que demandan los productos a un precio óptimo. Un blog de un profesor de la Universidad de Cornell brindó un ejemplo de tal estrategia, cuando Amazon fijó un precio de un televisor Samsung $ 100 por debajo del valor minorista, lo que efectivamente socavó a los competidores. Amazon compensó parte de la diferencia al aumentar el precio de los cables HDMI, ya que se descubrió que los consumidores discriminan menos los precios cuando se trata de la venta de artículos secundarios.
Los mercados minoristas continúan desarrollando estrategias y aplicaciones de la teoría de juegos en lo que respecta a la fijación de precios de bienes de consumo. Los conocimientos clave encontrados entre las simulaciones en un entorno controlado y las experiencias minoristas del mundo real muestran que las aplicaciones de tales estrategias son más complejas, ya que cada minorista debe encontrar un equilibrio óptimo entre los precios, las relaciones con los proveedores, la imagen de marca y el potencial de canibalizar. la venta de artículos más rentables.
Epidemiología
Dado que la decisión de recibir una vacuna para una enfermedad en particular a menudo la toman individuos, quienes pueden considerar una variedad de factores y parámetros al tomar esta decisión (como la incidencia y prevalencia de la enfermedad, los riesgos percibidos y reales asociados con contraer la enfermedad, la tasa de mortalidad, los riesgos percibidos y reales asociados con la vacunación y el costo financiero de la vacunación), la teoría de juegos se ha utilizado para modelar y predecir la aceptación de la vacunación en una sociedad.
En la cultura popular
- Basado en el libro de 1998 de Sylvia Nasar, la historia de vida del teórico del juego y matemático John Nash se convirtió en el biopic 2001 Una mente hermosa, protagonizando a Russell Crowe como Nash.
- La novela de ciencia ficción militar de 1959 Troopers de Starship por Robert A. Heinlein mencionó "teoría de juegos" y "teoría de juegos". En la película de 1997 del mismo nombre, el personaje Carl Jenkins se refirió a su misión de inteligencia militar como ser asignado a "juegos y teoría".
- La película de 1964 Dr. Strangelove satiriza ideas teóricas del juego sobre la teoría de la disuasión. Por ejemplo, la disuasión nuclear depende de la amenaza de represalias catastróficamente si se detecta un ataque nuclear. Un teórico del juego podría argumentar que tales amenazas pueden dejar de ser creíble, en el sentido de que pueden conducir a equilibria imperfecta subgame. La película lleva esta idea un paso más allá, con la Unión Soviética comprometiéndose irrevocablemente a una respuesta nuclear catastrófica sin hacer pública la amenaza.
- La banda pop de la década de 1980 Game Theory fue fundada por el cantante / compositor Scott Miller, quien describió el nombre de la banda como alusión a "el estudio de calcular la acción más apropiada dada a un adversario... para darte la cantidad mínima de fracaso".
- Mentiroso juego, un manga japonés de 2005 y la serie de televisión de 2007, presenta los personajes principales en cada episodio con un juego o problema que se dibuja típicamente de la teoría del juego, como lo demuestran las estrategias aplicadas por los personajes.
- La novela de 1974 Spy Story por Len Deighton explora elementos de la teoría del juego en relación con ejercicios del ejército de guerra fría.
- La novela de 2008 El Bosque Oscuro por Liu Cixin explora la relación entre la vida extraterrestre, la humanidad y la teoría del juego.
- El primer antagonista Joker en la película El Caballero Oscuro presenta conceptos teóricos del juego, sobre todo el dilema del prisionero en una escena donde pide a los pasajeros en dos ferries diferentes que bombardee al otro para salvar su propio.
- En la película 2018 asiáticos ricos locos, la líder femenina Rachel Chu es profesora de economía y teoría del juego en la Universidad de Nueva York. Al comienzo de la película ella es vista en su aula de NYU jugando un juego de póquer con su asistente de enseñanza y gana el juego por faroling; luego en el clímax de la película, ella juega un juego de mahjong con la madre desaprobación de su amigo hijo Eleanor, perdiendo el juego a propósito, pero ganando su aprobación como resultado.
Contenido relacionado
Semántica denotacional
Martín Gardner
Aritmética presburger