Teoría de colas

ImprimirCitar

Estudio matemático de líneas de espera, o colas

Las redes de cola son sistemas en los que las colas individuales están conectadas por una red de enrutamiento. En esta imagen, los servidores están representados por círculos, colas por una serie de rectángulos y la red de enrutamiento por flechas. En el estudio de las redes de colas se suele tratar de obtener la distribución del equilibrio de la red, aunque en muchas aplicaciones el estudio del estado transitorio es fundamental.

Teoría de colas es el estudio matemático de las líneas de espera o colas. Se construye un modelo de colas para poder predecir la longitud de las colas y el tiempo de espera. La teoría de colas generalmente se considera una rama de la investigación de operaciones porque los resultados se usan a menudo cuando se toman decisiones comerciales sobre los recursos necesarios para proporcionar un servicio.

La teoría de las colas tiene su origen en la investigación de Agner Krarup Erlang, quien creó modelos para describir el sistema de llamadas entrantes en la empresa de intercambio telefónico de Copenhague. Desde entonces, estas ideas han visto aplicaciones en telecomunicaciones, ingeniería de tráfico, informática, gestión de proyectos y, en particular, ingeniería industrial, donde se aplica en el diseño de fábricas, tiendas, oficinas y hospitales.

Ortografía

La ortografía "en cola" sobre "hacer cola" se encuentra típicamente en el campo de la investigación académica. De hecho, una de las revistas insignia del campo es Queueing Systems.

Nodos de cola únicos

Una cola o nodo de cola se puede considerar casi como una caja negra. Los trabajos (también llamados clientes o solicitudes, según el campo) llegan a la cola, posiblemente esperen algún tiempo, tarden algún tiempo en procesarse, y luego salir de la cola.

Una caja negra. Los trabajos llegan y se alejan de la cola.

Sin embargo, el nodo de cola no es una caja negra pura, ya que se necesita cierta información sobre el interior del nodo de cola. La cola tiene uno o más servidores, cada uno de los cuales puede emparejarse con un trabajo entrante. Cuando el trabajo se complete y se vaya, ese servidor volverá a estar libre para emparejarse con otro trabajo que llegue.

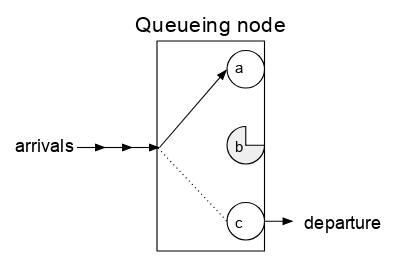
Un nodo de cola con 3 servidores. Servidor a es ocioso, y por lo tanto se le da una llegada al proceso. Servidor b está actualmente ocupado y tomará algún tiempo antes de que pueda completar el servicio de su trabajo. Servidor c acaba de completar el servicio de un trabajo y por lo tanto será el próximo a recibir un trabajo llegado.

Una analogía que se usa a menudo es la del cajero de un supermercado. (Hay otros modelos, pero este se encuentra comúnmente en la literatura). Los clientes llegan, el cajero los procesa y se van. Cada cajero procesa un cliente a la vez y, por lo tanto, este es un nodo de cola con un solo servidor. Una configuración en la que un cliente se irá de inmediato si el cajero está ocupado cuando llegue el cliente se denomina cola sin búfer (o sin área de espera). Una configuración con una zona de espera para hasta n clientes se denomina cola con un búfer de tamaño n.

Proceso nacimiento-muerte

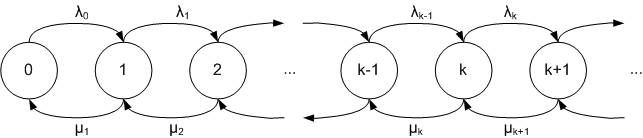
El comportamiento de una sola cola (también llamado nodo de cola) se puede describir mediante un proceso de nacimiento y muerte, que describe las llegadas y salidas de la cola, junto con la cantidad de trabajos actualmente. en el sistema. Si k indica el número de trabajos en el sistema (ya sea en servicio o en espera si la cola tiene un búfer de trabajos en espera), entonces una llegada aumenta k en 1 y un la salida disminuye k en 1.

El sistema pasa entre valores de k por "nacimientos" y "muertos", que ocurren a las tasas de llegada $lambda _{i}$ y las tasas de salida $mu _{i}$ para cada trabajo $i$ . Para una cola, estas tasas se consideran generalmente no variar con el número de puestos de trabajo en la cola, por lo que se asume una tasa media única de llegadas/salidas por unidad de tiempo. En este supuesto, este proceso tiene una tasa de llegada ${displaystyle lambda ={text{avg}}(lambda _{1},lambda _{2},dotslambda _{k})}$ y una tasa de salida ${displaystyle mu ={text{avg}}(mu _{1},mu _{2},dotsmu _{k})}$ .

Un proceso de nacimiento-muerte. Los valores en los círculos representan el estado del sistema, que evoluciona sobre la base de las tasas de llegada λ_i y tasas de salida μ_i.

Una cola con 1 servidor, tasa de llegada λ y tasa de salida μ.

Ecuaciones de equilibrio

Las ecuaciones de estado estables para el proceso de nacimiento y muerte, conocidos como ecuaciones de equilibrio, son las siguientes. Aquí. $P_{n}$ denota la probabilidad constante del estado de estar en estado n.

{displaystyle mu _{1}P_{1}=lambda _{0}P_{0}}

{displaystyle lambda _{0}P_{0}+mu _{2}P_{2}=(lambda _{1}+mu _{1})P_{1}}

{displaystyle lambda _{n-1}P_{n-1}+mu _{n+1}P_{n+1}=(lambda _{n}+mu _{n})P_{n}}

Las dos primeras ecuaciones implican

{displaystyle P_{1}={frac {lambda _{0}}{mu _{1}}}P_{0}}

{displaystyle P_{2}={frac {lambda _{1}}{mu _{2}}}P_{1}+{frac {1}{mu _{2}}}(mu _{1}P_{1}-lambda _{0}P_{0})={frac {lambda _{1}}{mu _{2}}}P_{1}={frac {lambda _{1}lambda _{0}}{mu _{2}mu _{1}}}P_{0}}

Por inducción matemática,

{displaystyle P_{n}={frac {lambda _{n-1}lambda _{n-2}cdots lambda _{0}}{mu _{n}mu _{n-1}cdots mu _{1}}}P_{0}=P_{0}prod _{i=0}^{n-1}{frac {lambda _{i}}{mu _{i+1}}}}

La condición ${displaystyle sum _{n=0}^{infty }P_{n}=P_{0}+P_{0}sum _{n=1}^{infty }prod _{i=0}^{n-1}{frac {lambda _{i}}{mu _{i+1}}}=1}$ conduce a

{displaystyle P_{0}={frac {1}{1+sum _{n=1}^{infty }prod _{i=0}^{n-1}{frac {lambda _{i}}{mu _{i+1}}}}}}

que, junto con la ecuación para $P_{n}$ ${displaystyle (ngeq 1)}$ , describe completamente las probabilidades de estado estable requeridas.

Notación de Kendall

Los nodos de colas individuales generalmente se describen usando la notación de Kendall en la forma A/S/c donde A describe la distribución de duraciones entre cada llegada al cola, S la distribución de tiempos de servicio para trabajos y c la cantidad de servidores en el nodo. Para un ejemplo de la notación, la cola M/M/1 es un modelo simple en el que un solo servidor atiende trabajos que llegan de acuerdo con un proceso de Poisson (donde las duraciones entre llegadas se distribuyen exponencialmente) y tienen tiempos de servicio distribuidos exponencialmente (el M denota un proceso de Markov). En una cola M/G/1, la G significa "general" e indica una distribución de probabilidad arbitraria para los tiempos de servicio.

Ejemplo de análisis de una cola M/M/1

Considere una cola con un servidor y las siguientes características:

$lambda$ : la tasa de llegada (el recíproco del tiempo esperado entre cada cliente que llega, por ejemplo 10 clientes por segundo)
$mu$ : el recíproco del tiempo medio de servicio (el número esperado de finalizaciones de servicio consecutivas por el mismo tiempo unitario, por ejemplo por 30 segundos)
n: el parámetro caracterizando el número de clientes en el sistema
$P_{n}$ : la probabilidad de que haya n clientes en el sistema en estado fijo

Más adelante, $E_{n}$ representa el número de veces que el sistema entra en estado n, y $L_{n}$ representan el número de veces que el sistema deja estado n. Entonces... ${displaystyle leftvert E_{n}-L_{n}rightvert in {0,1}}$ para todos n. Es decir, el número de veces que el sistema deja un estado difiere en la mayoría de 1 del número de veces que entra en ese estado, ya que o bien volverá a ese estado en algún momento en el futuro ( ${displaystyle E_{n}=L_{n}}$ ) o no ( ${displaystyle leftvert E_{n}-L_{n}rightvert =1}$ ).

Cuando el sistema llega a un estado estable, la tasa de llegada debe ser igual a la tasa de salida.

Por lo tanto, las ecuaciones de equilibrio

{displaystyle mu P_{1}=lambda P_{0}}

{displaystyle lambda P_{0}+mu P_{2}=(lambda +mu)P_{1}}

{displaystyle lambda P_{n-1}+mu P_{n+1}=(lambda +mu)P_{n}}

implicar

{displaystyle P_{n}={frac {lambda }{mu }}P_{n-1}, n=1,2,ldots }

El hecho de que ${displaystyle P_{0}+P_{1}+cdots =1}$ conduce a la fórmula de distribución geométrica

{displaystyle P_{n}=(1-rho)rho ^{n}}

Donde $<math alttext="{displaystyle rho ={frac {lambda }{mu }}*** *** =λ λ μ μ .1{displaystyle rho ={frac {fnMicrode - ¿Qué?<img alt="{displaystyle rho ={frac {lambda }{mu }}$ .

Cola simple de dos ecuaciones

Un sistema básico común de colas se atribuye a Erlang y es una modificación de la Ley de Little. Dada una tasa de llegada λ, una tasa de abandono σ y una tasa de salida μ, la longitud de la cola L Se define como:

{displaystyle L={frac {lambda -sigma }{mu }}}

Suponiendo una distribución exponencial de las tarifas, el tiempo de espera W se puede definir como la proporción de llegadas que se atienden. Esto es igual a la tasa de supervivencia exponencial de aquellos que no abandonan durante el período de espera, dando:

{displaystyle {frac {mu }{lambda }}=e^{-W{mu }}}

La segunda ecuación comúnmente se reescribe como:

{displaystyle W={frac {1}{mu }}mathrm {ln} {frac {lambda }{mu }}}

El modelo de caja única de dos etapas es común en epidemiología.

Historia

En 1909, Agner Krarup Erlang, un ingeniero danés que trabajaba para la Central Telefónica de Copenhague, publicó el primer artículo sobre lo que ahora se llamaría teoría de colas. Modeló el número de llamadas telefónicas que llegan a una central mediante un proceso de Poisson y resolvió la cola M/D/1 en 1917 y el modelo de colas M/D/k en 1920. En la notación de Kendall:

M significa "Markov" o "sin memoria", y los medios de llegada se producen según un proceso Poisson
D significa "determinista", y significa que los trabajos que llegan a la cola requieren una cantidad fija de servicio
k describe el número de servidores en el nodo de cola (k = 1, 2, 3,...)

Si el nodo tiene más trabajos que servidores, los trabajos se pondrán en cola y esperarán el servicio.

La cola M/G/1 fue resuelta por Felix Pollaczek en 1930, una solución que más tarde reformuló en términos probabilísticos por Aleksandr Khinchin y que ahora se conoce como la fórmula Pollaczek-Khinchine.

Después de la década de 1940, la teoría de colas se convirtió en un área de interés para la investigación de los matemáticos. En 1953, David George Kendall resolvió la cola GI/M/k e introdujo la notación moderna para colas, ahora conocida como notación de Kendall. En 1957, Pollaczek estudió el GI/G/1 usando una ecuación integral. John Kingman dio una fórmula para el tiempo medio de espera en una cola G/G/1, ahora conocida como fórmula de Kingman.

Leonard Kleinrock trabajó en la aplicación de la teoría de colas a la conmutación de mensajes a principios de la década de 1960 y a la conmutación de paquetes a principios de la década de 1970. Su contribución inicial a este campo fue su tesis doctoral en el Instituto Tecnológico de Massachusetts en 1962, publicada en forma de libro en 1964. Su trabajo teórico publicado a principios de la década de 1970 apoyó el uso de la conmutación de paquetes en ARPANET, un precursor de Internet.

El método geométrico de matriz y los métodos analíticos de matriz han permitido considerar las colas con distribuciones de tiempo de servicio y entre llegadas distribuidas por fase.

Los sistemas con órbitas acopladas son una parte importante de la teoría de colas en la aplicación a redes inalámbricas y procesamiento de señales.

Los problemas como las métricas de rendimiento para la cola M/G/k siguen siendo un problema abierto.

Disciplinas de servicio

Primero en primer lugar (FIFO) cola ejemplo

Se pueden usar varias políticas de programación en los nodos de cola:

Primero en, primero en salir: También se llama primera vez, merecido (FCFS), este principio establece que los clientes se sirven uno a la vez y que el cliente que ha estado esperando el más largo se sirve primero.

La última vez, la primera salida: Este principio también sirve a los clientes una a la vez, pero el cliente con el tiempo de espera más corto será servido primero. También conocido como una pila.

Participación de procesadores: La capacidad de servicio se comparte por igual entre los clientes.

Prioridad: Los clientes con alta prioridad son atendidos primero. Las colas prioritarias pueden ser de dos tipos: no preventiva (donde un trabajo en servicio no puede ser interrumpido) y preventiva (donde un trabajo en servicio puede ser interrumpido por un trabajo de mayor prioridad). No se pierde trabajo en ninguno de los dos modelos.

Trabajo más corto primero: El próximo trabajo a ser servido es el que tiene el tamaño más pequeño.

Trabajo más corto preventivo primero: El próximo trabajo a ser servido es el que tiene el tamaño original más pequeño.

Tiempo de procesamiento más corto: El siguiente trabajo para servir es el que tiene el menor requisito de procesamiento restante.

Servicio de servicios

servidor único: los clientes se alinean y sólo hay un servidor
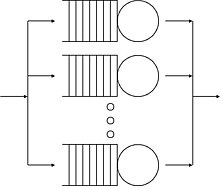
Varios servidores paralelos (single queue): los clientes se alinean y hay varios servidores
Varios servidores paralelos (several colas): hay muchos contadores y los clientes pueden decidir para qué cola

Servidor poco fiable

Las fallas del servidor ocurren según un proceso estocástico (aleatorio) (generalmente Poisson) y son seguidas por períodos de configuración durante los cuales el servidor no está disponible. El cliente interrumpido permanece en el área de servicio hasta que se arregle el servidor.

Comportamiento de espera del cliente

Balking: los clientes deciden no unirse a la cola si es demasiado largo
Jockeying: los clientes cambian entre colas si creen que serán servidos más rápido haciéndolo
Reneging: los clientes dejan la cola si han esperado demasiado tiempo para el servicio

Los clientes que llegan y no se atienden (ya sea porque la cola no tiene búfer o porque el cliente se resiste o se niega) también se conocen como abandonos. La tasa promedio de abandonos es un parámetro importante que describe una cola.

Redes en cola

Las redes de colas son sistemas en los que múltiples colas están conectadas por enrutamiento de clientes. Cuando un cliente recibe servicio en un nodo, puede unirse a otro nodo y hacer cola para el servicio o abandonar la red.

Para redes de m nodos, el estado del sistema se puede describir mediante un vector dimensional m (x₁, x₂,..., x_m) donde x_i representa el número de clientes en cada nodo.

Las redes de colas no triviales más simples se denominan colas en tándem. Los primeros resultados significativos en esta área fueron las redes de Jackson, para las cuales existe una distribución estacionaria en forma de producto eficiente y se puede calcular el análisis del valor medio (que permite métricas promedio como el rendimiento y los tiempos de permanencia). Si el número total de clientes en la red permanece constante, la red se denomina red cerrada y se ha demostrado que también tiene una distribución estacionaria en forma de producto mediante el teorema de Gordon-Newell. Este resultado se extendió a la red BCMP, donde se muestra que una red con tiempos de servicio, regímenes y enrutamiento de clientes muy generales también exhibe una distribución estacionaria en forma de producto. La constante de normalización se puede calcular con el algoritmo de Buzen, propuesto en 1973.

También se han investigado las redes de clientes, como las redes Kelly, donde los clientes de diferentes clases experimentan diferentes niveles de prioridad en diferentes nodos de servicio. Otro tipo de red son las redes G, propuestas por primera vez por Erol Gelenbe en 1993: estas redes no asumen distribuciones temporales exponenciales como la clásica red de Jackson.

Algoritmos de enrutamiento

En redes de tiempo discreto donde existe una restricción sobre qué nodos de servicio pueden estar activos en cualquier momento, el algoritmo de programación de peso máximo elige una política de servicio para brindar un rendimiento óptimo en el caso de que cada trabajo visite solo a una persona. nodo de servicio. En el caso más general en el que los trabajos pueden visitar más de un nodo, el enrutamiento de contrapresión brinda un rendimiento óptimo. Un programador de red debe elegir un algoritmo de cola, que afecta las características de la red más grande.

Límites de campo medio

Los modelos de campo medio consideran el comportamiento limitante de la medida empírica (proporción de colas en diferentes estados) a medida que el número de colas m tiende a infinito. El impacto de otras colas en cualquier cola dada en la red se aproxima mediante una ecuación diferencial. El modelo determinista converge a la misma distribución estacionaria que el modelo original.

Aproximaciones de tráfico pesado/difusión

En un sistema con altas tasas de ocupación (utilización cercana a 1), se puede utilizar una aproximación de tráfico pesado para aproximar el proceso de longitud de la cola mediante un movimiento browniano reflejado, un proceso de Ornstein-Uhlenbeck o un proceso de difusión más general. El número de dimensiones del proceso browniano es igual al número de nodos en cola, con la difusión restringida a la ortante no negativa.

Límites de fluidos

Los modelos fluidos son análogos deterministas continuos de las redes de colas obtenidas al tomar el límite cuando el proceso se escala en el tiempo y el espacio, lo que permite objetos heterogéneos. Esta trayectoria escalada converge a una ecuación determinista que permite probar la estabilidad del sistema. Se sabe que una red de colas puede ser estable pero tener un límite de fluido inestable.

Contenido relacionado

Más resultados...