Teorema fundamental de los homomorfismos

En álgebra abstracta, el teorema fundamental de los homomorfismos, también conocido como teorema fundamental del homomorfismo, o primer teorema del isomorfismo, relaciona la estructura de dos objetos entre los que se da un homomorfismo, y del núcleo e imagen del homomorfismo.

El teorema del homomorfismo se usa para probar los teoremas del isomorfismo.

Versión teórica grupal

Diagrama del teorema fundamental sobre los homomorfismos donde f es un homomorfismo, N es un subgrupo normal de G y e es el elemento de identidad G.

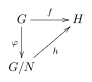
Dados dos grupos G y H y un homomorfismo de grupo f: G → H, sea N un subgrupo normal en G y φ el homomorfismo sobreyectivo natural G → G/N (donde G/N es el grupo cociente de G por N). Si N es un subconjunto de ker(f) entonces existe un homomorfismo único h: G/N → H tal que f = h ∘φ.

En otras palabras, la proyección natural φ es universal entre los homomorfismos en G que asignan N al elemento de identidad.

La situación se describe mediante el siguiente diagrama conmutativo:

h es inyectiva si y solo si N = ker(f). Por lo tanto, al establecer N = ker(f) obtenemos inmediatamente el primer teorema de isomorfismo.

Podemos escribir el enunciado del teorema fundamental sobre homomorfismos de grupos como "toda imagen homomórfica de un grupo es isomorfa a un grupo cociente".

Otras versiones

Teoremas similares son válidos para monoides, espacios vectoriales, módulos y anillos.