Teorema del residuo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Concepto de análisis complejo

En el análisis complejo, el teorema del residuo, a veces llamado teorema del residuo de Cauchy, es una poderosa herramienta para evaluar integrales de línea de funciones analíticas sobre curvas cerradas; a menudo se puede usar para calcular integrales reales y también series infinitas. Generaliza el teorema integral de Cauchy y la fórmula integral de Cauchy. Desde una perspectiva geométrica, se puede ver como un caso especial de Stokes' teorema.

Declaración

La declaración es la siguiente:

Ilustración del escenario.

Sea $U$ un subconjunto abierto simplemente conectado del plano complejo que contiene una lista finita de puntos $a 1,..., a n$ , $U 0 = U {a 1, \dots, a n}$ , y una función $f$ definida y holomorfa en $U 0 . Sea γ una curva cerrada rectificable en U 0, e indica el número de bobinado de γ alrededor de a k por I(γ, a k) . La integral de línea de f alrededor de γ es igual a 2 πi veces la suma de los residuos de f en los puntos, cada uno contado tantas veces como γ se enrolla alrededor del punto:$

{displaystyle oint _{gamma }f(z),dz=2pi isum _{k=1}^{n}operatorname {I} (gammaa_{k})operatorname {Res} (f,a_{k}).}

Si $γ$ es una curva cerrada simple orientada positivamente, $I(γ, a k) = 1$ si $a k$ está en el interior de $γ$ , y 0 si no, por lo tanto

{displaystyle oint _{gamma }f(z),dz=2pi isum operatorname {Res} (f,a_{k})}

a k

γ

La relación del teorema del residuo con el teorema de Stokes' El teorema viene dado por el teorema de la curva de Jordan. La curva plana general $γ$ debe reducirse primero a un conjunto de curvas cerradas simples ${γ i}$ cuyo total es equivalente a $γ$ con fines de integración; esto reduce el problema a encontrar la integral de $f dz$ a lo largo de una curva de Jordan $γ i$ con interior $V. El requisito de que f sea holomorfo en U 0 = U {a k} es equivalente a la afirmación de que el derivada exterior d (f dz) = 0 en <span class="texhtml" U 0$ . Por lo tanto, si dos regiones planas $V$ y $W$ de $U$ encierran el mismo subconjunto ${a j}$ de ${a k}$ , las regiones $V W$ y $W V$ se encuentran completamente en $U 0$ , y por lo tanto

{displaystyle int _{Vsetminus W}d(f,dz)-int _{Wsetminus V}d(f,dz)}

f dz

γ j == V

λ j

a j

f

2 πi

{} a j}

{} γ j}

[I] γ, a k)

Para evaluar integrales reales, se utiliza el teorema de los residuos de la siguiente manera: se extiende el integrando al plano complejo y se calculan sus residuos (que suele ser fácil), y se extiende una parte del eje real a una curva cerrada adjuntando un semicírculo en el semiplano superior o inferior, formando un semicírculo. La integral sobre esta curva se puede calcular usando el teorema del residuo. A menudo, la parte del semicírculo de la integral tenderá hacia cero a medida que crece el radio del semicírculo, dejando solo la parte del eje real de la integral, la que nos interesaba originalmente.

Ejemplos

Una integral a lo largo del eje real

La integral

{displaystyle int _{-infty }^{infty }{frac {e^{itx}}{x^{2}+1}},dx}

El contorno

C

Surge en teoría de probabilidades al calcular la función característica de la distribución de Cauchy. Resiste las técnicas del cálculo elemental pero puede evaluarse expresándolo como un límite de integrales de contorno.

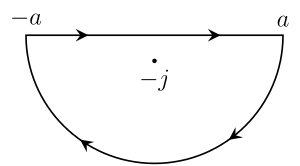
Suponga que $t > 0$ y define el contorno $C$ que va a lo largo de la línea real desde $- a$ a $a$ y luego en sentido antihorario a lo largo de un semicírculo centrado en 0 desde $a$ a $- a$ . Tome $a$ como mayor que 1, de modo que la unidad imaginaria $i$ está dentro de la curva. Ahora considere la integral de contorno

{displaystyle int _{C}{f(z)},dz=int _{C}{frac {e^{itz}}{z^{2}+1}},dz.}

Dado que $e itz$ es una función completa (sin singularidades en ningún punto en el plano complejo), esta función tiene singularidades solo donde el denominador $z 2 + 1$ es cero. Dado que $z 2 + 1 = (z + i)(z - i)$ , eso sucede solo donde $z = i$ o $z = - i$ . Solo uno de esos puntos está en la región delimitada por este contorno. Porque $f (z)$ es

{displaystyle {begin{aligned}{frac {e^{itz}}{z^{2}+1}}&={frac {e^{itz}}{2i}}left({frac {1}{z-i}}-{frac {1}{z+i}}right)\&={frac {e^{itz}}{2i(z-i)}}-{frac {e^{itz}}{2i(z+i)}},end{aligned}}}

f () z)

z = i

{displaystyle operatorname {Res} _{z=i}f(z)={frac {e^{-t}}{2i}}.}

Según el teorema del residuo, entonces, tenemos

{displaystyle int _{C}f(z),dz=2pi icdot operatorname {Res} limits _{z=i}f(z)=2pi i{frac {e^{-t}}{2i}}=pi e^{-t}.}

El contorno $C$ se puede dividir en una parte recta y un arco curvo, de modo que

{displaystyle int _{mathrm {straight} }f(z),dz+int _{mathrm {arc} }f(z),dz=pi e^{-t}}

{displaystyle int _{-a}^{a}f(z),dz=pi e^{-t}-int _{mathrm {arc} }f(z),dz.}

Usando algunas estimaciones, tenemos

{displaystyle left|int _{mathrm {arc} }{frac {e^{itz}}{z^{2}+1}},dzright|leq pi acdot sup _{text{arc}}left|{frac {e^{itz}}{z^{2}+1}}right|leq pi acdot sup _{text{arc}}{frac {1}{|z^{2}+1|}}leq {frac {pi a}{a^{2}-1}},}

{displaystyle lim _{ato infty }{frac {pi a}{a^{2}-1}}=0.}

La estimación en el numerador sigue desde $t > 0$ , y para números complejos $z$ a lo largo del arco (que se encuentra en el semiplano superior), el argumento $φ$ de $z$ mentiras entre 0 y $π$ . Entonces,

{displaystyle left|e^{itz}right|=left|e^{it|z|(cos varphi +isin varphi)}right|=left|e^{-t|z|sin varphi +it|z|cos varphi }right|=e^{-t|z|sin varphi }leq 1.}

Por lo tanto,

{displaystyle int _{-infty }^{infty }{frac {e^{itz}}{z^{2}+1}},dz=pi e^{-t}.}

Si $t < 0$ luego un argumento similar con un arco $C'$ que gira alrededor de $- i$ en lugar de $i$ muestra que

El contorno

C .

{displaystyle int _{-infty }^{infty }{frac {e^{itz}}{z^{2}+1}},dz=pi e^{t},}

y finalmente tenemos

{displaystyle int _{-infty }^{infty }{frac {e^{itz}}{z^{2}+1}},dz=pi e^{-left|tright|}.}

(Si $t = 0$ entonces la integral cede inmediatamente a los métodos de cálculo elemental y su valor es $π$ .)

Una suma infinita

El hecho de que $π cot(πz)$ tenga polos simples con residuo 1 en cada entero se puede usar para calcular la suma

{displaystyle sum _{n=-infty }^{infty }f(n).}

Considere, por ejemplo, $f (z) = z -2$ . Sea $Γ N$ el rectángulo que es el límite de $[- N - 1 / 2, N + 1 / 2] 2$ con orientación positiva, con un número entero $N$ . Por la fórmula del residuo,

{displaystyle {frac {1}{2pi i}}int _{Gamma _{N}}f(z)pi cot(pi z),dz=operatorname {Res} limits _{z=0}+sum _{n=-N atop nneq 0}^{N}n^{-2}.}

El lado izquierdo va a cero como $N \to$ desde que el integrante tiene orden ${displaystyle O(n^{-2})}$ . Por otro lado,

{displaystyle {frac {z}{2}}cot left({frac {z}{2}}right)=1-B_{2}{frac {z^{2}}{2!}}+cdots }

{displaystyle B_{2}={frac {1}{6}}.}

(De hecho, $z / 2 cot(z / 2) = iz / 1 - e - iz - iz / 2$ .) Por lo tanto, el residuo $Res z =0$ es $- π 2 / 3$ . Concluimos:

{displaystyle sum _{n=1}^{infty }{frac {1}{n^{2}}}={frac {pi ^{2}}{6}}}

El mismo truco se puede utilizar para establecer la suma de la serie de Eisenstein:

{displaystyle pi cot(pi z)=lim _{Nto infty }sum _{n=-N}^{N}(z-n)^{-1}.}

Tomamos $f (z) = (w - z) -1$ con $w$ un número no entero y mostraremos lo anterior para $w$ . La dificultad en este caso es mostrar la desaparición de la integral de contorno en el infinito. Tenemos:

{displaystyle int _{Gamma _{N}}{frac {pi cot(pi z)}{z}},dz=0}

{displaystyle int _{Gamma _{N}}f(z)pi cot(pi z),dz=int _{Gamma _{N}}left({frac {1}{w-z}}+{frac {1}{z}}right)pi cot(pi z),dz}

N \to

Contenido relacionado

Más resultados...