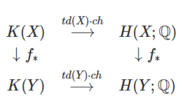Teorema del índice de Atiyah-Singer

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Resultado matemático en geometría diferencial

En geometría diferencial, el teorema del índice de Atiyah–Singer, demostrado por Michael Atiyah e Isadore Singer (1963), establece que para un operador diferencial elíptico en una variedad compacta, el índice analítico (relacionado con la dimensión del espacio de soluciones) es igual al índice topológico (definido en términos de algunos datos topológicos). Incluye muchos otros teoremas, como el teorema de Chern-Gauss-Bonnet y el teorema de Riemann-Roch, como casos especiales, y tiene aplicaciones a la física teórica.

Historia

El problema de índice para operadores diferenciales elípticos fue planteado por Israel Gel'fand. Se dio cuenta de la invariancia homotópica del índice y pidió una fórmula por medio de invariantes topológicos. Algunos de los ejemplos motivadores incluyeron el teorema de Riemann-Roch y su generalización, el teorema de Hirzebruch-Riemann-Roch, y el teorema de la firma de Hirzebruch. Friedrich Hirzebruch y Armand Borel habían demostrado la integralidad del género Â de una variedad de espín, y Atiyah sugirió que esta integralidad podría explicarse si fuera el índice del operador de Dirac (que fue redescubierto por Atiyah y Singer en 1961).

El teorema de Atiyah-Singer se anunció en 1963. La prueba esbozada en este anuncio nunca fue publicada por ellos, aunque aparece en el libro de Palais. Aparece también en el "Séminaire Cartan-Schwartz 1963/64" que se llevó a cabo en París simultáneamente con el seminario dirigido por Richard Palais en la Universidad de Princeton. La última charla en París fue de Atiyah sobre variedades con límite. Su primera prueba publicada reemplazó la teoría del cobordismo de la primera prueba con la teoría K, y usaron esto para dar pruebas de varias generalizaciones en otra secuencia de artículos.

1965: Sergey P. Novikov publicó sus resultados sobre la invariancia topológica de las clases de Pontryagin racionales sobre los manifolds suaves.
Los resultados de Robion Kirby y Laurent C. Siebenmann, combinados con el periódico de René Thom, demostraron la existencia de clases de Pontryagin racionales en múltiples ejes topológicos. Las clases de Pontryagin racionales son ingredientes esenciales del teorema de índice en los múltiples suaves y topológicos.
1969: Michael Atiyah define operadores elípticos abstractos en espacios métricos arbitrarios. Los operadores elípticos abstractos se convirtieron en protagonistas de la teoría de Kasparov y la geometría diferencial no transmutante de Connes.
1971: Isadore Singer propone un programa integral para futuras extensiones de la teoría del índice.
1972: Gennadi G. Kasparov publica su trabajo sobre la realización de la K-homología por operadores elípticos abstractos.
1973: Atiyah, Raoul Bott, y Vijay Patodi dieron una nueva prueba del teorema del índice utilizando la ecuación de calor, descrita en un papel de Melrose.
1977: Dennis Sullivan establece su teorema sobre la existencia y singularidad de Lipschitz y estructuras cuasiconformales en múltiples ejes topológicos de dimensión diferentes de 4.
1983: Ezra Getzler motivado por ideas de Edward Witten y Luis Alvarez-Gaume, dio una prueba corta del teorema de índice local para operadores que son locales operadores de Dirac; esto cubre muchos de los casos útiles.
1983: Nicolae Teleman demuestra que los índices analíticos de los operadores de firmas con valores en paquetes vectoriales son invariantes topológicos.
1984: Teleman establece el teorema de índice en los múltiples topológicos.
1986: Alain Connes publica su papel fundamental sobre geometría no transmutante.
1989: Simon K. Donaldson y Sullivan estudian la teoría Yang-Mills sobre los múltiples cuasiconformes de la dimensión 4. Presentan al operador de firmas S definido en formas diferenciales del grado dos.
1990: Connes y Henri Moscovici demuestran la fórmula del índice local en el contexto de la geometría no transmutante.
1994: Connes, Sullivan y Teleman prueban el teorema de índice para los operadores de firmas en los múltiples cuasiconformes.

Notación

X es un manifold compacto suave (sin límite).
E y F son los paquetes vectoriales lisos sobre X.
D es un operador diferencial elíptico de E a F. Así que en las coordenadas locales actúa como un operador diferencial, tomando secciones lisas E a secciones lisas F.

Símbolo de un operador diferencial

Si D es un operador diferencial en un espacio de orden Euclideano n dentro k variables ${displaystyle x_{1},dotsx_{k}}$ , entonces su símbolo es la función de 2k variables ${displaystyle x_{1},dotsx_{k},y_{1},dotsy_{k}}$ , dado por la caída de todos los términos de orden menos que n y sustitución ${displaystyle partial /partial x_{i}}$ por $y_{i}$ . Así que el símbolo es homogéneo en las variables Sí., de grado n. El símbolo está bien definido, aunque ${displaystyle partial /partial x_{i}}$ no se comunica con $x_{i}$ porque guardamos sólo los términos de orden más altos y operadores diferenciales conmutan "hasta términos de orden inferior". El operador se llama elíptico si el símbolo no es cero cuando al menos uno Sí. No es cero.

Ejemplo: El operador de Laplace en k variables tiene símbolo ${displaystyle y_{1}^{2}+cdots +y_{k}^{2}}$ , y así es elíptico ya que esto no es cero cuando cualquiera de los $y_{i}$ No es cero. El operador de onda tiene símbolo ${displaystyle -y_{1}^{2}+cdots +y_{k}^{2}}$ , que no es elíptico si $kgeq 2$ , como el símbolo desaparece para algunos valores no cero de los Sí.s.

El símbolo de un operador diferencial de orden n en una variedad suave X se define de la misma manera utilizando gráficos de coordenadas locales y es una función en la cotangente haz de X, homogéneo de grado n en cada espacio cotangente. (En general, los operadores diferenciales se transforman de una manera bastante complicada bajo transformaciones de coordenadas (ver jet bundle); sin embargo, los términos de mayor orden se transforman como tensores, por lo que obtenemos funciones homogéneas bien definidas en los espacios cotangentes que son independientes de la elección de gráficos locales.) De forma más general, el símbolo de un operador diferencial entre dos paquetes vectoriales E y F es una sección del pullback del paquete Hom(E, F) al espacio cotangente de X. El operador diferencial se llama elíptico si el elemento de Hom(E_x, F_x) es invertible para todos los vectores cotangentes distintos de cero en cualquier punto x de X.

Una propiedad clave de los operadores elípticos es que son casi invertibles; esto está estrechamente relacionado con el hecho de que sus símbolos son casi invertibles. Más precisamente, un operador elíptico D en una variedad compacta tiene una paramétrica (no única) (o pseudoinversa) D′ tal que DD′ -1 y D′D -1 son ambos operadores compactos. Una consecuencia importante es que el kernel de D es de dimensión finita, porque todos los espacios propios de los operadores compactos, excepto el kernel, son de dimensión finita. (El pseudoinverso de un operador diferencial elíptico casi nunca es un operador diferencial. Sin embargo, es un operador pseudodiferencial elíptico).

Índice analítico

Como el operador diferencial elíptico D tiene un pseudoinverso, es un operador de Fredholm. Cualquier operador de Fredholm tiene un índice, definido como la diferencia entre la dimensión (finita) del núcleo de D (soluciones de Df = 0), y la dimensión (finita) del cokernel de D (las restricciones en el lado derecho de una ecuación no homogénea como Df = g, o de manera equivalente el núcleo del operador adjunto). En otras palabras,

ÍndiceD) = dim Ker(D) − dim Coker(D) = dim Ker(D) − dim Ker(D*).

Esto a veces se llama el índice analítico de D.

Ejemplo: Suponga que la variedad es el círculo (considerado como R/Z) y D es el operador d/dx − λ para alguna constante compleja λ. (Este es el ejemplo más simple de un operador elíptico). Entonces el núcleo es el espacio de múltiplos de exp(λx) si λ es un múltiplo entero de 2πi y es 0 de lo contrario, y el núcleo del adjunto es un espacio similar con λ reemplazado por su complejo conjugado. Así que D tiene índice 0. Este ejemplo muestra que el kernel y el cokernel de los operadores elípticos pueden saltar discontinuamente a medida que varía el operador elíptico, por lo que no existe una buena fórmula para sus dimensiones en términos de datos topológicos continuos. Sin embargo, los saltos en las dimensiones del núcleo y el conúcleo son los mismos, por lo que el índice, dado por la diferencia de sus dimensiones, varía de hecho de forma continua y se puede dar en términos de datos topológicos mediante el teorema del índice.

Índice topológico

El índice topológico de un operador diferencial elíptico $D$ entre los paquetes vectoriales lisos $E$ y $F$ on an $n$ - colector compacto de dimensiones $X$ es dado por

{displaystyle (-1)^{n}operatorname {ch} (D)operatorname {Td} (X)[X]=(-1)^{n}int _{X}operatorname {ch} (D)operatorname {Td} (X)}

en otras palabras el valor del componente dimensional superior de la clase mixta de cohomología ${displaystyle operatorname {ch} (D)operatorname {Td} (X)}$ en la clase de homología fundamental del múltiple $X$ hasta una diferencia de señal. Aquí,

${displaystyle operatorname {Td} (X)}$ es la clase Todd del paquete tangente complejo $X$ .
ch⁡ ⁡ ()D){displaystyle operatorname {ch} (D)} ${displaystyle operatorname {ch} (D)}$ es igual a φ φ − − 1()ch⁡ ⁡ ()d()pAlternativa Alternativa E,pAlternativa Alternativa F,σ σ ()D)))){displaystyle varphi ^{-1}(operatorname {ch} (d(p^{*}E,p^{*}F,sigma (D))})} ${displaystyle varphi ^{-1}(operatorname {ch} (d(p^{*}E,p^{*}F,sigma (D))))}$ , donde
- ${displaystyle varphi:H^{k}(X;mathbb {Q})to H^{n+k}(B(X)/S(X);mathbb {Q})}$ es el isomorfismo de Thom para el paquete de la esfera ${displaystyle p:B(X)/S(X)to X}$
- ${displaystyle operatorname {ch}:K(X)otimes mathbb {Q} to H^{*}(X;mathbb {Q})}$ es el personaje de Chern
- ${displaystyle d(p^{*}E,p^{*}F,sigma (D))}$ es el "elemento de diferencia" en ${displaystyle K(B(X)/S(X))}$ asociado a dos paquetes vectoriales ${displaystyle p^{*}E}$ y ${displaystyle p^{*}F}$ on ${displaystyle B(X)}$ y un isomorfismo ${displaystyle sigma (D)}$ entre ellos en el subespacio $S(X)$ .
- ${displaystyle sigma (D)}$ es el símbolo de $D$

En algunas situaciones, es posible simplificar la fórmula anterior con fines computacionales. En particular, si $X$ es un $2m$ - dimensionalmente orientable (compacto) manifold con no-cero Clase Euler ${displaystyle e(TX)}$ , luego aplicar el isomorfismo de Thom y dividir por la clase Euler, el índice topológico puede ser expresado como

{displaystyle (-1)^{m}int _{X}{frac {operatorname {ch} (E)-operatorname {ch} (F)}{e(TX)}}operatorname {Td} (X)}

donde la división tiene sentido tirando ${displaystyle e(TX)^{-1}}$ del anillo de cohomología del espacio de clasificación ${displaystyle BSO}$ .

También se puede definir el índice topológico usando solo la teoría K (y esta definición alternativa es compatible en cierto sentido con la construcción de caracteres de Chern anterior). Si X es una subvariedad compacta de una variedad Y entonces hay un mapa pushforward (o "chillido") de K(TX) a K(TY). El índice topológico de un elemento de K(TX) se define como la imagen de esta operación con Y algún espacio euclidiano, para el cual K(TY) se puede identificar naturalmente con los enteros Z (como consecuencia de la periodicidad de Bott). Este mapa es independiente de la incrustación de X en el espacio euclidiano. Ahora, un operador diferencial como el anterior define naturalmente un elemento de K(TX), y la imagen en Z debajo de este mapa "es" el índice topológico.

Como de costumbre, D es un operador diferencial elíptico entre paquetes vectoriales E y F sobre una variedad compacta X.

El problema del índice es el siguiente: calcular el índice (analítico) de D usando solo el símbolo s y topológico datos derivados de la variedad y el paquete vectorial. El teorema del índice de Atiyah-Singer resuelve este problema y establece:

El índice analítico D es igual a su índice topológico.

A pesar de su formidable definición, el índice topológico suele ser fácil de evaluar de forma explícita. Entonces esto hace posible evaluar el índice analítico. (El conúcleo y el núcleo de un operador elíptico son, en general, extremadamente difíciles de evaluar individualmente; el teorema del índice muestra que, por lo general, al menos podemos evaluar su diferencia). Muchos invariantes importantes de una variedad (como el firma) se puede dar como el índice de operadores diferenciales adecuados, por lo que el teorema del índice nos permite evaluar estos invariantes en términos de datos topológicos.

Aunque el índice analítico suele ser difícil de evaluar directamente, al menos obviamente es un número entero. El índice topológico es, por definición, un número racional, pero por lo general no es del todo obvio a partir de la definición que también es integral. Entonces, el teorema del índice de Atiyah-Singer implica algunas propiedades de integralidad profundas, ya que implica que el índice topológico es integral.

El índice de un operador diferencial elíptico obviamente desaparece si el operador es autoadjunto. También se anula si la variedad X tiene una dimensión impar, aunque hay operadores elípticos pseudodiferenciales cuyo índice no se anula en dimensiones impares.

Relación con Grothendieck-Riemann-Roch

El teorema de Grothendieck–Riemann–Roch fue una de las principales motivaciones detrás del teorema de índice porque el teorema de índice es la contraparte de este teorema en el entorno de los verdaderos múltiples. Ahora, si hay un mapa $f:Xto Y$ de estilizadas compactas casi complejas, entonces hay un diagrama conmutativo

si ${displaystyle Y=*}$ es un punto, entonces recuperamos la declaración anterior. Aquí. $K(X)$ es el grupo Grothendieck de complejos paquetes vectoriales. Este diagrama comunicativo es formalmente muy similar al teorema GRR porque los grupos de cohomología a la derecha son reemplazados por el anillo Chow de una variedad suave, y el grupo Grothendieck a la izquierda es dado por el grupo Grothendieck de paquetes vectoriales algebraicos.

Extensiones del teorema del índice de Atiyah-Singer

Teorema del índice de Teleman

Did you mean:

Due to (Telemann 1983), (Telemann 1984):

Para cualquier operador elíptico abstracto (Atiyah 1970) en un conjunto cerrado, orientado, topológico, el índice analítico equivale al índice topológico.

La prueba de este resultado pasa por consideraciones específicas, incluida la extensión de la teoría de Hodge sobre variedades combinatorias y de Lipschitz (Teleman 1980), (Teleman 1983), la extensión del operador característico de Atiyah–Singer a las variedades de Lipschitz (Teleman 1983), la homología K de Kasparov (Kasparov 1972) y el cobordismo topológico (Kirby & Siebenmann 1977).

Este resultado muestra que el teorema del índice no es simplemente un enunciado de diferenciabilidad, sino un enunciado topológico.

Teorema del índice de Connes-Donaldson-Sullivan-Teleman

Debido a (Donaldson & Sullivan 1989), (Connes, Sullivan & Teleman 1994):

Para cualquier doble cuasiconformal existe una construcción local de las clases características de Hirzebruch-Thom.

Esta teoría se basa en un operador de firma S, definido en formas diferenciales de grado medio en variedades cuasiconformes de dimensión uniforme (compárese con (Donaldson & Sullivan 1989)).

Usando el cobordismo topológico y la homología K, se puede proporcionar una declaración completa de un teorema de índice sobre variedades cuasiconformes (consulte la página 678 de (Connes, Sullivan & Teleman 1994)). El trabajo (Connes, Sullivan & Teleman 1994) "proporciona construcciones locales para clases de características basadas en parientes dimensionales superiores del mapeo medible de Riemann en la dimensión dos y la teoría de Yang-Mills en la dimensión cuatro."

Estos resultados constituyen avances significativos en la línea del programa Perspectivas en Matemáticas de Singer (Singer 1971). Al mismo tiempo, proporcionan, también, una construcción eficaz de las clases racionales de Pontrjagin sobre variedades topológicas. El artículo (Teleman 1985) proporciona un vínculo entre la construcción original de Thom de las clases racionales de Pontrjagin (Thom 1956) y la teoría de índices.

Es importante mencionar que la fórmula del índice es una declaración topológica. Las teorías de obstrucción de Milnor, Kervaire, Kirby, Siebenmann, Sullivan, Donaldson muestran que solo una minoría de las variedades topológicas poseen estructuras diferenciables y estas no son necesariamente únicas. El resultado de Sullivan sobre Lipschitz y estructuras cuasiconformales (Sullivan 1979) muestra que cualquier variedad topológica en dimensión diferente de 4 posee una estructura que es única (hasta la isotopía cercana a la identidad).

Las estructuras cuasiconformales (Connes, Sullivan & Teleman 1994) y más generalmente las estructuras L^p, p > n(n+1)/2, presentado por M. Hilsum (Hilsum 1999), son las estructuras analíticas más débiles en variedades topológicas de dimensión n para los que se sabe que se cumple el teorema del índice.

Otras extensiones

El teorema de Atiyah-Singer se aplica a los operadores pseudodiferenciales elípticos de la misma manera que a los operadores diferenciales elípticos. De hecho, por razones técnicas la mayoría de las pruebas tempranas trabajaron con operadores pseudodiferenciales en lugar de operadores diferenciales: su flexibilidad extra hizo algunos pasos de las pruebas más fáciles.
En lugar de trabajar con un operador elíptico entre dos paquetes vectoriales, a veces es más conveniente trabajar con un complejo elíptico ${displaystyle 0rightarrow E_{0}rightarrow E_{1}rightarrow E_{2}rightarrow dotsm rightarrow E_{m}rightarrow 0}$ de vectores. La diferencia es que los símbolos ahora forman una secuencia exacta (de la sección cero). En el caso de que haya sólo dos paquetes no cero en el complejo esto implica que el símbolo es un isomorfismo fuera de la sección cero, por lo que un complejo elíptico con 2 términos es esencialmente el mismo que un operador elíptico entre dos paquetes vectoriales. Por el contrario, el teorema de índice para un complejo elíptico puede reducirse fácilmente al caso de un operador elíptico: los dos paquetes vectoriales son dados por las sumas de los términos uniformes o impares del complejo, y el operador elíptico es la suma de los operadores del complejo elíptico y sus conjuntos, restringidos a la suma de los incluso paquetes.
Si se permite que el múltiple tenga límites, hay que poner algunas restricciones en el dominio del operador elíptico para asegurar un índice finito. Estas condiciones pueden ser locales (como exigir que las secciones del dominio se desvanezcan en el límite) o condiciones globales más complicadas (como exigir que las secciones del dominio solucionen alguna ecuación diferencial). The local case was worked out by Atiyah and Bott, but they showed that many interesting operators (e.g., the signature operator) do not admit local boundary conditions. Para manejar estos operadores, Atiyah, Patodi y Singer introdujeron condiciones de límites globales equivalentes a adjuntar un cilindro al doble a lo largo del límite y luego restringir el dominio a aquellas secciones que son cuadradas integrado a lo largo del cilindro. Este punto de vista se adopta en la prueba de Melrose (1993) del teorema de índice Atiyah-Patodi-Singer.
En lugar de un solo operador elíptico, se puede considerar una familia de operadores elípticos parametizada por algún espacio Y. En este caso el índice es un elemento de la teoría K de YEn lugar de un entero. Si los operadores de la familia son reales, entonces el índice se encuentra en la verdadera teoría K de Y. Esto da un poco más de información, como el mapa de la verdadera teoría K Y a la teoría K compleja no siempre es inyectable.
Si hay una acción de grupo de un grupo G en el manifold compacto X, comportándose con el operador elíptico, entonces uno reemplaza la teoría K común con la teoría K equivariante. Además, se obtienen generalizaciones del teorema de punto fijo Lefschetz, con términos procedentes de submanifolds de punto fijo del grupo G. Vea también: teorema de índice equivariante.
Atiyah (1976) mostró cómo extender el teorema de índice a algunos manifolds no-compactos, actuados por un grupo discreto con cociente compacto. El núcleo del operador elíptico es en general infinita dimensional en este caso, pero es posible obtener un índice finito utilizando la dimensión de un módulo sobre un álgebra von Neumann; este índice es en general real en lugar de valor entero. Esta versión se llama L² index theorem, y fue utilizado por Atiyah & Schmid (1977) para redireccionar propiedades de la serie discreta representaciones de grupos semisimple Lie.
El teorema de índice de Callias es un teorema de índice para un operador de Dirac en un espacio extradimensional no completo. El índice Atiyah-Singer sólo se define en espacios compactos y desaparece cuando su dimensión es extraña. En 1978 Constantine Callias, por sugerencia de su consejero de doctorado Roman Jackiw, utilizó la anomalía axial para derivar este teorema de índice en los espacios equipados con una matriz hermitiana llamada campo Higgs. El índice del operador Dirac es un invariante topológico que mide el bobinado del campo Higgs en una esfera en el infinito. Si U es la matriz de la unidad en la dirección del campo Higgs, entonces el índice es proporcional a la integral de U()dU)ⁿ⁻¹ sobre eln1) - esfera en el infinito. Si n es incluso, siempre es cero.
- La interpretación topológica de este invariante y su relación con el índice Hörmander propuesto por Boris Fedosov, generalizada por Lars Hörmander, fue publicada por Raoul Bott y Robert Thomas Seeley.

Ejemplos

Teorema de Chern-Gauss-Bonnet

Supongamos que $M$ es un conjunto compacto orientado de la dimensión ${displaystyle n=2r}$ . Si tomamos ${displaystyle Lambda ^{text{even}}}$ para ser la suma de las potencias incluso exteriores del paquete cotangente, y ${displaystyle Lambda ^{text{odd}}}$ ser la suma de los poderes extraños, definir ${displaystyle D=d+d^{*}}$ , considerado como un mapa de ${displaystyle Lambda ^{text{even}}}$ a ${displaystyle Lambda ^{text{odd}}}$ . Luego el índice analítico $D$ es la característica de Euler ${displaystyle chi (M)}$ de la cohomología Hodge $M$ , y el índice topológico es la parte integral de la clase Euler sobre el múltiple. La fórmula índice para este operador produce el teorema Chern–Gauss–Bonnet.

El cálculo concreto es el siguiente: según una variación del principio de división, si $E$ es un verdadero vector de paquete de dimensión ${displaystyle n=2r}$ , para probar afirmaciones que implican clases características, podemos suponer que hay paquetes de líneas complejas ${displaystyle l_{1},,ldots,l_{r}}$ tales que ${displaystyle Eotimes mathbb {C} =l_{1}oplus {overline {l_{1}}}oplus dotsm l_{r}oplus {overline {l_{r}}}}$ . Por lo tanto, podemos considerar las raíces de Chern ${displaystyle x_{i}(Eotimes mathbb {C})=c_{1}(l_{i})}$ , ${displaystyle x_{r+i}(Eotimes mathbb {C})=c_{1}{mathord {left({overline {l_{i}}}right)}}=-x_{i}(Eotimes mathbb {C})}$ , ${displaystyle i=1,,ldots,r}$ .

Usando las raíces de Chern como arriba y las propiedades estándar de la clase Euler, tenemos que ${textstyle e(TM)=prod _{i}^{r}x_{i}(TMotimes mathbb {C})}$ . En cuanto al personaje de Chern y la clase Todd,

<math alttext="{displaystyle {begin{aligned}operatorname {ch} {mathord {left(Lambda ^{text{even}}-Lambda ^{text{odd}}right)}}&=1-operatorname {ch} (T^{*}Motimes mathbb {C})+operatorname {ch} {mathord {left(Lambda ^{2}T^{*}Motimes mathbb {C} right)}}-ldots +(-1)^{n}operatorname {ch} {mathord {left(Lambda ^{n}T^{*}Motimes mathbb {C} right)}}\&=1-sum _{i}^{n}e^{-x_{i}}(TMotimes mathbb {C})+sum _{ich⁡ ⁡ ()▪ ▪ incluso− − ▪ ▪ extraño)=1− − ch⁡ ⁡ ()TAlternativa Alternativa M⊗ ⊗ C)+ch⁡ ⁡ ()▪ ▪ 2TAlternativa Alternativa M⊗ ⊗ C)− − ...... +()− − 1)nch⁡ ⁡ ()▪ ▪ nTAlternativa Alternativa M⊗ ⊗ C)=1− − .. ine− − xi()TM⊗ ⊗ C)+.. i.je− − xie− − xj()TM⊗ ⊗ C)+...... +()− − 1)ne− − x1⋯ ⋯ e− − xn()TM⊗ ⊗ C)=∏ ∏ in()1− − e− − xi)()TM⊗ ⊗ C)Td⁡ ⁡ ()TM⊗ ⊗ C)=∏ ∏ inxi1− − e− − xi()TM⊗ ⊗ C){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} ¿Por qué? TMotimes mathbb {C}+ldots +(-1)^{n}e^{-x_{1}dotsm e^{-x_{n}(TMotimes mathbb {C})\\\cH00=prod ¿Por qué? {Td} (TMotimes mathbb {C}) sensible=prod _{i}{n}{frac {cHFF} {cHFF} {cHFF}} {cHFF}} {cHFF} {cHFF}}} {cHFF}}} {cH}}}} {cH}}}} {cH}}} {cH}}}} {cH}}}}}}} {cH}}}}}}}}}}}}}}} {cH}}}}}}}}}}}}} {c}}}}} {c}}}}}}}} {ccccH}}}}}}}}}}}}}}}}}}}}}} {cH}}} {cH}}}} {c}}}}}}}}} {cH}}}}}}}} {cH}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { TMotimes mathbb {C}end{aligned}<img alt="{displaystyle {begin{aligned}operatorname {ch} {mathord {left(Lambda ^{text{even}}-Lambda ^{text{odd}}right)}}&=1-operatorname {ch} (T^{*}Motimes mathbb {C})+operatorname {ch} {mathord {left(Lambda ^{2}T^{*}Motimes mathbb {C} right)}}-ldots +(-1)^{n}operatorname {ch} {mathord {left(Lambda ^{n}T^{*}Motimes mathbb {C} right)}}\&=1-sum _{i}^{n}e^{-x_{i}}(TMotimes mathbb {C})+sum _{i

Aplicando el teorema del índice,

{displaystyle chi (M)=(-1)^{r}int _{M}{frac {prod _{i}^{n}left(1-e^{-x_{i}}right)}{prod _{i}^{r}x_{i}}}prod _{i}^{n}{frac {x_{i}}{1-e^{-x_{i}}}}(TMotimes mathbb {C})=(-1)^{r}int _{M}(-1)^{r}prod _{i}^{r}x_{i}(TMotimes mathbb {C})=int _{M}e(TM)}

Did you mean:

which is the "topological#34; version of the Chern-Gauss-Bonnet theorem (the geometric one being obtained by applying the Chern-Weil homomorphism).

Teorema de Hirzebruch-Riemann-Roch

Tomemos X como una variedad compleja de dimensión (compleja) n con un haz vectorial holomorfo V. Sean las cestas vectoriales E y F las sumas de las cestas de formas diferenciales con coeficientes en V de tipo (0, i) con i par o impar, y dejamos que el operador diferencial D sea la suma

overline partial +overline partial ^{*}

restringido a E.

Esta derivación del teorema de Hirzebruch-Riemann-Roch es más natural si usamos el teorema del índice para complejos elípticos en lugar de operadores elípticos. Podemos tomar el complejo como

{displaystyle 0rightarrow Vrightarrow Votimes Lambda ^{0,1}T^{*}(X)rightarrow Votimes Lambda ^{0,2}T^{*}(X)rightarrow dotsm }

con la diferencia dada por $overlinepartial$ . Entonces el i 'grupo de cohomología es sólo el grupo coherente de cohomología Hⁱ()X, V), por lo que el índice analítico de este complejo es la característica del Euler holomorfo V:

{displaystyle operatorname {index} (D)=sum _{p}(-1)^{p}dim H^{p}(X,V)=chi (X,V)}

Dado que estamos tratando con paquetes complejos, la computación del índice topológico es más simple. Usando las raíces de Chern y haciendo computaciones similares como en el ejemplo anterior, la clase Euler es dada por ${textstyle e(TX)=prod _{i}^{n}x_{i}(TX)}$ y

{displaystyle {begin{aligned}operatorname {ch} left(sum _{j}^{n}(-1)^{j}Votimes Lambda ^{j}{overline {T^{*}X}}right)&=operatorname {ch} (V)prod _{j}^{n}left(1-e^{x_{j}}right)(TX)\operatorname {Td} (TXotimes mathbb {C})=operatorname {Td} (TX)operatorname {Td} left({overline {TX}}right)&=prod _{i}^{n}{frac {x_{i}}{1-e^{-x_{i}}}}prod _{j}^{n}{frac {-x_{j}}{1-e^{x_{j}}}}(TX)end{aligned}}}

Aplicando el teorema del índice, obtenemos el teorema de Hirzebruch-Riemann-Roch:

{displaystyle chi (X,V)=int _{X}operatorname {ch} (V)operatorname {Td} (TX)}

Did you mean:

In fact we get a generalization of it to all complex manifolds: Hirzebruch 's proof only worked for projective complex manifolds X.

Teorema de la firma de Hirzebruch

El teorema de la firma de Hirzebruch establece que la firma de una variedad compacta orientada X de dimensión 4k viene dada por el género L de la variedad. Esto se deriva del teorema del índice de Atiyah-Singer aplicado al siguiente operador de firma.

Los paquetes E y F son dados por los +1 y −1 eigenspaces del operador en el paquete de formas diferenciales de X, que actúa sobre k-formas como ${displaystyle i^{k(k-1)}}$ veces el operador estrella Hodge. El operador D es el Hodge Laplacian

{displaystyle Dequiv Delta mathrel {:=} left(mathbf {d} +mathbf {d^{*}} right)^{2}}

restringido a E, donde d es el derivado exterior de Cartan y d* es su adjunto.

El índice analítico de D es la firma de la variedad X, y su índice topológico es el género L de X, por lo que estos son iguales.

Did you mean:

Â genus and Rochlin 's theorem

El género Â es un número racional definido para cualquier variedad, pero en general no es un número entero. Borel y Hirzebruch demostraron que es integral para las variedades de espín, y un entero par si además la dimensión es 4 mod 8. Esto se puede deducir del teorema del índice, que implica que el género Â para las variedades de espín es el índice de una Dirac operador. El factor extra de 2 en dimensiones 4 mod 8 proviene del hecho de que en este caso el kernel y el cokernel del operador de Dirac tienen una estructura cuaterniónica, por lo que como espacios vectoriales complejos tienen dimensiones pares, por lo que el índice es par.

En la dimensión 4, este resultado implica el teorema de Rochlin de que la firma de una variedad de espín de 4 dimensiones es divisible por 16: esto se debe a que en la dimensión 4 el género Â es menos un octavo de la firma.

Técnicas de prueba

Operadores pseudodiferenciales

Los operadores pseudodiferenciales se pueden explicar fácilmente en el caso de operadores de coeficientes constantes en el espacio euclidiano. En este caso, los operadores diferenciales de coeficiente constante son solo las transformadas de Fourier de la multiplicación por polinomios, y los operadores pseudodiferenciales de coeficiente constante son solo las transformadas de Fourier de la multiplicación por funciones más generales.

Muchas demostraciones del teorema del índice utilizan operadores pseudodiferenciales en lugar de operadores diferenciales. La razón de esto es que para muchos propósitos no hay suficientes operadores diferenciales. Por ejemplo, un pseudoinverso de un operador diferencial elíptico de orden positivo no es un operador diferencial, sino un operador pseudodiferencial. Además, existe una correspondencia directa entre los datos que representan elementos de K(B(X), S(X)) (funciones de embrague) y símbolos de operadores pseudodiferenciales elípticos.

Los operadores pseudodiferenciales tienen un orden, que puede ser cualquier número real o incluso −∞, y tienen símbolos (que ya no son polinomios en el espacio cotangente), y los operadores diferenciales elípticos son aquellos cuyos símbolos son invertibles para vectores cotangentes suficientemente grandes. La mayoría de las versiones del teorema del índice se pueden extender de operadores diferenciales elípticos a operadores pseudodiferenciales elípticos.

Cobordismo

La demostración inicial se basó en el teorema de Hirzebruch-Riemann-Roch (1954) e involucró la teoría del cobordismo y los operadores pseudodiferenciales.

La idea de esta primera prueba es más o menos la siguiente. Considere el anillo generado por pares (X, V) donde V es un paquete vectorial suave en la variedad compacta orientada suave X, con relaciones que la suma y el producto del anillo en estos generadores están dados por la unión disjunta y el producto de variedades (con las operaciones obvias en los paquetes vectoriales), y cualquier límite de una variedad con un paquete vectorial es 0. Esto es similar al anillo de cobordismo de variedades orientadas, excepto que las variedades también tienen un paquete vectorial. Los índices topológico y analítico se reinterpretan como funciones de este anillo a los números enteros. Luego se comprueba que estas dos funciones son, de hecho, ambas homomorfismos de anillos. Para probar que son iguales, sólo es necesario comprobar que son iguales en un conjunto de generadores de este anillo. La teoría del cobordismo de Thom da un conjunto de generadores; por ejemplo, espacios vectoriales complejos con el paquete trivial junto con ciertos paquetes sobre esferas de dimensiones pares. Por lo tanto, el teorema del índice se puede probar comprobándolo en estos casos particularmente simples.

Teoría K

La primera prueba publicada de Atiyah y Singer utilizó la teoría K en lugar del cobordismo. Si i es cualquier inclusión de variedades compactas de X a Y, definieron un 'pushforward' operación i_! en operadores elípticos de X a operadores elípticos de Y que conserva el índice. Tomando Y como una esfera en la que se incrusta X, esto reduce el teorema del índice al caso de las esferas. Si Y es una esfera y X es un punto incrustado en Y, entonces cualquier operador elíptico sobre Y es el imagen bajo i_! de algún operador elíptico en el punto. Esto reduce el teorema del índice al caso de un punto, donde es trivial.

Ecuación de calor

Atiyah, Bott y Patodi (1973) ofrecieron una nueva prueba del teorema del índice utilizando la ecuación del calor; véase, p. Berline, Getzler & Verne (1992). La prueba también está publicada en (Melrose 1993) y (Gilkey 1994).

Si D es un operador diferencial con adjunto D*, entonces D*D y DD* son operadores autoadjuntos cuyos valores propios distintos de cero tienen las mismas multiplicidades. Sin embargo, sus espacios propios cero pueden tener diferentes multiplicidades, ya que estas multiplicidades son las dimensiones de los núcleos de D y D*. Por lo tanto, el índice de D viene dado por

{displaystyle operatorname {index} (D)=dim operatorname {Ker} (D^{*})=operatorname {Tr} left(e^{-tD^{*}D}right)-operatorname {Tr} left(e^{-tDD^{*}}right)}

para cualquier t positivo. El lado derecho está dado por la traza de la diferencia de los núcleos de dos operadores de calor. Estos tienen una expansión asintótica para t positivos pequeños, que se pueden usar para evaluar el límite cuando t tiende a 0, dando una prueba del teorema del índice de Atiyah-Singer. Las expansiones asintóticas para t pequeñas parecen muy complicadas, pero la teoría invariante muestra que hay grandes cancelaciones entre los términos, lo que hace posible encontrar explícitamente los términos principales. Estas cancelaciones se explicaron más tarde usando supersimetría.

Más resultados...