Teorema del gráfico cerrado
En matemáticas, el teorema de la gráfica cerrada puede referirse a uno de varios resultados básicos que caracterizan funciones continuas en términos de sus gráficas. Cada uno da condiciones cuando funciones con gráficas cerradas son necesariamente continuas.
Gráficos y mapas con gráficos cerrados
Si es un mapa entre los espacios topológicos entonces Gráfico de es el conjunto o equivalentemente,
Cualquier función continua en un espacio de Hausdorff tiene una gráfica cerrada.
Cualquier mapa lineal, entre dos espacios vectoriales topológicos cuyas topologías son (Cauchy) completas con respecto a la traducción de métricas invariantes, y si además (1a) es secuencialmente continuo en el sentido de la topología del producto, entonces el mapa es continuo y su gráfico, Gr L, está necesariamente cerrado. Por el contrario, si es un mapa lineal con, en lugar de (1a), el gráfico de es (1b) conocido por estar cerrado en el espacio de productos cartesianos , entonces es continua y por lo tanto necesariamente continua.
Ejemplos de mapas continuos que no tienen un gráfico cerrado
Si es cualquier espacio entonces el mapa de identidad es continuo pero su gráfico, que es la diagonal , está cerrado si Es Hausdorff. En particular, si no es Hausdorff entonces es continuo pero sí no tienen un gráfico cerrado.
Vamos denota los números reales con la topología Euclideana habitual y dejar denota con la topología indiscreta (donde note que es no Hausdorff y que cada función valora es continuo). Vamos se define por y para todos . Entonces... es continuo pero su gráfico es no cerrado .
Teorema del grafo cerrado en topología de conjuntos de puntos
En la topología de conjuntos de puntos, el teorema del grafo cerrado establece lo siguiente:
Teorema de gráfico cerrado—Si es un mapa de un espacio topológico en un espacio Hausdorff entonces el gráfico de cerrado si es continuo. El contrario es cierto cuando es compacto. (Nota que la compactidad y la Hausdorffness no implican uno al otro.)
La primera parte es esencialmente por definición.
Segunda parte:
Para cualquier abierto Revisamos está abierto. Así que toma cualquiera construimos un vecindario abierto de tales que .
Desde el gráfico está cerrado, por cada punto en la "línea vertical en x", con dibujar un rectángulo abierto disjoint del gráfico . Estos rectángulos abiertos, cuando se proyectan al eje y, cubren el eje y excepto en así que agrega un conjunto más .
Ingenuamente tratando de tomar construiría un conjunto que contuviera , pero no está garantizado estar abierto, así que utilizamos la compactidad aquí.
Desde es compacto, podemos tomar una cubierta abierta finita como .
Ahora . Es un barrio abierto , ya que es simplemente una intersección finita. Afirmamos que este es el barrio abierto que queremos.
Supongamos que no, entonces hay un poco de mala conducta tales que entonces eso implicaría para algunos por cubierta abierta, pero luego una contradicción ya que se supone que debe ser descompuesto del gráfico .
Los espacios no-Hausdorff rara vez se ven, pero los espacios no-compactos son comunes. Un ejemplo de incumplimiento es la línea real, que permite la función discontinua con gráfico cerrado
Contenido relacionado
La ruina del jugador
Isomorfismo gráfico
Asiento voladizo
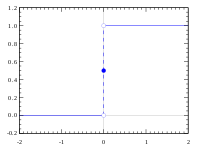

![{displaystyle [-4,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2933acc5278ef7016396bfd3230387904ed5f0f)
![{displaystyle [-2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f94b820404eca2a458cb2c7d8c24be85fffccf90)




































