Teorema de transferencia de potencia máxima

En ingeniería eléctrica, el teorema de máxima transferencia de potencia establece que, para obtener la máxima potencia externa de una fuente de alimentación con resistencia interna, la resistencia de la carga debe ser igual a la resistencia de la fuente vista desde sus terminales de salida. Moritz von Jacobi publicó el teorema de máxima potencia (transferencia) alrededor de 1840; también se conoce como "ley de Jacobi".

El teorema da como resultado una transferencia de potencia máxima desde la fuente de alimentación a la carga, y no una eficiencia máxima de potencia útil a partir de la potencia total consumida. Si la resistencia de la carga se hace mayor que la resistencia de la fuente, entonces la eficiencia aumenta (dado que un porcentaje más alto de la potencia de la fuente se transfiere a la carga), pero la magnitud de la potencia de la carga disminuye (dado que el total aumenta la resistencia del circuito). Si la resistencia de la carga se hace más pequeña que la resistencia de la fuente, la eficiencia disminuye (ya que la mayor parte de la energía termina disipándose en la fuente). Aunque la potencia total disipada aumenta (debido a una menor resistencia total), la cantidad disipada en la carga disminuye.

El teorema establece cómo elegir (para maximizar la transferencia de energía) la resistencia de la carga, una vez que se da la resistencia de la fuente. Es un error común aplicar el teorema en el escenario opuesto. No dice cómo elegir la fuente de resistencia para una determinada resistencia de carga. De hecho, la resistencia de la fuente que maximiza la transferencia de potencia desde una fuente de tensión siempre es cero (la fuente de tensión ideal hipotética), independientemente del valor de la resistencia de la carga.

El teorema se puede extender a los circuitos de corriente alterna que incluyen reactancia y establece que la máxima transferencia de potencia se produce cuando la impedancia de la carga es igual al complejo conjugado de la impedancia de la fuente.

Las matemáticas del teorema también se aplican a otras interacciones físicas, como:

• colisiones mecánicas entre dos objetos,
• el reparto de carga entre dos condensadores,
• flujo líquido entre dos cilindros,
• la transmisión y la reflexión de la luz en el límite entre dos medios.

Maximizar la transferencia de energía frente a la eficiencia energética

Modelo simplificado para alimentar una carga con resistencia R_L por una fuente con tensión V_S y resistencia R_S.

Originalmente, el teorema se malinterpretó (sobre todo por Joule) al implicar que un sistema que consiste en un motor eléctrico accionado por una batería no podría tener más del 50 % de eficiencia, ya que la energía disipada como calor en la batería siempre sería igual a la potencia entregada al motor cuando se emparejaron las impedancias.

En 1880, Edison o su colega Francis Robbins Upton demostraron que esta suposición era falsa y se dieron cuenta de que la máxima eficiencia no era lo mismo que la máxima transferencia de potencia.

Para lograr la máxima eficiencia, la resistencia de la fuente (ya sea una batería o una dinamo) podría (o debería) hacerse lo más cercana posible a cero. Usando esta nueva comprensión, obtuvieron una eficiencia de alrededor del 90 % y demostraron que el motor eléctrico era una alternativa práctica al motor térmico.

La curva roja muestra el poder en la carga, normalizado en relación a su máximo posible. La curva negra muestra la eficiencia ..

La eficiencia η es la relación entre la potencia disipada por la resistencia de carga R_L a la potencia total disipada por el circuito (que incluye la resistencia de la fuente de voltaje de R _S así como R_L):

$${displaystyle eta ={frac {fnMicrom} {L}} {P_{mathrm} {Total} }={frac {I^{2}cdot R_{mathrm {L}}{2}cdot {S}}={frac} {fnMicrom} {L}}{R_{mathrm {L}+R_{mathrm {S}}={frac} {1}{1+R_{mathrm {S}/R_{mathrm.$$

Considere tres casos particulares:

• Si ${displaystyle R_{mathrm {L}/R_{mathrm {S}to 0}$, entonces ${displaystyle eta to 0.}$ La eficiencia se aproxima al 0% si la resistencia a la carga se aproxima a cero (un cortocircuito), ya que toda la energía se consume en la fuente y no se consume energía en el corto. Nota, las fuentes de tensión deben tener alguna resistencia.
• Si ${displaystyle R_{mathrm {L}/R_{mathrm {S}=1}$, entonces ${displaystyle eta ={tfrac {1}{2}}$ La eficiencia es sólo 50% si la resistencia a la carga es igual a la resistencia de la fuente (que es la condición de transferencia de potencia máxima).
• Si ${displaystyle R_{mathrm {L}/R_{mathrm {S}to infty$, entonces ${displaystyle eta to 1.}$ La eficiencia se aproxima al 100% si la resistencia a la carga se acerca al infinito (aunque el nivel total de potencia tiende hacia cero) o si la resistencia a la fuente se aproxima a cero. Usar una gran proporción se llama puente de impedancia.

Coincidencia de impedancia

Un concepto relacionado es la adaptación de impedancia sin reflexión.

En las líneas de transmisión de radiofrecuencia y otros dispositivos electrónicos, a menudo existe el requisito de hacer coincidir la impedancia de la fuente (en el transmisor) con la impedancia de la carga (como una antena) para evitar reflejos en la línea de transmisión que podrían sobrecargar o dañar el transmisor

Prueba basada en cálculo para circuitos puramente resistivos

En el modelo simplificado de alimentar una carga con resistencia R_L por una fuente con voltaje V_S y resistencia de fuente R_S, entonces, según la ley de Ohm, la corriente resultante I es simplemente el voltaje de la fuente dividido por la resistencia total del circuito:

$${displaystyle I={frac {V_{S}{R_{mathrm} {S}+R_{mathrm.$$

La potencia P_L disipada en la carga es el cuadrado de la corriente multiplicado por la resistencia:

$${displaystyle P_{mathrm {L}=I^{2}R_{mathrm {L}=left({frac} {V_{S}{R_{mathrm} {S}+R_{mathrm {L}}}right)}{2}R_{mathrm {L}={frac} {fnMicrom} {fnMicrom} {fnMicrom} {fnMicrom}} {\fn}} {fnK}} {\fn}}}} {fnK}} {fnK}}}} {fnK}}}} {fnK}}}}}}}} {\m} {m}}}}}}}}}}}}} {m} {m}} {m} {m} {m} {s}}} {m} {m} {m}} {m}m}}}}}}}}}}}}}}}}} {m} {m}}} {m} {m} {m}}}}}}}}}} {\s}}}}}}}}}} {m} {m} {m} {s}}}}}}}}}}}}}}}}}} {fnMicrosoft Sans Serif} {fnMicrosoft} {L}+2R_{mathrm {S}+R_{mathrm.$$

El valor de R_L para el cual esta expresión es un máximo podría calcularse diferenciándolo, pero es más fácil calcular el valor de R_L para el cual el denominador

$${displaystyle R_{mathrm {fnMicrosoft Sans Serif} {fnMicrosoft} {L}+2R_{mathrm {S}+R_{mathrm {L}}$$

$${fnMicroc} {dR_{mathrm} {L}}left(R_{mathrm) {fnMicrosoft Sans Serif} {fnMicrosoft} {L}+2R_{mathrm {S}+R_{mathrm {L}right)=-R_{mathrm {fnMicrosoft Sans Serif} {fnMicrosoft} {L} {2}+1.}$$

Para un máximo o mínimo, la primera derivada es cero, entonces

$${displaystyle R_{mathrm {fnMicrosoft Sans Serif} {fnMicrosoft} {L}} {2}=1}$$

$${displaystyle R_{mathrm {L}=pm R_{mathrm {S}.}$$

En circuitos resistivos prácticos, R_S y R< /i>_L son ambos positivos, por lo que el signo positivo de arriba es la solución correcta.

Para saber si esta solución es un mínimo o un máximo, se diferencia nuevamente la expresión del denominador:

$${displaystyle {frac {}{dR_{mathrm} {fnK}}}left({R_{mathrm)}}}left({R_{R_{mathrm} {S} {2}/R_{mathrm} {L}+2R_{mathrm {S}+R_{mathrm {L}}right)={2R_{mathrm {fnK} {fnK} {fnMicrosoft} {fnMicrosoft} {fn}} {fn}}} {fn}} {fn}}}}} {fn}}} {fn}} {\fnK}} {f}}} {fn}}}}}} {\\f}}}}}}}}\\\\\\\\\\\\\\\fn\\\\\\\\\\fn}}}\\fn}}\\\\\fn\\fn\\\fn\\fn\fnfn}\\fn}\\\fn}}}}\\\\fn}}}}}}}}} {L} } {3}}}$$

Esto siempre es positivo para los valores positivos ${displaystyle R_{mathrm {S}$ y ${displaystyle R_{mathrm {L}}$, mostrando que el denominador es un mínimo, y el poder es por lo tanto un máximo, cuando

$${displaystyle R_{mathrm {S}=R_{mathrm {L}.}$$

La prueba anterior asume resistencia a la fuente fija ${displaystyle R_{mathrm {S}$. Cuando la resistencia de la fuente puede ser variada, la energía transferida a la carga se puede aumentar reduciendo ${displaystyle R_{textrm {S}}$. Por ejemplo, una fuente de 100 voltios con una ${displaystyle R_{textrm {S}}$ de ${displaystyle 10,Omega}$ entregará 250 vatios de poder a un ${displaystyle 10,Omega}$ carga; reducción ${displaystyle R_{textrm {S}}$ a ${fnMicrosoft Sans Serif}$ aumenta el poder entregado a 1000 vatios.

Tenga en cuenta que esto muestra que la transferencia de potencia máxima también se puede interpretar como que el voltaje de carga es igual a la mitad del equivalente de voltaje de Thevenin de la fuente.

En circuitos reactivos

El teorema de transferencia de potencia también se aplica cuando la fuente y/o la carga no son puramente resistivas.

Un refinamiento del teorema de la potencia máxima dice que cualquier componente reactivo de la fuente y la carga debe ser de igual magnitud pero de signo opuesto. (Ver abajo para una derivación.)

• Esto significa que la fuente y las impedancias de carga deben ser complejos conjugados uno del otro.
• En el caso de circuitos puramente resistivos, los dos conceptos son idénticos.

Las fuentes y cargas físicamente realizables no suelen ser puramente resistivas, sino que tienen algunos componentes inductivos o capacitivos, por lo que, de hecho, existen aplicaciones prácticas de este teorema, bajo el nombre de adaptación de impedancia conjugada compleja.

Si la fuente es totalmente inductiva (capacitiva), entonces una carga totalmente capacitiva (inductiva), en ausencia de pérdidas resistivas, recibiría el 100 % de la energía de la fuente pero la devolvería después de un cuarto de ciclo.

El circuito resultante no es más que un circuito LC resonante en el que la energía continúa oscilando de un lado a otro. Esta oscilación se llama potencia reactiva.

La corrección del factor de potencia (en la que se usa una reactancia inductiva para "equilibrar" una capacitiva) es esencialmente la misma idea que la adaptación de impedancia conjugada compleja, aunque se realiza por razones completamente diferentes.

Para una fuente reactiva fija, el teorema de potencia máxima maximiza la potencia real (P) entregada a la carga por conjugado complejo que hace coincidir la carga con la fuente.

Para una carga reactiva fija, la corrección del factor de potencia minimiza la potencia aparente (S) (y la corriente innecesaria) conducida por las líneas de transmisión, mientras mantiene la misma cantidad de transferencia de potencia real.

Esto se hace agregando una reactancia a la carga para equilibrar la propia reactancia de la carga, cambiando la impedancia de carga reactiva en una impedancia de carga resistiva.

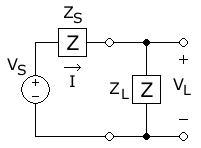
Prueba

En este diagrama, la potencia AC está siendo transferida de la fuente, con la magnitud del fasor de tensión ${displaystyle TENV_{text{S}$ (tensión pico positivo) y impedancia de fuente fija ${displaystyle Z_{text{S}}$ (S para fuente), a una carga con impedancia ${displaystyle Z_{text{L}}$ (L para carga), resultando en una magnitud (positiva) ${displaystyle TENSIA$ del faasor actual ${displaystyle Yo...$. Esta magnitud ${displaystyle TENSIA$ resultados de dividir la magnitud del voltaje fuente por la magnitud de la impedancia total del circuito:

$${displaystyle Новальны={text{S}Principio over TENZ_{text{S}}+Z_{text{L}}$$

El poder promedio ${displaystyle P_{text{L}}$ disipado en la carga es el cuadrado de la corriente multiplicada por la parte resistiva (la parte real) ${displaystyle R_{text{L}}$ de la impedancia de carga ${displaystyle Z_{text{L}}$:

$${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicrosoft} {f}f}}}}f}f} {f}f}f}f}f}f}f}f}f}fnKf}f}fnMicrob}fnKfnKf}f}fnKf}f}fnKfnKf}f}fnKfnKf}f}fnKfnKf}fnKf}fnKfnMicrob}fnKfnKfnKf}}}fnMicro$$

${displaystyle R_{text{S}}$${displaystyle R_{text{L}}$${displaystyle X_{text{S}}$${displaystyle X_{text{L}}$${displaystyle Z_{text{S}}$${displaystyle Z_{text{L}}$

Para determinar, para un voltaje de fuente dado ${displaystyle V_{text{S}}$ y la impedancia ${displaystyle Z_{text{S}}}$ el valor de la impedancia de carga ${displaystyle Z_{text{L}}}$ para el cual esta expresión para el poder produce un máximo, uno primero encuentra, por cada valor positivo fijo de ${displaystyle R_{text{L}}$, el valor del término reactiva ${displaystyle X_{text{L}}$ para el cual el denominador

$${displaystyle (R_{text{S}}+R_{text{L}})^{2}+(X_{text{S}}+X_{text{L}})}{2}}}}$$

$${displaystyle X.$$

Esto reduce la ecuación anterior a:

$${displaystyle P_{text{L}={frac} {1}{2}}{frac {fnfnfnf}}{f} {f}} {f}} {f}}}}}}} {f}}}}}}}}} {f}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$$

${displaystyle R_{text{L}}$${displaystyle R_{text{L}=R_{text{S}}$

Las dos condiciones de maximización

• ${displaystyle ¿Qué?$
• ${displaystyle ¿Qué?$

describir el complejo conjugado de la impedancia fuente, denotado por ${displaystyle ^{*}$ y así se puede combinar concisamente a:

$${displaystyle Z_{text{L}=Z_{S} {*}$$