Teorema de Stokes generalizado

En el cálculo vectorial y la geometría diferencial generalizado Stokes theorem (a veces con apóstrofe como Teorema de Stokes o Teorema de Stokes), también llamado el Stokes-Cartan theorem, es una declaración sobre la integración de formas diferenciales en los múltiples, que tanto simplifica y generaliza varios teoremas del cálculo vectorial. En particular, el teorema fundamental del cálculo es el caso especial donde el múltiple es un segmento de línea, y el teorema de Stokes es el caso de una superficie en ${displaystyle mathbb {R} {} {}}}$. Por lo tanto, el teorema a veces se conoce como el Teorema fundamental del cálculo multivariado.

El teorema de Stokes dice que la parte integral de una forma diferencial ${displaystyle omega }$ sobre el límite ${displaystyle partial Omega }$ de un manifold orientable ${displaystyle Omega }$ es igual a la parte integral de su derivación exterior ${displaystyle domega }$ sobre todo ${displaystyle Omega }$, es decir,

$${displaystyle int _{partial Omega }omega =int _{\ Omega.$$

Stokes' El teorema fue formulado en su forma moderna por Élie Cartan en 1945, siguiendo un trabajo anterior sobre la generalización de los teoremas del cálculo vectorial de Vito Volterra, Édouard Goursat y Henri Poincaré.

Esta moderna forma de teorema de Stokes es una vasta generalización de un resultado clásico que Lord Kelvin comunicó a George Stokes en una carta de fecha 2 de julio de 1850. Stokes puso el teorema como una pregunta sobre el examen del Premio Smith de 1854, lo que llevó al resultado llevando su nombre. Fue publicada por Hermann Hankel en 1861. Este caso clásico relaciona la superficie integral del borde de un campo vectorial ${displaystyle {textbf}}$ sobre una superficie (es decir, el flujo de ${displaystyle {text{curl},{textbf {F}}$) en Euclidean tres espacios a la línea integral del campo vectorial sobre el límite superficial (también conocido como el bucle integral).

Las generalizaciones clásicas del teorema fundamental del cálculo como el teorema de la divergencia y el teorema de Green del cálculo vectorial son casos especiales de la formulación general indicada anteriormente después de hacer una identificación estándar de campos vectoriales con formas diferenciales (diferentes para cada de los teoremas clásicos).

Introducción

El segundo teorema fundamental del cálculo establece que el integral de una función ${displaystyle f}$ sobre el intervalo ${displaystyle [a,b]}$ puede ser calculado por encontrar un antiderivativo ${displaystyle F}$ de ${displaystyle f}$:

$${displaystyle int _{a}^{b}f(x),dx=F(b)-F(a),}$$

Stokes' El teorema es una amplia generalización de este teorema en el siguiente sentido.

• Por la elección de ${displaystyle {textbf}}$, ${displaystyle {frac {dF}=f(x)}$. En la parlanza de formas diferenciales, esto es decir que ${displaystyle f(x),dx}$ es el derivado exterior de la forma 0, es decir, función, ${displaystyle F}$: en otras palabras, que ${displaystyle dF=f,dx}$. El teorema general de Stokes se aplica a formas diferenciales superiores ${displaystyle omega }$ en lugar de sólo 0-formas como ${displaystyle F}$.
• Un intervalo cerrado ${displaystyle [a,b]}$ es un simple ejemplo de un conjunto unidimensional con límite. Su límite es el conjunto que consiste en los dos puntos ${displaystyle a}$ y ${displaystyle b}$. Integración ${displaystyle f}$ a lo largo del intervalo puede ser generalizado para integrar formas en un manifold de dimensiones superiores. Se necesitan dos condiciones técnicas: el múltiple tiene que ser orientable, y la forma debe ser compatible compactamente para dar una integral bien definida.
• Los dos puntos ${displaystyle a}$ y ${displaystyle b}$ forman el límite del intervalo cerrado. Más generalmente, el teorema de Stokes se aplica a los múltiples orientados ${displaystyle M}$ con límite. El límite ${displaystyle partial M}$ de ${displaystyle M}$ es en sí mismo un múltiple y hereda una orientación natural de la de ${displaystyle M}$. Por ejemplo, la orientación natural del intervalo da una orientación de los dos puntos límite. Intuitivamente, ${displaystyle a}$ hereda la orientación opuesta como ${displaystyle b}$, como están en extremos opuestos del intervalo. Así que, "integrando" ${displaystyle F}$ sobre dos puntos límite ${displaystyle a}$, ${displaystyle b}$ está tomando la diferencia ${displaystyle F(b)-F(a)}$.

En términos incluso más simples, uno puede considerar los puntos como límites de curvas, que es como límites 0-dimensionales de múltiples dimensiones. Así, como uno puede encontrar el valor de una integral (${displaystyle f,dx=dF}$) sobre un manifold 1-dimensional (${displaystyle [a,b]}$) considerando el anti-derivativo (${displaystyle F}$) en los límites de 0 dimensiones (${displaystyle {a,b}$), se puede generalizar el teorema fundamental del cálculo, con algunas caveatillas adicionales, para tratar con el valor de las integrales (${displaystyle domega }$) ${displaystyle n}$- manifolds dimensionales (${displaystyle Omega }$) considerando el antiderivativo (${displaystyle omega }$) en el ${displaystyle (n-1)}$- límites dimensionales (${displaystyle partial Omega }$De la manga.

Entonces el teorema fundamental dice:

$${displaystyle int _{[a,b]}f(x),dx=int _{[a,b]},dF=int _{partial ¿Qué? F=F(b)-F(a),}$$

Formulación para variedades suaves con límite

Vamos ${displaystyle Omega }$ ser un andamio liso orientado con límite de dimensión ${displaystyle n}$ y dejar ${displaystyle alpha }$ ser un liso ${displaystyle n}$- forma diferencial que es compatible compactamente ${displaystyle Omega }$. Primero, supongamos que ${displaystyle alpha }$ es compatible compactamente en el dominio de un único gráfico de coordenadas orientado ${displaystyle {U,varphi}}$. En este caso, definimos la integral de ${displaystyle alpha }$ sobre ${displaystyle Omega }$ como

$${displaystyle int _{ Omega }alpha =int _{varphi (U)}(varphi ^{-1})^{*}alpha ,}$$

${displaystyle alpha }$

${displaystyle mathbb {R} {} {}} {fn}}$

Más generalmente, la integral de ${displaystyle alpha }$ sobre ${displaystyle Omega }$ se define como sigue: Vamos ${displaystyle {psi _{i}}}$ ser una partición de unidad asociada con una cubierta localmente finita ${displaystyle {U_{i},varphi ¿Qué?$ de (consistentemente orientado) tablas de coordenadas, luego definir la integral

$${displaystyle int _{ Omega ¿Qué? Alpha,$$

${displaystyle mathbb {R} {} {}} {fn}}$

El teorema de Stokes generalizado dice:

Theorem()Stokes-Cartan)—Vamos ${displaystyle omega }$ ser un liso ${displaystyle (n-1)}$-forma con soporte compacto en una orientación, ${displaystyle n}$- manifold-with-boundary ${displaystyle M}$, donde ${displaystyle partial M}$ se da la orientación inducida. Entonces...

$${displaystyle int _{M}domega =int _{partial M}omega.}$$

Aquí. ${displaystyle d}$ es el derivado exterior, que se define utilizando la estructura múltiple solamente. El lado derecho se escribe a veces como ${textstyle oint _{partial Omega }omega }$ el hecho de que ${displaystyle (n-1)}$- Manifold ${displaystyle partial Omega }$ no tiene límite. (Este hecho es también una implicación del teorema de Stokes, ya que para un dado suave ${displaystyle n}$- manifold dimensional ${displaystyle Omega }$, aplicación del teorema dos veces da ${textstyle int _{partial (partial Omega)}omega =int _{Omega }d(domega)=0}$ para cualquier ${displaystyle (n-2)}$-forme ${displaystyle omega }$, lo que implica que ${displaystyle partial (partial Omega)=emptyset }$.) El lado derecho de la ecuación se utiliza a menudo para formular integral leyes; el lado izquierdo entonces conduce a equivalentes diferencial formulaciones (véase infra).

El teorema se utiliza a menudo en situaciones donde ${displaystyle Omega }$ es un submanifold de orientación empotrada de un gran manifold, a menudo ${displaystyle mathbb {R} {cH00}$, en la cual la forma ${displaystyle omega }$ se define.

Preliminares topológicos; integración sobre cadenas

Sea M una variedad suave. Un k-simplex singular (suave) en M se define como un mapa suave del simplex estándar en R^k a M . El grupo C_k(M, Z) de k cadenas singulares en M se define como el grupo abeliano libre en el conjunto de singulares k-simples en < span class="texhtml mvar" style="font-style:italic;">M. Estos grupos, junto con el mapa de límites, ∂, definen un complejo de cadenas. El grupo de homología correspondiente (resp. cohomología) es isomorfo al grupo de homología singular habitual H_k(< i>M, Z) (resp. el grupo de cohomología singular H ^k(M, Z)), definido usando simples simples continuos en lugar de suaves en M.

Por otro lado, las formas diferenciales, con derivación exterior, d, como el mapa de conexión, forman un complejo de cochain, que define los grupos de cohomología de Rham ${displaystyle ¿Qué?$.

Las k-formas diferenciales se pueden integrar en un k-simplex de forma natural, retrocediendo a R^k. La extensión por linealidad permite integrar sobre cadenas. Esto proporciona un mapa lineal desde el espacio de las formas k hasta las formas késimo grupo de cochains singulares, C^k(M, Z), los funcionales lineales en C_k(M, Z). En otras palabras, una forma k ω define un funcional

$${displaystyle I(omega)(c)=oint ¿Qué?$$

kddual∂

1. formas cerradas, es decir, dω = 0, tener cero integral sobre límites, es decir, sobre los múltiples que se pueden escribir como ∂_c M_c, y
2. formas exactas, es decir, ⋅ = dσ, tener cero integral sobre ciclos, es decir, si los límites se suman al conjunto vacío: ._c M_c = ∅.

El teorema de De Rham muestra que este homomorfismo es de hecho un isomorfismo. Entonces, lo contrario a 1 y 2 arriba es cierto. En otras palabras, si {c_i} son ciclos que generan el késimo grupo de homología, luego para cualquier número real correspondiente, {a_i} , existe una forma cerrada, ω, tal que

$${displaystyle oint ###{c_{i}omega =a_{i},}$$

Stokes' El teorema de las variedades suaves se puede derivar de Stokes' teorema para cadenas en variedades suaves y viceversa. Dicho formalmente, este último dice:

Theorem()Teorema de Stokes para cadenas)—Si c es un liso k- Encadenado en un suave manifold M, y ⋅ es un liso ()k −1)-forme sobre M, entonces

$${displaystyle int _{partial c}omega =int - {c}domega.}$$

Principio subyacente

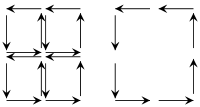
Para simplificar estos argumentos topológicos, vale la pena examinar el principio subyacente considerando un ejemplo para d = 2 dimensiones. La idea esencial puede entenderse por el diagrama de la izquierda, que muestra que, en un mosaico orientado de una variedad, los caminos interiores se recorren en direcciones opuestas; sus contribuciones a la integral de trayectoria se anulan por pares. Como consecuencia, solo queda la contribución del límite. Por lo tanto, basta con demostrar que Stokes' teorema para teselaciones suficientemente finas (o, de manera equivalente, simples), que por lo general no es difícil.

Ejemplo de análisis vectorial clásico

Vamos ${displaystyle gamma:[a,b]to mathbb {R} ^{2}$ Sé una curva de plano suave Jordan. El teorema curva Jordan implica que ${displaystyle gamma }$ divideciones ${displaystyle mathbb {R} {2}}$ en dos componentes, uno compacto y otro que no es completo. Vamos ${displaystyle D}$ denota la parte compacta que está sujeta ${displaystyle gamma }$ y supongan ${displaystyle psi:Dto mathbb [R] ^{3}$ es suave, con ${displaystyle S=psi (D)}$. Si ${displaystyle "Gamma"$ es la curva espacial definida por ${displaystyle Gamma (t)=psi (gamma (t)}$ y ${displaystyle {textbf}}$ es un campo vectorial suave en ${displaystyle mathbb {R} {} {}}}$, entonces:

$${displaystyle oint _{ Gamma }mathbf {F} ,cdot ,d{mathbf {nabla times mathbf {F} right)cdot ,dmathbf {S}$$

Esta declaración clásica, es un caso especial de la formulación general después de hacer una identificación de un campo vectorial con una forma de 1 y su rotacional con una forma de dos a través

$${fnK}cdot} DGammato F_{x},dx+F_{y},dy+F_{z},dz}$$

$${displaystyle {begin{aligned} {nabla times {begin{pmatrix}F_{x}F_{y}\F_{z}end{pmatrix}cdot dmathbf {S} ={begin{pmatrix}partial ¿Por qué? ¿Por qué? ¿Por qué? ¿Por qué? ¿Por qué? {y}F_{x}\end{pmatrix}cdot dmathbf {S} to \[1.4ex] limitd(F_{x},dx+F_{y},dy+F_{z},dz)=left(partial) ¿Por qué? ¿Por qué? _{z}F_{x}-partial _{x}F_{z}right)dzwedge dx+left(partial) ¿Por qué? - Sí.$$

Generalización a conjuntos aproximados

Una región (aquí se llama D en lugar de Ω) con el borde liso delgado. Este es un manifold con esquinas, por lo que su límite no es un manifold suave.

La formulación anterior, en la que ${displaystyle Omega }$ es un manifold suave con límite, no basta en muchas aplicaciones. Por ejemplo, si el dominio de la integración se define como la región plana entre dos ${displaystyle x}$-coordina y los gráficos de dos funciones, a menudo sucederá que el dominio tiene esquinas. En tal caso, los puntos de esquina significan que ${displaystyle Omega }$ no es un conjunto suave con el límite, y por lo tanto la declaración del teorema de Stokes dada arriba no se aplica. Sin embargo, es posible comprobar que la conclusión del teorema de Stokes sigue siendo verdadera. Esto es porque ${displaystyle Omega }$ y su límite están bien abiertos lejos de un pequeño conjunto de puntos (un conjunto de medida cero).

Una versión del teorema de Stokes que permite la rugosidad fue probada por Whitney. Supongamos que ${displaystyle D}$ es un subconjunto abierto conectado ${displaystyle mathbb {R} {} {}} {fn}}$. Call ${displaystyle D}$ a dominio estándar si satisface la siguiente propiedad: existe un subconjunto ${displaystyle P}$ de ${displaystyle partial D}$, abre ${displaystyle partial D}$, cuyo complemento ${displaystyle partial D}$ tiene Hausdorff ${displaystyle (n-1)}$- Medida cero; y tal que cada punto de ${displaystyle P}$ tiene vector normal generalizado. Esto es un vector ${displaystyle {textbf}(x)}$ tal que, si se elige un sistema de coordenadas, ${displaystyle {textbf}(x)}$ es el vector de primera base, entonces, en un vecindario abierto alrededor ${displaystyle x}$, existe una función suave ${displaystyle f(x_{2},dotsx_{n}}$ tales que ${displaystyle P}$ es el gráfico ${displaystyle {x_{1}=f(x_{2},dotsx_{n}}}}$ y ${displaystyle D}$ es la región ${displaystyle {x_{1}:x_{1}cantadof(x_{2},dotsx_{n}}}}$. Whitney comenta que el límite de un dominio estándar es la unión de un conjunto de cero Hausdorff ${displaystyle (n-1)}$-medida y una unión finita o contable de lisa ${displaystyle (n-1)}$- Manifolds, cada uno de los cuales tiene el dominio en un solo lado. Él entonces prueba eso si ${displaystyle D}$ es un dominio estándar en ${displaystyle mathbb {R} {} {}} {fn}}$, ${displaystyle omega }$ es un ${displaystyle (n-1)}$-forma que se define, continua y atada ${displaystyle Dcup P}$, suave en ${displaystyle D}$, integrado en ${displaystyle P}$, y tal que ${displaystyle domega }$ es integrado en ${displaystyle D}$, entonces el teorema de Stokes sostiene, es decir,

$${displaystyle int _{P}omega =int ¿Qué?$$

El estudio de las propiedades teóricas de la medida de los conjuntos aproximados conduce a la teoría de la medida geométrica. Incluso versiones más generales de Stokes' teorema han sido probados por Federer y por Harrison.

Casos especiales

La forma general del teorema de Stokes usando formas diferenciales es más poderosa y fácil de usar que los casos especiales. Las versiones tradicionales se pueden formular utilizando coordenadas cartesianas sin la maquinaria de la geometría diferencial y, por lo tanto, son más accesibles. Además, son mayores y, como resultado, sus nombres son más familiares. Los científicos e ingenieros a menudo consideran que las formas tradicionales son más convenientes, pero la falta de naturalidad de la formulación tradicional se vuelve evidente cuando se usan otros sistemas de coordenadas, incluso los familiares como las coordenadas esféricas o cilíndricas. Existe la posibilidad de confusión en la forma en que se aplican los nombres y el uso de formulaciones duales.

Caso clásico (cálculo vectorial)

Una ilustración del teorema de Stokes vectorial-calculus, con superficie ${displaystyle Sigma }$, su límite ${displaystyle partial Sigma }$ y el vector "normal" n.

Este es un caso (dualizado) (1 + 1) dimensional, para un formulario de 1 (dualizado porque es una afirmación sobre campos vectoriales). Este caso especial a menudo se denomina simplemente Stokes' teorema en muchos cursos universitarios de introducción al cálculo vectorial y se utiliza en física e ingeniería. También se conoce a veces como el teorema curl.

El teorema clásico de Stokes relaciona la superficie integral del borde de un campo vectorial sobre una superficie ${displaystyle Sigma }$ en Euclidean tres espacios a la línea integral del campo vectorial sobre su límite. Es un caso especial del teorema general de Stokes (con ${displaystyle n=2}$) una vez identificamos un campo vectorial con una forma 1 usando la métrica en Euclidean 3-espacio. La curva de la línea integral, ${displaystyle partial Sigma }$, debe tener orientación positiva, lo que significa que ${displaystyle partial Sigma }$ puntos en sentido contrario cuando la superficie normal, ${displaystyle n}$, puntos hacia el espectador.

Una consecuencia de este teorema es que las líneas de campo de un campo vectorial con rotacional cero no pueden ser contornos cerrados. La fórmula se puede reescribir como:

Theorem—Suppose ${displaystyle {textbf}={big (}P(x,y,z),Q(x,y,z),R(x,y,z){big)}$ se define en una región con superficie lisa ${displaystyle Sigma }$ y tiene derivados parciales de primer orden continuos. Entonces...

$${displaystyle iint _{ Sigma. Y... z}-{frac {partial R}{partial x}right)dz,dx+left({frac {partial Q}{partial Q}{partial x}-{frac {partial P}{partial y}}right)dx,dy{Biggr)}=oint _{partial Sigma }{Big (}P,dx+Q,dy+R,dz{Big)},}}$$

Donde ${displaystyle P,Q}$ y ${displaystyle R.$ son los componentes ${displaystyle {textbf}}$, y ${displaystyle partial Sigma }$ es el límite de la región ${displaystyle Sigma }$.

Teorema de Green

El teorema de Green se reconoce inmediatamente como el tercer integrando de ambos lados de la integral en términos de P, Q y R antes citada.

En electromagnetismo

Dos de las cuatro ecuaciones de Maxwell involucran rotaciones de campos vectoriales tridimensionales, y sus formas diferenciales e integrales están relacionadas por el caso especial tridimensional (cálculo vectorial) de Stokes' teorema. Se debe tener cuidado para evitar casos con límites móviles: las derivadas de tiempo parcial están destinadas a excluir tales casos. Si se incluyen los límites móviles, el intercambio de integración y diferenciación introduce términos relacionados con el movimiento de los límites que no se incluyen en los resultados a continuación (ver Diferenciación bajo el signo integral):

Nombre	Forma diferencial	Forma integral (usando tridimensional) Stokes theorem plus relativistic invariance, ${displaystyle textstyle int {tfrac {partial }{partial t}dots to {tfrac {d} {dt}textstyle int cdots }$)
Ecuación de Maxwell-Faraday Ley de inducción de Faraday:	${displaystyle nabla times mathbf {E} =-{frac {partial mathbf {B}{partial t}}$	${displaystyle {begin{aligned}oint ¿Qué? {E} cdot dmathbf {l}=iint _{S}nabla times mathbf {E} cdot dmathbf {A} \fn_iint _{S}{frac {partial mathbf {B} {f}cdot dmathbf {A}end{aligned}}}$ (con C y S no necesariamente fijos)
Ley de Ampère (con la extensión de Maxwell):	${displaystyle nabla times mathbf {H} =mathbf {J} +{frac {partial mathbf {} {fn} {fn}} {fn}} {fn}} {fn}}} {fn}}}}} {fn}}}}}} {fn}}}}}}} {fn}}}}}}} {f}}}}}}}}}}}}}} {$	${displaystyle {begin{aligned}oint ♪♪Mathbf {H} cdot dmathbf {l} &=iint _{S}nabla times mathbf {H} cdot dmathbf {A}\\iint _{S}mathbf {cdot dmathbf {A} +iint _{S}{frac {partial mathbf {D} {fn}cdot dmathbf {A} end{aligned}}$ (con C y S no necesariamente fijos)

El subconjunto mencionado anteriormente de las ecuaciones de Maxwell es válido para campos electromagnéticos expresados en unidades SI. En otros sistemas de unidades, como CGS o unidades gaussianas, los factores de escala para los términos difieren. Por ejemplo, en unidades gaussianas, la ley de inducción de Faraday y la ley de Ampère toman las formas:

$${displaystyle {begin{aligned}nabla times mathbf {E}=-{frac} {1}{c}{frac {partial mathbf {B}{partial t}\,\\nabla times mathbf {f} {f} {f} {f}} {f}f} {f}} {f}} {f}} {f} {f} {f}f}f}f}f}f}f} {f} {f}f} {f}f}\f}f}f}f}f}f}f}f}f}f}f}f}f}f}\f}f}f}\\f}f}f}f}f}f}f}\\\f}f}f}f}f}f}f}f}f}f}f}\\\f}f}f}f}f}f}f}f}f}f}f}\f}\\f}fn {D} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fn}}} {fnMicrosoft}}} {fnMicrosoft}}} {f}}} {fnMicrosoft}}}}} {fnMicrosoft}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\fnMicrom}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { t}+{frac {4pi} }Mathbf {J} ,end{aligned}$$

c

Teorema de la divergencia

Del mismo modo, el teorema de la divergencia

$${displaystyle int _{mathrm {Vol}nabla cdot mathbf {F} ,d_{mathrm {Vol}=oint _{partial operatorname {Vol} 'Mathbf {F} cdot d{boldsymbol {Sigma }$$

${displaystyle (n-1)}$${displaystyle {textbf}=f{vec} {c}}$${displaystyle {vec}}$

$${displaystyle {vec {}cdot int _{mathrm {Vol}nabla f,d_{mathrm {Vol}={vec} {c}cdot oint _{partial mathrm {Vol} }f,d{boldsymbol {Sigma},}$$

${displaystyle {vec}}$

$${displaystyle int _{mathrm {Vol}nabla f,d_{mathrm {Vol} }=oint _{partial mathrm {Vol} }f,d{boldsymbol {Sigma},}$$

Integral de volumen del gradiente del campo escalar

Vamos ${displaystyle f: Omega to mathbb {R}$ ser un campo de escalar. Entonces...

$${displaystyle int _{ Omega... {fn}$$

${displaystyle {vec}}$${displaystyle partial Omega }$

Prueba: Vamos ${displaystyle {vec}}$ ser un vector. Entonces...

$${displaystyle {begin{aligned}0 limit=int ¿Qué? {fn}cdot {fn}cdot {c}f}{text{by the divergence theorem}\\\nt=int ¿Qué? Omega... "Omega" {f}cdot {vecn}f\\cccccccc} {c}cdot int _{ Omega }f-{vec {c}cdot int _{partial ################################################################################################################################################################################################################################################################ {c}cdot left(int _{ Omega.$$

${displaystyle {vec}}$