Teorema de separación de hiperplanos

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En geometría, el teorema de separación de hiperplanos es un teorema sobre conjuntos convexos disjuntos en un espacio euclidiano de n-dimensional. Existen varias versiones bastante similares. En una versión del teorema, si ambos conjuntos son cerrados y al menos uno de ellos es compacto, entonces hay un hiperplano entre ellos e incluso dos hiperplanos paralelos entre ellos separados por un espacio. En otra versión, si ambos conjuntos convexos disjuntos son abiertos, entonces hay un hiperplano entre ellos, pero no necesariamente un espacio. Un eje que es ortogonal a un hiperplano separador es un eje separador, porque las proyecciones ortogonales de los cuerpos convexos sobre el eje son disjuntas.

El teorema de separación de hiperplanos se debe a Hermann Minkowski. El teorema de separación de Hahn-Banach generaliza el resultado a espacios vectoriales topológicos.

Un resultado relacionado es el teorema del hiperplano de apoyo.

En el contexto de las máquinas de vectores de soporte, el hiperplano de separación óptima o hiperplano de margen máximo es un hiperplano que separa dos capas convexas de puntos y es equidistante de las dos.

Declaraciones y pruebas

Teorema de separación hiperplano — Vamos. $A$ y $B$ ser dos subconjuntos convexos descomunados de $\mathbb {R} {} {}} {\fn}$ . Entonces existe un vector no cero $v$ y un número real $c$ tales que

\langle x,v\rangle \geq c\,{\text{ and }\langle y,v\rangle \leq c

para todos $x$ dentro $A$ y $y$ dentro $B$ ; es decir, el hiperplano $\langle \cdotv\rangle =c$ , $v$ el vector normal, separa $A$ y $B$ .

Si ambos conjuntos están cerrados, y al menos uno de ellos es compacto, entonces la separación puede ser estricta, es decir, ${\displaystyle \langle x,v\rangle œc_{1}\,{\text{ and }\langle y,v\rangle - No.$ para algunos $c_{1} {2$

En todos los casos, asuma $A,B$ para ser descompuestos, no vacíos, y subconvexos de $\mathbb {R} {} {}} {\fn}$ . El resumen de los resultados es el siguiente:

Resumen
$A$	$B$	$\langle x,v\rangle$	$\langle y,v\rangle$
		$\geq c$	$\leq c$
compacto cerrado	cerrado	$>c_{1}$	${\displaystyle - No.$ con $c_{2$
cerrado	compacto cerrado	$>c_{1}$	${\displaystyle - No.$ con $c_{2$
abierto		$>c$	$\leq c$
abierto	abierto	$>c$	${\displaystyle]$

El número de dimensiones debe ser finito. En espacios de dimensión infinita hay ejemplos de dos conjuntos cerrados, convexos y disjuntos que no pueden separarse mediante un hiperplano cerrado (un hiperplano donde una función lineal continua es igual a alguna constante) incluso en el sentido débil donde las desigualdades no son estrictas.

Aquí, la compacidad de la hipótesis no se puede relajar; véase un ejemplo en la sección Contraejemplos y unicidad. Esta versión del teorema de separación se generaliza a dimensiones infinitas; la generalización se conoce más comúnmente como el teorema de separación de Hahn-Banach.

La prueba se basa en el siguiente lema:

Lemma — Vamos. $A$ y $B$ ser dos subconjuntos cerrados de $\mathbb {R} {} {}} {\fn}$ , y asumir $A$ es compacto. Entonces existen puntos $a_{0}\in A$ y $b_{0}\in B$ minimizando la distancia ${\fnuncio$ sobre $a\in A$ y $b\in B$ .

Prueba de la lema

Vamos. $a\in A$ y $b\in B$ ser cualquier par de puntos, y dejar $R_{1}=\fnción-a\fnción$ . Desde $A$ es compacto, está contenido en una bola centrada en $a$ ; que el radio de esta bola sea $R_{2$ . Vamos. $S=B\cap {\fnMicroline {B_{1}+r_{2}(a)}$ ser la intersección de $B$ con una bola cerrada de radio $r_{1}+r_{2$ alrededor $a$ . Entonces... ${\displaystyle S.$ es compacto y no vacío porque contiene $b$ . Puesto que la función de distancia es continua, existen puntos $A_{0$ y $B_{0$ cuya distancia ${\displaystyle "Perfecto"$ es el mínimo sobre todos los pares de puntos en $A\times S$ . Queda por demostrar que $A_{0$ y $B_{0$ de hecho tienen la distancia mínima sobre todos los pares de puntos en $A\times B$ . Supongamos por contradicción que existen puntos $a'$ y $b'$ tales que ${\fnK}\fnK}\fnK$ . Entonces en particular, ${} {\fnK}$ , y por la desigualdad del triángulo, $\ sufrimientoa-b'\ eterna\leq\ eternaa'-b'\ impermea-a'\ eternaa'a'\ obedecidor_{1}+r_{2}$ . Por lo tanto $b'$ figura en ${\displaystyle S.$ , que contradice el hecho de que $A_{0$ y $B_{0$ tenía una distancia mínima $A\times S$ . $\square$

Prueba de teorema

Primero demostramos el segundo caso. (Vea el diagrama.)

WLOG, $A$ es compacto. Por la lema, existen puntos $a_{0}\in A$ y $b_{0}\in B$ de mínima distancia entre sí. Desde $A$ y $B$ están deshonrados, tenemos $a_{0}\neq B_{0$ . Ahora, construir dos hiperplanos $L_{A},L_{B$ perpendicular a segmento de línea $[a_{0},b_{0$ Con $L_{A$ enfrente $A_{0$ y $L_{B$ enfrente $B_{0$ . Afirmamos que tampoco $A$ ni $B$ entra en el espacio entre $L_{A},L_{B$ , y así los hiperplanos perpendiculares a $(a_{0},b_{0}$ satisfacer el requisito del teorema.

Algebraicamente, los hiperplanos $L_{A},L_{B$ son definidos por el vector $v:=b_{0}-a_{0$ y dos constantes ${\displaystyle C_{A}:=\langle v,a_{0}\rangle - No.$ , tal que $L_{A}=\{x:\langle v,x\rangle =c_{A},L_{B}=\{x:\langle v,x\rangle =c_{B}\$ . Nuestra afirmación es que $\forall a\in A,\langle v,a\rangle \leq c_{A$ y $\forall b\in B,\langle v,b\rangle \geq c_{B$ .

Supongamos que hay algunos $a\in A$ tales que $\langle v,a\rangle œc_{A$ , entonces deja $a'$ ser el pie de perpendicular desde $B_{0$ al segmento de línea ${\displaystyle [a_{0},a]$ . Desde $A$ es convexo, $a'$ Está dentro. $A$ , y por geometría plano, $a'$ está más cerca $B_{0$ que $A_{0$ , contradicción. El argumento similar se aplica a $B$ .

Ahora para el primer caso.

Enfoque ambos $A,B$ desde el interior $A_{1}\subseteq A_{2}\subseteq \cdots \subseteq A$ y $B_{1}\subseteq B_{2}\subseteq \cdots \subseteq B$ , tal que cada $A_{k},B_{k$ es cerrado y compacto, y los sindicatos son los interiores relativos $\mathrm {relint} (A),\mathrm {relint} (B)$ . (Ver página relativa interior para detalles.)

Ahora por el segundo caso, por cada par $A_{k},B_{k$ existe una unidad vectorial $V_{k$ y número real $C_{k$ , tal que ${\displaystyle \langle v_{k},A_{k}\rangle ¿Qué?$ .

Puesto que la esfera de unidad es compacta, podemos tomar una subsequencia convergente, de modo que $v_{k}\to v$ . Vamos. ${\displaystyle c_{A}:=\sup _{a\in A}\langle v,a\ranglec_{B}:=\inf _{b\in B}\langle v,b\rangle$ . Afirmamos que ${\displaystyle C_{A}\leq C.$ , separando así $A,B$ .

Supongamos que no, entonces hay algunos $a\in A,b\in B$ tales que $\langle v,a\rangle$ entonces desde $v_{k}\to v$ , por lo suficientemente grande $k$ , tenemos $\langle v_{k},a\rangle }\langle v_{k},b\rangle$ , contradicción.

Dado que un hiperplano separador no puede intersecar los interiores de conjuntos convexos abiertos, tenemos un corolario:

Teorema de separación I — Vamos. $A$ y $B$ ser dos conjuntos de convexos no vacíos. Si $A$ está abierto, entonces existe un vector no cero $v$ y número real $c$ tales que

\langle x,v\rangle œc\,{\text{ and }\langle y,v\rangle \leq c

para todos $x$ dentro $A$ y $y$ dentro $B$ . Si ambos conjuntos están abiertos, entonces existe un vector no cero $v$ y número real $c$ tales que

{\displaystyle \langle x,v\rangle >c\,{\text{ and }\langle y,v\rangle

para todos $x$ dentro $A$ y $y$ dentro $B$ .

Caso con posibles intersecciones

Si los sets $A,B$ tienen posibles intersecciones, pero sus interiores relativos están descompuestos, entonces la prueba del primer caso todavía se aplica sin cambio, dando así:

Teorema de separación II — Vamos. $A$ y $B$ ser dos subconjuntos convexos no vacíos de $\mathbb {R} {} {}} {\fn}$ con interiores relativos descomunales. Entonces existe un vector no cero $v$ y un número real $c$ tales que

\langle x,v\rangle \geq c\,{\text{ and }\langle y,v\rangle \leq c

En particular, tenemos el teorema del hiperplano que lo sustenta.

Apoyo al teorema de hiperplano — si $A$ es un convexo establecido en $\mathbb {R} ^{n$ y $A_{0$ es un punto en el límite $A$ , entonces existe un hiperplano de apoyo $A$ que contiene $A_{0$ .

Prueba

Si la afinidad de la $A$ no es todo $\mathbb {R} {} {}} {\fn}$ , luego extender el ataúd a un hiperplano de apoyo. Else, $\mathrm {relint} (A)=\mathrm {int} (A)$ está descompuesto $\mathrm {relint} (\{a_{0})=\{a_{0}$ Así que aplica el teorema anterior.

Converso de teorema

Obsérvese que la existencia de un hiperplano que sólo "separa" dos conjuntos convexos en el sentido débil de que ambas desigualdades no son estrictas obviamente no implica que los dos conjuntos sean disjuntos. Ambos conjuntos podrían tener puntos ubicados en el hiperplano.

Contraexampos y singularidad

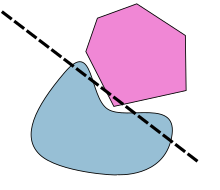
Si uno de los dos, A o B, no es convexo, entonces hay muchos contraejemplos posibles. Por ejemplo, A y B podrían ser círculos concéntricos. Un contraejemplo más sutil es aquel en el que A y B son ambos cerrados pero ninguno es compacto. Por ejemplo, si A es un semiplano cerrado y B está limitado por un brazo de una hipérbola, entonces no hay ningún hiperplano estrictamente separador:

A=\{(x,y):x\leq 0

B=\{(x,y):x confianza0,y\geq 1/x\

(Aunque, por una instancia del segundo teorema, existe un hiperplano que separa sus interiores.) Otro tipo de contraejemplo tiene a A compacto y a B abierto. Por ejemplo, A puede ser un cuadrado cerrado y B puede ser un cuadrado abierto que toca a A.

En la primera versión del teorema, evidentemente el hiperplano separador nunca es único. En la segunda versión, puede ser único o no. Técnicamente, un eje separador nunca es único porque puede trasladarse; en la segunda versión del teorema, un eje separador puede ser único hasta la traslación.

El ángulo del cuerno proporciona un buen contraejemplo a muchas separaciones de hiperplano. Por ejemplo, en $\mathbb {R} {2}$ , el disco de unidad está descompuesto desde el intervalo abierto $((1,0),(1,1)$ , pero la única línea que los separa contiene la totalidad de $((1,0),(1,1)$ . Esto demuestra que si $A$ está cerrado y $B$ es relativamente relativamente abierto, entonces no existe necesariamente una separación que es estricta para $B$ . Sin embargo, si $A$ cerrado politopo entonces existe tal separación.

Más variantes

El lema de Farkas y los resultados relacionados pueden entenderse como teoremas de separación de hiperplanos cuando los cuerpos convexos están definidos por un número finito de desigualdades lineales.

Se pueden encontrar más resultados.

Uso en detección de colisión

En la detección de colisiones, el teorema de separación de hiperplanos se suele utilizar de la siguiente forma:

Teorema de eje separador — Dos objetos convexos cerrados se descomponen si existe una línea ("axis separador") en la que las proyecciones de los dos objetos se descomponen.

Independientemente de la dimensionalidad, el eje de separación es siempre una línea. Por ejemplo, en 3D, el espacio está separado por planos, pero el eje de separación es perpendicular al plano de separación.

El teorema del eje de separación se puede aplicar para la detección rápida de colisiones entre mallas poligonales. La dirección normal u otra característica de cada cara se utiliza como eje de separación. Tenga en cuenta que esto produce posibles ejes de separación, no líneas o planos de separación.

En 3D, el uso exclusivo de las normales de las caras no logrará separar algunos casos de bordes que no colisionan. Se requieren ejes adicionales, que consisten en los productos cruzados de pares de bordes, uno tomado de cada objeto.

Para lograr una mayor eficiencia, los ejes paralelos pueden calcularse como un solo eje.

Véase también

Doble cono
Lemma de Farkas
Teorema de Kirchberger
Control óptimo

Notas

^ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). Elementos del aprendizaje estadístico: minería de datos, inferencia y predicción (PDF) (Segunda edición). Nueva York: Springer. pp. 129–135.
^ Witten, Ian H.; Frank, Eibe; Hall, Mark A.; Pal, Christopher J. (2016). Data Mining: Practice Machine Learning Tools and Techniques (Cuarta edición). Morgan Kaufmann. págs. 253 a 254. ISBN 9780128043578.
^ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Matemáticas para el aprendizaje automático. Cambridge University Press. pp. 337–338. ISBN 978-1-108-45514-5.
^ Boyd " Vandenberghe 2004, Ejercicio 2.22.
^ Haïm Brezis, Analyse fonctionnelle: théorie et applications, 1983, remarque 4, p. 7.
^ a b Stoer, Josef; Witzgall, Christoph (1970). Convexidad y optimización en Dimensiones Finitas I. Springer Berlin, Heidelberg. (2.12.9). doi:10.1007/978-3-642-46216-0. ISBN 978-3-642-46216-0.
^ "Mata avanzada vectorial".

Referencias

Boyd, Stephen P.; Vandenberghe, Lieven (2004). Optimización de Convex (PDF). Cambridge University Press. ISBN 978-0-521-83378-3.
Golshtein, E. G.; Tretyakov, N.V. (1996). Mapas Modificados de Lagrangians y monotone en optimización. Nueva York: Wiley. p. 6. ISBN 0-471-54821-9.
Shimizu, Kiyotaka; Ishizuka, Yo; Bard, Jonathan F. (1997). Programación matemática de dos niveles. Boston: Kluwer Academic Publishers. p. 19. ISBN 0-7923-9821-1.

Soltan, V. (2021). Propiedades de soporte y separación de conjuntos convexo en dimensión finita. Extracta Math. Vol. 36, no. 2, 241-278.

Enlaces externos

Detección y respuesta de colisión

Análisis funcional (tópico – glosario)

Espacios

Banach Besov Fréchet Hilbert Hölder Nuclear Orlicz Schwartz Sobolev vector topológico
Propiedades	Barrelled Completa Dual (Algebraic/Topological) Localmente convex Reflexivo Separables

Teoremas

Hahn-Banach
Representación de Riesz
Gráfico cerrado
Principio de fijación uniforme
Punto fijo de Kakutani
Krein-Milman
Min-max
Gelfand-Naimark
Banach – Alaoglu

Operadores

Adjoint
Librada
Compacto
Hilbert - Schmidt
Normal
Nuclear
Clase de rastreo
Transpose
Sin límites
Unitario

Álgebras

Banach álgebra
C*-algebra
Espectro de un álgebra C*
Álgebra Operadora
Álgebra de grupo de un grupo localmente compacto
Von Neumann álgebra

Problemas abiertos

Problema subespacial invariable
Conjetura de Mahler

Aplicaciones

Espacio difícil
Teoría espectral de ecuaciones diferenciales ordinarias
núcleo de calor
Teorema de índice
Cálculo de variaciones
Cálculo funcional
Operador integral
Jones polynomial
Teoría de campo cuántico Topológica
Geometría no recíproca
Hipótesis Riemann
Distribución (o funciones generales)

Temas avanzados

Bienes aproximados
Conjunto equilibrado
Teoría del ramo
Topología débil
Banach – Distancia mazur
Tomita–Teoría de Takesaki

Categoría

v t e Espacios vectoriales topológicos (TVSs)
Conceptos básicos	Banach space Completeness Operador lineal continuo Funcional lineal Espacio Fréchet Mapa lineal Localmente espacio convexo Metrizability Operator topologies Espacio vectorial topológico Espacio vectorial
Principales resultados	Anderson-Kadec Banach – Alaoglu Teorema de gráfico cerrado F. Riesz Hahn-Banach (separación de Hyperplane Hahn-Banach valorado en vectores Cartografía abierta (Banach-Schauder) Herido inverso Armonización uniforme (Banach-Steinhaus)
Mapas	Operador bilinario forma Mapa lineal Casi abierto Librada Continua Cerrado Compacto Definido de forma negativa Distinua Homomorfismo Topológico Funcional Linear Bilinear Sesquilinear Norm Seminorm Función sublineal Transpose
Tipos de conjuntos	Absolutamente convex/disk Absorbing/Radial Affine Equilibrado/Circulo Discos de banach Puntos de encuentro Librada Subespacio complementario Convex Convex cone (subset) Cono lineal (subset) Punto extremo Pre-compacto/Totalmente atado Prevalente/shy Radial Convexo radical/en forma de estrella Simétrica
Establecer operaciones	Affine hull (Relativo) Interior algebraico (core) Convex hull Lapso lineal Minkowski adición Polar (Quasi) Interior relativo
Tipos de TVS	Asplund B-completo/Ptak Banach Barrelled BK-space (Ultra-) Bornological Brauner Completa Conveniente (DF)-space Distinguidos F-espacio Espacio FK-AK FK-space Fréchet tame Fréchet Grothendieck Hilbert Infrabarreled Espacio de interpolación K-space LB-space LF-space Localmente espacio convexo Mackey (Pseudo) Montel Quasibarrelled Cuasi-completo Quasinormed (Polynomially) Semi-) Reflexivo Riesz Schwartz Semi-complete Smith Estereotipo (B) Strictly Uniformemente) convex (Quasi-) Ultrabarrelled Uniformemente suave Webbed Con la propiedad de aproximación
Categoría

Más resultados...