Teorema de noether

noters se usa en la física teórica y el cálculo de las variaciones. Revela la relación fundamental entre las simetrías de un sistema físico y las leyes de conservación. También hizo que los físicos teóricos modernos se centraron mucho más en las simetrías de los sistemas físicos. Una generalización de las formulaciones sobre constantes de movimiento en la mecánica lagrangiana y hamiltoniana (desarrollada en 1788 y 1833, respectivamente), no se aplica a los sistemas que no pueden modelarse solo con un lagrangiano (por ejemplo, sistemas con una función de disipación de Rayleigh). En particular, los sistemas disipativos con simetrías continuas no necesitan tener una ley de conservación correspondiente.

Ilustraciones básicas y antecedentes

Como ilustración, si un sistema físico se comporta lo mismo independientemente de cómo esté orientado en el espacio (es decir, es invariante), su lagrangiano es simétrico bajo rotación continua: a partir de esta simetría, noéter ' El teorema dicta que se conserva el momento angular del sistema, como consecuencia de sus leyes de movimiento. El sistema físico en sí no necesita ser simétrico; Un asteroide irregular en el espacio conserva el momento angular a pesar de su asimetría. Son las leyes de su movimiento las que son simétricas.

Como otro ejemplo, si un proceso físico exhibe los mismos resultados, independientemente del lugar o el tiempo, entonces su lagrangiano es simétrico bajo traducciones continuas en el espacio y el tiempo respectivamente: por el teorema de Noether, estas simetrías explican las leyes de conservación de impulso lineal y energía dentro de este sistema, respectivamente.

El teorema de Noether es importante, tanto por la visión que da a las leyes de conservación, como también como una herramienta de cálculo práctica. Permite a los investigadores determinar las cantidades conservadas (invariantes) de las simetrías observadas de un sistema físico. Por el contrario, permite a los investigadores considerar clases completas de lagrangianos hipotéticos con invariantes dados, para describir un sistema físico. Como ilustración, supongamos que se propone una teoría física que conserva una cantidad x . Un investigador puede calcular los tipos de lagrangianos que conservan x a través de una simetría continua. Debido al teorema de Noether, las propiedades de estos lagrangianos proporcionan criterios adicionales para comprender las implicaciones y juzgar la aptitud de la nueva teoría. El teorema de Noether está tan bien incorporado en Qft que:

"...cualquier resultado que parezca romper que el teorema se puede declarar inmediatamente como ocultar un error calculado."

lo que le permite actuar como un modelo matemático para gran parte de la investigación contemporánea en física.

Existen numerosas versiones del teorema de Noether, con diversos grados de generalidad. Hay contrapartes cuánticas naturales de este teorema, expresadas en las identidades Ward-Takahashi. También existen generalizaciones del teorema de Noether a superespacios.

Enunciado informal del teorema

Dejando de lado todos los detalles técnicos, el teorema de Noether se puede enunciar de manera informal:

Si un sistema tiene una propiedad de simetría continua, entonces hay cantidades correspondientes cuyos valores se conservan en el tiempo.

Una versión más sofisticada del teorema que involucra campos establece que:

A cada simetría diferenciable generada por acciones locales corresponde una corriente conservada.

La palabra " simetría " En la declaración anterior, se refiere más precisamente a la covarianza de la forma que una ley física toma con respecto a un grupo de transformaciones de Lie unidimensional que satisface ciertos criterios técnicos. La ley de conservación de una cantidad física generalmente se expresa como una ecuación de continuidad.

La prueba formal del teorema utiliza la condición de invariancia para derivar una expresión para una corriente asociada con una cantidad física conservada. En la terminología moderna (desde c. 1980), la cantidad conservada se llama la carga noter , mientras que el flujo que transporta esa carga se llama la corriente noter . La corriente de noéter se define hasta un campo vectorial solenoidal (sin divergencia).

En el contexto de la gravitación, la declaración de Felix Klein de NoTher, el teorema de no se estipula a la acción i para los invariantes:

Si una integral I es invariante bajo un grupo continuo G_*** con *** parámetros, entonces *** combinaciones linealmente independientes de las expresiones lagrangianas son divergencias.

Breve ilustración y descripción general del concepto

Parcela ilustrativa Teorema de Noether para una simetría en sentido de coordenadas.

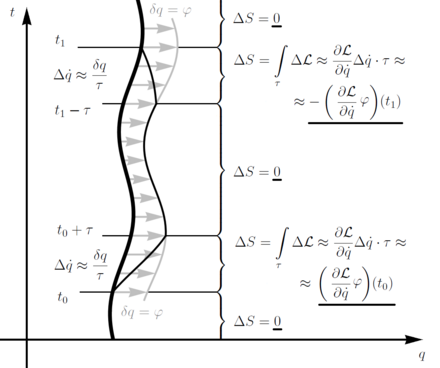
La idea principal detrás del teorema de Noether es más fácilmente ilustrada por un sistema con una coordenadas q{displaystyle q} y una simetría continua φ φ :q↦ ↦ q+δ δ q{displaystyle varphi:qmapsto q+delta q} (flechas grises en el diagrama). Considere cualquier trayectoria q()t){displaystyle q(t)} (bold en el diagrama) que satisface las leyes del sistema de movimiento. Es decir, la acción S{displaystyle S. gobernar este sistema es estacionario en esta trayectoria, es decir, no cambia bajo ninguna variación local de la trayectoria. En particular, no cambiaría bajo una variación que aplica el flujo de simetría φ φ {displaystyle varphi } en un segmento de tiempo [t₀, t₁] y es inmóvil fuera de ese segmento. Para mantener la trayectoria continua, utilizamos períodos de "compasión" de tiempo pequeño τ τ {displaystyle tau } a la transición entre los segmentos gradualmente.

El cambio total en la acción S{displaystyle S. ahora comprende cambios traídos por cada intervalo en juego. Partes, donde la variación misma desaparece, no traen Δ Δ S{displaystyle Delta S}. La parte media tampoco cambia la acción, porque su transformación φ φ {displaystyle varphi } es una simetría y así preserva el Lagrangian L{displaystyle L. y la acción S=∫ ∫ L{textstyle S=int L}. Las únicas partes que quedan son las piezas "buffering". Roughly speaking, they contribute mostly through their "slanting" qÍ Í → → qÍ Í ± ± δ δ q/τ τ {displaystyle { dot {fnK}derecho { dot {q}pm delta q/tau }.

Eso cambia el Lagrangiano por Δ Δ L.. ()∂ ∂ L/∂ ∂ qÍ Í )Δ Δ qÍ Í {displaystyle Delta Lapprox {bigl (}partial L/partial {dot {q}{bigr)} Delta., que se integra en

Δ Δ S=∫ ∫ Δ Δ L.. ∫ ∫ ∂ ∂ L∂ ∂ qÍ Í Δ Δ qÍ Í .. ∫ ∫ ∂ ∂ L∂ ∂ qÍ Í ()± ± δ δ qτ τ ).. ± ± ∂ ∂ L∂ ∂ qÍ Í δ δ q=± ± ∂ ∂ L∂ ∂ qÍ Í φ φ .{displaystyle Delta S=int Delta Lapprox int {frac {partial L}{partial {dot {q}}} Delta {dot {}approx int {frac {partial L}{dot { dot {}}}left(pm {delta q}{tau }right)approx pm {frac {partial L}{dot { dot}}}} {det}} {det}} {det}}} {det}}}}det}}}det}}det}det {det {det {det}}} {d}}}}d}}}}}d}}}}}ddddddddd}dd}d}d}d}dddddddd}d}d}d}d}d}d}d}d}d}dd}d}d}d q=pm {frac {partial l}varphi.}

Estos últimos términos, evaluados alrededor de los puntos finales t0{displaystyle T_{0} y t1{displaystyle T_{1}, debe cancelarse el uno al otro para hacer el cambio total en la acción Δ Δ S{displaystyle Delta S} ser cero, como se esperaría si la trayectoria es una solución. Eso es

()∂ ∂ L∂ ∂ qÍ Í φ φ )()t0)=()∂ ∂ L∂ ∂ qÍ Í φ φ )()t1),{displaystyle left({frac {partial L}{dot {}}varphi right)(t_{0})=left({frac {partial L}{dot {dot {}}}}varphi right)(t_{1}}}}}}} {d]

()∂ ∂ L/∂ ∂ qÍ Í )φ φ {displaystyle left(partial L/partial {dot {q}right)varphi }

q{displaystyle q}

()∂ ∂ L/∂ ∂ qÍ Í )=p{displaystyle left(partial L/partial {dot {q}right)=p}

Los casos más generales siguen la misma idea:

Contexto histórico

Una ley de conservación establece que alguna cantidad X en la descripción matemática de la evolución de un sistema permanece constante a lo largo de su movimiento: es un invariante. Matemáticamente, la tasa de cambio de X (su derivada con respecto al tiempo) es cero,

dXdt=XÍ Í =0.{displaystyle {frac {dX}{dt}={dot {X}=0~}

Se dice que tales cantidades se conservan; a menudo se denominan constantes de movimiento (aunque no es necesario que se trate del movimiento per se, solo de la evolución en el tiempo). Por ejemplo, si la energía de un sistema se conserva, su energía es invariable en todo momento, lo que impone una restricción al movimiento del sistema y puede ayudar a resolverlo. Además de los conocimientos que tales constantes de movimiento brindan sobre la naturaleza de un sistema, son una herramienta de cálculo útil; por ejemplo, una solución aproximada se puede corregir encontrando el estado más cercano que satisfaga las leyes de conservación adecuadas.

Las primeras constantes de movimiento descubiertas fueron la cantidad de movimiento y la energía cinética, propuestas en el siglo XVII por René Descartes y Gottfried Leibniz sobre la base de experimentos de colisión, y refinadas por investigadores posteriores. Isaac Newton fue el primero en enunciar la conservación de la cantidad de movimiento en su forma moderna y demostró que era una consecuencia de la tercera ley de Newton. De acuerdo con la relatividad general, las leyes de conservación del momento lineal, la energía y el momento angular solo son exactamente verdaderas globalmente cuando se expresan en términos de la suma del tensor de tensión-energía (tensión-energía no gravitacional) y la tensión-energía de Landau-Lifshitz. –pseudotensor de momento (energía-esfuerzo gravitacional). La conservación local del momento y la energía lineales no gravitacionales en un sistema de referencia de caída libre se expresa mediante la desaparición de la divergencia covariante del tensor tensión-energía. Otra importante cantidad conservada, descubierta en estudios de la mecánica celeste de los cuerpos astronómicos, es el vector de Laplace-Runge-Lenz.

A finales del siglo XVIII y principios del XIX, los físicos desarrollaron métodos más sistemáticos para descubrir invariantes. Un gran avance se produjo en 1788 con el desarrollo de la mecánica lagrangiana, que está relacionada con el principio de mínima acción. En este enfoque, el estado del sistema se puede describir mediante cualquier tipo de coordenadas generalizadas q; las leyes del movimiento no necesitan expresarse en un sistema de coordenadas cartesianas, como era habitual en la mecánica newtoniana. La acción se define como la integral de tiempo I de una función conocida como lagrangiana L

I=∫ ∫ L()q,qÍ Í ,t)dt,{displaystyle I=int L(mathbf {q}{dot {Mathbf {q} }, t),dt~,}

donde el punto sobre q representa la tasa de cambio de las coordenadas q,

qÍ Í =dqdt.{fnMicrosoft Sans Serif} }={frac {dmathbf {q} - Sí.

El principio de Hamilton establece que el camino físico q(t), el que realmente toma el sistema, es un camino para el cual las variaciones infinitesimales en ese path no causa ningún cambio en I, al menos hasta el primer orden. Este principio da como resultado las ecuaciones de Euler-Lagrange,

ddt()∂ ∂ L∂ ∂ qÍ Í )=∂ ∂ L∂ ∂ q.{displaystyle {frac {d}left({frac {partial L}{dot {mathbf {}}}}}}}right)={frac {partial L}{mathbf {}}}}}}}}}}}}right)={frac {partial L}{Mathbf {}}}}}}}}}}}}}}}}}}}}}}}}}}} { }~

Por lo tanto, si una de las coordenadas, digamos q_k, no aparece en el Lagrangiano, el lado derecho de la ecuación es cero y el lado izquierdo -lado de la mano requiere que

ddt()∂ ∂ L∂ ∂ qÍ Í k)=dpkdt=0,{displaystyle {frac {d}dt}left({frac {partial L}{dot {}_{k}}}}}right)={frac {dp_{k} {dt}=0~,}

donde el impulso

pk=∂ ∂ L∂ ∂ qÍ Í k{displaystyle {fnK}= {fnMicroc {fnMicrosoft} {fnMicrosoft {f} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft {f}f}fnMicroc} {f}fnMicroc}f} {f}f}f}f}f}f}f}f}\f}f}f}f}f}f}f}f}f}f}f}f}\f}f}f}f}\\\\\f}fnhfnf}fn}\\\\\fn\fnh}f}f}f}fn}fnh}\\\\\\fnh}\f}fn {fnK}}

se conserva durante todo el movimiento (en el camino físico).

Por lo tanto, la ausencia de la coordenada ignorable q_k del Lagrangiano implica que el Lagrangiano no se ve afectado por cambios o transformaciones de q_k; el lagrangiano es invariante y se dice que exhibe una simetría bajo tales transformaciones. Esta es la idea semilla generalizada en el teorema de Noether.

En el siglo XIX se desarrollaron varios métodos alternativos para encontrar cantidades conservadas, especialmente por William Rowan Hamilton. Por ejemplo, desarrolló una teoría de transformaciones canónicas que permitía cambiar las coordenadas para que algunas coordenadas desaparecieran del Lagrangiano, como se indicó anteriormente, lo que resultó en momentos canónicos conservados. Otro enfoque, y quizás el más eficiente para encontrar cantidades conservadas, es la ecuación de Hamilton-Jacobi.

Expresión matemática

Forma simple usando perturbaciones

La esencia del teorema de Noether es generalizar la noción de coordenadas ignorables.

Se puede suponer que el lagrangiano L definido anteriormente es invariante bajo pequeñas perturbaciones (alabeos) de la variable de tiempo t y las coordenadas generalizadas q. Uno puede escribir

t→ → t.. =t+δ δ tq→ → q.. =q+δ δ q,{displaystyle {begin{aligned}t ventajarightarrow t^{prime }=t+delta t\\mathbf {q} > Rightarrow mathbf {q} ^{prime }=mathbf {q} #

donde las perturbaciones δt y δq son pequeñas, pero variables. Para generalizar, suponga que hay (digamos) N tales transformaciones de simetría de la acción, es decir, transformaciones que dejan la acción sin cambios; etiquetado por un índice r = 1, 2, 3,..., N.

Entonces, la perturbación resultante se puede escribir como una suma lineal de los tipos individuales de perturbaciones,

δ δ t=.. rε ε rTrδ δ q=.. rε ε rQr,{displaystyle {begin{aligned}delta t _{r}varepsilon ¿Qué? {q} - ¿Qué? ♪♪Mathbf {Q} {fn} {fnMicrosoft}}

donde ε_r son los coeficientes infinitesimales de los parámetros correspondientes a cada uno:

• generador T_r de la evolución del tiempo, y
• generador Q_r de las coordenadas generalizadas.

Para traducciones, Q_r es una constante con unidades de longitud; para rotaciones, es una expresión lineal en las componentes de q, y los parámetros forman un ángulo.

Usando estas definiciones, Noether demostró que las cantidades N

()∂ ∂ L∂ ∂ qÍ Í ⋅ ⋅ qÍ Í − − L)Tr− − ∂ ∂ L∂ ∂ qÍ Í ⋅ ⋅ Qr{displaystyle left({frac {partial L}{partial {dot {mathbf {}}}}}}cdot {dot {mathbf {cH0}}}}} {cdot {cdot { dot { dot {cH0}} {cH0} {fnK}}cdot mathbf {fnK}

se conservan (constantes de movimiento).

Ejemplos

Yo. Invariancia temporal

Para ilustrar, considere un Lagrangiano que no depende del tiempo, es decir, que es invariante (simétrico) bajo cambios t → t + δt, sin ningún cambio en las coordenadas q. En este caso, N = 1, T = 1 y Q = 0; la cantidad conservada correspondiente es la energía total H

H=∂ ∂ L∂ ∂ qÍ Í ⋅ ⋅ qÍ Í − − L.{displaystyle H={frac {partial L}{dot {f}}cdot {f}cdot { dot {mthbf {f} - Sí.

II. Invariancia traslacional

Considere un Lagrangiano que no depende de una coordenada q_k ("ignorable", como arriba); entonces es invariante (simétrico) bajo cambios q_k → q_k + δq_k. En ese caso, N = 1, T = 0 y Q_k = 1; la cantidad conservada es el momento lineal correspondiente p_k

pk=∂ ∂ L∂ ∂ qkÍ Í .{displaystyle {fnK}}}

En relatividad especial y general, estas dos leyes de conservación pueden expresarse globalmente (como se hizo arriba) o localmente como una ecuación de continuidad. Las versiones globales se pueden unir en una sola ley de conservación global: la conservación del 4-vector de energía-momento. Las versiones locales de la conservación de la energía y la cantidad de movimiento (en cualquier punto del espacio-tiempo) también se pueden unir en la conservación de una cantidad definida localmente en el punto del espacio-tiempo: el tensor de tensión-energía (esto se derivará en la siguiente sección).

III. Invariancia rotacional

La conservación del momento angular L = r × p es análoga a su homólogo del momento lineal. Se supone que la simetría del Lagrangiano es rotacional, es decir, que el Lagrangiano no depende de la orientación absoluta del sistema físico en el espacio. Para concretar, suponga que el Lagrangiano no cambia bajo pequeñas rotaciones de un ángulo δθ alrededor de un eje n; tal rotación transforma las coordenadas cartesianas por la ecuación

r→ → r+δ δ Silencio Silencio n× × r.{displaystyle mathbf {r} rightarrow mathbf {r} +delta theta ,mathbf {n} times mathbf {r}

Dado que el tiempo no se está transformando, T = 0, y N = 1. Tomando δθ como el ε y las coordenadas cartesianas r como las coordenadas generalizadas q, las correspondientes variables Q vienen dadas por

Q=n× × r.{displaystyle mathbf {Q} =mathbf {n} times mathbf {r}

Entonces el teorema de Noether establece que la siguiente cantidad se conserva,

∂ ∂ L∂ ∂ qÍ Í ⋅ ⋅ Q=p⋅ ⋅ ()n× × r)=n⋅ ⋅ ()r× × p)=n⋅ ⋅ L.{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} {fnh}cdotcdotcdotcdotcdotmathbf {Q}=mathbf {p} cdot left(mathbf { n} times mathbf {r}=mathbf {n} {cdot} {cdot} {cdot} {L}.}

En otras palabras, se conserva la componente del momento angular L a lo largo del eje n. Y si n es arbitrario, es decir, si el sistema es insensible a cualquier rotación, entonces todos los componentes de L se conservan; en resumen, el momento angular se conserva.

Versión de teoría de campos

Aunque útil por derecho propio, la versión del teorema de Noether que se acaba de dar es un caso especial de la versión general derivada en 1915. Para dar una idea del teorema general, una versión del teorema de Noether Ahora se da el teorema para campos continuos en el espacio-tiempo de cuatro dimensiones. Dado que los problemas de la teoría de campos son más comunes en la física moderna que los problemas de mecánica, esta versión de la teoría de campos es la versión más utilizada (o implementada con mayor frecuencia) del teorema de Noether.

Que haya un conjunto de campos diferentes φ φ {displaystyle varphi } definida sobre todo espacio y tiempo; por ejemplo, la temperatura T()x,t){displaystyle T(mathbf {x}t)} sería representativo de tal campo, siendo un número definido en cada lugar y hora. El principio de la menor acción puede aplicarse a esas esferas, pero la acción es ahora una parte integral del espacio y del tiempo

S=∫ ∫ L()φ φ ,∂ ∂ μ μ φ φ ,xμ μ )d4x{displaystyle {mathcal {S}=in {fnMithcal}left(varphipartial _{mu} }varphix^{mu }derecha),d^{4}x}

(el teorema se puede generalizar aún más al caso en el que el lagrangiano depende de la n^ésima derivada, y también se puede formular usando haces jet).

Una transformación continua de los campos φ φ {displaystyle varphi } puede ser escrito infinitamente como

φ φ ↦ ↦ φ φ +ε ε Ψ Ψ ,{displaystyle varphi mapsto varphi + 'varepsilon Psi}

Donde Ψ Ψ {displaystyle Psi } es en general una función que puede depender de ambos xμ μ {displaystyle x^{mu}} y φ φ {displaystyle varphi }. La condición para Ψ Ψ {displaystyle Psi } para generar una simetría física es que la acción S{displaystyle {fnMithcal}} queda invariable. Esto ciertamente será cierto si la densidad lagrangiana L{displaystyle {fnMithcal}} se deja invariable, pero también será verdad si el Lagrangiano cambia por una divergencia,

L↦ ↦ L+ε ε ∂ ∂ μ μ ▪ ▪ μ μ ,{displaystyle {fnMitcal {fnMicrosoft Sans Serif} {cHFF}+varepsilon partial _{mu Lambda ^{mu }

ya que la parte integral de una divergencia se convierte en un término límite según el teorema de divergencia. Un sistema descrito por una acción dada podría tener múltiples simetrías independientes de este tipo, indexadas por r=1,2,...... ,N,{displaystyle r=1,2,ldotsN,} para que la transformación más general de la simetría sea escrita como

φ φ ↦ ↦ φ φ +ε ε rΨ Ψ r,{displaystyle varphi mapsto varphi + 'varepsilon ¿Qué?

con la consecuencia

L↦ ↦ L+ε ε r∂ ∂ μ μ ▪ ▪ rμ μ .{displaystyle {fnMitcal {fnMicrosoft Sans Serif} {fnMitcal {}+varepsilon ¿Por qué? Lambda... }

Para esos sistemas, El teorema de Noether afirma que hay N{displaystyle N} conservadas densidades actuales

jr.. =▪ ▪ r.. − − ∂ ∂ L∂ ∂ φ φ ,.. ⋅ ⋅ Ψ Ψ r{displaystyle J. Lambda... }-{frac {partial {fnMitcal {} {fnMitcal {fnMicrosoft Sans Serif}cdot Psi _{r}}}

(donde se entiende que el producto de puntos contrata el sobre el terreno índices, no los .. {displaystyle nu } índice o índice r{displaystyle r} índice).

En tales casos, la ley de conservación se expresa en forma de cuatro dimensiones

∂ ∂ .. j.. =0,{displaystyle partial _{nu }j^{nu }=0,}

que expresa la idea de que la cantidad de una cantidad conservada dentro de una esfera no puede cambiar a menos que parte de ella fluya fuera de la esfera. Por ejemplo, la carga eléctrica se conserva; la cantidad de carga dentro de una esfera no puede cambiar a menos que parte de la carga salga de la esfera.

Para ilustrar, considere un sistema físico de campos que se comporta lo mismo en las traducciones en tiempo y espacio, como se consideró anteriormente; en otras palabras, L()φ φ ,∂ ∂ μ μ φ φ ,xμ μ ){displaystyle Lleft({boldsymbol {varphi }}partial _{mu }{boldsymbol {varphi }},x^{mu }right)} es constante en su tercer argumento. En ese caso, N= 4, uno para cada dimensión del espacio y del tiempo. Una traducción infinitesimal en el espacio, xμ μ ↦ ↦ xμ μ +ε ε rδ δ rμ μ {displaystyle x^{mu}mapsto x^{mu }+varepsilon ¿Por qué? ¿Qué? (con δ δ {displaystyle delta } denotar el Kronecker delta), afecta los campos como φ φ ()xμ μ )↦ ↦ φ φ ()xμ μ − − ε ε rδ δ rμ μ ){displaystyle varphi (x^{mu })mapsto varphi left(x^{mu }-varepsilon _ {r}delta _{r} {mu }right)}: es decir, reetiquetar las coordenadas es equivalente a dejar las coordenadas en su lugar al traducir el campo mismo, que a su vez es equivalente a transformar el campo sustituyendo su valor en cada punto xμ μ {displaystyle x^{mu}} con el valor en el punto xμ μ − − ε ε Xμ μ {displaystyle x^{mfnMicrosoft} }- 'varepsilon X^{mu} "detrás" que sería mapeado xμ μ {displaystyle x^{mu}} por el desplazamiento infinitesimal bajo consideración. Puesto que esto es infinitesimal, podemos escribir esta transformación como

Ψ Ψ r=− − δ δ rμ μ ∂ ∂ μ μ φ φ .{displaystyle Psi _{r}=-delta ¿Qué? }partial _{mu Álvaro.

La densidad lagrangiana se transforma de la misma manera, L()xμ μ )↦ ↦ L()xμ μ − − ε ε rδ δ rμ μ ){displaystyle {mathcal {}left(x^{mu }right)mapsto {fnMitcal {}left(x^{mu} }-varepsilon _ {r}delta _{r} {mu }right)}Así que

▪ ▪ rμ μ =− − δ δ rμ μ L{displaystyle Lambda _{}{mu} }=-delta ¿Qué? # {fnMitcal {L}}

y así El teorema de Noether corresponde a la ley de conservación para el tensor de estrés – energía T_μ^., donde hemos usado μ μ {displaystyle mu } en lugar de r{displaystyle r}. Es decir, usando la expresión dada anteriormente, y coleccionando las cuatro corrientes conservadas (una para cada μ μ {displaystyle mu }) en un tensor T{displaystyle T}El teorema de Noether da

Tμ μ .. =− − δ δ μ μ .. L+δ δ μ μ σ σ ∂ ∂ σ σ φ φ ∂ ∂ L∂ ∂ φ φ ,.. =()∂ ∂ L∂ ∂ φ φ ,.. )⋅ ⋅ φ φ ,μ μ − − δ δ μ μ .. L{displaystyle - ¿Qué? }=-delta _{mu. # {fnMitcal {L}+delta _{mu}. ##partial _{sigma } varphi {frac {partial {mathcal {} {partial varphi _{,nu }}=left {frac {partial {mathcal {}}{partial varphi _{,nu }}}}}}}cdot varphi _{,mu }demu }demu # {fnMitcal {L}}

con

Tμ μ .. ,.. =0{displaystyle - ¿Qué? } {fnMicrosoft Sans Serif}

(rebeldemos) μ μ {displaystyle mu } como σ σ {displaystyle sigma } en un paso intermedio para evitar conflictos). (Sin embargo, el T{displaystyle T} obtenido de esta manera puede diferir del tensor simétrico utilizado como el término fuente en la relatividad general; ver el estrés canónico – tensor de energía.)

La conservación de la carga eléctrica, por el contrario, se puede derivar considerando Ψ lineal en los campos φ en lugar de en las derivadas. En mecánica cuántica, la amplitud de probabilidad ψ(x) de encontrar una partícula en un punto x es un campo complejo φ, porque atribuye un número complejo a cada punto en el espacio y el tiempo. La amplitud de probabilidad en sí misma es físicamente inmedible; solo la probabilidad p = |ψ|² puede inferirse de un conjunto de medidas. Por lo tanto, el sistema es invariante bajo transformaciones del campo ψ y su campo complejo conjugado ψ^* que dejan |ψ|² sin cambios, como

↑ ↑ → → eiSilencio Silencio ↑ ↑ ,↑ ↑ Alternativa Alternativa → → e− − iSilencio Silencio ↑ ↑ Alternativa Alternativa ,{displaystyle psi rightarrow e^{itheta }psi \psi ^{*}rightarrow e^{-itheta }psi ^{*}~}

una rotación compleja. En el límite cuando la fase θ se vuelve infinitesimalmente pequeña, δθ, puede tomarse como parámetro ε, mientras que el Ψ son iguales a iψ y −iψ*, respectivamente. Un ejemplo específico es la ecuación de Klein-Gordon, la versión relativistamente correcta de la ecuación de Schrödinger para partículas sin espín, que tiene la densidad lagrangiana

L=∂ ∂ .. ↑ ↑ ∂ ∂ μ μ ↑ ↑ Alternativa Alternativa .. .. μ μ +m2↑ ↑ ↑ ↑ Alternativa Alternativa .{displaystyle L=partial _{nu }psi partial _{mu }psi ^{*}eta ^{nu mu }+m^{2}psi psi ^{*}

En este caso, el teorema de Noether establece que la corriente conservada (∂ ⋅ j = 0) es igual a

j.. =i()∂ ∂ ↑ ↑ ∂ ∂ xμ μ ↑ ↑ Alternativa Alternativa − − ∂ ∂ ↑ ↑ Alternativa Alternativa ∂ ∂ xμ μ ↑ ↑ ).. .. μ μ ,{displaystyle j^{nu }=ileft({frac {partial psi }{partial x^{mu }}psi ^{*}frac {partial psi ^{*}{partial x^{mu }}}psi right)eta ^{nu mu }~}

que, cuando se multiplica por la carga de esa especie de partícula, es igual a la densidad de corriente eléctrica debida a ese tipo de partícula. Esta "invariancia de calibre" fue observado por primera vez por Hermann Weyl, y es uno de los prototipos de simetría de calibre de la física.

Derivaciones

Una variable independiente

Considere el caso más simple, un sistema con una variable independiente, el tiempo. Suponga que las variables dependientes q son tales que la integral de acción

I=∫ ∫ t1t2L[q[t],qÍ Í [t],t]dt{displaystyle I=int ¿Qué?

es invariante ante breves variaciones infinitesimales en las variables dependientes. En otras palabras, satisfacen las ecuaciones de Euler-Lagrange

ddt∂ ∂ L∂ ∂ qÍ Í [t]=∂ ∂ L∂ ∂ q[t].{fnMicrosoft} {fnK} {fnMicrosoft} {fnMicrosoft} {cH} {f}}} {fn}} {fn}fnK} {fnK}}} {f}}}}}} {fn}}}}}}fnf}}} {f}f}f}f}}}}}}}f}}}}}}f}}}}}}}\f}f}f}\\f}fn\fnK}}}fn\\\\\f}}}\fnKfnMicrob}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {b}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} [t]={frac {partial L}{partial mathbf {q}[t].}

Y suponga que la integral es invariante bajo una simetría continua. Matemáticamente, tal simetría se representa como un flujo, φ, que actúa sobre las variables de la siguiente manera

t→ → t.=t+ε ε Tq[t]→ → q.[t.]=φ φ [q[t],ε ε ]=φ φ [q[t.− − ε ε T],ε ε ]{displaystyle {begin{aligned}t ventajarightarrow t'=t+varepsilon T\Mathbf {q} [t] golperightarrow mathbf {q} '[t]=varphi [mathbf {q} [t],varepsilon ]=varphi [mathbf {q} [t'-varepsilon T],varepsilon]end{aligned}

donde ε es una variable real que indica la cantidad de flujo, y T es una constante real (que podría ser cero) que indica cuánto cambia el flujo en el tiempo.

qÍ Í [t]→ → qÍ Í .[t.]=ddtφ φ [q[t],ε ε ]=∂ ∂ φ φ ∂ ∂ q[q[t.− − ε ε T],ε ε ]qÍ Í [t.− − ε ε T].{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {cHFF} {cHFF} {cH00}} {fnMicroc {} {f}}varphi} [mathbf {q} [t],varepsilon]={frac {partial varphi }{partial mathbf {q}} {Mathbf {q} [t'-varepsilon T],varepsilon]{dot {mathbf {q} }[t'-varepsilon T].}

La integral de acción fluye hacia

I.[ε ε ]=∫ ∫ t1+ε ε Tt2+ε ε TL[q.[t.],qÍ Í .[t.],t.]dt.=∫ ∫ t1+ε ε Tt2+ε ε TL[φ φ [q[t.− − ε ε T],ε ε ],∂ ∂ φ φ ∂ ∂ q[q[t.− − ε ε T],ε ε ]qÍ Í [t.− − ε ε T],t.]dt.{displaystyle {begin{aligned}I'[varepsilon] _{t_{1}+varepsilon T}{t_{2}+varepsilon T}L[mathbf {q} '[t],{dot {mathbf {q}' {t',t'],dt '[6pt] _{t_{1}+varepsilon T}{t_{2}+varepsilon L[varphi] [Mathbf {q} [t'-varepsilon T],varepsilon ],{frac {partial varphi }{partial mathbf {q}} {Mathbf {q} [t'-varepsilon T],varepsilon]{dot {mathbf {q} ¿Qué?

que puede considerarse como una función de ε. Calculando la derivada en ε' = 0 y usando la regla de Leibniz, obtenemos

0=dI.dε ε [0]=L[q[t2],qÍ Í [t2],t2]T− − L[q[t1],qÍ Í [t1],t1]T+∫ ∫ t1t2∂ ∂ L∂ ∂ q()− − ∂ ∂ φ φ ∂ ∂ qqÍ Í T+∂ ∂ φ φ ∂ ∂ ε ε )+∂ ∂ L∂ ∂ qÍ Í ()− − ∂ ∂ 2φ φ ()∂ ∂ q)2qÍ Í 2T+∂ ∂ 2φ φ ∂ ∂ ε ε ∂ ∂ qqÍ Í − − ∂ ∂ φ φ ∂ ∂ qq.. T)dt.{displaystyle {begin{aligned}0={frac {dI}{dvarepsilon [0]={} {mathbf {q} [t_{2}],{dot {mathbf {q} [t_{2}],t_{2}T-L [mathbf {q} [t_{1}],{dot {mathbf {q} [t_{1}],t_{1}T[6pt] ¿Qué? {partial L}{partial mathbf {q}}left(-{frac {partial varphi }{partial mathbf {q}} { dot {mathbf {q}} {cH} {cH} {cH}}}} {cH0} {cH00}}}} {cH} {cH}}}}}}}}}} {ccH}}}}}}}} {cccccccccH}ccH}cccccccccccHFF} {cHFF} {cHFF}} {cccccccccccHFF}}cH}}}}ccccccccHFF}}}ccc {f} {f}} {f}}f} {f} {f}}f}}}}}} {f} {f} {f}} {f}}f} {f} {f}}f}}}} {f} {f} {f}f}}f}f} {f}f}}}}}f}}}}}f}f}}f}f}f}f}f}f}f}f}}f}f}f}f}f}f}f}f}}f}f}f}f}f} {f}f} {f}}f} {f}f}}f}f}f}f} {f}f}f}f}f}f}}f}f}f}f}}f}f} }{2}T+{frac {partial ^{2}varphi }{partial varepsilon partial mathbf {q} { dot {mathbf {q} {fnMicroc {cHFF}{partial mathbf {q}{ddot {mathbf {}}Tright),dt.end{aligned}}}

Observe que las ecuaciones de Euler-Lagrange implican

ddt()∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ qqÍ Í T)=()ddt∂ ∂ L∂ ∂ qÍ Í )∂ ∂ φ φ ∂ ∂ qqÍ Í T+∂ ∂ L∂ ∂ qÍ Í ()ddt∂ ∂ φ φ ∂ ∂ q)qÍ Í T+∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ qq.. T=∂ ∂ L∂ ∂ q∂ ∂ φ φ ∂ ∂ qqÍ Í T+∂ ∂ L∂ ∂ qÍ Í ()∂ ∂ 2φ φ ()∂ ∂ q)2qÍ Í )qÍ Í T+∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ qq.. T.{fnMicrosoft} {fnK} {fnMicroc {fnMicroc {f} {fnMicroc {f} {fn} {fnMicrosoft}} {fnMicrosoft} {f}}} {fnMicrosoft} {f}}}fnMicroc} {f}}}}}} {f} {f}}}}f}}}}f}f}f}f}f}f}f}}f}f}f}f}f}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}f}f}f}f}f}f}}f}}}}}}}}}} {fnK} {fnMitbf {}} {fnMitbf {f}} {f}} {f}} {fnMitbf {f}} {fnMicrosoft} {fnMicroc {fnMicroc {partial L}{dot {mthbf {}}}}}}derecho) {frac {partial varphi }{mathbf {}}}}}} { dot {mthbf} {f} {f}}}}} {f}}}}}} {f}f} {f}}f}}}}f} {f} {f}f}f}}}f}f}f}}f}f}f}f}f}f}f}f}f}f}f}}f}f}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}f}f} {fnK}}}fnuncio {fnh}}}}m} {fnuncio {f}}m} {fn} {fn} {fnfn} {fnMicroc {cH} {m} {fnMitbf} {fnMitbf}} {f}}}}}}}}}}}}}}}f} {f} {f}}}}f}}}}}} {f} {f} {f}}f}}}}}}}}}}}}}}}}}}}}}}}}f}f}f}} {f} {f} {f}}}}}}}}}}}} {f} {f}f} {f}f}}}}}}}}}}}}}}}}}f}}f}}}}}}}}}}} #T+{frac {partial L}{partial {dot {mathbf {q} {f} {f} {f} {f}} {f}}} {f} {f}} {f}} {f} {f}}} {f}}} {f}}} {f}} {f}} {f}} {f}} {f} {f}f}}}} {f}}} {f} {f}}}}f}}}}}}}}}} {f} {f} {f}}f}}}}}}}}}}}} {f} {f} {f}}}}}}}}}}}}}}}}}}}} {f} {f}} {f}}} {f} {f} {f} {f} {f}}}}f} {f}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}} {fnK} {fnMitb} {fnMitbf {}}}}}left({frac {partial ^{2}varphi }{} {epartial mathbf {q}}}{2}}}}} {dot { dot} { dot} {} {} {f} {f}}} {f}}}} {f}}}}} {f} {f}} {f} {f} {f} {f}} {f} {f} {f}}}}f}f}}}}f}}f}}}}}}}} {f} {f} {f}} {f}}}}}}}}f} {f}f} {f} {f}}}}}f} {f}}}}f}}}}f} {f}}f}}} #T+{frac {partial L}{partial {dot {mathbf {q} {fnK}} {fnMitbf {}} {fnMitbf {f}} {f}} {f}} {fnMitbf {f}}}}} {fnMitbf {f}} T.

Sustituyendo esto en la ecuación anterior, se obtiene

0=dI.dε ε [0]=L[q[t2],qÍ Í [t2],t2]T− − L[q[t1],qÍ Í [t1],t1]T− − ∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ qqÍ Í [t2]T+∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ qqÍ Í [t1]T+∫ ∫ t1t2∂ ∂ L∂ ∂ q∂ ∂ φ φ ∂ ∂ ε ε +∂ ∂ L∂ ∂ qÍ Í ∂ ∂ 2φ φ ∂ ∂ ε ε ∂ ∂ qqÍ Í dt.{displaystyle {begin{aligned}0={frac {dI}{dvarepsilon [0]={} {mathbf {q} [t_{2}],{dot {mathbf {q} [t_{2}],t_{2}]T-L [mathbf {q} [t_{1}],{dot {mathbf {q} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMitbf {f} {fnK} {fnMitbf {}} {fnMitbf {f}} {f}} {f}} {fnMitbf {f}} [t_{2}T+{partial L}{partial {dot {mathbf {q} {fnK} {fnMitbf {}} {fnMitbf {f}} {f}} {f}} {fnMitbf {f}} [t_{1}]T[6pt] ¿Qué? {partial L}{partial mathbf {q}}{frac {partial varphi }{partial varepsilon {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f} {f}fnMicrosoft} }} {frac {partial ^{2}varphi }{partial varepsilon partial mathbf {q}} {dot {mathbf {q}}} {cH} {cH}} {cH}}}} {c}}} {cH0}}}}}}}} {c}}}}}}}}}}}} {c}}}}}} {c}}}}} {c}}}} {c}}}}}}} {c}}}}}}}}}} {cc}}}}}}}}}}}}}} {cccccccccccc}}} {cccc}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {cc },dt.

Usando de nuevo las ecuaciones de Euler-Lagrange obtenemos

ddt()∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ ε ε )=()ddt∂ ∂ L∂ ∂ qÍ Í )∂ ∂ φ φ ∂ ∂ ε ε +∂ ∂ L∂ ∂ qÍ Í ∂ ∂ 2φ φ ∂ ∂ ε ε ∂ ∂ qqÍ Í =∂ ∂ L∂ ∂ q∂ ∂ φ φ ∂ ∂ ε ε +∂ ∂ L∂ ∂ qÍ Í ∂ ∂ 2φ φ ∂ ∂ ε ε ∂ ∂ qqÍ Í .{fnMicroc {fnMicroc} {fnK} {fnMicroc {fnMicrosoft} {f} {fnMicrosoft} {f}} {fnMicrosoft} {fnK} {f} {fnMicrosoft} {f}fnK}f}}}f}f}}}}}}}}}}}}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}}b}b}b}}}}}b}b}b}b}b}b}}}b}b}}}b}b}b}b}b}b}b}}}}}}}}b}}b}b}b}b}}}}}b}}}}}}b}} {fnMicrosoft Sans Serif} {varepsilon }right)=left({frac {d}{dt}}{frac {partial L}partial {dot {mathbf {}}}}}}}}right){frac {partial {varephi } {va}}}}}}}}} {f}}}}}}}}}}} {f}}}}}}}} {f}}}}} {f}}} {f}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f}}}}}}}} {f}}}} {f}}}}}}}}f} {f}} {f}}}}}}} {f}} {f}}}}}}}}}}}}}}}}}} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f} {f}fnMicrosoft} }} {frac {partial ^{2}varphi }{partial varepsilon partial mathbf {q}} {dot {mathbf {q}}} {cH} {cH}}} {cH}}} {c}}} {cH0}}}}}}}} {c}}}}}}}}}}}} {c}}}}}} {c}}}}} {c}}}} {c}}}}}} {c}}}}}}}}}}} {cc}}}}}}}}}}}}}} {cccccccccccccccccc}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}} {c }={frac {partial L}{partial mathbf {q}{frac {partial varphi }{partial varepsilon {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f} {f}fnMicrosoft} }} {frac {partial ^{2}varphi }{partial varepsilon partial mathbf {q}} {dot {mathbf {q}}} {cH} {cH}}} {cH}}} {c}}} {cH0}}}}}}}} {c}}}}}}}}}}}} {c}}}}}} {c}}}}} {c}}}} {c}}}}}} {c}}}}}}}}}}} {cc}}}}}}}}}}}}}} {cccccccccccccccccc}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}} {c }}

Sustituyendo esto en la ecuación anterior, se obtiene

0=L[q[t2],qÍ Í [t2],t2]T− − L[q[t1],qÍ Í [t1],t1]T− − ∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ qqÍ Í [t2]T+∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ qqÍ Í [t1]T+∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ ε ε [t2]− − ∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ ε ε [t1].{displaystyle {begin{aligned}0={} {mathbf {q} [t_{2}],{dot {mathbf {q} [t_{2}],t_{2}T-L [mathbf {q} [t_{1}],{dot {mathbf {q} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMitbf {f} {fnK} {fnMitbf {}} {fnMitbf {f}} {f}} {f}} {fnMitbf {f}} [t_{2}T+{partial L}{partial {dot {mathbf {q} {fnK} {fnMitbf {}} {fnMitbf {f}} {f}} {f}} {fnMitbf {f}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMitbf {cH} {fnK}} {fnMicroc {cH} {cHFF} {cHFF} {f} {fn}} {fn}} {fn} {fn}} {fn}}} {fn}} {fnf}}}}} {fnfnf}}}}} {fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn\fnfnfnfn\\fn\fn\\fnfnfnfnMicroc}}}\\\\\\\\\\\fn}\\\\\\\fnfnK}\fnMicroc {cc # {frac {partial varphi}{partial varepsilon {fnMicrosoft Sans Serif}

De donde se puede ver que

()∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ qqÍ Í − − L)T− − ∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ ε ε {displaystyle left({frac {partial L}{partial {dot {mathbf {q} {fnK} {fnMitbf {}} {fnMitbf {f}} {f}} {f}} {fnMitbf {f}} {fnMicrosoft Sans Serif} # {frac {partial varphi}{partial varepsilon }

es una constante del movimiento, es decir, es una cantidad conservada. Desde φ[q, 0] = q, tenemos ∂ ∂ φ φ ∂ ∂ q=1{displaystyle {frac {partial varphi }{partial mathbf {q} }=1} y así la cantidad conservada simplifica

()∂ ∂ L∂ ∂ qÍ Í qÍ Í − − L)T− − ∂ ∂ L∂ ∂ qÍ Í ∂ ∂ φ φ ∂ ∂ ε ε .{displaystyle left {fnMicroc {fnK} {fnh}}} {fn}} {fn}} {fn}}} {fnMithbf {cH0}}}}}}}} { {fnMicrosoft Sans Serif} # {frac {partial varphi}{partial varepsilon }}

Para evitar una complicación excesiva de las fórmulas, esta derivación supuso que el flujo no cambia con el paso del tiempo. El mismo resultado se puede obtener en el caso más general.

Derivación teórica de campo

El teorema de Noether también puede ser derivado para campos de tensor φ φ A{displaystyle varphi ^{A} donde el índice A abarca los diversos componentes de los diversos campos de tensor. Estas cantidades de campo son funciones definidas en un espacio de cuatro dimensiones cuyos puntos son etiquetados por coordenadas x^μ donde el índice μ rangos con el tiempo (μ= 0) y tres dimensiones espaciales (μ= 1, 2, 3). Estas cuatro coordenadas son las variables independientes; y los valores de los campos en cada evento son las variables dependientes. Bajo una transformación infinitesimal, la variación en las coordenadas está escrita

xμ μ → → .. μ μ =xμ μ +δ δ xμ μ {displaystyle x^{mu}rightarrow xi }=x^{mu }+ delta x^{mu }

mientras que la transformación de las variables de campo se expresa como

φ φ A→ → α α A().. μ μ )=φ φ A()xμ μ )+δ δ φ φ A()xμ μ ).{displaystyle varphi ^{A}rightarrow alpha ^{A}left(xi ^{mu }right)=varphi ^{A}left(x^{mu }right)+delta varphi ^{A}left(x^{mu }right),}

Por esta definición, las variaciones de campo δ δ φ φ A{displaystyle delta varphi ^{A} resultado de dos factores: cambios intrínsecos en el campo ellos mismos y cambios en las coordenadas, desde el campo transformado α^A depende de las coordenadas transformadas Š^μ. Para aislar los cambios intrínsecos, la variación de campo en un solo punto x^μ puede definirse

α α A()xμ μ )=φ φ A()xμ μ )+δ δ ̄ ̄ φ φ A()xμ μ ).{displaystyle alpha ^{A}left(x^{mu }right)=varphi ^{A}left(x^{mu }right)+{bar {delta }varphi ^{A}left(x^{mu }right),}

Si se cambian las coordenadas, el límite de la región del espacio-tiempo sobre el cual se integra el Lagrangiano también cambia; el límite original y su versión transformada se denotan como Ω y Ω’, respectivamente.

El teorema de Noether comienza con la suposición de que una transformación específica de las coordenadas y variables de campo no cambia la acción, que se define como la integral de la densidad lagrangiana sobre la región dada del espacio-tiempo. Expresado matemáticamente, esta suposición se puede escribir como

∫ ∫ Ω Ω .. L()α α A,α α A,.. ,.. μ μ )d4.. − − ∫ ∫ Ω Ω L()φ φ A,φ φ A,.. ,xμ μ )d4x=0{displaystyle int _{ Omega - ¿Qué? - ¿Qué?

donde el subíndice de la coma indica una derivada parcial con respecto a las coordenadas que siguen a la coma, p.

φ φ A,σ σ =∂ ∂ φ φ A∂ ∂ xσ σ .{displaystyle {varphi ^{A}_{,sigma }={frac {partial varphi ^{A}{partial x^{sigma },}

Dado que ξ es una variable ficticia de integración, y dado que el cambio en el límite Ω es infinitesimal por suposición, las dos integrales se pueden combinar usando la versión de cuatro dimensiones del teorema de la divergencia en la siguiente forma

∫ ∫ Ω Ω {}[L()α α A,α α A,.. ,xμ μ )− − L()φ φ A,φ φ A,.. ,xμ μ )]+∂ ∂ ∂ ∂ xσ σ [L()φ φ A,φ φ A,.. ,xμ μ )δ δ xσ σ ]}d4x=0.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}. ¿Qué? Bien.

La diferencia en lagrangianos se puede escribir en primer orden en las variaciones infinitesimales como

[L()α α A,α α A,.. ,xμ μ )− − L()φ φ A,φ φ A,.. ,xμ μ )]=∂ ∂ L∂ ∂ φ φ Aδ δ ̄ ̄ φ φ A+∂ ∂ L∂ ∂ φ φ A,σ σ δ δ ̄ ̄ φ φ A,σ σ .{fnMicrosoft Sans Serif} } {bar {delta {fnMicrosoft Sans Serif}

Sin embargo, debido a que las variaciones se definen en el mismo punto descrito anteriormente, la variación y la derivada se pueden realizar en orden inverso; ellos viajan

δ δ ̄ ̄ φ φ A,σ σ =δ δ ̄ ̄ ∂ ∂ φ φ A∂ ∂ xσ σ =∂ ∂ ∂ ∂ xσ σ ()δ δ ̄ ̄ φ φ A).{displaystyle {bar {delta }{varphi ^{A}_{,sigma }={bar {delta # {frac {partial varphi }{partial x^{sigma {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}} {fnMicrosoft Sans Serif}}}}}} {fnMicroc {fnMicros {fnMicroc {fnMicroc {fnMicrosoft}} {f}}}}}}}}}}}}}}}\\\\\\\\\fnMicrocfnMicrocs}}}}}}}}}}}}}}}}}}}\\\\\\\\\\s\\\\\\\\\\\\\\\\\\\\\\\\\\\s\\\\\\\\ }left({bar {delta}varphi ^{A}right),}

Uso de las ecuaciones de campo de Euler-Lagrange

∂ ∂ ∂ ∂ xσ σ ()∂ ∂ L∂ ∂ φ φ A,σ σ )=∂ ∂ L∂ ∂ φ φ A{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} ##{partial x^{sigma }}left {frac {partial {varphi ^{}_{,sigma }}}}right)={frac {partial L}{partial varphi ^{}}}}}}}}}}}}} {fnuncial {f}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}mm}m}}}}}m}}}}}}}}}}}m}}}}}}m}}}}}}}}} {m} {m} {m}}}m}}}}}}}}}}}}}}}}}}}}}}}m}}}}}}}}}}}m}}}}}}}}}}}m}}

la diferencia en lagrangianos se puede escribir claramente como

[L()α α A,α α A,.. ,xμ μ )− − L()φ φ A,φ φ A,.. ,xμ μ )]=∂ ∂ ∂ ∂ xσ σ ()∂ ∂ L∂ ∂ φ φ A,σ σ )δ δ ̄ ̄ φ φ A+∂ ∂ L∂ ∂ φ φ A,σ σ δ δ ̄ ̄ φ φ A,σ σ =∂ ∂ ∂ ∂ xσ σ ()∂ ∂ L∂ ∂ φ φ A,σ σ δ δ ̄ ̄ φ φ A).{displaystyle {begin{aligned} limite[Lleft(alpha ^{A},{alpha ¿Por qué? {fnMicroc {fnMicroc}{partial {varphi }_{,sigma - Sí. }varphi ^{A}+{partial L}{partial {varphi ^{A}_{,sigma } {bar {delta }{varphi ^{A}_{,sigma }={frac {partial ##{partial x^{sigma {fnMicroc {fnMicroc}{partial {varphi }_{,sigma } {bar {delta }varphi ^{A}derecho).

Por lo tanto, el cambio en la acción se puede escribir como

∫ ∫ Ω Ω ∂ ∂ ∂ ∂ xσ σ {}∂ ∂ L∂ ∂ φ φ A,σ σ δ δ ̄ ̄ φ φ A+L()φ φ A,φ φ A,.. ,xμ μ )δ δ xσ σ }d4x=0.{displaystyle int _{ Omega ##{partial x^{sigma - ¿Qué? {varphi ^{A}_{,sigma } {bar {delta }varphi ^{A}+Lleft(varphi ^{A},{varphi ^{A}_{,nu },x^{mu }right)delta x^{sigma} Bien.

Dado que esto es válido para cualquier región Ω, el integrando debe ser cero

∂ ∂ ∂ ∂ xσ σ {}∂ ∂ L∂ ∂ φ φ A,σ σ δ δ ̄ ̄ φ φ A+L()φ φ A,φ φ A,.. ,xμ μ )δ δ xσ σ }=0.{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} ##{partial x^{sigma - ¿Qué? {varphi ^{A}_{,sigma } {bar {delta }varphi ^{A}+Lleft(varphi ^{A},{varphi ^{A}_{,nu },x^{mu }right)delta x^{sigma} } 'derecha '=0 ',

Para cualquier combinación de las diversas transformaciones de simetría, la perturbación se puede escribir

δ δ xμ μ =ε ε Xμ μ δ δ φ φ A=ε ε Ψ Ψ A=δ δ ̄ ̄ φ φ A+ε ε LXφ φ A{displaystyle {begin{aligned}delta x^{mu } X^{mu }\delta varphi ↑ Psi ^{A}={bar {delta }varphi ^{A}+varepsilon {fnMitcal {fnK}varphi }end{aligned}}

Donde LXφ φ A{displaystyle {mathcal {}_{X}varphi ^{A} es el derivado de Lie de φ φ A{displaystyle varphi ^{A} en el X^μ dirección. Cuando φ φ A{displaystyle varphi ^{A} es un cuero cabelludo o Xμ μ ,.. =0{displaystyle {X^{mu}_{,nu}=0},

LXφ φ A=∂ ∂ φ φ A∂ ∂ xμ μ Xμ μ .{displaystyle {mathcal {}_{X}varphi ^{A}={frac {partial varphi ^{A}}{partial x^{mu} {m} {m}}} {m} {m} {m}}}}}mmm}mmm}mmm}}mm}}mmmmmm}mmmmm}}}mmcm}mmccccccccccccccccccccccccccccccccccccccccccccccccccccccc - Sí.

Estas ecuaciones implican que la variación de campo tomada en un punto es igual

δ δ ̄ ̄ φ φ A=ε ε Ψ Ψ A− − ε ε LXφ φ A.{displaystyle {bar {delta }varphi ^{A}=varepsilon Psi ^{A}-varepsilon {mathcal {L}_{X}varphi ^{A},}

Al diferenciar la divergencia anterior con respecto a ε en ε = 0 y cambiar el signo se obtiene la ley de conservación

∂ ∂ ∂ ∂ xσ σ jσ σ =0{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} ##{partial x^{sigma - Sí. }=0}

donde la corriente conservada es igual

jσ σ =[∂ ∂ L∂ ∂ φ φ A,σ σ LXφ φ A− − LXσ σ ]− − ()∂ ∂ L∂ ∂ φ φ A,σ σ )Ψ Ψ A.{displaystyle j^{sigma }=left[{frac {partial L}{sigma }=left[{frac {partial L}{partial l}{ {varphi ^{A}_{,sigma ♪♪♪♪ [L}_{X}varphi ^{A}-L,X^{sigma }right]-left({frac {partial L}{partial {varphi ^{A}_{,sigma }right)right) Psi ^{A},.}

Derivación de colectores/haces de fibras

Supongamos que tenemos un n- multiplicidad dimensional Riemanniana, M y un múltiple objetivo T. Vamos C{displaystyle {fnMithcal}} ser el espacio de configuración de funciones lisas desde M a T. (Más generalmente, podemos tener secciones lisas de un paquete de fibra sobre M.)

Los ejemplos de esta M en física incluyen:

• En la mecánica clásica, en la formulación Hamiltoniana, M es el manifold unidimensional R{displaystyle mathbb {R}, representando el tiempo y el espacio objetivo es el conjunto de espacios de posiciones generalizadas.
• En teoría de campo, M es el múltiple espacio y el espacio objetivo es el conjunto de valores que los campos pueden tomar en cualquier punto dado. Por ejemplo, si hay m campos de escalar de valor real, φ φ 1,...... ,φ φ m{displaystyle varphi _{1},ldotsvarphi ¿Qué?, entonces el doble objetivo es Rm{displaystyle mathbb {R} {} {m}. Si el campo es un campo vectorial real, entonces el múltiple objetivo es isomorfo a R3{displaystyle mathbb {R} {} {}}}.

Ahora supongamos que hay un funcional

S:C→ → R,{displaystyle {máthcal {fnMithcal} {C}derecha mathbb {R}

llamó a la acción. (Toma valores en R{displaystyle mathbb {R}, en lugar de C{displaystyle mathbb {C}; esto es por razones físicas, y no es importante para esta prueba.)

Para llegar a la versión habitual del teorema de Noether, necesitamos restricciones adicionales sobre la acción. Asumimos S[φ φ ]{fnMicrosoft Sans Serif} es la integral M de una función

L()φ φ ,∂ ∂ μ μ φ φ ,x){displaystyle {mathcal {L}(varphipartial _{mu }varphix)}

llamada la densidad lagrangiana, dependiendo de φ φ {displaystyle varphi }, su derivado y la posición. En otras palabras, para φ φ {displaystyle varphi } dentro C{displaystyle {fnMithcal}}

S[φ φ ]=∫ ∫ ML[φ φ ()x),∂ ∂ μ μ φ φ ()x),x]dnx.{fnMicrosoft Sans Serif} _{M}{mathcal {L}[varphi (x),partial _{mu }varphi (x),x],d^{n}x.}

Supongamos que se nos dan condiciones de límites, es decir, una especificación del valor φ φ {displaystyle varphi } en el límite si M es compacto, o algún límite en φ φ {displaystyle varphi } como x se acerca a ∞. Entonces el subespacio C{displaystyle {fnMithcal}} que consiste en funciones φ φ {displaystyle varphi } tal que todos los derivados funcionales de S{displaystyle {fnMithcal}} a φ φ {displaystyle varphi } son cero, es decir:

δ δ S[φ φ ]δ δ φ φ ()x).. 0{displaystyle {frac {delta {fnMitcal {fnMicrosoft Sans Serif}}approx 0}

y eso φ φ {displaystyle varphi } satisface las condiciones de límites dadas, es el subespacio de las soluciones de shell. (Véase principio de acción estacionaria)

Supongo que tenemos una transformación infinitesimal en C{displaystyle {fnMithcal}}, generado por una derivación funcional, Q tales que

Q[∫ ∫ NLdnx].. ∫ ∫ ∂ ∂ Nfμ μ [φ φ ()x),∂ ∂ φ φ ,∂ ∂ ∂ ∂ φ φ ,...... ]dsμ μ {displaystyle Qleft[int] {L},mathrm {d} ^{n}xright]approx int _{partial N}f^{mu }[varphi (x),partial varphipartial varphildots ],ds_{mu }

para todas las subvariedades compactas N o en otras palabras,

Q[L()x)].. ∂ ∂ μ μ fμ μ ()x){displaystyle Q[{mathcal {L}(x)]approx partial _{mu }f^{mu }(x)}

para todas las x, donde establecemos

L()x)=L[φ φ ()x),∂ ∂ μ μ φ φ ()x),x].{displaystyle {mathcal {}(x)={mathcal {L}[varphi (x),partial _{mu }varphi (x),x].}

Si esto se mantiene dentro y fuera del caparazón, decimos que Q genera una simetría fuera del caparazón. Si esto solo se cumple en el caparazón, decimos que Q genera una simetría en el caparazón. Entonces, decimos que Q es un generador de un grupo de Lie de simetría de un parámetro.

Ahora, para cualquier N, debido al teorema de Euler-Lagrange, en capa (y solo en capa), tenemos

Q[∫ ∫ NLdnx]=∫ ∫ N[∂ ∂ L∂ ∂ φ φ − − ∂ ∂ μ μ ∂ ∂ L∂ ∂ ()∂ ∂ μ μ φ φ )]Q[φ φ ]dnx+∫ ∫ ∂ ∂ N∂ ∂ L∂ ∂ ()∂ ∂ μ μ φ φ )Q[φ φ ]dsμ μ .. ∫ ∫ ∂ ∂ Nfμ μ dsμ μ .{displaystyle {begin{aligned}Qleft[int] ¿Por qué? {fn}fn}m}m}m}m}m}m}m}m}m}m}mmmmmmcH0}m}m}mm}mmmmmmmmcH0cH00cH00cH00cH00cH00cH00cH00cH00cH00cHFFFFFFFFFFFFFFFFFF}cH00cH00}cH00\cH00cH00}cH00}cH00cH00}\\cH00}\\\\\\\\cH00cH00cH00cH00cH00}cH00}cH00}cH00cH00cH00cH00cH00}cH00}\ {L}}{partial varphi }-partial _{mu {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} No.

Dado que esto es cierto para cualquier N, tenemos

∂ ∂ μ μ [∂ ∂ L∂ ∂ ()∂ ∂ μ μ φ φ )Q[φ φ ]− − fμ μ ].. 0.{displaystyle partial _{mu }left[{frac {partial {mathcal {L}} {partial (partial _{mu }varphi)}Q[varphi ]-f^{mu }right]approx 0.}

Pero esta es la ecuación de continuidad para la corriente Jμ μ {displaystyle J. definida por:

Jμ μ =∂ ∂ L∂ ∂ ()∂ ∂ μ μ φ φ )Q[φ φ ]− − fμ μ ,{displaystyle J^{mu ##,=,{fracpartial {mathcal {L}} {partial (partial _{mu }varphi)}Q[varphi ]-f^{mu }}}

que se llama la corriente de Noether asociada con la simetría. La ecuación de continuidad nos dice que si integramos esta corriente en una rebanada similar al espacio, obtenemos una cantidad conservada llamada carga de Noether (siempre y cuando, por supuesto, si M no es compacto, las corrientes se reducen lo suficiente rápido en el infinito).

Comentarios

El teorema de Noether es un teorema del caparazón: se basa en el uso de las ecuaciones de movimiento: la trayectoria clásica. Refleja la relación entre las condiciones de contorno y el principio variacional. Suponiendo que no hay términos de frontera en la acción, el teorema de Noether implica que

∫ ∫ ∂ ∂ NJμ μ dsμ μ .. 0.{displaystyle int _{partial No. }ds_{mu }approx 0.}

Los análogos cuánticos del teorema de Noether implican valores de expectativa (por ejemplo, .∫ ∫ d4x∂ ∂ ⋅ ⋅ J.=0{textstyle leftlangle int d^{4}x~partial cdot {textbf {J}rightrangle =0}) Probing off shell cantidades también son las identidades Ward-Takahashi.

Generalización a álgebras de Lie

Supongamos que tenemos dos derivaciones de simetría Q₁ y Q₂. Entonces, [Q₁, Q₂] también es una derivación de simetría. Veamos esto explícitamente. Déjanos decir

Q1[L].. ∂ ∂ μ μ f1μ μ {displaystyle Q_{1}[{mathcal {L}]approx partial _{mu} }

Q2[L].. ∂ ∂ μ μ f2μ μ {displaystyle Q_{2}[{mathcal {L}]approx partial _{mu} }f_{2} {mu}}

Entonces,

[Q1,Q2][L]=Q1[Q2[L]]− − Q2[Q1[L]].. ∂ ∂ μ μ f12μ μ {displaystyle [Q_{1},Q_{2}] [{mathcal {L}]=Q_{1}[Q_{2} [{mathcal {L}]] [Q_{2} [Q_{1} [mathcal {L}]]approx partial _{mui} }f_{12} {mu}

j12μ μ =()∂ ∂ ∂ ∂ ()∂ ∂ μ μ φ φ )L)()Q1[Q2[φ φ ]]− − Q2[Q1[φ φ ]])− − f12μ μ .{displaystyle {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {f} {cH00}}}} {cH00}}}}} {ccH0}}}}cccccH00}cccH00}cH00}cH00}ccccccH00}ccH00}ccH00}ccccH00}cH00}cH00}cccH00}cH00cH00}cH00}cH00}cH00}cH00}cH00}ccH00}ccH00}}cH00}

Esto demuestra que podemos extender el teorema de Noether a álgebras de Lie más grandes de forma natural.

Generalización de la prueba

Esto se aplica a cualquier derivación de simetría local Q que satisfaga QS ≈ 0, y también a acciones diferenciables funcionales locales más generales, incluidas aquellas en las que el lagrangiano depende de las derivadas superiores de los campos. Sea ε cualquier función uniforme arbitraria de la variedad de espacio-tiempo (o tiempo) tal que el cierre de su soporte sea disjunto de la frontera. ε es una función de prueba. Entonces, debido al principio variacional (que, dicho sea de paso, no se aplica a la frontera), la distribución de derivación q generada por q[ε][Φ(x)] = ε(x)Q[Φ(x)] satisface q[ε][S] ≈ 0 para cada ε, o de forma más compacta, q(x)[S] ≈ 0 para todos los x que no están en el límite (pero recuerda que q(x) es una forma abreviada de una distribución de derivación, no una derivación parametrizada por x en general). Esta es la generalización del teorema de Noether.

Para ver cómo la generalización está relacionada con la versión anterior, asuma que la acción es la parte espacial de un lagrangiano que sólo depende de φ φ {displaystyle varphi } y sus primeros derivados. Además, asuma

Q[L].. ∂ ∂ μ μ fμ μ {displaystyle Q[{mathcal {L}]approx partial _{mu }f^{mu }}

Entonces,

q[ε ε ][S]=∫ ∫ q[ε ε ][L]dnx=∫ ∫ {}()∂ ∂ ∂ ∂ φ φ L)ε ε Q[φ φ ]+[∂ ∂ ∂ ∂ ()∂ ∂ μ μ φ φ )L]∂ ∂ μ μ ()ε ε Q[φ φ ])}dnx=∫ ∫ {}ε ε Q[L]+∂ ∂ μ μ ε ε [∂ ∂ ∂ ∂ ()∂ ∂ μ μ φ φ )L]Q[φ φ ]}dnx.. ∫ ∫ ε ε ∂ ∂ μ μ {}fμ μ − − [∂ ∂ ∂ ∂ ()∂ ∂ μ μ φ φ )L]Q[φ φ ]}dnx{displaystyle {begin{aligned}q[varepsilon][{mathcal {S}] limit=int q[varepsilon ] [{mathcal {L}]d^{n}x[6pt] Varepsilon Q[varphi]+left[{frac] {partial }{partial _{mu }varphi)}{mathcal {L}right]partial _{mu }(varepsilon Q[varphi])right}d^{n}x[6pt] Q[{mathcal {L}]+partial _{mu }varepsilon left[{frac {partial }{partial left(partial _{mu }varphi right)}{mathcal {L}right]Q[varphi ]derecho]. }-left[{frac {partial }{partial (partial _{mu }varphi)}{mathcal {L}right]Q[varphi ]right},d^{n}xend{aligned}}} {fn}} {fn}}} {fnfnfnfn}} {fn}}}}}} {f}}}}}}}}}}}}}}}}}}} {f}}}}} {f} {f}}}}}}}}}} {

para todos ε ε {displaystyle varepsilon }.

De forma más general, si el lagrangiano depende de derivadas superiores, entonces

∂ ∂ μ μ [fμ μ − − [∂ ∂ ∂ ∂ ()∂ ∂ μ μ φ φ )L]Q[φ φ ]− − 2[∂ ∂ ∂ ∂ ()∂ ∂ μ μ ∂ ∂ .. φ φ )L]∂ ∂ .. Q[φ φ ]+∂ ∂ .. [[∂ ∂ ∂ ∂ ()∂ ∂ μ μ ∂ ∂ .. φ φ )L]Q[φ φ ]]− − ⋯ ⋯ ].. 0.{displaystyle partial _{mu. }-left[{frac {partial }{partial _{mu }varphi)}{mathcal {L}right]Q[varphi ]-2left[{frac] {partial }{partial {fnMicrosoft Sans Serif} 0.}

Ejemplos

Ejemplo 1: Conservación de la energía

Mirando el caso específico de una partícula newtoniana de masa m, coordenada x, moviéndose bajo la influencia de un potencial V, coordinado por tiempo t. La acción, S, es:

S[x]=∫ ∫ L[x()t),xÍ Í ()t)]dt=∫ ∫ ()m2.. i=13xÍ Í i2− − V()x()t)))dt.{displaystyle {begin{aligned}{mathcal {S} {x}=int Lleft[x(t),{dot {x} {x}(t)right],dt\=int left({frac {m}{2}}sum}sum ¿Qué? {x}_{i} {2}-V(x(t)right),dt.end{aligned}}}

El primer término entre corchetes es la energía cinética de la partícula, mientras que el segundo es su energía potencial. Considere el generador de traducciones de tiempo Q = d/♪. En otras palabras, Q[x()t)]=xÍ Í ()t){displaystyle Q[x(t)]={dot {x}(t)}. La coordenadas x tiene una dependencia explícita del tiempo, mientras V no; en consecuencia:

Q[L]=ddt[m2.. ixÍ Í i2− − V()x)]=m.. ixÍ Í ix.. i− − .. i∂ ∂ V()x)∂ ∂ xixÍ Í i{displaystyle Q[L]={dt}left[{frac] {m}{2}sum _{i}{dot {x}_{i} {2}-V(x)right]=msum _{i}{dot {x}_{i}{ddot {x}_{i}-sum ¿Qué? ################################################################################################################################################################################################################################################################ {x}_{i}

para que podamos establecer

L=m2.. ixÍ Í i2− − V()x).{displaystyle L={frac {m}{2}sum _{i}{dot {x}_{i} {2}-V(x). }

Entonces,

j=.. i=13∂ ∂ L∂ ∂ xÍ Í iQ[xi]− − L=m.. ixÍ Í i2− − [m2.. ixÍ Í i2− − V()x)]=m2.. ixÍ Í i2+V()x).{displaystyle {begin{aligned}j ventaja=sum {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft Sans Serif} ¿Qué? {x}_{i} {2}-left[{frac} {m}{2}sum _{i}{dot {x}_{i} {2}-V(x)right[3pt] {m}{2}sum ¿Qué? {x}_{i} {2}+V(x)end{aligned}}

El lado derecho es la energía, y el teorema de Noether afirma que dj/dt=0{displaystyle dj/dt=0} (es decir, el principio de conservación de la energía es una consecuencia de la invariancia en las traducciones del tiempo).

Más generalmente, si el Lagrangiano no depende explícitamente del tiempo, la cantidad

.. i=13∂ ∂ L∂ ∂ xÍ Í ixiÍ Í − − L{displaystyle sum _{i=1}{3}{frac {partial L}{partial {dot} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}}} {fn}}}} {f}}}} {fn}}}} {fn}}}}}}} {f}}}} {f}}}}} {f}}}}}}}} {f}}}}}}}}} { {x_{i}}-L}

(llamado hamiltoniano) se conserva.

Ejemplo 2: Conservación del centro de impulso

Aún considerando el tiempo unidimensional, sea

<math alttext="{displaystyle {begin{aligned}{mathcal {S}}left[{vec {x}}right]&=int {mathcal {L}}left[{vec {x}}(t),{dot {vec {x}}}(t)right]dt\[3pt]&=int left[sum _{alpha =1}^{N}{frac {m_{alpha }}{2}}left({dot {vec {x}}}_{alpha }right)^{2}-sum _{alpha S[x→ → ]=∫ ∫ L[x→ → ()t),x→ → Í Í ()t)]dt=∫ ∫ [.. α α =1Nmα α 2()x→ → Í Í α α )2− − .. α α .β β Vα α β β ()x→ → β β − − x→ → α α )]dt,{fnMicrosoft Sans {fnMicrosoft Sans} {fnMicrosoft} {fnMicros {f}}} {fnMitcal {fnMicrosoft} {fnMicrosoft ] {fnMicrosoft} {fnMicrosoft ] {fnMicrosoft ] {fnMicrosoft ] {f} {f} {f} {fnMicrox} {f} {fnMicrox} {f} {fnMicrox} {fnMicrox} {f} {fnMicrox}fnMicrosoft} {fnMicrosoft}fnMicrox} {fnMicrox} {fnMicrox} {f}f}fnMicrox} {f} {f} {fnMicrox}fnMicrox} {fnMicrox} {fnMicrox} {f} { =1}{N}{frac {m_{i}alfa }{2}left({dot {vec} {x}}_{alpha }right)}{2}-sum _{alpha = {beta }V_{alpha beta}left({vec {x}_{beta {fnMicrosoft Sans Serif}<img alt="{displaystyle {begin{aligned}{mathcal {S}}left[{vec {x}}right]&=int {mathcal {L}}left[{vec {x}}(t),{dot {vec {x}}}(t)right]dt\[3pt]&=int left[sum _{alpha =1}^{N}{frac {m_{alpha }}{2}}left({dot {vec {x}}}_{alpha }right)^{2}-sum _{alpha

o N{displaystyle N} Las partículas newtonianas donde el potencial sólo depende del desplazamiento relativo.

Para Q→ → {displaystyle {vec}}, considere el generador de transformaciones galileas (es decir, un cambio en el marco de referencia). En otras palabras,

Qi[xα α j()t)]=tδ δ ij.{displaystyle Q_{i}left[x_{alpha } {j}(t)right]=tdelta _{i}{j}.}

Y

<math alttext="{displaystyle {begin{aligned}Q_{i}[{mathcal {L}}]&=sum _{alpha }m_{alpha }{dot {x}}_{alpha }^{i}-sum _{alpha Qi[L]=.. α α mα α xÍ Í α α i− − .. α α .β β t∂ ∂ iVα α β β ()x→ → β β − − x→ → α α )=.. α α mα α xÍ Í α α i.{displaystyle {begin{aligned}Q_{i}[{mathcal {L}] }m_{alpha {fnMicrosoft Sans Serif} ################################################################################################################################################################################################################################################################ ¿Qué? {x}_{beta }-{vec {x} {alpha }right)\fnMicrosoft Sans Serif _{alpha }m_{alpha }{i}.<img alt="{displaystyle {begin{aligned}Q_{i}[{mathcal {L}}]&=sum _{alpha }m_{alpha }{dot {x}}_{alpha }^{i}-sum _{alpha

Esto tiene la forma de ddt.. α α mα α xα α i{textstyle {frac {d} {dt}sum} _{alpha }m_{alpha }x_{alpha } {i} así podemos

f→ → =.. α α mα α x→ → α α .{displaystyle {vec}=sum} _{alpha }m_{alpha }{vec {x}_{alpha }

Entonces,

j→ → =.. α α ()∂ ∂ ∂ ∂ x→ → Í Í α α L)⋅ ⋅ Q→ → [x→ → α α ]− − f→ → =.. α α ()mα α x→ → Í Í α α t− − mα α x→ → α α )=P→ → t− − Mx→ → CM{displaystyle {begin{aligned}{vec} {fnK} {fnMicrosoft } {fnMicrosoft } {fnMicrosoft } {fnMicrosoft } {fnMicrosoft } {fnMicrosoft } {fnMicrosoft } {fnMicrosoft } {fnMicrosoft } {fnMicrosoft }f}f}f}f}f}fnf}fnfnfnMicrocfnMicrocfnfnMicroc}fnMicroc}fnMicroc}fnf}\fn\fnfnfnMicrocfnKf}fnMicroc}fnMicroc\fnfn\\\\fnfnMicrocfnMicrocfn\\\\\fn}fnMicroc {x}_{alpha {fnK}cdot {fnh}cdot {vc}left[{vec {x}_{alpha }right]-{vec {f}[6pt] limit=sum _{alpha }left(m_{alpha }{dot { dot {vec}} {c}} {f} {cdot}}} {cdot {c}}}}} {cdot {c}} {c}} {cdot}} {c}}}}} {c}}}} {c}} {c}}}}} {f} {cdot} {cdot} {cdot {c}} {cdot {\cdot {c}}}}}}}}} {c}}}} {cdot {c}}} {cdot}}} {c {x}_{alpha }t-m_{alpha {fnMicrosoft Sans Serif}[3pt] {P}t-M{vec} {x}_{CM}end{aligned}}

Donde P→ → {displaystyle {vec}} es el impulso total, M es la masa total y x→ → CM{displaystyle {vec {x}_{CM}} es el centro de la masa. El teorema de Noether dice:

dj→ → dt=0⇒ ⇒ P→ → − − Mx→ → Í Í CM=0.{displaystyle {frac {fnMicroc} {}} {} {f}=0}Rightarrow {vec}-M{dot {vec} {x}_{CM}=0}

Ejemplo 3: Transformación conforme

Ambos ejemplos 1 y 2 están sobre una variedad unidimensional (tiempo). Un ejemplo relacionado con el espacio-tiempo es una transformación conforme de un campo escalar real sin masa con un potencial cuártico en el espacio-tiempo (3 + 1)-Minkowski.

S[φ φ ]=∫ ∫ L[φ φ ()x),∂ ∂ μ μ φ φ ()x)]d4x=∫ ∫ ()12∂ ∂ μ μ φ φ ∂ ∂ μ μ φ φ − − λ λ φ φ 4)d4x{fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f} {f}f}f}f}f}f}f}f}fnMicrosoft}f}f}f}f}fnMicrob}fnKfnKfnKf}fnKf}fnKf}fnKfnKf}fnun}fnKf}fnKfnKfnKfnKfnMinKfnKfnKf}fnKf}fnK}f}fnMin

Para Q, considere el generador de un reescalado de espacio-tiempo. En otras palabras,

Q[φ φ ()x)]=xμ μ ∂ ∂ μ μ φ φ ()x)+φ φ ()x).{displaystyle Q[varphi (x)]=x^{mu }partial _{mu }varphi (x)+varphi (x).}

El segundo término en el lado derecho se debe al "peso constructivo" de φ φ {displaystyle varphi }. Y

Q[L]=∂ ∂ μ μ φ φ ()∂ ∂ μ μ φ φ +x.. ∂ ∂ μ μ ∂ ∂ .. φ φ +∂ ∂ μ μ φ φ )− − 4λ λ φ φ 3()xμ μ ∂ ∂ μ μ φ φ +φ φ ).{displaystyle Q[{mathcal {L}]=partial ^{mu }varphi left(partial _{mu }varphi +x^{nu }partial _{mumu }partial _{nu }varphi +partial _{mu }varphi right)-4lambda varphi ^{3}left(x^{mu }partial _{mu }varphi +varphi right). }

Esto tiene la forma de

∂ ∂ μ μ [12xμ μ ∂ ∂ .. φ φ ∂ ∂ .. φ φ − − λ λ xμ μ φ φ 4]=∂ ∂ μ μ ()xμ μ L){displaystyle partial _{mu }left[{frac {1}{2}x^{mu} }partial ^{nu }varphi partial _{nu }varphi - 'lambda x^{mu }varphi ^{4}right]=partial _{mu }left(x^{mu }{mathcal {L}right)}

(donde hemos realizado un cambio de índices ficticios) así que establezca

fμ μ =xμ μ L.{displaystyle f^{mu} }=x^{mu # {fnMitcal {L}}

Entonces

jμ μ =[∂ ∂ ∂ ∂ ()∂ ∂ μ μ φ φ )L]Q[φ φ ]− − fμ μ =∂ ∂ μ μ φ φ ()x.. ∂ ∂ .. φ φ +φ φ )− − xμ μ ()12∂ ∂ .. φ φ ∂ ∂ .. φ φ − − λ λ φ φ 4).{displaystyle {begin{aligned}j^{mu } limit=left[{frac] {partial }{partial _{mu }varphi)}{mathcal {L}right]Q[varphi ]-f^{mu] }varphi left(x^{nu }partial _{nu }varphi +varphi right)-x^{mu }left({frac {1}{2}partial ^{nu }varphi partial _{nu }varphi -lambda varphi ¿Qué?

El teorema de Noether declara que ∂ ∂ μ μ jμ μ =0{displaystyle partial _{mu }j^{mu }=0} (como se puede comprobar explícitamente sustituyendo las ecuaciones Euler-Lagrange en el lado izquierdo).

Si uno trata de encontrar el análogo Ward-Takahashi de esta ecuación, se encuentra con un problema debido a las anomalías.

Aplicaciones

La aplicación del teorema de Noether permite a los físicos obtener conocimientos profundos sobre cualquier teoría general de la física, simplemente analizando las diversas transformaciones que harían invariante la forma de las leyes involucradas. Por ejemplo:

• Invariancia de un sistema aislado con respecto a la traducción espacial (en otras palabras, que las leyes de la física son las mismas en todos los lugares del espacio) da la ley de conservación del impulso lineal (que establece que el impulso lineal total de un sistema aislado es constante)
• La invariancia de un sistema aislado con respecto a la traducción del tiempo (es decir, que las leyes de la física son las mismas en todos los puntos del tiempo) da la ley de conservación de la energía (que afirma que la energía total de un sistema aislado es constante)
• La invariancia de un sistema aislado con respecto a la rotación (es decir, que las leyes de la física son las mismas con respecto a todas las orientaciones angulares en el espacio) da la ley de conservación del impulso angular (que establece que el impulso angular total de un sistema aislado es constante)
• La invariancia de un sistema aislado con respecto a los impulsos de Lorentz (es decir, que las leyes de la física son las mismas con respecto a todos los marcos de referencia inerciales) da el teorema central de masa (que indica que el centro de masa de un sistema aislado se mueve a una velocidad constante).

En la teoría cuántica de campos, el análogo al teorema de Noether, la identidad de Ward-Takahashi, genera más leyes de conservación, como la conservación de la carga eléctrica a partir de la invariancia con respecto a un cambio en el factor de fase del campo complejo de la partícula cargada y el indicador asociado del potencial eléctrico y potencial vectorial.

La carga de Noether también se usa para calcular la entropía de los agujeros negros estacionarios.