Teorema de la bisectriz del ángulo

En geometría, la ángulo bisector teorema se preocupa por las longitudes relativas de los dos segmentos que el lado de un triángulo se divide en una línea que se biseca el ángulo opuesto. equipara sus longitudes relativas a las longitudes relativas de los otros dos lados del triángulo.
Theorem
Considerar un triángulo ABC. Dejar el bisector de ángulo ∠ A intersect side BC en un momento D entre B y C. El teorema bisector del ángulo indica que la relación de la longitud del segmento de línea BD a la longitud del segmento CD es igual a la relación de la longitud del lado AB a la longitud del lado AC:
y a la inversa, si un punto D en el lado BC de △ABC divide BC en la misma proporción que los lados AB y AC, luego AD es la bisectriz del ángulo ∠ A.
El teorema de la bisectriz generalizada establece que si D se encuentra en la recta BC, luego
Esto se reduce a la versión anterior si AD es la bisectriz de ∠ BAC. Cuando D es externo al segmento < span style="text-decoration:overline;">BC, en el cálculo se deben utilizar segmentos de línea dirigidos y ángulos dirigidos.
El teorema de la bisectriz de un ángulo se usa comúnmente cuando se conocen las bisectrices de los ángulos y las longitudes de los lados. Se puede utilizar en un cálculo o en una prueba.
Una consecuencia inmediata del teorema es que la bisectriz del ángulo del vértice de un triángulo isósceles también bisecará el lado opuesto.
Pruebas
Existen muchas formas diferentes de demostrar el teorema de la bisectriz del ángulo. Algunos de ellos se muestran a continuación.
Demostración usando triángulos semejantes
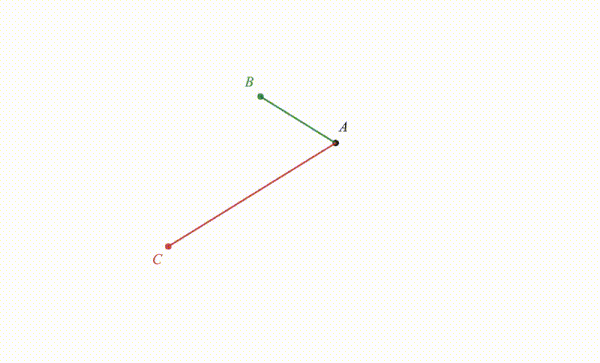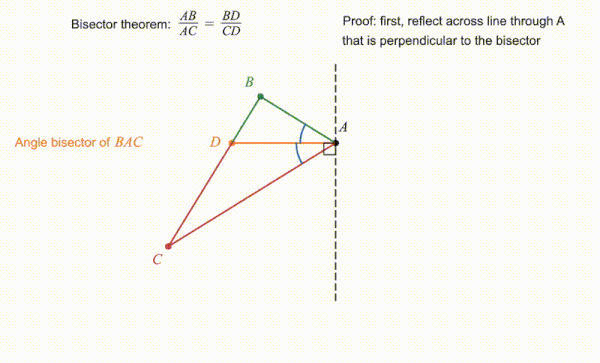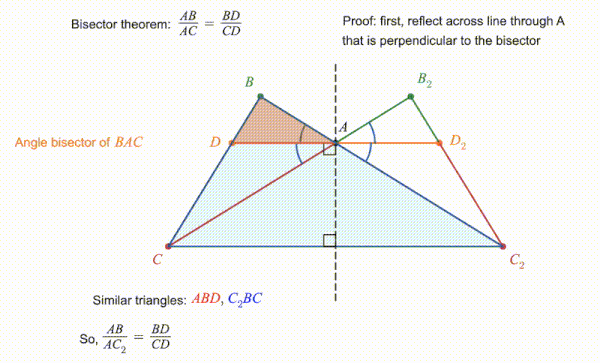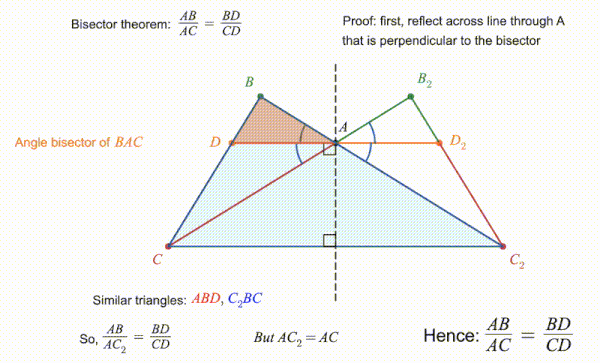
Como se muestra en la animación acompañante, el teorema se puede probar utilizando triángulos similares. En la versión ilustrada aquí, el triángulo se refleja en una línea perpendicular al bisector del ángulo , resultando en el triángulo con bisector . El hecho de que los ángulos producidos por la bisección y son iguales significa que y son líneas rectas. Esto permite la construcción del triángulo que es similar a . Debido a que las relaciones entre los lados correspondientes de triángulos similares son todos iguales, sigue que . Sin embargo, fue construido como un reflejo de la línea , y por lo tanto esas dos líneas son de igual longitud. Por lo tanto, , dando el resultado declarado por el teorema.
Demostración utilizando la ley de los senos
En el diagrama anterior, utilice la ley de los senos en los triángulos △ABD y △ACD :
()1)
()2)
Los ángulos ∠ ADB y ∠ ADC forman una línea par, es decir, son ángulos suplementarios adyacentes. Como los ángulos suplementarios tienen senos iguales,
Angles ∠ DAB y ∠ DAC son iguales. Por lo tanto, los lados de mano derecha de las ecuaciones (1) y (2) son iguales, por lo que sus lados izquierdos también deben ser iguales.
que es el teorema bisector angular.
Si ángulos ∠ DAB, ∠ DAC son desiguales, ecuaciones (1) y (2) puede ser re-escrito como:
Los ángulos ∠ ADB, ∠ ADC siguen siendo suplementarios, por lo que los lados derechos de estas ecuaciones siguen siendo iguales , entonces obtenemos:
que reorganiza a la categoría "generalizada" versión del teorema.
Demostración usando altitudes de triángulos

Sea D un punto en la recta BC, distinto de B o C y tal que AD no es una altitud del triángulo △ABC.
Vamos. B1 ser la base (pie) de la altitud en el triángulo ABD a través de B y dejar C1 ser la base de la altitud en el triángulo ACD a través de C. Entonces, si D es estrictamente entre B y C, uno y sólo uno de B1 o C1 mentiras dentro ABC y puede ser asumido sin pérdida de generalidad que B1 Sí. Este caso se describe en el diagrama adyacente. Si D mentiras fuera del segmento BC, entonces ninguno B1 ni C1 miente dentro del triángulo.
∠ DB1B, ∠ DC1 C son ángulos rectos, mientras que los ángulos ∠ B1DB, ∠ C1DC son congruentes si D se encuentra en el segmento BC (es decir, entre B y C) y son idénticos en los demás casos considerados, por lo que los triángulos △DB1B, △DC1C son similares (AAA), lo que implica que:
Si D es el pie de una altitud, entonces,
y la forma generalizada sigue.
Demostración usando áreas de triángulos

Una prueba rápida se puede obtener mirando la relación de las áreas de los dos triángulos BAD, CAD, que se crean por el bisector de ángulo en A. Computing those areas twice using different formulas, that is con base g y altitud h y con lados a, b y su ángulo cerrado γ, dará el resultado deseado.
Vamos. h denota la altura de los triángulos en la base BC y ser la mitad del ángulo en A. Entonces...
y
rendimiento
Longitud del bisector del ángulo

La longitud del bisector del ángulo puede ser encontrado por ,
Donde es la constante de proporcionalidad del teorema bisector angular.
Demostración: Según el teorema de Stewart, tenemos
Bisectrices de ángulos exteriores
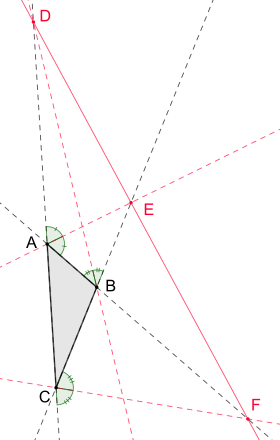
Puntos D, E, F son collinear y las siguientes ecuaciones para la fijación de ratios:
, ,
Para los bisectores de ángulo exterior en un triángulo no equilateral existen ecuaciones similares para las proporciones de las longitudes de los lados del triángulo. Más precisamente si el bisector del ángulo exterior A interseca el lado extendido BC dentro E, el bisector de ángulo exterior en B interseca el lado extendido AC dentro D y el bisector de ángulo exterior en C interseca el lado extendido AB dentro F, entonces las siguientes ecuaciones sostienen:
- , ,
Los tres puntos de intersección entre las bisectrices del ángulo exterior y los lados extendidos del triángulo D, E, F son colineales, es decir ¿Se encuentran en una línea común?
Historia
El teorema de la bisectriz del ángulo aparece como la Proposición 3 del Libro VI de los Elementos de Euclides. Según Heath (1956, p. 197 (vol. 2)), Robert Simson dio la declaración correspondiente para una bisectriz de ángulo externo, quien señaló que Pappus asumió este resultado sin pruebas. Heath continúa diciendo que Augustus De Morgan propuso que las dos declaraciones se combinaran de la siguiente manera:
- Si un ángulo de un triángulo es bisecado interna o externamente por una línea recta que corta el lado opuesto o el lado opuesto producido, los segmentos de ese lado tendrán la misma relación que los otros lados del triángulo; y, si un lado de un triángulo se divide interna o externamente para que sus segmentos tengan la misma relación que los otros lados del triángulo, la línea recta dibujada desde el punto de la sección al punto angular que es opuesto al primer bisecto.
Aplicaciones
Este teorema se ha utilizado para demostrar los siguientes teoremas/resultados:
- Coordenadas del incentro de un triángulo
- Círculos de Apolonio









































