Teorema de König (teoría de grafos)

En el área matemática de la teoría de grafos, el teorema de Kőnig, demostrado por Dénes Kőnig (1931), describe una equivalencia entre el problema de correspondencia máxima y el problema de cobertura mínima de vértices en grafos bipartitos. Fue descubierto de forma independiente, también en 1931, por Jenő Egerváry en el caso más general de grafos ponderados.

Una cobertura de vértices en un grafo es un conjunto de vértices que incluye al menos un punto final de cada arista, y una cobertura de vértices es mínima si ninguna otra cobertura de vértices tiene menos vértices. Una coincidencia en un grafo es un conjunto de aristas de las cuales ninguna de dos comparte un punto final, y una coincidencia es máxima si ninguna otra coincidencia tiene más aristas.

Es obvio a partir de la definición que cualquier conjunto de cobertura de vértices debe ser al menos tan grande como cualquier conjunto coincidente (ya que para cada arista en la coincidencia, se necesita al menos un vértice en la cobertura). En particular, el conjunto de cobertura de vértices mínimo es al menos tan grande como el conjunto coincidente máximo. El teorema de König establece que, en cualquier grafo bipartito, el conjunto de cobertura de vértices mínimo y el conjunto coincidente máximo tienen de hecho el mismo tamaño.

En cualquier gráfico bipartito, el número de bordes en una combinación máxima equivale al número de vértices en una cubierta mínima de vértice.

El grafo bipartito que se muestra en la ilustración anterior tiene 14 vértices; un emparejamiento con seis aristas se muestra en azul y una cobertura de vértices con seis vértices se muestra en rojo. No puede haber una cobertura de vértices menor, porque cualquier cobertura de vértices debe incluir al menos un punto final de cada arista emparejada (así como de cada una de las otras aristas), por lo que se trata de una cobertura de vértices mínima. De manera similar, no puede haber un emparejamiento mayor, porque cualquier arista emparejada debe incluir al menos un punto final en la cobertura de vértices, por lo que se trata de un emparejamiento máximo. El teorema de König establece que la igualdad entre los tamaños del emparejamiento y la cobertura (en este ejemplo, ambos números son seis) se aplica de manera más general a cualquier grafo bipartito.

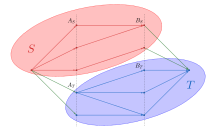
La siguiente prueba proporciona una manera de construir una cubierta mínima de vértice desde un ajuste máximo. Vamos. ${\displaystyle G=(V,E)}$ ser un gráfico bipartito y dejar ${\displaystyle A,B}$ ser las dos partes del conjunto del vértice ${\displaystyle V}$. Supongamos que ${\displaystyle M}$ es una combinación máxima para ${\displaystyle G.$.

Construir la red de flujo ${\displaystyle G'_{\infty}$ derivada ${\displaystyle G.$ de tal manera que hay bordes de capacidad ${\displaystyle 1}$ de la fuente ${\displaystyle s}$ a cada vértice ${\displaystyle a\in A}$ y de cada vértice ${\displaystyle b\in B}$ al sumidero ${\displaystyle t}$, y de capacidad ${\displaystyle +\infty}$ desde ${\displaystyle a}$ a ${\displaystyle b}$ para cualquier ${\displaystyle (a,b)\in E}$.

El tamaño ${\displaystyle TENSIFICADO }$ de la máxima coincidencia en ${\displaystyle G.$ es el tamaño de un flujo máximo en ${\displaystyle G'_{\infty}$, que a su vez es el tamaño de un corte mínimo en la red ${\displaystyle G'_{\infty}$, como sigue del teorema de corte máx.

Vamos. ${\displaystyle (S,T)}$ ser un corte mínimo. Vamos. ${\displaystyle A=A_{S}\cup A_{T}$ y ${\displaystyle B=B_{S}\cup B_{T}$, tal que ${\displaystyle A_{S},B_{S}\subset S.$ y ${\displaystyle A_{T},B_{T}\subset T}$. Luego el corte mínimo se compone sólo de bordes que van desde ${\displaystyle s}$ a ${\displaystyle A_{T}$ o desde ${\displaystyle B_{S}$ a ${\displaystyle t}$, como cualquier borde de ${\displaystyle A_{S}$ a ${\displaystyle B_{T}$ haría el tamaño del corte infinito.

Por lo tanto, el tamaño del corte mínimo es igual a ${\displaystyle SilencioA_{T}$. Por otro lado, ${\displaystyle A_{T}\cup B_{S}$ es una cubierta de vértice, como cualquier borde que no es incidente a vértices de ${\displaystyle A_{T}$ y ${\displaystyle B_{S}$ debe ser un incidente a un par de vértices de ${\displaystyle A_{S}$ y ${\displaystyle B_{T}$, que contradice el hecho de que no hay bordes entre ${\displaystyle A_{S}$ y ${\displaystyle B_{T}$.

Así, ${\displaystyle A_{T}\cup B_{S}$ es una cubierta mínima de vértice ${\displaystyle G.$.

Ningún vértice en una cubierta de vértice puede cubrir más de un borde de ${\displaystyle M}$ (porque el borde de la media vuelta evitaría ${\displaystyle M}$ de ser una coincidencia en el primer lugar), así que si una cubierta de vértice con ${\displaystyle TENSIFICADO }$ vertices se pueden construir, debe ser una cubierta mínima.

Para construir tal cubierta, deja ${\displaystyle U}$ ser el conjunto de vértices inigualables en ${\displaystyle A}$ (posiblemente vacío), y ${\displaystyle Z}$ ser el conjunto de vértices que están ${\displaystyle U}$ o están conectados ${\displaystyle U}$ alternando caminos (patos que se alternan entre bordes que están en los bordes que coinciden y que no están en el emparejado). Vamos.

${\displaystyle K=(A\setminus Z)\cup (B\cap Z).}$

Cada borde ${\displaystyle e}$ dentro ${\displaystyle E}$ pertenece a un camino alternativo (y tiene un punto final derecho en ${\displaystyle K}$), o tiene un punto final izquierdo en ${\displaystyle K}$. Para, si ${\displaystyle e}$ es igualado pero no en un camino alternativo, entonces su punto final izquierdo no puede estar en un camino alternado (porque dos bordes emparejados no pueden compartir un vértice) y por lo tanto pertenece a ${\displaystyle A\setminus Z}$. Alternativamente, si ${\displaystyle e}$ es inigualable pero no en un camino alternado, entonces su punto final izquierdo no puede estar en un camino alternado, porque tal camino podría ser extendido añadiendo ${\displaystyle e}$ a ella. Así, ${\displaystyle K}$ forma una cubierta de vértice.

Además, cada vértice en ${\displaystyle K}$ es un punto final de un borde emparejado. Por, cada vértice en ${\displaystyle A\setminus Z}$ se combina porque ${\displaystyle Z}$ es un superset de ${\displaystyle U}$, el conjunto de vértices izquierdos sin igual. Y cada vértice en ${\displaystyle B\cap Z}$ También debe ser igualado, porque si existiera un camino alternado a un vertex sin igual y luego cambiar el emparejamiento eliminando los bordes emparejados de este camino y añadiendo los bordes inigualables en su lugar aumentaría el tamaño del emparejado. Sin embargo, ningún borde igualado puede tener ambos puntos finales en ${\displaystyle K}$. Así, ${\displaystyle K}$ es una cubierta de vértice de la cardenalidad igual a ${\displaystyle M}$, y debe ser una cubierta mínima de vértice.

Para explicar esta prueba, primero tenemos que extender la noción de un emparejamiento a la de un emparejamiento fraccionario: una asignación de un peso en [0,1] a cada arista, de modo que la suma de pesos cerca de cada vértice sea como máximo 1 (un emparejamiento integral es un caso especial de un emparejamiento fraccionario en el que los pesos están en {0,1}). De manera similar, definimos una cobertura de vértices fraccionaria: una asignación de un peso no negativo a cada vértice, de modo que la suma de pesos en cada arista sea al menos 1 (una cobertura de vértices integral es un caso especial de una cobertura de vértices fraccionaria en la que los pesos están en {0,1}).

El tamaño máximo de emparejamiento fraccional en un gráfico ${\displaystyle G=(V,E)}$ es la solución del siguiente programa lineal:

Maximizar 1_E · x

Sujeto a: x ≥ 0_E

_______ A_G · x ≤ 1_V.

Donde x es un vector de tamaño ¦ESilencio en el que cada elemento representa el peso de un borde en la coincidencia fraccional. 1_E es un vector de la vidaETENCIÓN, por lo que la primera línea indica el tamaño de la coincidencia. 0_E es un vector de la vidaEtención ceros, por lo que la segunda línea indica la limitación de que los pesos no son negativos. 1_V es un vector de la vidaVTENIDOS A_G es la matriz de incidencia G, así que la tercera línea indica la limitación de que la suma de pesos cerca de cada vértice es en la mayoría 1. Del mismo modo, el tamaño mínimo de la cubierta de vértice fraccional en ${\displaystyle G=(V,E)}$ es la solución del siguiente LP:

Minimize 1_V · Sí.

Sujeto a: Sí. ≥ 0_V

_______ A_G^T · Sí. ≥ 1_E.

donde y es un vector de tamaño |V| en el que cada elemento representa el peso de un vértice en la cobertura fraccionaria. Aquí, la primera línea es el tamaño de la cobertura, la segunda línea representa la no negatividad de los pesos y la tercera línea representa el requisito de que la suma de los pesos cerca de cada arista debe ser al menos 1. Ahora, la cobertura fraccionaria mínima LP es exactamente el programa lineal dual del LP de coincidencia fraccionaria máxima. Por lo tanto, por el teorema de dualidad LP, ambos programas tienen la misma solución. Este hecho es cierto no solo en grafos bipartitos sino en grafos arbitrarios:

En cualquier gráfico, el tamaño más grande de una coincidencia fraccional equivale al tamaño más pequeño de una cubierta de vértice fraccional.

Lo que hace que los grafos bipartitos sean especiales es que, en ellos, ambos programas lineales tienen soluciones óptimas en las que todos los valores de las variables son enteros. Esto se desprende del hecho de que en el politopo de correspondencia fraccionaria de un grafo bipartito, todos los puntos extremos tienen solo coordenadas enteras, y lo mismo es cierto para el politopo de cobertura de vértices fraccionario. Por lo tanto, el teorema anterior implica:

En cualquier gráfico bipartito, el tamaño más grande de un emparejado equivale al tamaño más pequeño de una cubierta de vértice.

La prueba constructiva descrita anteriormente proporciona un algoritmo para producir una cobertura mínima de vértices dada una correspondencia máxima. Por lo tanto, el algoritmo de Hopcroft-Karp para encontrar correspondencias máximas en grafos bipartitos también puede utilizarse para resolver el problema de cobertura de vértices de manera eficiente en estos grafos.

A pesar de la equivalencia de los dos problemas desde el punto de vista de las soluciones exactas, no son equivalentes para los algoritmos de aproximación. Los emparejamientos máximos bipartitos se pueden aproximar con una precisión arbitraria en tiempo constante mediante algoritmos distribuidos; en cambio, la aproximación de la cobertura mínima de vértices de un grafo bipartito requiere al menos un tiempo logarítmico.

En el gráfico mostrado en la introducción tomar ${\displaystyle L.$ ser el conjunto de vértices en la capa inferior del diagrama y ${\displaystyle R.$ ser el conjunto de vértices en la capa superior del diagrama. De izquierda a derecha etiquetar los vértices en la capa inferior con los números 1, ..., 7 y etiquetar los vértices en la capa superior con los números 8, ..., 14. ${\displaystyle U}$ de vértices inigualables ${\displaystyle L.$ es {1}. Los caminos alternantes a partir de ${\displaystyle U}$ son 1–10–3–13–7, 1–10–3–11–5–13–7, 1–11–5–13–13–7, 1–11–5–10–3–13–7, y todos los subtítulos de éstos a partir de 1. El set ${\displaystyle Z}$ por lo tanto {1,3,5,7,10,11,13}, resultando en ${\displaystyle L\setminus Z=\{2,4,6\}$, ${\displaystyle R\cap Z=\{10,11,13}$ y la cubierta mínima de vértice ${\displaystyle K=\{2,4,6,10,11,13}$.

Para los grafos que no son bipartitos, la cobertura mínima de vértices puede ser mayor que la correspondencia máxima. Además, los dos problemas son muy diferentes en complejidad: las correspondencias máximas se pueden encontrar en tiempo polinómico para cualquier grafo, mientras que la cobertura mínima de vértices es NP-completa.

El complemento de una cobertura de vértices en cualquier grafo es un conjunto independiente, por lo que una cobertura de vértices mínima es complementaria a un conjunto independiente máximo; encontrar conjuntos independientes máximos es otro problema NP-completo. La equivalencia entre emparejamiento y cobertura articulada en el teorema de König permite calcular coberturas de vértices mínimas y conjuntos independientes máximos en tiempo polinomial para grafos bipartitos, a pesar de la NP-completitud de estos problemas para familias de grafos más generales.

El teorema de Kőnig recibe su nombre del matemático húngaro Dénes Kőnig. Kőnig había anunciado en 1914 y publicado en 1916 los resultados de que todo grafo bipartito regular tiene una correspondencia perfecta y, de manera más general, que el índice cromático de cualquier grafo bipartito (es decir, el número mínimo de correspondencias en las que se puede dividir) es igual a su grado máximo; esta última afirmación se conoce como teorema de coloración de líneas de Kőnig. Sin embargo, Bondy y Murty (1976) atribuyen el propio teorema de Kőnig a un artículo posterior de Kőnig (1931).

Según Biggs, Lloyd & Wilson (1976), Kőnig atribuyó la idea de estudiar los emparejamientos en grafos bipartitos a su padre, el matemático Gyula Kőnig. En húngaro, el nombre de Kőnig tiene doble acento agudo, pero su teorema a veces se escribe (incorrectamente) en caracteres alemanes, con diéresis.

El teorema de König es equivalente a muchos otros teoremas de min-max en teoría de grafos y combinatoria, como el teorema del matrimonio de Hall y el teorema de Dilworth. Dado que la correspondencia bipartita es un caso especial de flujo máximo, el teorema también resulta del teorema de corte mínimo de flujo máximo.

Se dice que un grafo es perfecto si, en cada subgrafo inducido, el número cromático es igual al tamaño del grupo más grande. Cualquier grafo bipartito es perfecto, porque cada uno de sus subgrafos es bipartito o independiente; en un grafo bipartito que no es independiente, el número cromático y el tamaño del grupo más grande son ambos dos, mientras que en un conjunto independiente, el número cromático y el número del grupo son ambos uno.

Un grafo es perfecto si y solo si su complemento es perfecto, y el teorema de König puede verse como equivalente a la afirmación de que el complemento de un grafo bipartito es perfecto. Porque, cada clase de color en una coloración del complemento de un grafo bipartito tiene un tamaño de como máximo 2 y las clases de tamaño 2 forman una correspondencia, una camarilla en el complemento de un grafo G es un conjunto independiente en G, y como ya hemos descrito un conjunto independiente en un grafo bipartito G es un complemento de una cubierta de vértices en G. Por lo tanto, cualquier correspondencia M en un grafo bipartito G con n vértices corresponde a una coloración del complemento de G con n-|M| colores, que por la perfección de los complementos de los grafos bipartitos corresponde a un conjunto independiente en G con n-|M| vértices, que corresponde a una cubierta de vértices de G con M vértices. Por el contrario, el teorema de König demuestra la perfección de los complementos de los grafos bipartitos, resultado demostrado de forma más explícita por Gallai (1958).

También se puede conectar el teorema de coloración de líneas de König con una clase diferente de grafos perfectos, los grafos de líneas de grafos bipartitos. Si G es un grafo, el grafo de líneas L(G) tiene un vértice para cada arista de G, y una arista para cada par de aristas adyacentes en G. Por lo tanto, el número cromático de L(G) es igual al índice cromático de G. Si G es bipartito, las camarillas en L(G) son exactamente los conjuntos de aristas en G que comparten un punto final común. Ahora bien, el teorema de coloración de líneas de König, que establece que el índice cromático es igual al grado máximo del vértice en cualquier grafo bipartito, puede interpretarse como que el grafo de líneas de un grafo bipartito es perfecto.

Dado que los gráficos lineales de los grafos bipartitos son perfectos, los complementos de los gráficos lineales de los grafos bipartitos también son perfectos. Una camarilla en el complemento del gráfico lineal de G es simplemente una coincidencia en G. Y una coloración en el complemento del gráfico lineal de G, cuando G es bipartito, es una partición de las aristas de G en subconjuntos de aristas que comparten un punto final común; los puntos finales compartidos por cada uno de estos subconjuntos forman una cubierta de vértices para G. Por lo tanto, el propio teorema de König también puede interpretarse como que afirma que los complementos de los gráficos lineales de los grafos bipartitos son perfectos.

El teorema de Konig se puede extender a los gráficos ponderados.

Jenő Egerváry (1931) consideró grafos en los que cada arista e tiene un peso entero no negativo w_e. El vector de pesos se denota por w. El w-peso de un emparejamiento es la suma de los pesos de las aristas que participan en el emparejamiento. Un w-cobertura de vértices es un multiconjunto de vértices ("multiconjunto" significa que cada vértice puede aparecer varias veces), en el que cada arista e es adyacente a al menos w_e vértices. El teorema de Egerváry dice:

En cualquier gráfico bipartito ponderado, el máximo w-peso de un emparejado equivale al menor número de vértices en un w-Cubierta de vértice.

El peso máximo w- de una correspondencia fraccionaria viene dado por el LP:

Maximizar w · x

Sujeto a: x ≥ 0_E

_______ A_G · x ≤ 1_V.

Y el número mínimo de vértices en una w-cubierta de vértices fraccionaria está dado por el LP dual:

Minimize 1_V · Sí.

Sujeto a: Sí. ≥ 0_V

_______ A_G^T · Sí. ≥ w.

Al igual que en la prueba del teorema de Konig, el teorema de dualidad LP implica que los valores óptimos son iguales (para cualquier gráfico), y el hecho de que el gráfico sea bipartito implica que estos programas tienen soluciones óptimas en las que todos los valores son números enteros.

Se puede considerar un grafo en el que cada vértice v tiene un peso entero no negativo b_v. El vector de pesos se denota por b. El b-peso de una cubierta de vértices es la suma de b_v para todos los v en la cubierta. Una b-coincidencia es una asignación de un peso entero no negativo a cada arista, de modo que la suma de los pesos de las aristas adyacentes a cualquier vértice v sea como máximo b_v. El teorema de Egerváry se puede extender, utilizando un argumento similar, a grafos que tienen pesos de arista w y pesos de vértice b:

En cualquier gráfico bipartito ponderado en el borde, el máximo w-peso de un b-iguiendo igual al mínimo b- peso de vértices en un w-Cubierta de vértice.

• Propiedad de Kőnig en hipergraphs

• Biggs, E. K.; Lloyd; Wilson, R. J. (1976), Graph Theory 1736–1936, Oxford University Press, pp. 203–207, ISBN 0-19-853916-9.
• Cesa-Bianchi, Nicolò (11 de abril de 2020), Matchings y el max-flow min-cut theorem (PDF)
• Cook, William J.; Cunningham, William H.; Pulleyblank, William R.; Schrijver, Alexander (2011), Optimización Combinatorial, Wiley Series in Discrete Mathematics and Optimization, vol. 33, John Wiley & Sons, pp. 48–49, ISBN 9781118031391.
• Bondy, J. A.; Murty, U. S. R. (1976), Teoría de Gráfico con Aplicaciones, Holanda septentrional, ISBN 0-444-19451-7.
• Gallai, Tibor (1958), "Maximum-minimum Sätze über Graphen", Acta Mathematica Academiae Scientiarum Hungaricae, 9 (3–4): 395–434, doi:10.1007/BF02020271, MR 0124238.
• Gös, Mika; Suomela, Jukka (2014), "No hay esquema de aproximación sublogarítmica para la cubierta bipartita del vértice", Computación distribuida, 27 (6): 435-443, arXiv:1205.4605, doi:10.1007/s00446-013-0194-z, MR 3280546, S2CID 13513566
• Kőnig, Dénes (1916), "Gráfok és alkalmazásuk a determinánsok és a halmazok elméletére", Matematikai és Természettudományi Értesítő, 34: 104–119.
• Kőnig, Dénes (1931), "Gráfok és mátrixok", Matematikai és Fizikai Lapok, 38: 116–119.
• Lovász, László (1972), "Hipergrafías normales y la conjetura perfecta del gráfico", Discreta matemáticas, 2 (3): 253–267, doi:10.1016/0012-365X(72)90006-4, MR 0302480.
• Lovász, László (1974), "Minimax theorems for hypergraphs", Seminario Hypergraph (Proc. First Working Sem., Ohio State Univ., Columbus, Ohio, 1972; dedicado a Arnold Ross), Notas de conferencias en matemáticas, vol. 411, Berlín: Springer, pp. 111–126, doi:10.1007/BFb0066186, ISBN 978-3-540-06846-4, MR 0406862.
• Lovász, László; Plummer, M. D. (1986), Coincidiendo Teoría, Annals of Discrete Mathematics, vol. 29, North-Holland, ISBN 0-444-87916-1, MR 0859549
• Storer, J. A. (2001), Introducción a estructuras de datos y algoritmos, Progresos en la Ciencia de la Computación y Serie Lógica Aplicada, Springer, ISBN 9780817642532.