Teorema de campana

Teorema de Bell es un término que abarca una serie de resultados estrechamente relacionados en la física, todos los cuales determinan que la mecánica cuántica es incompatible con las teorías locales de variables ocultas dadas algunas suposiciones básicas sobre la naturaleza de la medida. "Locales" aquí se refiere al principio de localidad, la idea de que una partícula solo puede ser influenciada por su entorno inmediato, y que las interacciones mediadas por campos físicos solo pueden ocurrir a velocidades no mayores que la velocidad de la luz. "Variables ocultas" son propiedades hipotéticas que poseen las partículas cuánticas, propiedades que son indetectables pero que aún afectan el resultado de los experimentos. En palabras del físico John Stewart Bell, por quien se nombra esta familia de resultados, "Si [una teoría de variables ocultas] es local, no estará de acuerdo con la mecánica cuántica, y si está de acuerdo con la mecánica cuántica, no lo estará". ser local."

El término se aplica ampliamente a varias derivaciones diferentes, la primera de las cuales fue presentada por Bell en un artículo de 1964 titulado "Sobre la paradoja de Einstein Podolsky Rosen". El artículo de Bell fue una respuesta a un experimento mental de 1935 que propusieron Albert Einstein, Boris Podolsky y Nathan Rosen, argumentando que la física cuántica es una ciencia 'incompleta'. teoría. Para 1935 ya se reconocía que las predicciones de la física cuántica son probabilísticas. Einstein, Podolsky y Rosen presentaron un escenario que implica preparar un par de partículas de modo que el estado cuántico del par se enrede y luego separar las partículas a una distancia arbitrariamente grande. El experimentador puede elegir entre las posibles medidas que se pueden realizar en una de las partículas. Cuando eligen una medida y obtienen un resultado, el estado cuántico de la otra partícula aparentemente colapsa instantáneamente en un nuevo estado dependiendo de ese resultado, sin importar qué tan lejos esté la otra partícula. Esto sugiere que la medición de la primera partícula de alguna manera también interactuó con la segunda partícula a una velocidad superior a la de la luz, o que las partículas entrelazadas tenían alguna propiedad no medida que predeterminaba sus estados cuánticos finales antes fueron separados. Por lo tanto, asumiendo la localidad, la mecánica cuántica debe ser incompleta, ya que no puede dar una descripción completa de las verdaderas características físicas de la partícula. En otras palabras, las partículas cuánticas, como los electrones y los fotones, deben tener algunas propiedades o atributos no incluidos en la teoría cuántica, y las incertidumbres en las predicciones de la teoría cuántica se deberían entonces a la ignorancia o falta de conocimiento de estas propiedades, más tarde denominadas & #34;variables ocultas".

Bell llevó el análisis del entrelazamiento cuántico mucho más lejos. Dedujo que si las mediciones se realizan de forma independiente en las dos partículas separadas de un par entrelazado, entonces la suposición de que los resultados dependen de variables ocultas dentro de cada mitad implica una restricción matemática sobre cómo se correlacionan los resultados de las dos mediciones. Esta restricción más tarde se llamaría la desigualdad de Bell. Bell luego mostró que la física cuántica predice correlaciones que violan esta desigualdad. En consecuencia, la única forma en que las variables ocultas podrían explicar las predicciones de la física cuántica es si son 'no locales', lo que quiere decir que, de alguna manera, las dos partículas pudieron interactuar instantáneamente sin importar qué tan lejos estén las dos partículas. apartado.

En los años siguientes se propusieron múltiples variaciones del teorema de Bell, que introdujeron otras condiciones estrechamente relacionadas, generalmente conocidas como desigualdades de Bell (o "tipo Bell"). El primer experimento rudimentario diseñado para probar el teorema de Bell fue realizado en 1972 por John Clauser y Stuart Freedman. Experimentos más avanzados, conocidos colectivamente como pruebas de Bell, se han realizado muchas veces desde entonces. A menudo, estos experimentos han tenido el objetivo de 'cerrar lagunas', es decir, mejorar los problemas de diseño o configuración experimental que, en principio, podrían afectar la validez de los resultados de las pruebas de Bell anteriores. Hasta la fecha, las pruebas de Bell han encontrado consistentemente que los sistemas físicos obedecen a la mecánica cuántica y violan las desigualdades de Bell; lo que quiere decir que los resultados de estos experimentos son incompatibles con cualquier teoría de variable oculta local.

Físicos y filósofos han debatido la naturaleza exacta de las suposiciones requeridas para demostrar una restricción tipo Bell sobre las correlaciones. Si bien la importancia del teorema de Bell no está en duda, sus implicaciones completas para la interpretación de la mecánica cuántica siguen sin resolverse.

Teorema

Hay muchas variaciones sobre la idea básica, algunas emplean suposiciones matemáticas más sólidas que otras. Significativamente, los teoremas tipo Bell no se refieren a ninguna teoría particular de variables ocultas locales, sino que muestran que la física cuántica viola los supuestos generales detrás de las imágenes clásicas de la naturaleza. El teorema original demostrado por Bell en 1964 no es el más susceptible de experimentar, y es conveniente introducir el género de las desigualdades tipo Bell con un ejemplo posterior.

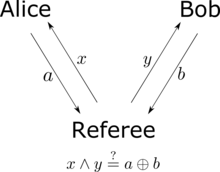
Los personajes hipotéticos Alice y Bob están en lugares muy separados. Su colega Victor prepara un par de partículas y envía una a Alice y la otra a Bob. Cuando Alice recibe su partícula, decide realizar una de las dos medidas posibles (quizás volteando una moneda para decidir cuál). Denote estas mediciones por A0{displaystyle A_{0} y A1{displaystyle A_{1}. Ambos A0{displaystyle A_{0} y A1{displaystyle A_{1} son binario medidas: el resultado de A0{displaystyle A_{0} o +1{displaystyle +1} o − − 1{displaystyle -1}, y también para A1{displaystyle A_{1}. Cuando Bob recibe su partícula, elige una de dos medidas, B0{displaystyle B_{0} y B1{displaystyle B_{1}, que también son binarios.

Supongamos que cada medición revela una propiedad que la partícula ya poseía. Por ejemplo, si Alice decide medir A0{displaystyle A_{0} y obtiene el resultado +1{displaystyle +1}, entonces la partícula que recibió llevó un valor +1{displaystyle +1} para una propiedad a0{displaystyle A_{0}. Considere la siguiente combinación:

a0b0+a0b1+a1b0− − a1b1=()a0+a1)b0+()a0− − a1)b1.{displaystyle a_{0}b_{0}a_{0}+a_{1}b_{0}-a_{1}b_{1}=(a_{0}+a_{1})b_{0}+(a_{0}-a_{0}-a_{1})b_{1}},}}}

Porque ambos a0{displaystyle A_{0} y a1{displaystyle A_{1} tomar los valores ± ± 1{displaystyle pm 1}, entonces a0=a1{displaystyle A_{0}=a_{1} o a0=− − a1{displaystyle A_{0}=-a_{1}. En el caso anterior, ()a0− − a1)b1=0{displaystyle (a_{0}-a_{1}b_{1}=0}, mientras que en el último caso, ()a0+a1)b0=0{displaystyle (a_{0}+a_{1}b_{0}=0}. Entonces, uno de los términos de la mano derecha de la expresión anterior desaparecerá, y el otro igualará ± ± 2{displaystyle pm 2}. En consecuencia, si el experimento se repite en muchos ensayos, con Víctor preparando nuevos pares de partículas, el valor promedio de la combinación a0b0+a0b1+a1b0− − a1b1{displaystyle a_{0}b_{0}-a_{0}b_{1}a_{0}-a_{1}b_{1}b_{1} en todos los juicios será inferior o igual a 2. No single la prueba puede medir esta cantidad, ya que Alice y Bob sólo pueden elegir una medida cada uno, pero en el supuesto de que las propiedades subyacentes existen, el valor promedio de la suma es sólo la suma de los promedios para cada término. Usando soportes de ángulo para denotar promedios,

.. A0B0.. +.. A0B1.. +.. A1B0.. − − .. A1B1.. ≤ ≤ 2.{displaystyle langle A_{0}B_{0}rangle +langle A_{0}B_{1}rangle +langle A_{1}B_{0}rangle -langle A_{1}B_{1}rangle leq 2,.}

a0,a1,b0,{displaystyle a_{0},a_{1},b_{0}

b1{displaystyle B_{1}

La mecánica cuántica puede violar la desigualdad CHSH, de la siguiente manera. Víctor prepara un par de qubits que describe por el estado de Bell

Silencio↑ ↑ .. =Silencio0.. ⊗ ⊗ Silencio1.. − − Silencio1.. ⊗ ⊗ Silencio0.. 2,{displaystyle tenciónpsi rangle ={frac { actual0rangle otimes tención1rangle - duración1rangle otimes tención0rangle }{sqrt {2}}}}

Silencio0.. {displaystyle Silencioso

Silencio1.. {displaystyle ← }

σ σ z=()100− − 1).{displaystyle sigma {fnMicrosoft Sans Serif}

σ σ z{displaystyle sigma _{z}

σ σ x{displaystyle sigma _{x}

A0=σ σ z,A1=σ σ x=()0110);{displaystyle A_{0}=sigma _{z}, A_{1}=sigma - ¿Por qué?

B0=− − σ σ x+σ σ z2,B1=σ σ x− − σ σ z2.{displaystyle B_{0}=-{frac {sigma _{x}+sigma _{z}{sqrt {2} B_{1}={frac} {sigma ¿Por qué? {2}}}

.. A0⊗ ⊗ B0.. =12,.. A0⊗ ⊗ B1.. =12,.. A1⊗ ⊗ B0.. =12,.. A1⊗ ⊗ B1.. =− − 12.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}

.. A0⊗ ⊗ B0.. +.. A0⊗ ⊗ B1.. +.. A1⊗ ⊗ B0.. − − .. A1⊗ ⊗ B1.. =22{displaystyle langle A_{0}otimes B_{0}rangle +langle A_{0}otimes B_{1}rangle +langle A_{1}otimes B_{0}rangle -langle A_{1}otimes B_{1}rangle =2{sqrt {2}

22{displaystyle 2{sqrt {2}}

Una ilustración del juego CHSH: el árbitro, Victor, envía un poco cada uno a Alice y a Bob, y Alice y Bob cada uno envía un poco de vuelta al árbitro.

La desigualdad CHSH también se puede considerar como un juego en el que Alice y Bob tratan de coordinar sus acciones. Víctor prepara dos pedazos, x{displaystyle x} y Sí.{displaystyle y}, independientemente y al azar. Él envía un poco x{displaystyle x} a Alice y poco Sí.{displaystyle y} Alice y Bob ganan si regresan los bits de respuesta a{displaystyle a} y b{displaystyle b} a Víctor, satisfacción

xSí.=a+bmod2.{displaystyle xy=a+bmod 2,}

x{displaystyle x}

Sí.{displaystyle y}

a{displaystyle a}

b{displaystyle b}

3/4{displaystyle 3/4}

2+24.. 0.85.{fnMicroc} {2+{sqrt {2}} {4}approx 0.85,}

Variaciones y resultados relacionados

Campana (1964)

El papel de Bell en 1964 señala que bajo condiciones restringidas, los modelos variables locales ocultos pueden reproducir las predicciones de la mecánica cuántica. Él entonces demuestra que esto no puede ser verdad en general. Bell considera un refinamiento por David Bohm del experimento de pensamiento Einstein-Podolsky-Rosen (EPR). En este escenario, un par de partículas se forman juntas de tal manera que son descritas por un estado de soltero de giro (que es un ejemplo de un estado enredado). Las partículas se alejan en direcciones opuestas. Cada partícula se mide por un dispositivo Stern-Gerlach, un instrumento de medición que puede orientarse en diferentes direcciones y que reporta uno de dos posibles resultados, representable por +1{displaystyle +1} y − − 1{displaystyle -1}. La configuración de cada instrumento de medición está representada por un vector unitario, y la predicción cuántica-mecánica para la correlación entre dos detectores con ajustes a→ → {displaystyle {vec}} y b→ → {displaystyle {vec}} es

P()a→ → ,b→ → )=− − a→ → ⋅ ⋅ b→ → .{displaystyle P({vec {}},{vec {b})=-{vec {}cdot {vec {b},}

En particular, si la orientación de los dos detectores es la misma (a→ → =b→ → {displaystyle {vec {a}={vec} {b}}), entonces el resultado de una medición es seguro que es el negativo del resultado de la otra, dando P()a→ → ,a→ → )=− − 1{displaystyle P({vec},{vec {a}}=-1}. Y si las orientaciones de los dos detectores son ortogonales (a→ → ⋅ ⋅ b→ → =0{displaystyle {vec}cdot {vec}=0}), entonces los resultados no están relacionados, y P()a→ → ,b→ → )=0{displaystyle P({vec},{vec {b}=0}. Bell demuestra por ejemplo que estos casos especiales puede se explica en términos de variables ocultas, luego procede a demostrar que la gama completa de posibilidades que implican ángulos intermedios No puedo.

Bell posited that a local hidden variable model for these correlations would explain them in terms of an integral over the possible values of some hidden parameter λ λ {displaystyle lambda }:

P()a→ → ,b→ → )=∫ ∫ dλ λ *** *** ()λ λ )A()a→ → ,λ λ )B()b→ → ,λ λ ),{displaystyle P({vec {}},{vec {b})=int dlambda ,rho (lambda)A({vec {a},lambda)B({vec {b},lambda),}

*** *** ()λ λ ){displaystyle rho (lambda)}

A()a→ → ,λ λ ){displaystyle A({vec {}},lambda)}

B()b→ → ,λ λ ){displaystyle B({vec {b},lambda)}

A()a→ → ,λ λ )=± ± 1,B()b→ → ,λ λ )=± ± 1.{displaystyle A({vec {}},lambda)=pm 1,,B({vec {b},lambda)=pm 1,}

A{displaystyle A}

b→ → {displaystyle {vec}}

B{displaystyle B}

a→ → {displaystyle {vec}}

b→ → {displaystyle {vec}}

c→ → {displaystyle {vec}}

SilencioP()a→ → ,b→ → )− − P()a→ → ,c→ → )Silencio≤ ≤ 1+P()b→ → ,c→ → ).{displaystyle SilencioP({vec {a}},{vec {b})-P({vec {a}},{vec {c}}) Portadaleq 1+P({vec {b},{vec {}),},}

a→ → {displaystyle {vec}}

b→ → {displaystyle {vec}}

c→ → {displaystyle {vec}}

P()a→ → ,b→ → )=0,{fnMicrosoft Sans Serif}

P()a→ → ,c→ → )=P()b→ → ,c→ → )=− − 22,{displaystyle P({vec {}},{vec {c})=P({vec {b},{vec {}}})=-{frac {sqrt {2}{2},}

22≰ ≰ 1− − 22.{displaystyle {frac {sqrt {2}{2}nleq 1-{frac {sqrt {2}{2},}

a→ → {displaystyle {vec}}

b→ → {displaystyle {vec}}

c→ → {displaystyle {vec}}

El teorema de Bell de 1964 requiere la posibilidad de anticorrelaciones perfectas: la capacidad de hacer una predicción de probabilidad 1 sobre el resultado del segundo detector, conociendo el resultado del primero. Esto está relacionado con el "criterio EPR de realidad", un concepto introducido en el artículo de 1935 de Einstein, Podolsky y Rosen. Este artículo postula: "Si, sin perturbar de ningún modo un sistema, podemos predecir con certeza (es decir, con probabilidad igual a la unidad) el valor de una cantidad física, entonces existe un elemento de realidad que corresponde a esa cantidad".."

GHZ–Mermín (1990)

Daniel Greenberger, Michael A. Horne y Anton Zeilinger presentaron un experimento mental de cuatro partículas en 1990, que luego David Mermin simplificó para usar solo tres partículas. En este experimento mental, Victor genera un conjunto de tres partículas de espín-1/2 descritas por el estado cuántico

Silencio↑ ↑ .. =12()Silencio000.. − − Silencio111.. ),{displaystyle Нpsi rangle ={frac {1}{sqrt {2}}}(Prince000rangle - resist111rangle),}

Silencio0.. {displaystyle Silencioso

Silencio1.. {displaystyle ← }

σ σ z{displaystyle sigma _{z}

σ σ x{displaystyle sigma _{x}

σ σ Sí.{displaystyle sigma _{y}

+1{displaystyle +1}

− − 1{displaystyle -1}

Silencio↑ ↑ .. {displaystyle TENED rangle }

σ σ x{displaystyle sigma _{x}

σ σ Sí.{displaystyle sigma _{y}

+1{displaystyle +1}

Silencio↑ ↑ .. {displaystyle TENED rangle }

σ σ x⊗ ⊗ σ σ Sí.⊗ ⊗ σ σ Sí.{displaystyle sigma _{x}otimes sigma _{y}otimes sigma _{y}

+1{displaystyle +1}

σ σ Sí.⊗ ⊗ σ σ x⊗ ⊗ σ σ Sí.{displaystyle sigma _{y}otimes sigma _{x}otimes sigma _{y}

σ σ Sí.⊗ ⊗ σ σ Sí.⊗ ⊗ σ σ x{displaystyle sigma _{y}otimes sigma _{y}otimes sigma _{x}

σ σ x{displaystyle sigma _{x}

σ σ Sí.{displaystyle sigma _{y}

σ σ Sí.{displaystyle sigma _{y}

σ σ Sí.{displaystyle sigma _{y}

σ σ x{displaystyle sigma _{x}

σ σ Sí.{displaystyle sigma _{y}

()ax,aSí.,bx,bSí.,cx,cSí.),{displaystyle (a_{x},a_{y},b_{x},b_{y},c_{x},c_{y}),}

− − 1{displaystyle -1}

+1{displaystyle +1}

σ σ x{displaystyle sigma _{x}

σ σ Sí.{displaystyle sigma _{y}

Si Alice, Bob y Charlie realizan todo σ σ x{displaystyle sigma _{x} medición, entonces el producto de sus resultados sería axbxcx{displaystyle A_{x}b_{x}c_{x}}. Este valor se puede deducir

()axbSí.cSí.)()aSí.bxcSí.)()aSí.bSí.cx)=axbxcxaSí.2bSí.2cSí.2=axbxcx,{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {c_} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {c} {c} {c}}}}}} {c_c_c_c_c_c_c_c_c_c_c_cc_c_cccccccccccccccccccccccc_ccccccccccccccccccccccccccccc}

− − 1{displaystyle -1}

+1{displaystyle +1}

1{displaystyle 1}

+1{displaystyle +1}

axbxcx=+1,{displaystyle a_{x}b_{x}c_{x}=+1,}

+1{displaystyle +1}

Silencio↑ ↑ .. {displaystyle TENED rangle }

σ σ x⊗ ⊗ σ σ x⊗ ⊗ σ σ x{displaystyle sigma _{x}otimes sigma _{x}otimes sigma _{x}

− − 1{displaystyle -1}

Este experimento de pensamiento también puede ser retransmitido como tradicional La desigualdad de Bell o, equivalentemente, como un juego no local en el mismo espíritu que el juego CHSH. En él, Alice, Bob y Charlie reciben pedacitos x,Sí.,z{displaystyle x,y,z} de Víctor, prometida tener siempre un número de ellos, es decir, x⊕ ⊕ Sí.⊕ ⊕ z=0{displaystyle xoplus yoplus z=0}, y enviarle de vuelta bits a,b,c{displaystyle a,b,c}. Ganan el juego si a,b,c{displaystyle a,b,c} tienen un número extraño de los para todas las entradas excepto x=Sí.=z=0{displaystyle x=y=z=0}, cuando necesitan tener un número uniforme de ellos. Es decir, ellos ganan el juego sif a⊕ ⊕ b⊕ ⊕ c=xAlternativa Alternativa Sí.Alternativa Alternativa z{displaystyle aoplus boplus c=xlor ylor z}. Con variables ocultas locales la mayor probabilidad de victoria que pueden tener es de 3/4, mientras que usando la estrategia cuántica por encima de ellos ganan con certeza. Este es un ejemplo de pseudo-telepatía cuántica.

Teorema de Kochen-Specker (1967)

En teoría cuántica, las bases ortonormales para un espacio Hilbert representan mediciones que se pueden realizar en un sistema que tiene ese espacio Hilbert. Cada vector en una base representa un posible resultado de esa medición. Supongamos que una variable oculta λ λ {displaystyle lambda } existe, por lo que saber el valor λ λ {displaystyle lambda } implicaría certeza sobre el resultado de cualquier medición. Dado un valor λ λ {displaystyle lambda }, cada resultado de medición —es decir, cada vector en el espacio Hilbert— es imposible o garantizado. Una configuración de Kochen-Specker es un conjunto finito de vectores hechos de múltiples bases entrelazadas, con la propiedad de que un vector en él siempre será imposible cuando se considera que pertenece a una base y garantizado cuando se toma como perteneciente a otro. En otras palabras, una configuración de Kochen-Specker es un "conjunto incoloro" que demuestra la inconsistencia de asumir una variable oculta λ λ {displaystyle lambda } puede controlar los resultados de medición.

Teorema del libre albedrío

El tipo de argumento Kochen-Specker, utilizando configuraciones de bases interconectadas, se puede combinar con la idea de medir pares enredados que subyacen a desigualdades tipo Bell. Esto fue notado a partir de los años 70 por Kochen, Heywood y Redhead, Stairs, y Brown y Svetlichny. Como señaló EPR, obtener un resultado de medición en la mitad de un par enredado implica certeza sobre el resultado de una medición correspondiente en la otra mitad. El criterio de la EPR de la realidad plantea que porque la segunda mitad del par no fue perturbada, esa certeza debe ser debida a una propiedad física que le pertenece. En otras palabras, por este criterio, una variable oculta λ λ {displaystyle lambda } debe existir dentro de la segunda, la mitad no asegurada de la pareja. No surge contradicción si sólo se considera una medida en la primera mitad. Sin embargo, si el observador tiene una selección de múltiples mediciones posibles, y los vectores que definen esas mediciones forman una configuración de Kochen-Specker, entonces algún resultado en la segunda mitad será simultáneamente imposible y garantizado.

Este tipo de argumento llamó la atención cuando John Conway y Simon Kochen presentaron un ejemplo bajo el nombre de teorema del libre albedrío. El teorema de Conway-Kochen utiliza un par de qutrits entrelazados y una configuración de Kochen-Specker descubierta por Asher Peres.

Entrelazamiento cuasiclásico

Como señaló Bell, algunas predicciones de la mecánica cuántica se pueden replicar en modelos de variables ocultas locales, incluidos casos especiales de correlaciones producidas por entrelazamiento. Este tema ha sido estudiado sistemáticamente en los años posteriores al teorema de Bell. En 1989, Reinhard Werner introdujo lo que ahora se denominan estados de Werner, estados cuánticos conjuntos para un par de sistemas que generan correlaciones de tipo EPR pero que también admiten un modelo de variables ocultas. Los estados de Werner son estados cuánticos bipartitos que son invariantes bajo unitarios de forma de producto tensorial simétrico:

*** *** AB=()U⊗ ⊗ U)*** *** AB()U† † ⊗ ⊗ U† † ).{displaystyle rho _{AB}=(Uotimes U)rho _{AB}(U^{dagger }otimes U^{dagger }),}

En 2004, Robert Spekkens introdujo un modelo de juguete que comienza con la premisa de grados de libertad discretizados locales y luego impone un "principio de equilibrio de conocimiento" eso restringe cuánto puede saber un observador sobre esos grados de libertad, convirtiéndolos así en variables ocultas. Los estados de conocimiento permitidos ('estados epistémicos') sobre las variables subyacentes ('estados ónticos') imitan algunas características de los estados cuánticos. Las correlaciones en el modelo de juguete pueden emular algunos aspectos del enredo, como la monogamia, pero por construcción, el modelo de juguete nunca puede violar una desigualdad de Bell.

Historia

Antecedentes

La cuestión de si la mecánica cuántica se puede "completar" por variables ocultas data de los primeros años de la teoría cuántica. En su libro de texto de 1932 sobre mecánica cuántica, el erudito de origen húngaro John von Neumann presentó lo que afirmó ser una prueba de que no podía haber "parámetros ocultos". La validez y el carácter definitivo de la prueba de von Neumann fueron cuestionados por Hans Reichenbach, con más detalle por Grete Hermann, y posiblemente en una conversación, aunque no impresa, por Albert Einstein. (Simon Kochen y Ernst Specker rechazaron la suposición clave de von Neumann ya en 1961, pero no publicaron una crítica hasta 1967).

Einstein argumentó persistentemente que la mecánica cuántica no podía ser una teoría completa. Su argumento preferido se basaba en un principio de localidad:

Considerar un sistema mecánico constituido por dos sistemas parciales A y B que tienen interacción entre sí sólo durante el tiempo limitado. Deje que la función  antes de su interacción sea dada. Luego la ecuación Schrödinger proporcionará la función  después de su interacción ha tenido lugar. Vamos a determinar ahora la condición física del sistema parcial A lo más posible por las mediciones. Entonces la mecánica cuántica nos permite determinar la función  B de las mediciones realizadas, y de la función ↑ del sistema total. Sin embargo, esta determinación da un resultado que depende de que de las magnitudes determinantes especificando la condición A se ha medido (por ejemplo, coordenadas o momenta). Puesto que sólo puede haber uno estado físico B después de la interacción y que razonablemente no puede considerarse como dependiente de la medida particular que realizamos en el sistema A separados B se puede llegar a la conclusión de que la función ↑ no está coordinada inequívocamente con la condición física. Esta coordinación de varias funciones  con la misma condición física del sistema B muestra de nuevo que la función  no puede ser interpretada como una descripción (completa) de una condición física de un sistema unitario.

El experimento mental EPR es similar, también considera dos sistemas separados A y B descritos por una función de onda conjunta. Sin embargo, el documento EPR agrega la idea más tarde conocida como el criterio de realidad EPR, según el cual la capacidad de predecir con probabilidad 1 el resultado de una medición sobre B implica la existencia de un " elemento de la realidad" dentro de B.

En 1951, David Bohm propuso una variante del experimento mental EPR en el que las mediciones tienen rangos discretos de posibles resultados, a diferencia de las mediciones de posición y momento consideradas por EPR. El año anterior, Chien-Shiung Wu e Irving Shaknov habían medido con éxito las polarizaciones de los fotones producidos en pares entrelazados, lo que hizo que la versión de Bohm del experimento mental EPR fuera prácticamente factible.

A fines de la década de 1940, el matemático George Mackey se interesó por los fundamentos de la física cuántica y en 1957 redactó una lista de postulados que consideró una definición precisa de la mecánica cuántica. Mackey conjeturó que uno de los postulados era redundante y, poco después, Andrew M. Gleason demostró que, de hecho, era deducible de los otros postulados. El teorema de Gleason proporcionó un argumento de que una amplia clase de teorías de variables ocultas son incompatibles con la mecánica cuántica. Más específicamente, el teorema de Gleason descarta los modelos de variables ocultas que son "no contextuales". Cualquier modelo de variables ocultas para la mecánica cuántica debe, para evitar las implicaciones del teorema de Gleason, involucrar variables ocultas que no son propiedades que pertenecen solo al sistema medido, sino que también dependen del contexto externo en el que se realiza la medición.. Este tipo de dependencia a menudo se considera artificial o indeseable; en algunos entornos, es inconsistente con la relatividad especial. El teorema de Kochen-Specker refina esta declaración al construir un subconjunto finito específico de rayos en el que no se puede definir tal medida de probabilidad.

Tsung-Dao Lee estuvo cerca de derivar el teorema de Bell en 1960. Consideró eventos en los que se producían dos kaones que viajaban en direcciones opuestas y llegó a la conclusión de que las variables ocultas no podían explicar las correlaciones que se podían obtener. en tales situaciones. Sin embargo, surgieron complicaciones debido al hecho de que los kaones decaen, y no fue tan lejos como para deducir una desigualdad tipo Bell.

Publicaciones de Bell

Bell eligió publicar su teorema en una revista comparativamente desconocida porque no requería cargos por página y, en ese momento, de hecho pagaba a los autores que publicaban allí. Sin embargo, debido a que la revista no proporcionó reimpresiones gratuitas de los artículos para que los autores las distribuyeran, Bell tuvo que gastar el dinero que recibió para comprar copias que pudiera enviar a otros físicos. Si bien los artículos impresos en la revista enumeraban el nombre de la publicación simplemente como Physics, las portadas tenían la versión trilingüe Physics Physique Физика para reflejar que imprimiría artículos en inglés, francés y ruso.

Antes de demostrar su resultado de 1964, Bell también demostró un resultado equivalente al teorema de Kochen-Specker (por lo tanto, este último a veces también se conoce como teorema de Bell-Kochen-Specker o Bell-KS). Sin embargo, la publicación de este teorema se retrasó inadvertidamente hasta 1966. En ese artículo, Bell argumentó que debido a que una explicación de los fenómenos cuánticos en términos de variables ocultas requeriría la no localidad, la paradoja EPR "se resuelve en la forma en que Einstein habría me gustó menos".

Experimentos

Esquema de un "dos canales" Prueba de Bell
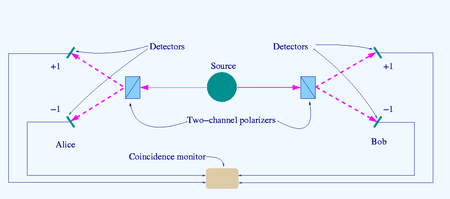
La fuente S produce pares de "fotones", enviados en direcciones opuestas. Cada foton encuentra un polarizador de dos canales cuya orientación (a o b) puede ser establecida por el experimentador. Se detectan señales emergentes de cada canal y las coincidencias de cuatro tipos (+++, −, +− y −+) contadas por el monitor de coincidencia.

En 1967, el título inusual Physics Physique Физика llamó la atención de John Clauser, quien luego descubrió el artículo de Bell y comenzó a considerar cómo realizar una prueba de Bell en el laboratorio. Clauser y Stuart Freedman continuaron realizando una prueba de Bell en 1972. Esta fue solo una prueba limitada, porque la elección de la configuración del detector se realizó antes de que los fotones abandonaran la fuente. En 1982, Alain Aspect y colaboradores realizaron la primera prueba de Bell para eliminar esta limitación. Esto inició una tendencia de pruebas de Bell progresivamente más estrictas. El experimento mental de GHZ se implementó en la práctica, utilizando tripletes de fotones entrelazados, en 2000. Para 2002, probar la desigualdad CHSH era factible en cursos de laboratorio de pregrado.

En las pruebas de Bell, puede haber problemas de diseño o configuración experimental que afecten la validez de los hallazgos experimentales. Estos problemas a menudo se denominan "lagunas legales". El propósito del experimento es probar si la naturaleza puede ser descrita por la teoría local de variables ocultas, lo que contradiría las predicciones de la mecánica cuántica.

Las lagunas más frecuentes en los experimentos reales son las lagunas de detección y localidad. La laguna de detección se abre cuando se detecta una pequeña fracción de las partículas (generalmente fotones) en el experimento, lo que hace posible explicar los datos con variables ocultas locales asumiendo que las partículas detectadas son una muestra no representativa. La escapatoria de la localidad se abre cuando las detecciones no se realizan con una separación espacial, haciendo posible que el resultado de una medición influya en la otra sin contradecir la relatividad. En algunos experimentos puede haber defectos adicionales que hacen posibles las explicaciones de variables ocultas locales de las violaciones de la prueba de Bell.

Aunque tanto la laguna de localización como la de detección se habían cerrado en diferentes experimentos, un desafío de larga data era cerrar ambas simultáneamente en el mismo experimento. Esto finalmente se logró en tres experimentos en 2015. Con respecto a estos resultados, Alain Aspect escribe que "... no se puede decir que ningún experimento... esté totalmente libre de lagunas jurídicas" pero dice que los experimentos "eliminan las últimas dudas a las que debemos renunciar" variables ocultas locales, y se refiere a ejemplos de lagunas que quedan como "descabellados" y "ajena a la forma habitual de razonar en física."

Estos esfuerzos para validar experimentalmente las violaciones de las desigualdades de Bell darían como resultado que Clauser, Aspect y Anton Zeilinger obtuvieran el Premio Nobel de Física 2022.

Interpretaciones del teorema de Bell

Las reacciones al teorema de Bell han sido muchas y variadas. Schlosshauer, Kofler y Zeilinger escriben que las desigualdades de Bell brindan "un ejemplo maravilloso de cómo podemos tener un resultado teórico riguroso probado por numerosos experimentos y, sin embargo, estar en desacuerdo sobre las implicaciones".

La Interpretación de Copenhague

La interpretación de Copenhague es una colección de puntos de vista sobre el significado de la mecánica cuántica atribuida principalmente a Niels Bohr y Werner Heisenberg. Es una de las más antiguas de las numerosas interpretaciones propuestas de la mecánica cuántica, ya que sus características datan del desarrollo de la mecánica cuántica durante 1925-1927, y sigue siendo una de las que se enseña con más frecuencia. No existe una declaración histórica definitiva de lo que es la interpretación de Copenhague. En particular, hubo desacuerdos fundamentales entre las opiniones de Bohr y Heisenberg. Algunos principios básicos generalmente aceptados como parte de la colección de Copenhague incluyen la idea de que la mecánica cuántica es intrínsecamente indeterminista, con probabilidades calculadas utilizando la regla de Born, y el principio de complementariedad: ciertas propiedades no pueden definirse conjuntamente para el mismo sistema al mismo tiempo. Para hablar de una propiedad específica de un sistema, ese sistema debe ser considerado dentro del contexto de un arreglo de laboratorio específico. Las cantidades observables correspondientes a arreglos de laboratorio mutuamente excluyentes no se pueden predecir juntas, pero es necesario considerar múltiples experimentos mutuamente excluyentes para caracterizar un sistema. El propio Bohr utilizó la complementariedad para argumentar que la "paradoja" fue falaz. Debido a que las medidas de posición y de momento son complementarias, la elección de medir una excluye la posibilidad de medir la otra. En consecuencia, argumentó, un hecho deducido con respecto a un arreglo de aparato de laboratorio no podía combinarse con un hecho deducido por medio del otro, y por lo tanto, la inferencia de valores predeterminados de posición y momento para la segunda partícula no era válida. Bohr concluyó que los argumentos de EPR 'no justifican su conclusión de que la descripción cuántica resulta ser esencialmente incompleta'.

Las interpretaciones del tipo de Copenhague generalmente toman la violación de las desigualdades de Bell como base para rechazar la suposición a menudo llamada definición contrafáctica o 'realismo', que no es necesariamente lo mismo que abandonar el realismo en un sentido filosófico más amplio. Por ejemplo, Roland Omnès aboga por el rechazo de las variables ocultas y concluye que "la mecánica cuántica es probablemente tan realista como lo será cualquier teoría de su alcance y madurez". Esta es también la ruta que toman las interpretaciones que descienden de la tradición de Copenhague, como las historias consistentes (a menudo anunciadas como 'Copenhague bien hecho'), así como el QBismo.

Interpretación de muchos mundos de la mecánica cuántica

La interpretación de los muchos mundos, también conocida como interpretación de Everett, es local y determinista, ya que consiste en la parte unitaria de la mecánica cuántica sin colapso. Puede generar correlaciones que violen una desigualdad de Bell porque viola una suposición implícita de Bell de que las mediciones tienen un único resultado. De hecho, el teorema de Bell se puede demostrar en el marco de muchos mundos a partir del supuesto de que una medición tiene un único resultado. Por lo tanto, una violación de una desigualdad de Bell puede interpretarse como una demostración de que las medidas tienen múltiples resultados.

La explicación que proporciona para las correlaciones de Bell es que cuando Alice y Bob realizan sus mediciones, se dividen en ramas locales. Desde el punto de vista de cada copia de Alice, hay múltiples copias de Bob experimentando diferentes resultados, por lo que Bob no puede tener un resultado definitivo, y lo mismo ocurre desde el punto de vista de cada copia de Bob. Obtendrán un resultado mutuamente bien definido solo cuando sus futuros conos de luz se superpongan. En este punto podemos decir que la correlación de Bell comienza a existir, pero fue producida por un mecanismo puramente local. Por tanto, la violación de una desigualdad de Bell no puede interpretarse como una prueba de no localidad.

Variables ocultas no locales

La mayoría de los defensores de la idea de las variables ocultas creen que los experimentos han descartado las variables ocultas locales. Están dispuestos a renunciar a la localidad, explicando la violación de la desigualdad de Bell mediante una teoría de la variable oculta no local, en la que las partículas intercambian información sobre sus estados. Esta es la base de la interpretación de Bohm de la mecánica cuántica, que requiere que todas las partículas del universo puedan intercambiar información instantáneamente con todas las demás. Un desafío para las teorías de variables ocultas no locales es explicar por qué esta comunicación instantánea puede existir al nivel de las variables ocultas, pero no puede usarse para enviar señales. Un experimento de 2007 descartó una gran clase de teorías de variables ocultas no locales no bohmianas, aunque no la mecánica bohmiana en sí.

La interpretación transaccional, que postula que las ondas viajan tanto hacia atrás como hacia adelante en el tiempo, tampoco es local.

Superdeterminismo

Una suposición necesaria para derivar el teorema de Bell es que las variables ocultas no están correlacionadas con la configuración de medición. Esta suposición se ha justificado sobre la base de que el experimentador tiene "libre albedrío" elegir los escenarios, y que es necesario hacer ciencia en primer lugar. Una teoría (hipotética) en la que la elección de la medida está necesariamente correlacionada con el sistema que se mide se conoce como superdeterminista.

Algunos defensores de los modelos deterministas no han renunciado a las variables ocultas locales. Por ejemplo, Gerard 't Hooft ha argumentado que el superdeterminismo no puede descartarse.