Tensegridad

La estructura de tensión más simple (un precio T3). Cada uno de los tres miembros de compresión (verde) es simétrico con los otros dos, y simétrico de extremo a extremo. Cada extremo está conectado a tres cables (rojo), que proporcionan tensión y definen precisamente la posición de ese extremo de la misma manera que los tres cables del Skylon definen el extremo inferior de su pilar cónico.

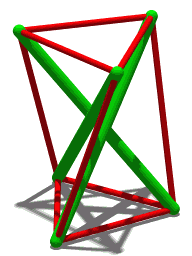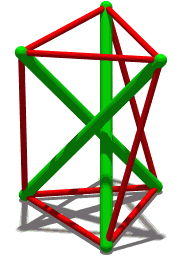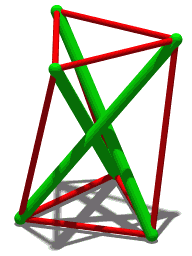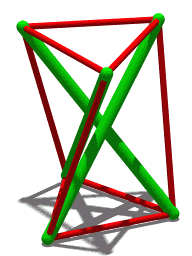
Tensegridad, integridad tensional o compresión flotante es un principio estructural basado en un sistema de componentes aislados bajo compresión dentro de una red de tensión continua, y dispuestos de tal manera que los elementos comprimidos (normalmente barras o puntales) no se toquen entre sí mientras que los elementos pretensados y tensados (normalmente cables o tendones) delimitan espacialmente el sistema.

If historically the boxing event was bare-fisted, now practicing the sport in a regulated manner dictates the use of gloves, which provide a degree of cushioning.

Glove manufacturing has evolved, and sometimes the materials used have changed. Cow or goat skin has been used for the making, and straw or horse hair has been used for padding. Synthetic materials are commonly used. The materials used affect the toughness or protection of the gloves.

One of the purposes of gloves is to protect the knuckles. Regular boxing gloves look like a pair of puffy gloves, and are tied around the wrists on the inside of the forearm. There are gloves that instead of having laces have velcro.

• miembros cargados en compresión pura o tensión pura, lo que significa que la estructura sólo fallará si los cables se rinden o las varillas se hebillan. Esto permite optimizar las propiedades materiales y la geometría transversal de cada miembro a la carga particular que lleva.
• precarga o prestreza tensional permite que los cables estén siempre en tensión, para mantener la integridad estructural.
• estabilidad mecánica, que permite a los miembros permanecer en tensión/compresión a medida que aumenta el estrés sobre la estructura. La estructura también se vuelve más rígida a medida que aumenta la tensión del cable.

Debido a estos patrones, ningún miembro estructural experimenta un momento de flexión y no hay esfuerzos cortantes dentro del sistema. Esto puede producir estructuras excepcionalmente fuertes y rígidas por su masa y por la sección transversal de los componentes. La carga de al menos algunas estructuras de tensegridad provoca una respuesta auxética y una relación de Poisson negativa, p. el prisma T3 y el icosaedro de tensegridad de 6 puntales.

El Skylon en el Festival de Gran Bretaña, 1951

Un bloque de construcción conceptual de la tensegridad se ve en el Skylon de 1951. Seis cables, tres en cada extremo, sujetan la torre en posición. Los tres cables conectados a la parte inferior "definen" su localización. Los otros tres cables simplemente lo mantienen vertical.

Una estructura de tensegridad de tres barras (que se muestra a la derecha) se basa en esta estructura más simple: los extremos de cada barra verde se parecen a la parte superior e inferior del Skylon. Siempre que el ángulo entre dos cables cualesquiera sea inferior a 180°, la posición de la varilla está bien definida. Si bien tres cables son el mínimo requerido para la estabilidad, se pueden conectar cables adicionales a cada nodo por motivos estéticos o para aumentar la estabilidad. Por ejemplo, la torre de agujas de Snelson usa un patrón repetido construido usando nodos que están conectados a 5 cables cada uno.

Eleanor Heartney destaca la transparencia visual como una cualidad estética importante de estas estructuras. Korkmaz et al. ha argumentado que las estructuras ligeras de tensegridad son adecuadas para la arquitectura adaptativa.

Aplicaciones

Las tensegridades vieron una mayor aplicación en la arquitectura a partir de la década de 1960, cuando Maciej Gintowt y Maciej Krasiński diseñaron el complejo de arena Spodek (en Katowice, Polonia), como una de las primeras estructuras importantes en emplear el principio de la tensegridad. El techo utiliza una superficie inclinada controlada por un sistema de cables que sostienen su circunferencia. Los principios de tensegridad también se utilizaron en el Estadio de Gimnasia Olímpica de Seúl de David Geiger (para los Juegos Olímpicos de verano de 1988) y en el Georgia Dome (para los Juegos Olímpicos de verano de 1996). Tropicana Field, sede del equipo de béisbol de las ligas mayores Tampa Bay Rays, también tiene un techo de cúpula sostenido por una gran estructura de tensegridad.

Puente de tensión más grande del mundo, Puente Kurilpa – Brisbane

El 4 de octubre de 2009, se inauguró el puente Kurilpa sobre el río Brisbane en Queensland, Australia. Una estructura atirantada de mástiles múltiples basada en los principios de tensegridad, actualmente es el puente de tensegridad más grande del mundo.

Super Ball de la NASA Bot es un prototipo temprano para aterrizar en otro planeta sin una bolsa de aire, y luego ser móvil para explorar. La estructura de tensegridad proporciona el cumplimiento estructural absorbiendo fuerzas de impacto de aterrizaje y movimiento se aplica cambiando longitudes de cable, 2014.

Desde principios de la década de 2000, las tensegridades también han atraído el interés de los expertos en robótica debido a su potencial para diseñar robots ligeros y resistentes. Numerosas investigaciones han investigado rovers de tensegridad, robots bio-imitadores y robots blandos modulares. El robot de tensegridad más famoso es el Super Ball Bot, un rover para la exploración espacial que utiliza una estructura de tensegridad de 6 barras, actualmente en desarrollo en NASA Ames.

Biología

La biotensegridad, un término acuñado por el Dr. Stephen Levin, es una aplicación teórica extendida de los principios de la tensegridad a las estructuras biológicas. Las estructuras biológicas como músculos, huesos, fascias, ligamentos y tendones, o membranas celulares rígidas y elásticas, se fortalecen por el unísono de partes tensadas y comprimidas. El sistema musculoesquelético consiste en una red continua de músculos y tejidos conectivos, mientras que los huesos brindan soporte compresivo discontinuo, mientras que el sistema nervioso mantiene la tensión in vivo a través de estímulos eléctricos. Levin afirma que la columna vertebral humana también es una estructura de tensegridad, aunque no hay apoyo para esta teoría desde una perspectiva estructural.

Donald E. Ingber ha desarrollado una teoría de la tensegridad para describir numerosos fenómenos observados en biología molecular. Por ejemplo, las formas expresadas de las células, ya sean sus reacciones a la presión aplicada, las interacciones con los sustratos, etc., pueden modelarse matemáticamente representando el citoesqueleto de la célula como una tensegridad. Además, los patrones geométricos que se encuentran en toda la naturaleza (la hélice del ADN, la cúpula geodésica de un volvox, el Buckminsterfullereno y más) también pueden entenderse aplicando los principios de la tensegridad al autoensamblaje espontáneo de compuestos, proteínas e incluso órganos.. Este punto de vista está respaldado por cómo las interacciones de tensión-compresión de la tensegridad minimizan el material necesario para mantener la estabilidad y lograr la resiliencia estructural, aunque la comparación con materiales inertes dentro de un marco biológico no tiene una premisa ampliamente aceptada dentro de la ciencia fisiológica. Por lo tanto, las presiones de la selección natural probablemente favorecerían los sistemas biológicos organizados en forma de tensegridad.

Como explica Ingber:

Los miembros portadores de tensión en estas estructuras – ya sean las cúpulas de Fuller o las esculturas de Snelson – mapean los caminos más cortos entre los miembros adyacentes (y por lo tanto, por definición, están ordenados geodésicamente). Las fuerzas de tensión se transmiten naturalmente a lo largo de la distancia más corta entre dos puntos, por lo que los miembros de una estructura de tensión están precisamente posicionados para soportar mejor el estrés. Por esta razón, las estructuras de tensión ofrecen una cantidad máxima de fuerza.

En embriología, Richard Gordon propuso que las ondas de diferenciación embrionaria se propagan mediante un 'orgánulo de diferenciación' donde el citoesqueleto se ensambla en una estructura de tensegridad biestable en el extremo apical de las células llamado "divisor de estado celular".

Orígenes e historia del arte

Diseño X-Module de Kenneth Snelson en 1948 encarnado en una columna de dos módulos

Los orígenes de la tensegridad son controvertidos. Muchas estructuras tradicionales, como los kayaks de piel sobre bastidor y los shōji, utilizan elementos de tensión y compresión de manera similar.

El artista ruso Viatcheslav Koleichuk afirmó que la idea de la tensegridad fue inventada primero por Kārlis Johansons (en ruso como alemán como Karl Ioganson) (lv), un artista de vanguardia soviético de ascendencia letona, quien contribuyó con algunas obras a la exposición principal. del constructivismo ruso en 1921. La afirmación de Koleichuk fue respaldada por Maria Gough para una de las obras de la exposición constructivista de 1921. Snelson ha reconocido a los constructivistas como una influencia para su trabajo (¿consulta?). El ingeniero francés David Georges Emmerich también ha notado cómo el trabajo de Kārlis Johansons (y las ideas de diseño industrial) parecían prever conceptos de tensegridad.

En 1948, el artista Kenneth Snelson produjo su innovador "X-Piece" después de exploraciones artísticas en Black Mountain College (donde Buckminster Fuller daba conferencias) y en otros lugares. Algunos años más tarde, el término "tensegridad" fue acuñado por Fuller, mejor conocido por sus cúpulas geodésicas. A lo largo de su carrera, Fuller había experimentado con la incorporación de componentes de tracción en su trabajo, como en la estructura de sus casas Dymaxion.

La innovación de Snelson en 1948 impulsó a Fuller a encargar de inmediato un mástil de Snelson. En 1949, Fuller desarrolló un icosaedro de tensegridad basado en la tecnología, y él y sus alumnos desarrollaron rápidamente otras estructuras y aplicaron la tecnología para construir cúpulas. Después de una pausa, Snelson también produjo una gran cantidad de esculturas basadas en conceptos de tensegridad. Su cuerpo principal de trabajo comenzó en 1959 cuando tuvo lugar una exposición fundamental en el Museo de Arte Moderno. En la exhibición del MOMA, Fuller había mostrado el mástil y algunos de sus otros trabajos. En esta exhibición, Snelson, luego de una discusión con Fuller y los organizadores de la exhibición sobre el crédito por el mástil, también mostró algunas obras en una vitrina.

La pieza más conocida de Snelson es su Torre de aguja de 18 metros de altura de 1968.

Estabilidad

Prismas de tensegridad

La estructura de tensegridad de tres varillas (prisma de 3 vías) tiene la propiedad de que, para una longitud dada (común) de "barra" de miembro de compresión (hay tres en total) y una longitud dada (común) de cable de tensión " tendón” (seis en total) que conecta los extremos de las varillas entre sí, hay un valor particular para la longitud (común) del tendón que conecta las puntas de las varillas con las bases de las varillas vecinas que hace que la estructura mantenga una forma estable. Para una estructura de este tipo, es sencillo demostrar que el triángulo formado por las partes superiores de las barras y el formado por las partes inferiores de las barras giran entre sí en un ángulo de 5π/6 (radianes).

Sultan, et al. analizan la estabilidad ("pretensabilidad") de varias estructuras de tensegridad de dos etapas.

El prisma T3 (también conocido como Triplex) se puede obtener a través de la búsqueda de la forma de un prisma triangular recto. Su estado de autoequilibrio se da cuando los triángulos base se encuentran en planos paralelos separados por un ángulo de giro de π/6. La fórmula para su estado único de autoesfuerzo está dada por,

$${displaystyle omega =omega [{1} [-{sqrt {}}3),-{sqrt {}3),-{sqrt {}3),{sqrt {}}3),{sqrt {}3),{sqrt {}3),{sqrt { {}}}3,1,1,1,1,1,1,1,1} {}}}} {}} {}} {}}}}} {}}}}}}}} {}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}} {}}}}}}}} {}}}}}}}}}} {} {\}}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$$

Aquí, los tres primeros valores negativos corresponden a los componentes internos en compresión, mientras que el resto corresponde a los cables en tracción.

Icosaedros de tensegridad

Modelo matemático de la tensión icosahedron

Diferentes formas de tensión icosahedra, dependiendo de la relación entre las longitudes de los tendones y las tribus.

Una tensa icosahedro hecha de pajas y cuerdas

La tensa icosahedron, primero estudiada por Snelson en 1949, tiene struts y tendones a lo largo de los bordes de un poliedro llamado icosahedro de Jessen. Es una construcción estable, aunque con movilidad infinitesimal. Para ver esto, considere un cubo de longitud lateral 2d, centrado en el origen. Coloque una punta de longitud 2l en el plano de cada cara de cubo, tal que cada punta es paralela a un borde de la cara y se centra en la cara. Además, cada strut debe ser paralelo a la strut en la cara opuesta del cubo, pero ortogonal a todos los demás struts. Si las coordenadas cartesianas de una tribu son ${displaystyle (0,d,l)}$ y ${displaystyle (0,d,-l)}$, los de su strut paralelo serán, respectivamente, ${displaystyle (0,-d,-l)}$ y ${displaystyle (0,-d,l)}$. Las coordenadas de los otros extremos de strut se obtienen permutando las coordenadas, por ejemplo, ${displaystyle (0,d,l)rightarrow (d,l,0)rightarrow (l,0,d)}$ (simetría rotacional en la diagonal principal del cubo).

La distancia s entre dos vértices vecinos (0, d, l) y (d, l, 0) es

$${displaystyle s^{2}=(d-l)}{2}+d^{2}+l^{2}=2left(d-{frac {1}{2}},lright)^{2}+{2}{2}},l^{2}}}}}}}}}}}}}}} {$$

Imagínese esta figura construida a partir de struts de longitud dada 2l y tendones (conectando vértices vecinos) de longitud dada s, con ${fnMicroc} {3}{2},l}$. La relación nos dice que hay dos valores posibles para d: uno realizado al empujar los struts juntos, el otro al tirarlos separados. En el caso particular ${displaystyle s={sqrt {frac {3}{2},l}$ los dos extremos coinciden, y ${displaystyle d={frac} {c},l}$, por lo tanto la figura es la tensión estable icosahedron. Esta elección de parámetros da a los vértices las posiciones del icosahedro de Jessen; son diferentes del icosahedro regular, por el cual la relación de ${displaystyle d}$ y ${displaystyle l}$ sería la relación de oro, en lugar de 2. Sin embargo, ambos conjuntos de coordenadas se encuentran a lo largo de una familia continua de posiciones que van desde el cuboctaedro hasta el octaedro (como casos límite), que están vinculados por una transformación helicoidal contractiva/expansiva. Esta cinemática del cuboctaedro es la geometría del movimiento de la tensegridad icosahedron. Fue descrito por primera vez por H. S. M. Coxeter y luego llamado la "transformación de jitterbug" por Buckminster Fuller.

Dado que el icosaedro de tensegridad representa un punto extremo de la relación anterior, tiene una movilidad infinitesimal: un pequeño cambio en la longitud s del tendón (por ejemplo, al estirar los tendones) da como resultado una mucho mayor cambio de la distancia 2d de los puntales.

Patentes

• U.S. Patent 3,063,521"Estructuras de tensión-integridad", 13 de noviembre de 1962, Buckminster Fuller.
• Patente francés No. 1,377,290, "Construcción de Reseaux Autotendants", 28 de septiembre de 1964, David Georges Emmerich.
• Patente francés No. 1,377,291, "Structures Linéaires Autotendants", 28 de septiembre de 1964, David Georges Emmerich.
• U.S. Patente 3,139,957, "Edificio de Suspensión" (también llamado aspensión), 7 de julio de 1964, Buckminster Fuller.
• U.S. Patent 3,169,611, "Continuous Tension, Discontinuous Compression Structure", 16 de febrero de 1965, Kenneth Snelson.
• U.S. Patente 3,866,366, "No-symmetrical Tension-Integrity Structures", 18 de febrero de 1975, Buckminster Fuller.

Estructuras básicas de tensegridad

• 

  La estructura de tensión más simple, un 3-prisma

• 

  Otro 3-prisma

• 

  Una estructura similar pero con cuatro miembros de compresión

• 

  Proto-Tensegrity Prism de Karl Ioganson, 1921

• 

  Tensegrity Icosahedron, Buckminster Fuller, 1949

• 

  Tensegrity Tetrahedron, Francesco della Salla, 1952

• 

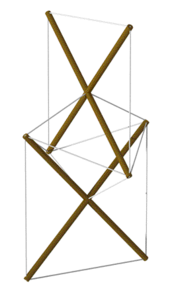
  Tensegrity X-Module Tetrahedron, Kenneth Snelson, 1959

Estructuras de tensegridad

• 

  La aguja de Kenneth Snelson Escultura de arte torre.

• 

  Una cúpula tenscura hecha de estacas de jardín y gemela de nylon construida en el patio de una casa, 2009

• 

  Una estructura de tensión alta de 12m exhibe en la Ciudad de la Ciencia, Kolkata.

• 

  Disipate, una escultura de arte de torre de reloj de arena, incluyendo la estructura de tensión, construida en AfrikaBurn, 2015, un evento regional de Hombre Ardiente