Temperatura termodinámica
La temperatura termodinámica es una cantidad definida en la termodinámica a diferencia de la teoría cinética o la mecánica estadística.
Históricamente, la temperatura termodinámica fue definida por Kelvin en términos de una relación macroscópica entre el trabajo termodinámico y la transferencia de calor como se define en la termodinámica, pero el kelvin fue redefinido por un acuerdo internacional en 2019 en términos de fenómenos que ahora se entienden como manifestaciones de la energía cinética del movimiento libre de partículas microscópicas como átomos, moléculas y electrones. Desde el punto de vista termodinámico, por razones históricas, por cómo se define y se mide, esta definición cinética microscópica se considera como una definición "empírica" la temperatura. Se adoptó porque en la práctica generalmente se puede medir con mayor precisión que la temperatura termodinámica de Kelvin.
Una lectura de temperatura termodinámica de cero es de particular importancia para la tercera ley de la termodinámica. Por convención, se expresa en la escala Kelvin de temperatura en la que la unidad de medida es el kelvin (símbolo de unidad: K). A modo de comparación, una temperatura de 295 K es igual a 21,85 °C y 71,33 °F.
Resumen
La temperatura termodinámica, a diferencia de la temperatura SI, se define en términos de un ciclo de Carnot macroscópico. La temperatura termodinámica es importante en termodinámica porque se define en términos puramente termodinámicos. La temperatura SI es conceptualmente muy diferente de la temperatura termodinámica. La temperatura termodinámica se definió rigurosamente históricamente mucho antes de que existiera un conocimiento justo de partículas microscópicas como átomos, moléculas y electrones.
El Sistema Internacional de Unidades (SI) especifica la escala absoluta internacional para medir la temperatura y la unidad de medida kelvin (símbolo de unidad: K) para valores específicos a lo largo de la escala. El kelvin también se usa para indicar intervalos de temperatura (un intervalo o diferencia entre dos temperaturas) según el siguiente ejemplo de uso: "Una soldadura de estaño/plomo 60/40 no es eutéctica y es plástico a través de un rango de 5 kelvins a medida que se solidifica." Un intervalo de temperatura de un grado Celsius tiene la misma magnitud que un kelvin.
La magnitud del kelvin se redefinió en 2019 en relación con la propiedad muy física subyacente a la temperatura termodinámica: la energía cinética del movimiento de partículas libres atómicas. La redefinición fijó la constante de Boltzmann precisamente en 1,380649×10−23 julios por kelvin (J/K). La unidad de medida compuesta para la constante de Boltzmann a menudo también se escribe como J·K−1, con un punto de multiplicación (·) y un símbolo de kelvin seguido de un exponente negativo 1 en superíndice. Esta es otra sintaxis matemática que denota la misma medida: julios (la unidad SI para energía, incluida la energía cinética) por kelvin.
La propiedad microscópica que confiere temperatura a las sustancias materiales se puede entender fácilmente examinando la ley de los gases ideales, que relaciona, según la constante de Boltzmann, cómo la energía térmica provoca cambios definidos con precisión en la presión y la temperatura de ciertos gases. Esto se debe a que los gases monoatómicos como el helio y el argón se comportan cinéticamente como bolas de billar esféricas y perfectamente elásticas que se mueven libremente y que se mueven solo en un subconjunto específico de los posibles movimientos que pueden ocurrir en la materia: el que comprende los tres grados de traslación. de libertad. Los grados de libertad de traslación son los movimientos familiares similares a una bola de billar a lo largo de los ejes X, Y y Z del espacio 3D (consulte la Fig. 1, a continuación). Esta es la razón por la cual todos los gases nobles tienen la misma capacidad calorífica específica por átomo y por qué ese valor es el más bajo de todos los gases.
Las moléculas (dos o más átomos unidos químicamente), sin embargo, tienen una estructura interna y, por lo tanto, tienen grados de libertad internos adicionales (consulte la Fig. 3, a continuación), que hace que las moléculas absorban más energía térmica para cualquier cantidad dada de aumento de temperatura que los gases monoatómicos. La energía térmica nace en todos los grados de libertad disponibles; esto está de acuerdo con el teorema de equipartición, por lo que todos los grados de libertad internos disponibles tienen la misma temperatura que sus tres grados de libertad externos. Sin embargo, la propiedad que da a todos los gases su presión, que es la fuerza neta por unidad de área sobre un recipiente que surge de las partículas de gas que retroceden, es una función de la energía cinética soportada en los tres grados de traslación de los átomos y moléculas que se mueven libremente. de libertad.
Fijar la constante de Boltzmann en un valor específico, junto con otras reglas, tuvo el efecto de establecer con precisión la magnitud del intervalo unitario de temperatura SI, el kelvin, en términos del comportamiento cinético promedio de los gases nobles. Además, el punto de partida de la escala de temperatura termodinámica, el cero absoluto, se reafirmó como el punto en el que la energía cinética media cero permanece en una muestra; el único movimiento de partículas restante es el que comprende vibraciones aleatorias debidas a la energía de punto cero.
Cero absoluto de temperatura
Las escalas de temperatura son numéricas. El cero numérico de una escala de temperatura no está ligado al cero absoluto de temperatura. Sin embargo, algunas escalas de temperatura tienen su cero numérico coincidente con el cero absoluto de temperatura. Algunos ejemplos son la escala de temperatura del SI internacional, la escala de temperatura de Rankine y la escala de temperatura termodinámica. Otras escalas de temperatura tienen su cero numérico lejos del cero absoluto de temperatura. Ejemplos son la escala Fahrenheit y la escala Celsius.
En el punto cero de la temperatura termodinámica, el cero absoluto, las partículas constituyentes de la materia tienen un movimiento mínimo y no pueden volverse más frías. El cero absoluto, que es una temperatura de cero kelvins (0 K), es exactamente igual a −273,15 °C y −459,67 °F. La materia en el cero absoluto no tiene energía cinética promedio transferible restante y el único movimiento de partículas restante se debe a un fenómeno mecánico cuántico omnipresente llamado ZPE (Zero-Point Energy). Aunque los átomos en, por ejemplo, un contenedor de helio líquido que estaba precisamente en el cero absoluto todavía se empujarían ligeramente debido a la energía del punto cero, una máquina térmica teóricamente perfecta con tal helio como uno de sus componentes de trabajo los fluidos nunca podrían transferir ninguna energía cinética neta (energía térmica) al otro fluido de trabajo y no podría ocurrir ningún trabajo termodinámico.
La temperatura generalmente se expresa en términos absolutos cuando se examinan científicamente las interrelaciones de la temperatura con otras propiedades físicas de la materia, como su volumen o presión (consulte la ley de Gay-Lussac), o la longitud de onda de su emisión. radiación de cuerpo negro. La temperatura absoluta también es útil cuando se calculan las velocidades de reacción química (consulte la ecuación de Arrhenius). Además, la temperatura absoluta se usa típicamente en criogenia y fenómenos relacionados como la superconductividad, según el siguiente ejemplo de uso: "Convenientemente, la temperatura de transición del tantalio (Tc) de 4,4924 kelvin está ligeramente por encima del punto de ebullición de 4,2221 K del helio."
Constante de Boltzmann
La constante de Boltzmann y sus fórmulas relacionadas describen el ámbito de la cinética de partículas y los vectores de velocidad, mientras que ZPE (energía de punto cero) es un campo de energía que empuja a las partículas de formas descritas por las matemáticas de la mecánica cuántica. En colisiones atómicas y moleculares en gases, ZPE introduce un grado de caos, es decir, imprevisibilidad, a la cinética de rebote; es tan probable que haya menos movimiento de partículas inducido por ZPE después de una colisión determinada como más. Esta naturaleza aleatoria de ZPE es la razón por la que no tiene un efecto neto sobre la presión o el volumen de cualquier cantidad a granel (una cantidad estadísticamente significativa de partículas) de gases. Sin embargo, en temperatura T = 0 materia condensada; por ejemplo, sólidos y líquidos, ZPE provoca empujones interatómicos donde los átomos estarían perfectamente estacionarios. Dado que los efectos del mundo real que ZPE tiene sobre las sustancias pueden variar a medida que se altera un sistema termodinámico (por ejemplo, debido a ZPE, el helio no se congelará a menos que esté bajo una presión de al menos 2,5 MPa (25 bar)), ZPE es en gran medida una forma de energía térmica y puede incluirse correctamente al contar la energía interna de una sustancia.
Escala Rankine
Aunque ha habido muchas otras escalas de temperatura a lo largo de la historia, solo ha habido dos escalas para medir la temperatura termodinámica donde el cero absoluto es su punto nulo (0): la escala Kelvin y la escala Rankine.
En todo el mundo científico donde las mediciones modernas casi siempre se realizan utilizando el Sistema Internacional de Unidades, la temperatura termodinámica se mide utilizando la escala Kelvin. La escala Rankine es parte de las unidades de ingeniería inglesas en los Estados Unidos y encuentra uso en ciertos campos de ingeniería, particularmente en obras de referencia heredadas. La escala Rankine utiliza el grado Rankine (símbolo: °R) como unidad, que tiene la misma magnitud que el grado Fahrenheit (símbolo: °F).
Un incremento unitario de un grado Rankine es precisamente 1,8 veces menor en magnitud que un kelvin; por lo tanto, para convertir una temperatura específica en la escala Kelvin a la escala Rankine, K × 1.8 = °R, y para convertir una temperatura en la escala Rankine a la escala Kelvin, °R / 1.8 = K. En consecuencia, el cero absoluto es "0" para ambas escalas, pero el punto de fusión del hielo de agua (0 °C y 273,15 K) es 491,67 °R.
Para convertir intervalos de temperatura (un lapso o diferencia entre dos temperaturas), se utilizan las mismas fórmulas del párrafo anterior; por ejemplo, un rango de 5 kelvin es exactamente igual a un rango de 9 grados Rankine.
Redefinición moderna de la kelvin
(feminine)Durante 65 años, entre 1954 y la redefinición de las unidades básicas del SI en 2019, un intervalo de temperatura de un kelvin se definió como 1/273,16 la diferencia entre el punto triple del agua y el cero absoluto. La resolución de 1954 de la Oficina Internacional de Pesas y Medidas (conocida por el acrónimo en francés BIPM), además de resoluciones y publicaciones posteriores, definió el punto triple del agua como exactamente 273,16 K y reconoció que era una "práctica común" 34; aceptar que debido a convenciones previas (a saber, que 0 °C se había definido durante mucho tiempo como el punto de fusión del agua y que se había determinado experimentalmente que el punto triple del agua era indistinguiblemente cercano a 0,01 °C), la diferencia entre el La escala Celsius y la escala Kelvin se aceptan como 273,15 kelvin; es decir, 0 °C equivale a 273,15 kelvin. El efecto neto de esta y otras resoluciones posteriores fue doble: 1) definieron el cero absoluto exactamente como 0 K, y 2) definieron que el punto triple del agua especial controlada isotópicamente llamada Vienna Standard Mean Ocean Water era precisamente 273,16 K y 0,01 ºC Un efecto de las resoluciones antes mencionadas fue que el punto de fusión del agua, aunque muy cercano a 273,15 K y 0 °C, no era un valor definitorio y estaba sujeto a refinamiento con mediciones más precisas.
El estándar BIPM de 1954 hizo un buen trabajo al establecer, dentro de las incertidumbres debidas a las variaciones isotópicas entre las muestras de agua, las temperaturas alrededor de los puntos triple y de congelación del agua, pero requería que valores intermedios entre el triple punto y cero absoluto, así como valores extrapolados de temperatura ambiente y más allá, que se determinarán experimentalmente a través de aparatos y procedimientos en laboratorios individuales. Esta deficiencia fue abordada por la Escala Internacional de Temperatura de 1990, o ITS‑90, que definió 13 puntos adicionales, de 13,8033 K a 1357,77 K. Si bien la definición, ITS‑90 tuvo, y todavía tiene, algunos desafíos, en parte porque ocho de sus valores extrapolados dependen de los puntos de fusión o congelación de las muestras de metal, que deben permanecer extremadamente puros para que sus puntos de fusión o congelación no se vean afectados, generalmente deprimidos.
La redefinición de 2019 de las unidades básicas del SI tuvo como objetivo principal desvincular gran parte de los fundamentos de definición del sistema SI del kilogramo, que era el último artefacto físico que definía una unidad básica del SI (un cilindro de platino/iridio almacenados bajo tres campanas de cristal anidadas en una caja fuerte ubicada en Francia) y que tenían una estabilidad muy cuestionable. La solución requería que cuatro constantes físicas, incluida la constante de Boltzmann, fueran fijadas por definición.
Asignar a la constante de Boltzmann un valor definido con precisión no tuvo ningún efecto práctico en la termometría moderna, excepto en las mediciones más exquisitamente precisas. Antes de la redefinición, el punto triple del agua era exactamente 273,16 K y 0,01 °C y se determinó experimentalmente que la constante de Boltzmann era 1,38064903(51)×10−23 J/K, donde el "(51)" denota la incertidumbre en los dos dígitos menos significativos (el 03) y equivale a una incertidumbre estándar relativa de 0,37 ppm. Luego, definiendo la constante de Boltzmann exactamente como 1.380649 ×10−23 J/K, el 0,37 La incertidumbre de ppm se transfirió al punto triple del agua, que se convirtió en un valor determinado experimentalmente de 273,1600±0.0001 K (0.0100±0.0001 °C). Que el punto triple del agua terminara muy cerca de 273,16 K después de la redefinición del SI no fue un accidente; el valor final de la constante de Boltzmann se determinó, en parte, a través de ingeniosos experimentos con argón y helio que utilizaron el punto triple del agua como temperatura de referencia clave.
A pesar de la redefinición de 2019, las celdas de punto triple de agua continúan sirviendo en la termometría moderna como referencias de calibración sumamente precisas a 273,16 K y 0,01 °C. Además, el punto triple del agua sigue siendo uno de los 14 puntos de calibración que comprende el ITS‑90, que abarca desde el punto triple del hidrógeno (13,8033 K) hasta el punto de congelación del cobre (1357,77 K), que es un rango termodinámico casi cien veces mayor. la temperatura.
Relación de temperatura, movimientos, conducción y energía térmica

Naturaleza de la energía cinética, movimiento de traslación y temperatura
La temperatura termodinámica de cualquier cantidad a granel de una sustancia (una cantidad estadísticamente significativa de partículas) es directamente proporcional a la energía cinética promedio promedio de un tipo específico de movimiento de partículas conocido como translacional movimiento. Estos movimientos simples en las tres dimensiones del espacio de los ejes X, Y y Z significan que las partículas se mueven en los tres grados de libertad espaciales. Esta forma particular de energía cinética a veces se denomina temperatura cinética. El movimiento de traslación es solo una forma de energía térmica y es lo que le da a los gases no solo su temperatura, sino también su presión y la gran mayoría de su volumen. Esta relación entre la temperatura, la presión y el volumen de los gases se establece mediante la fórmula de la ley de los gases ideales pV = nRT y está incorporado en las leyes de los gases.
Aunque la energía cinética transmitida exclusivamente en los tres grados de libertad de traslación comprende la temperatura termodinámica de una sustancia, las moléculas, como se puede ver en la Fig. 3, pueden tener otros grados de libertad, todos los cuales pertenecen a tres categorías: longitud de enlace, ángulo de enlace y rotación. Las tres categorías adicionales no están necesariamente disponibles para todas las moléculas, e incluso para las moléculas que pueden experimentar las tres, algunas pueden "congelarse" por debajo de cierta temperatura. No obstante, todos esos grados de libertad que están disponibles para las moléculas bajo un conjunto particular de condiciones contribuyen a la capacidad calorífica específica de una sustancia; es decir, aumentan la cantidad de calor (energía cinética) necesaria para elevar una determinada cantidad de sustancia en un kelvin o un grado Celsius.
La relación entre energía cinética, masa y velocidad viene dada por la fórmula Ek = 1/2mv2. En consecuencia, las partículas con una unidad de masa que se mueve a una unidad de velocidad tienen exactamente la misma energía cinética y exactamente la misma temperatura que aquellas con cuatro veces la masa pero la mitad de la velocidad.
La medida en que la energía cinética del movimiento de traslación en un conjunto estadísticamente significativo de átomos o moléculas en un gas contribuye a la presión y el volumen de ese gas es una función proporcional de la temperatura termodinámica establecida por la constante de Boltzmann (símbolo: kB). La constante de Boltzmann también relaciona la temperatura termodinámica de un gas con la energía cinética media del movimiento de traslación de una partícula individual de la siguiente manera:
- E~ ~ {displaystyle {fnMicrosoft}} es la energía cinética media para una partícula individual
- kB = 1.380649×10,23 a 23J/K
- T es la temperatura termodinámica de la cantidad de vracs de la sustancia
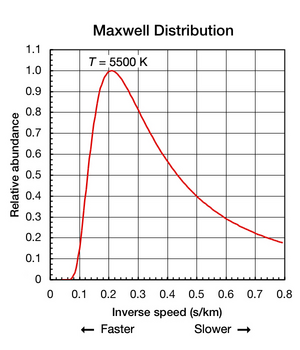
Si bien la constante de Boltzmann es útil para encontrar la energía cinética media en una muestra de partículas, es importante tener en cuenta que incluso cuando una sustancia está aislada y en equilibrio termodinámico (todas las partes están a una temperatura uniforme y no hay calor). dentro o fuera de él), los movimientos de traslación de átomos y moléculas individuales ocurren en una amplia gama de velocidades (ver animación en Fig. 1 arriba). En cualquier instante, la proporción de partículas que se mueven a una velocidad dada dentro de este rango está determinada por la probabilidad descrita por la distribución de Maxwell-Boltzmann. El gráfico que se muestra aquí en Fig. 2 muestra la distribución de velocidad de los átomos de helio de 5500 K. Tienen una velocidad más probable de 4,780 km/s (0,2092 s/km). Sin embargo, cierta proporción de átomos en un instante dado se mueve más rápido mientras que otros se mueven relativamente lento; algunos están momentáneamente en un punto muerto virtual (fuera del eje x a la derecha). Este gráfico usa velocidad inversa para su eje x, de modo que la forma de la curva se puede comparar fácilmente con las curvas en la Fig. 5 a continuación. En ambos gráficos, el cero en el eje x representa una temperatura infinita. Además, los ejes x e y en ambos gráficos están escalados proporcionalmente.
Altas velocidades de movimiento de traslación
Aunque se requiere un equipo de laboratorio muy especializado para detectar directamente los movimientos de traslación, las colisiones resultantes de átomos o moléculas con pequeñas partículas suspendidas en un fluido producen un movimiento browniano que se puede ver con un microscopio ordinario. Los movimientos de traslación de las partículas elementales son muy rápidos y se requieren temperaturas cercanas al cero absoluto para observarlos directamente. Por ejemplo, cuando los científicos del NIST lograron una temperatura fría récord de 700 nK (mil millonésimas de kelvin) en 1994, utilizaron equipos láser de red óptica para enfriar adiabáticamente los átomos de cesio. Luego apagaron los láseres de atrapamiento y midieron directamente velocidades atómicas de 7 mm por segundo para calcular su temperatura. Las fórmulas para calcular la velocidad y la velocidad del movimiento de traslación se dan en la siguiente nota al pie.

No es difícil imaginar movimientos atómicos debidos a la temperatura cinética, ni distinguir entre tales movimientos y los debidos a la energía de punto cero. Considere el siguiente experimento mental hipotético, como se ilustra en Fig. 2,5 a la izquierda, con un átomo que está muy cerca del cero absoluto. Imagínese mirando a través de un microscopio óptico común ajustado a 400 de potencia, que es aproximadamente el aumento práctico máximo para los microscopios ópticos. Dichos microscopios generalmente brindan campos de visión de un poco más de 0,4 mm de diámetro. En el centro del campo de visión hay un solo átomo de argón levitado (el argón comprende aproximadamente el 0,93% del aire) que está iluminado y brillando contra un fondo oscuro. Si este átomo de argón estuviera a una una trillonésima de un kelvin por encima del cero absoluto, más allá del récord, y se moviera perpendicularmente al campo de visión hacia la derecha, necesitaría 13,9 segundos para moverse de el centro de la imagen hasta la marca de verificación de 200 micras; esta distancia de viaje es aproximadamente la misma que el ancho del punto al final de esta oración en los monitores de computadora modernos. A medida que el átomo de argón se movía lentamente, la fluctuación de posición debida a la energía del punto cero sería mucho menor que la resolución de 200 nanómetros (0,0002 mm) de un microscopio óptico. Es importante destacar que la velocidad de traslación del átomo de 14,43 micrones por segundo constituye toda su energía cinética retenida debido a que no se encuentra precisamente en el cero absoluto. Si el átomo precisamente estuviera en el cero absoluto, un empujón imperceptible debido a la energía del punto cero haría que se desviara muy levemente, pero el átomo estaría ubicado perpetuamente, en promedio, en el mismo lugar dentro del campo de vista. Esto es análogo a un barco al que se le ha apagado el motor y ahora se balancea ligeramente en aguas oceánicas relativamente tranquilas y sin viento; aunque el barco se desplace aleatoriamente de un lado a otro, permanece en el mismo lugar a largo plazo y no avanza en el agua. En consecuencia, un átomo que estuviera precisamente en el cero absoluto no estaría "inmóvil" y, sin embargo, una colección estadísticamente significativa de tales átomos tendría una energía cinética neta cero disponible para transferir a cualquier otra colección de átomos. Esto se debe a que, independientemente de la temperatura cinética de la segunda colección de átomos, ellos también experimentan los efectos de la energía de punto cero. Tales son las consecuencias de la mecánica estadística y la naturaleza de la termodinámica.
Movimientos internos de moléculas y energía interna

Como se mencionó anteriormente, hay otras formas en que las moléculas pueden sacudirse además de los tres grados de libertad de traslación que imbuyen a las sustancias con su temperatura cinética. Como puede verse en la animación de la derecha, las moléculas son objetos complejos; son una población de átomos y la agitación térmica puede tensar sus enlaces químicos internos de tres maneras diferentes: a través de la rotación, la longitud del enlace y los movimientos del ángulo del enlace; todos estos son tipos de grados de libertad internos. Esto diferencia a las moléculas de las sustancias monatómicas (que consisten en átomos individuales) como los gases nobles helio y argón, que tienen solo los tres grados de libertad de traslación (los ejes X, Y y Z). La energía cinética se almacena en moléculas' grados de libertad internos, lo que les da una temperatura interna. Aunque estos movimientos se denominan 'internos', las partes externas de las moléculas aún se mueven, como el movimiento de un globo de agua estacionario. Esto permite el intercambio bidireccional de energía cinética entre movimientos internos y movimientos de traslación con cada colisión molecular. En consecuencia, a medida que se elimina la energía interna de las moléculas, tanto su temperatura cinética (la energía cinética del movimiento de traslación) como su temperatura interna disminuyen simultáneamente en proporciones iguales. Este fenómeno se describe mediante el teorema de equipartición, que establece que para cualquier cantidad aparente de una sustancia en equilibrio, la energía cinética del movimiento de las partículas se distribuye uniformemente entre todos los grados de libertad activos disponibles para las partículas. Dado que la temperatura interna de las moléculas suele ser igual a su temperatura cinética, la distinción suele ser de interés solo en el estudio detallado de fenómenos de equilibrio termodinámico no local (LTE) como la combustión, la sublimación de sólidos y la difusión de gases calientes. en un vacío parcial.
La energía cinética almacenada internamente en las moléculas hace que las sustancias contengan más energía térmica a cualquier temperatura determinada y absorban energía interna adicional para un aumento de temperatura determinado. Esto se debe a que cualquier energía cinética que, en un instante dado, esté ligada a los movimientos internos, no contribuye a que las moléculas ' movimientos de traslación en ese mismo instante. Esta energía cinética adicional simplemente aumenta la cantidad de energía interna que absorbe la sustancia para un aumento de temperatura dado. Esta propiedad se conoce como capacidad calorífica específica de una sustancia.
Diferentes moléculas absorben diferentes cantidades de energía interna para cada aumento incremental de temperatura; es decir, tienen diferentes capacidades caloríficas específicas. La alta capacidad de calor específico surge, en parte, porque las moléculas de ciertas sustancias poseen más grados de libertad internos que otras. Por ejemplo, el nitrógeno a temperatura ambiente, que es una molécula diatómica, tiene cinco grados de libertad activos: los tres comprenden el movimiento de traslación más dos grados de libertad de rotación internamente. No es sorprendente que, de acuerdo con el teorema de equipartición, el nitrógeno tenga cinco tercios de la capacidad calorífica específica por mol (un número específico de moléculas) al igual que los gases monoatómicos. Otro ejemplo es la gasolina (ver tabla que muestra su capacidad calorífica específica). La gasolina puede absorber una gran cantidad de energía térmica por mol con solo un cambio de temperatura modesto porque cada molécula comprende un promedio de 21 átomos y, por lo tanto, tiene muchos grados de libertad internos. Incluso las moléculas más grandes y complejas pueden tener docenas de grados de libertad internos.
Difusión de energía térmica: entropía, fonones y electrones móviles de conducción
Conducción de calor es la difusión de energía térmica desde las partes calientes de un sistema hacia las partes frías. Un sistema puede ser una sola entidad a granel o una pluralidad de entidades a granel discretas. El término bulto en este contexto significa una cantidad estadísticamente significativa de partículas (que puede ser una cantidad microscópica). Cada vez que la energía térmica se difunde dentro de un sistema aislado, las diferencias de temperatura dentro del sistema disminuyen (y aumenta la entropía).
Un mecanismo particular de conducción de calor ocurre cuando el movimiento de traslación, el movimiento de partículas subyacente a la temperatura, transfiere el impulso de una partícula a otra en las colisiones. En los gases, estos movimientos de traslación son de la naturaleza que se muestra arriba en Fig. 1. Como se puede ver en esa animación, no solo el impulso (calor) se difunde por todo el volumen del gas a través de colisiones en serie, sino que moléculas o átomos enteros pueden avanzar hacia un nuevo territorio, trayendo consigo su energía cinética. En consecuencia, las diferencias de temperatura se igualan en todos los gases muy rápidamente, especialmente para átomos o moléculas ligeros; la convección acelera este proceso aún más.
El movimiento de traslación en sólidos, sin embargo, toma la forma de fonones (ver Fig. 4 a la derecha). Los fonones son paquetes de ondas cuantificadas y limitadas que viajan a la velocidad del sonido de una sustancia determinada. La forma en que interactúan los fonones dentro de un sólido determina una variedad de sus propiedades, incluida su conductividad térmica. En los sólidos eléctricamente aislantes, la conducción de calor basada en fonones es generalmente ineficiente y dichos sólidos se consideran aislantes térmicos (como vidrio, plástico, caucho, cerámica y roca). Esto se debe a que en los sólidos, los átomos y las moléculas están bloqueados en su lugar en relación con sus vecinos y no tienen libertad para moverse.
Sin embargo, los metales no se limitan únicamente a la conducción de calor basada en fonones. La energía térmica se conduce a través de los metales extraordinariamente rápido porque, en lugar de colisiones directas de molécula a molécula, la gran mayoría de la energía térmica se transmite a través de electrones de conducción muy ligeros y móviles. Esta es la razón por la que existe una correlación casi perfecta entre los metales & # 39; conductividad térmica y su conductividad eléctrica. Los electrones de conducción imbuyen a los metales con su extraordinaria conductividad porque están deslocalizados (es decir, no están vinculados a un átomo específico) y se comportan más bien como una especie de gas cuántico debido a los efectos de la energía de punto cero (para obtener más información sobre ZPE, consulte la Nota 1 a continuación). Además, los electrones son relativamente livianos con una masa en reposo de solo 1⁄1836 la de un protón. Esta es aproximadamente la misma proporción que una bala corta.22 (29 granos o 1,88 g) en comparación con el rifle que la dispara. Como escribió Isaac Newton con su tercera ley del movimiento,
Ley #3: Todas las fuerzas ocurren en pares, y estas dos fuerzas son iguales en magnitud y en dirección contraria.
Sin embargo, una bala acelera más rápido que un rifle con la misma fuerza. Dado que la energía cinética aumenta con el cuadrado de la velocidad, casi toda la energía cinética va hacia la bala, no hacia el rifle, aunque ambos experimentan la misma fuerza de los gases propulsores en expansión. De la misma manera, debido a que son mucho menos masivos, los electrones de conducción móviles transportan fácilmente la energía térmica. Además, debido a que están deslocalizados y son muy rápidos, la energía térmica cinética se conduce extremadamente rápido a través de metales con abundantes electrones de conducción.
Difusión de energía térmica: radiación de cuerpo negro
La radiación térmica es un subproducto de las colisiones que surgen de varios movimientos vibratorios de los átomos. Estas colisiones hacen que los electrones de los átomos emitan fotones térmicos (conocidos como radiación de cuerpo negro). Los fotones se emiten cada vez que se acelera una carga eléctrica (como sucede cuando colisionan nubes de electrones de dos átomos). Incluso moléculas individuales con temperaturas internas superiores al cero absoluto también emiten radiación de cuerpo negro de sus átomos. En cualquier cantidad a granel de una sustancia en equilibrio, los fotones de cuerpo negro se emiten en un rango de longitudes de onda en un espectro que tiene una forma similar a una curva de campana llamada curva de Planck (ver gráfico en Fig. 5 A la derecha). La parte superior de una curva de Planck (la longitud de onda de emitancia máxima) se encuentra en una parte particular del espectro electromagnético dependiendo de la temperatura del cuerpo negro. Las sustancias a temperaturas criogénicas extremas emiten en longitudes de onda de radio largas, mientras que las temperaturas extremadamente altas producen rayos gamma cortos (ver Tabla de temperaturas comunes).
La radiación de cuerpo negro difunde energía térmica a través de una sustancia a medida que los fotones son absorbidos por los átomos vecinos, transfiriendo impulso en el proceso. Los fotones de cuerpo negro también escapan fácilmente de una sustancia y pueden ser absorbidos por el entorno ambiental; la energía cinética se pierde en el proceso.
Como establece la ley de Stefan-Boltzmann, la intensidad de la radiación del cuerpo negro aumenta como la cuarta potencia de la temperatura absoluta. Por lo tanto, un cuerpo negro a 824 K (apenas para brillar en rojo opaco) emite 60 veces la potencia radiante que emite a 296 K (temperatura ambiente). Esta es la razón por la que uno puede sentir tan fácilmente el calor radiante de los objetos calientes a distancia. A temperaturas más altas, como las que se encuentran en una lámpara incandescente, la radiación de cuerpo negro puede ser el principal mecanismo por el cual la energía térmica escapa de un sistema.
Tabla de temperaturas termodinámicas
La siguiente tabla muestra varios puntos en la escala termodinámica, en orden de temperatura creciente.
| kelvin | Expedición de pico longitud de onda de fotones de cuerpo negro | |
| Absoluto cero (precisamente por definición) | 0 K | JUEGO |
| Medido frío temperatura | 450 pK | 6.400 km |
| Un ligero (precisamente por definición) | 0,001 K | 2.897 77 m (radio, banda FM) |
| radiación cósmica de microondas | 2.725 K | 1.063 mm (longitud de onda pico) |
| Punto triple del agua | 273.16 K | 10.6083 μm (long wavelength I.R.) |
| Temperatura estándar ISO 1 para la metrología de precisión (precisamente 20 °C por definición) | 293.15 K | 9.88495μm (long wavelength I.R.) |
| Lámpara incandescente | 2500 K | 1.16 μm (cerca de infrarrojos) |
| Superficie visible del Sol | 5778 K | 501.5 nm (luz verde) |
| Tornillo de relámpago canal | 28.000 K | 100 nm (luz ultravioleta) |
| El núcleo del Sol | 16 MK | 0.18 nm (rayos X) |
| Explosión termonuclear (temperatura pico) | 350 MK | 8.3 × 10−3 nm (rayos gamma) |
| Laboratorios Nacionales de Sandia ' Máquina Z | 2 GK | 1.4 × 10−3 nm (rayos gamma) |
| El núcleo de una estrella de alta masa en su último día | 3 GK | 1 × 10−3 nm (rayos gamma) |
| Merging binario neutronstar system | 350 GK | 8 × 10−6 nm (rayos gamma) |
| progenitores de la explosión de rayos gamma | 1 TK | 3 × 10−6 nm (rayos gamma) |
| El protón del CERN vs. nucleus collisions | 10 TK | 3 × 10−7 nm (rayos gamma) |
- ^ Para un verdadero cuerpo negro (que los filamentos de tungsteno no son). La emisividad de los filamentos de tungsteno es mayor en longitudes de onda más cortas, lo que los hace parecer más blancos.
- ^ El valor de 2500 K es aproximado.
- ^ a b Temperatura fotosférica efectiva.
- ^ Para un verdadero cuerpo negro (que el plasma no era). La emisión dominante de la máquina Z se originó en los electrones 40 MK (emisiones de rayos X blandos) dentro del plasma.
Cambios de calor de fase
La energía cinética del movimiento de las partículas es solo uno de los contribuyentes a la energía térmica total de una sustancia; otro son las transiciones de fase, que son la energía potencial de los enlaces moleculares que se pueden formar en una sustancia a medida que se enfría (como durante la condensación y la congelación). La energía térmica requerida para una transición de fase se llama calor latente. Este fenómeno puede comprenderse más fácilmente si se considera en sentido inverso: el calor latente es la energía necesaria para romper los enlaces químicos (como durante la evaporación y el derretimiento). Casi todo el mundo está familiarizado con los efectos de las transiciones de fase; por ejemplo, el vapor a 100 °C puede causar quemaduras graves mucho más rápido que el aire a 100 °C de un secador de pelo. Esto ocurre porque se libera una gran cantidad de calor latente a medida que el vapor se condensa en agua líquida sobre la piel.
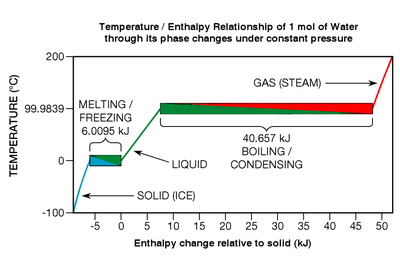
Aunque la energía térmica se libera o se absorbe durante las transiciones de fase, los elementos químicos puros, los compuestos y las aleaciones eutécticas no muestran ningún cambio de temperatura mientras los experimentan (ver Fig. 7, abajo a la derecha). Considere un tipo particular de transición de fase: fusión. Cuando un sólido se derrite, los enlaces químicos de la red cristalina se rompen; la sustancia está pasando de lo que se conoce como un estado más ordenado a un estado menos ordenado. En la fig. 7, el derretimiento del hielo se muestra dentro del cuadro inferior izquierdo que va de azul a verde.
En un punto termodinámico específico, el punto de fusión (que es 0 °C en un amplio rango de presión en el caso del agua), todos los átomos o moléculas se encuentran, en promedio, en el umbral máximo de energía que sus enlaces químicos pueden soportar. sin romper con la red. Los enlaces químicos son fuerzas de todo o nada: se mantienen firmes o se rompen; no hay estado intermedio. En consecuencia, cuando una sustancia está en su punto de fusión, cada julio de energía térmica añadida sólo rompe los enlaces de una cantidad específica de sus átomos o moléculas, convirtiéndolos en un líquido de exactamente la misma temperatura; no se agrega energía cinética al movimiento de traslación (que es lo que le da a las sustancias su temperatura). El efecto es similar al de las palomitas de maíz: a cierta temperatura, la energía térmica adicional no puede hacer que los granos se calienten más hasta que se complete la transición (explosión). Si el proceso se invierte (como en la congelación de un líquido), se debe eliminar la energía térmica de una sustancia.
Como se indicó anteriormente, la energía térmica requerida para una transición de fase se llama calor latente. En los casos específicos de fusión y congelación, se denomina entalpía de fusión o calor de fusión. Si los enlaces moleculares en una red cristalina son fuertes, el calor de fusión puede ser relativamente grande, típicamente en el rango de 6 a 30 kJ por mol para el agua y la mayoría de los elementos metálicos. Si la sustancia es uno de los gases monoatómicos (que tienen poca tendencia a formar enlaces moleculares), el calor de fusión es más modesto, oscilando entre 0,021 y 2,3 kJ por mol. En términos relativos, las transiciones de fase pueden ser eventos verdaderamente energéticos. Para derretir completamente el hielo a 0 °C en agua a 0 °C, se debe agregar aproximadamente 80 veces la energía térmica que se requiere para aumentar la temperatura de la misma masa de agua líquida en un grado Celsius. Los metales' las proporciones son aún mayores, típicamente en el rango de 400 a 1200 veces. Y la transición de fase de ebullición es mucho más enérgica que la congelación. Por ejemplo, la energía requerida para hervir o vaporizar completamente el agua (lo que se conoce como entalpía de vaporización) es aproximadamente 540 veces la requerida para un aumento de un grado.
La considerable entalpía de vaporización del agua es la razón por la que la piel puede quemarse tan rápido cuando el vapor se condensa sobre ella (en la Fig. 7 arriba); los vapores de agua (fase gaseosa) se licuan en la piel liberando una gran cantidad de energía (entalpía) al medio ambiente, incluida la piel, lo que provoca daños en la piel. En la dirección opuesta, esta es la razón por la cual la piel se siente fría cuando el agua líquida se evapora (un proceso que ocurre a una temperatura de bulbo húmedo por debajo del ambiente que depende de la humedad relativa); la evaporación del agua sobre la piel consume una gran cantidad de energía del medio ambiente, incluida la piel, lo que reduce la temperatura de la piel. La entalpía de vaporización altamente energética del agua también es un factor importante que explica por qué las cubiertas solares para piscinas (mantas aislantes flotantes que cubren las piscinas cuando no están en uso) son tan efectivas para reducir el calentamiento. costes: evitan la evaporación. (En otras palabras, tomar energía del agua cuando se evapora es limitado). Por ejemplo, la evaporación de solo 20 mm de agua de una piscina de 1,29 metros de profundidad enfría el agua 8,4 grados centígrados (15,1 °F).
Energía interna
La energía total de todos los movimientos internos y de traslación de las partículas, incluido el de los electrones de conducción, más la energía potencial de los cambios de fase, más la energía de punto cero de una sustancia constituyen la energía interna de la misma.

Energía interna en el cero absoluto
A medida que una sustancia se enfría, las diferentes formas de energía interna y sus efectos relacionados disminuyen simultáneamente en magnitud: el calor latente de las transiciones de fase disponibles se libera a medida que la sustancia cambia de un estado menos ordenado a un estado más ordenado; disminuyen los movimientos de traslación de átomos y moléculas (disminuye su energía cinética o temperatura); los movimientos internos de las moléculas disminuyen (disminuye su energía interna o temperatura); los electrones de conducción (si la sustancia es un conductor eléctrico) viajan algo más lento; y la longitud de onda de emitancia máxima de la radiación de cuerpo negro aumenta (la energía de los fotones disminuye). Cuando las partículas de una sustancia están lo más cerca posible del reposo total y retienen solo el movimiento mecánico cuántico inducido por ZPE (Zero Point Energy), la sustancia está a la temperatura del cero absoluto (T = 0).
Tenga en cuenta que mientras que el cero absoluto es el punto de temperatura termodinámica cero y también es el punto en el que las partículas constituyentes de la materia tienen un movimiento mínimo, el cero absoluto no es necesariamente el punto en el que una sustancia contiene energía interna cero; hay que ser muy preciso con lo que se entiende por energía interna. A menudo, todos los cambios de fase que pueden ocurrir en una sustancia, habrán ocurrido antes de que alcance el cero absoluto. Sin embargo, este no es siempre el caso. En particular, T = 0 el helio permanece líquido a presión ambiente (Fig. 9 a la derecha) y debe estar bajo una presión de al menos 25 bar (2,5 MPa) para cristalizar. Esto se debe a que el calor de fusión del helio (la energía necesaria para derretir el hielo de helio) es tan bajo (solo 21 julios por mol) que el efecto de inducción de movimiento de la energía de punto cero es suficiente para evitar que se congele a temperaturas más bajas. presiones
Otra complicación es que muchos sólidos cambian su estructura cristalina a arreglos más compactos a presiones extremadamente altas (hasta millones de bares o cientos de gigapascales). Estas se conocen como transiciones de fase sólido-sólido en las que el calor latente se libera a medida que una red cristalina cambia a una más compacta, termodinámicamente favorable.
Las complejidades anteriores crean declaraciones generales bastante engorrosas con respecto a la energía interna en sustancias T = 0. Sin embargo, independientemente de la presión, lo que puede decirse es que en el cero absoluto, todos los sólidos con una red cristalina de energía más baja, como aquellos con una disposición de empaquetamiento más cercano (ver Fig. 8, arriba a la izquierda) contienen energía interna mínima, reteniendo solo la que se debe al fondo siempre presente de energía de punto cero. También se puede decir que para una sustancia dada en presión constante, el cero absoluto es el punto de menor entalpía (una medida del potencial de trabajo que tiene en cuenta la energía interna, la presión y el volumen). Por último, siempre es cierto que todas las sustancias T = 0 contienen energía térmica cinética cero.
Aplicaciones prácticas de la temperatura termodinámica
La temperatura termodinámica es útil no solo para los científicos, también puede ser útil para los legos en muchas disciplinas que involucran gases. Al expresar las variables en términos absolutos y aplicar la ley de proporcionalidad temperatura/presión de Gay-Lussac, las soluciones a los problemas cotidianos son sencillas; por ejemplo, calcular cómo un cambio de temperatura afecta la presión dentro de un neumático de automóvil. Si el neumático tiene una presión manométrica en frío de 200 kPa, entonces su presión absoluta es de 300 kPa. La temperatura ambiente ("fría" en términos de neumáticos) es de 296 K. Si la temperatura de los neumáticos es 20 °C más alta (20 kelvin), la solución se calcula como 316 K/296 K = 6,8% mayor temperatura termodinámica y presión absoluta; es decir, una presión absoluta de 320 kPa, que es una presión manométrica de 220 kPa.
Relación con la ley de los gases ideales
La temperatura termodinámica está íntimamente ligada a la ley de los gases ideales y sus consecuencias. Se puede vincular también a la segunda ley de la termodinámica. Se puede demostrar que la temperatura termodinámica tiene propiedades especiales y, en particular, se puede ver que se define de manera única (hasta algún factor multiplicativo constante) al considerar la eficiencia de los motores térmicos idealizados. Así, la razón T2/T1 de dos temperaturas T 1 y T2 es el mismo en todas las escalas absolutas.
Estrictamente hablando, la temperatura de un sistema está bien definida solo si está en equilibrio térmico. Desde un punto de vista microscópico, un material está en equilibrio térmico si la cantidad de calor entre sus partículas individuales se cancela. Hay muchas escalas posibles de temperatura, derivadas de una variedad de observaciones de fenómenos físicos.
En pocas palabras, las diferencias de temperatura dictan la dirección del calor entre dos sistemas de modo que su energía combinada se distribuya al máximo entre sus estados más bajos posibles. Llamamos a esta distribución "entropía". Para entender mejor la relación entre temperatura y entropía, considere la relación entre calor, trabajo y temperatura ilustrada en la máquina térmica de Carnot. El motor convierte el calor en trabajo dirigiendo un gradiente de temperatura entre una fuente de calor de mayor temperatura, TH, y un disipador de calor de menor temperatura, T C, a través de un pistón lleno de gas. El trabajo realizado por ciclo es igual en magnitud al calor neto absorbido, que es la suma del calor qH absorbido por el motor de la fuente de alta temperatura, más el calor residual emitido por el motor, qC < 0. La eficiencia del motor es el trabajo dividido por el calor introducido en el sistema o
El teorema de Carnot establece que todos los motores reversibles que operan entre los mismos depósitos de calor son igualmente eficientes. Así, cualquier máquina térmica reversible que funcione entre las temperaturas T1 y T2 debe tener la misma eficiencia, es decir decir, la eficiencia es función de solo las temperaturas
Además, un motor térmico reversible operando entre un par de depósitos térmicos a temperaturas T1 y T3 debe tener la misma eficiencia que uno formado por dos ciclos, uno entre T1 y otro (intermedio) de temperatura T2 , y la segunda entre T2 y T3. Si este no fuera el caso, entonces la energía (en forma de q) se desperdiciará o se ganará, lo que resultará en diferentes eficiencias generales cada vez que un ciclo se divida en ciclos componentes; claramente, un ciclo puede estar compuesto por cualquier número de ciclos más pequeños como elección de diseño del motor, y cualquier motor reversible entre el mismo depósito en T1 y T3 debe ser igualmente eficiente independientemente del diseño del motor.
Si elegimos motores tales que el trabajo realizado por el motor de un ciclo y el motor de dos ciclos sea el mismo, entonces la eficiencia de cada motor térmico se escribe como se muestra a continuación.
- .. 1=1− − Silencioq3SilencioSilencioq1Silencio=1− − f()T1,T3){displaystyle eta ##{1}=1-{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}=1-f(T_{1},T_{3}}},
- .. 2=1− − Silencioq2SilencioSilencioq1Silencio=1− − f()T1,T2){displaystyle eta ##{2}=1-{frac {fnK_} {cH00}}}=1-f(T_{1},T_{2}}}},
- .. 3=1− − Silencioq3SilencioSilencioq2Silencio=1− − f()T2,T3){displaystyle eta ##{3}=1-{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}=1-f(T_{2},T_{3}}}.
Aquí, el motor 1 es el motor de un ciclo, y los motores 2 y 3 hacen el motor de dos ciclos donde hay el depósito intermedio en T2. También hemos utilizado el hecho de que el calor q2{displaystyle q_{2} pasa por el depósito térmico intermedio en T2{displaystyle T_{2} sin perder su energía. (I.e., q2{displaystyle q_{2} no se pierde durante su paso por el embalse en T2{displaystyle T_{2}.) Este hecho puede ser probado por lo siguiente.
- .. 2=1− − Silencioq2SilencioSilencioq1Silencio→ → Silenciow2Silencio=Silencioq1Silencio− − Silencioq2Silencio,.. 3=1− − Silencioq3SilencioSilencioq2Alternativa Alternativa Silencio→ → Silenciow3Silencio=Silencioq2Alternativa Alternativa Silencio− − Silencioq3Silencio,Silenciow2Silencio+Silenciow3Silencio=()Silencioq1Silencio− − Silencioq2Silencio)+()Silencioq2Alternativa Alternativa Silencio− − Silencioq3Silencio),.. 1=1− − Silencioq3SilencioSilencioq1Silencio=()Silenciow2Silencio+Silenciow3Silencio)Silencioq1Silencio=()Silencioq1Silencio− − Silencioq2Silencio)+()Silencioq2Alternativa Alternativa Silencio− − Silencioq3Silencio)Silencioq1Silencio.{displaystyle {begin{aligned} }_{2}=1-{frac {fnK} {fnK} {fnh}}to}t} - ¿Qué? }_{3}=1-{frac {fnK} {fnK} {f}} {fnK}} {f}}} {to}}} {to}}} {to}}}} {f}}}} {to}}}}} {to}} {to}} {to}}}}} {to}}}}}}}} {to}}}} {to}}}}}}} {to}}}}}}}}}}}}}}}} {to}}}}}}}}}}} {to}}}}}}}}}}} {to}}}}}}}}}}}}}}}}} {to {to}}}}} {to}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {to}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {} {}} {}} {}}} {}}} {}} {}}} {}} {}}} {}} {}} {}} {}} {}}} {}} {}}}} {} {}} {}}}}} {}}}}}} {}}}}}}}}}} {}}}}}}} {}}}}}}}}} {}}}}}}} {}}}}}}} {}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}} }_{1}=1-{frac {fnK} {fnK} {fnK} {f}}}h}h} {fnK}} {f}} {f}} {f}} {f}}} {fn}}} {f}}}} {f}}} {f}}}}}} {f}}}}}}}}}\\\f}}}}}}}}}}}}\\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\fn}}}}}}}\\\\\\\\\fn}}}}}}}}}}}}}}}}}}\\\\\\\fn}}}}}}}}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {} {}} {}} {}} {}} {} {}} {} {}} {}} {}} {} {}} {}}} {}} {}}} {}} {}}}} {} {}} {}}}}} {}}}}}} {}}}}}}} {}}}}}} {}}}}}}}} {}}}}}}} {}}}}} {}}} {}} {}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}} {}}}} {}}}}}}}} {}}}}}} {} {}}}} {}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}
Para tener la consistencia en la última ecuación, el calor q2{displaystyle q_{2} fluido del motor 2 al depósito intermedio debe ser igual al calor q2Alternativa Alternativa {displaystyle q_{2}{*} fluido desde el embalse hasta el motor 3.
Con este entendimiento de q1, q2 y q3, matemáticamente,
Pero dado que la primera función NO es una función de T2, el producto de las dos funciones finales DEBE i> da como resultado la eliminación de T2 como variable. Por lo tanto, la única forma es definir la función f de la siguiente manera:
Es decir, la relación de calor intercambiado es una función de las temperaturas respectivas a las que ocurren. Podemos elegir cualquier función monotónica para nuestra g()T){displaystyle g(T)}; es una cuestión de conveniencia y convención que elegimos g()T)=T{displaystyle g(T)=T}. Eligiendo entonces uno Temperatura de referencia fija (es decir, triple punto de agua), establecemos la escala de temperatura termodinámica.
Tal definición coincide con la de la derivación del gas ideal; también es esta definición de la temperatura termodinámica la que nos permite representar la eficiencia de Carnot en términos de TH y TC, y de ahí derivar que el ciclo de Carnot (completo) es isoentrópico:
Al sustituir esto en nuestra primera fórmula de eficiencia, se obtiene una relación en términos de temperatura:
Note que para TC = 0 la eficiencia es 100% y que la eficiencia se hace mayor al 100% para TC 0, que es irrealista. La subcontratación 1 del lado derecho de la Ecuación (4) y la parte media da qCqH=− − TCTH{displaystyle {frac {f} {f} {f}}}=-{frac}} {f} {f}} {f}}} {f}} {f}}} {f}}}} {f}} {f}}}} {f}f}f}f}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}\\\\f}f} {f}f}f}f}f}\f}}\\f}f}}\\f}f}f}f}f}f}f}f}f}}f}f}\f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}}}}}fn {T_{text{C} {T_{H}}} {f}} {f}} {f}} {f}}} {f}}}} {f}}}} {f}}}}}}}} {f}}}}}}}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { y así
La generalización de esta ecuación es el teorema de Clausius, que propone la existencia de una función estatal S{displaystyle S. (es decir, una función que depende sólo del estado del sistema, no de cómo llegó a ese estado) definido (hasta una constante aditiva) por
dS=dqrevT,{displaystyle dS={frac {m\mh00} ♪♪ | ()5) |
donde el subscript rev indica la transferencia de calor en un proceso reversible. La función S{displaystyle S. es la entropía del sistema, mencionado anteriormente, y el cambio de S{displaystyle S. alrededor de cualquier ciclo es cero (como es necesario para cualquier función estatal). La Ecuación 5 se puede reorganizar para obtener una definición alternativa de temperatura en términos de entropía y calor (para evitar un bucle lógico, primero debemos definir entropía a través de la mecánica estadística):
Para un sistema de volumen constante (por lo que no hay trabajo mecánico W{displaystyle W.) en la que la entropía S{displaystyle S. es una función S()E){displaystyle S(E)} de su energía interna E{displaystyle E}, dE=dqrev{displaystyle dE=dq_{rev} y la temperatura termodinámica T{displaystyle T} por lo tanto,
Historia
1702-1703: Guillaume Amontons (1663-1705) publicó dos artículos que pueden utilizarse para acreditarlo como el primer investigador en deducir la existencia de una escala de temperatura fundamental (termodinámica) con un cero absoluto. Hizo el descubrimiento mientras se esforzaba por mejorar los termómetros de aire que se usaban en ese momento. Sus termómetros de tubo en J comprendían una columna de mercurio que estaba sostenida por una masa fija de aire atrapado dentro de la parte de detección del termómetro. En términos termodinámicos, sus termómetros se basaban en la relación volumen/temperatura del gas bajo presión constante. Sus mediciones del punto de ebullición del agua y el punto de fusión del hielo mostraron que, independientemente de la masa de aire atrapada dentro de sus termómetros o del peso del mercurio que soportaba el aire, la reducción del volumen de aire en el punto de hielo siempre fue la misma proporción.. Esta observación lo llevó a postular que una reducción suficiente de la temperatura reduciría el volumen de aire a cero. De hecho, sus cálculos proyectaron que el cero absoluto equivalía a −240 °C, solo 33,15 grados por debajo del valor real de −273,15 °C. El descubrimiento de Amonton de una relación uno a uno entre la temperatura absoluta y la presión absoluta fue redescubierto un siglo después y popularizado dentro de la comunidad científica por Joseph Louis Gay-Lussac. Hoy en día, este principio de la termodinámica se conoce comúnmente como ley de Gay-Lussac pero también se conoce como ley de Amonton.
1742: Anders Celsius (1701-1744) creó un "al revés" versión de la escala de temperatura Celsius moderna. En la escala original de Celsius, cero representaba el punto de ebullición del agua y 100 representaba el punto de fusión del hielo. En su artículo Observaciones de dos grados persistentes en un termómetro, relató sus experimentos que mostraban que el punto de fusión del hielo no se veía afectado por la presión. También determinó con notable precisión cómo variaba el punto de ebullición del agua en función de la presión atmosférica. Propuso que el cero en su escala de temperatura (el punto de ebullición del agua) se calibrara a la presión barométrica media al nivel medio del mar.
1744: coincidiendo con la muerte de Anders Celsius, el famoso botánico Carl Linnaeus (1707-1778) invirtió efectivamente la escala de Celsius al recibir su primer termómetro con una escala donde el cero representaba el punto de fusión del hielo y 100 representaba el punto de ebullición del agua. El termómetro de Linnaeus hecho a medida, para usar en sus invernaderos, fue fabricado por Daniel Ekström, el principal fabricante de instrumentos científicos de Suecia en ese momento. Durante los siguientes 204 años, las comunidades científicas y de termometría de todo el mundo se refirieron a esta escala como la escala centígrada. Las temperaturas en la escala centígrada a menudo se informaban simplemente como grados o, cuando se deseaba una mayor especificidad, grados centígrados. El símbolo de los valores de temperatura en esta escala era °C (en varios formatos a lo largo de los años). Debido a que el término centígrado también era el nombre en francés de una unidad de medida angular (una centésima parte de un ángulo recto) y tenía una connotación similar en otros idiomas, el término "grado centesimal& #34; se utilizó cuando los organismos internacionales de normalización, como la Oficina Internacional de Pesos y Medidas (Bureau international des poids et mesures) (BIPM), requerían un lenguaje muy preciso e inequívoco. La 9ª CGPM (Conferencia General de Pesos y Medidas (Conférence générale des poids et mesures) y el CIPM (Comité Internacional de Pesos y Medidas (Comité international des poids et mesures) adoptado formalmente grado Celsius (símbolo: °C) en 1948.
1777: En su libro Pyrometrie (Berlín: Haude & Spener, 1779) completado cuatro meses antes de su muerte, Johann Heinrich Lambert (1728–1777), a veces incorrectamente llamado Joseph Lambert, propuso una escala de temperatura absoluta basada en la relación presión/temperatura de un volumen fijo de gas. Esto es distinto de la relación volumen/temperatura del gas bajo presión constante que Guillaume Amontons descubrió 75 años antes. Lambert afirmó que el cero absoluto era el punto en el que una simple extrapolación en línea recta alcanzaba la presión del gas cero y era igual a -270 °C.
Alrededor de 1787: A pesar del trabajo de Guillaume Amontons 85 años antes, a Jacques Alexandre César Charles (1746–1823) se le atribuye a menudo el descubrimiento, pero no la publicación, de que el volumen de un gas bajo constante la presión es proporcional a su temperatura absoluta. La fórmula que creó fue V1/T1 = V2/T2.
1802: Joseph Louis Gay-Lussac (1778–1850) publicó un trabajo (reconociendo las notas de laboratorio inéditas de Jacques Charles quince años antes) que describe cómo el volumen de gas bajo presión constante cambia linealmente con su temperatura absoluta (termodinámica). Este comportamiento se llama Ley de Charles y es una de las leyes de los gases. Las suyas son las primeras fórmulas conocidas que utilizan el número 273 para el coeficiente de expansión del gas en relación con el punto de fusión del hielo (lo que indica que el cero absoluto equivalía a -273 °C).
1848: William Thomson, (1824–1907), también conocido como Lord Kelvin, escribió en su artículo, On an Absolute Thermometric Scale, sobre la necesidad de una escala donde frío infinito (cero absoluto) era el punto cero de la escala, y que usaba el grado Celsius para su incremento unitario. Al igual que Gay-Lussac, Thomson calculó que el cero absoluto equivalía a -273 °C en los termómetros de aire de la época. Esta escala absoluta se conoce hoy como la escala de temperatura termodinámica Kelvin. Cabe destacar que el valor de Thomson de −273 en realidad se derivó de 0,00366, que era el coeficiente de expansión aceptado de gas por grado Celsius en relación con el punto de hielo. El inverso de −0,00366 expresado con cinco dígitos significativos es −273,22 °C, que está muy cerca del valor real de −273,15 °C.
1859: Macquorn Rankine (1820–1872) propuso una escala de temperatura termodinámica similar a la de William Thomson pero que usaba el grado Fahrenheit para su incremento de unidad. Esta escala absoluta se conoce hoy como la escala de temperatura termodinámica de Rankine.
1877–1884: Ludwig Boltzmann (1844–1906) realizó importantes contribuciones a la termodinámica a través de la comprensión del papel que desempeñaban la cinética de partículas y la radiación del cuerpo negro. Su nombre ahora se une a varias de las fórmulas utilizadas hoy en día en termodinámica.
Alrededor de 1930: Los experimentos de termometría de gases cuidadosamente calibrados al punto de fusión del hielo y el punto de ebullición del agua mostraron que el cero absoluto equivalía a −273,15 °C.
1948: La Resolución 3 de la 9.ª CGPM (Conférence Générale des Poids et Mesures, también conocida como Conferencia General sobre Pesos y Medidas) fijó el punto triple del agua en exactamente 0,01 °C. En este momento, el punto triple aún no tenía una definición formal para su valor equivalente en kelvin, que la resolución declaró 'se fijará en una fecha posterior'. La implicación es que si el valor del cero absoluto medido en la década de 1930 era realmente −273,15 °C, entonces el punto triple del agua (0,01 °C) equivalía a 273,16 K. Además, tanto el CIPM (Comité international des poids et mesures, también conocido como el Comité Internacional de Pesas y Medidas) y la CGPM adoptaron formalmente el nombre Celsius para el grado Celsius y el Escala de temperatura Celsius.
1954: La resolución 3 de la 10.ª CGPM le dio a la escala Kelvin su definición moderna al elegir el punto triple del agua como su punto de definición superior (sin cambiar el cero absoluto como punto nulo) y asignándole una temperatura de precisamente 273,16 kelvins (lo que en realidad se escribió 273,16 grados Kelvin en ese momento). Esto, en combinación con la Resolución 3 de la 9.ª CGPM, tuvo el efecto de definir el cero absoluto como exactamente cero kelvin y −273,15 °C.
1967/1968: La Resolución 3 de la 13ª CGPM renombró el incremento unitario de temperatura termodinámica kelvin, símbolo K, reemplazando grado absoluto, símbolo °K. Además, considerando útil definir más explícitamente la magnitud del incremento unitario, la 13.ª CGPM también decidió en la Resolución 4 que "El kelvin, unidad de temperatura termodinámica, es la fracción 1/273,16 de la temperatura termodinámica del triple punto de agua".
2005: El CIPM (Comité International des Poids et Mesures, también conocido como Comité Internacional de Pesos y Medidas) afirmó que para efectos de delimitar la temperatura del punto triple del agua, el La definición de la escala de temperatura termodinámica Kelvin se referiría al agua que tiene una composición isotópica definida como exactamente igual a la especificación nominal del agua oceánica media estándar de Viena.
2019: En noviembre de 2018, la 26.ª Conferencia General sobre Pesas y Medidas (CGPM) cambió la definición de Kelvin fijando la constante de Boltzmann a 1,380649×10−23 cuando se expresa en la unidad J/K. Este cambio (y otros cambios en la definición de unidades SI) se hizo efectivo en el 144 aniversario de la Convención del Metro, el 20 de mayo de 2019.
Contenido relacionado
Lona de Turing
Partícula (desambiguación)
PCHP