Temperatura potencial equivalente

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Temperatura potencial equivalente, comúnmente denominado theta-e $left(theta _{e}right)$ , es una cantidad que se conserva durante los cambios a la presión de un paquete de aire (es decir, durante los movimientos verticales en la atmósfera), incluso si el vapor de agua se condensa durante ese cambio de presión. Por lo tanto, es más conservado que la temperatura potencial ordinaria, que permanece constante sólo para movimientos verticales insaturados (cambios de presión).

$theta _{e}$ es la temperatura que un paquete de aire alcanzaría si todo el vapor de agua en el paquete fuese para condensar, liberando su calor latente, y el paquete fue traído a diabaticamente a una presión de referencia estándar, generalmente 1000 hPa (1000 mbar) que es aproximadamente igual a la presión atmosférica a nivel del mar.

Su uso en la estimación de la estabilidad atmosférica

Estabilidad del fluido incompresible

Al igual que una pelota en equilibrio en la cima de una colina, el fluido más denso que se encuentra sobre un fluido menos denso sería dinámicamente inestable: los movimientos de vuelco (convección) pueden bajar el centro de gravedad y, por lo tanto, ocurrirán espontáneamente, produciendo rápidamente una estratificación estable que es por lo tanto, la condición observada casi todo el tiempo. La condición para la estabilidad de un fluido incompresible es que la densidad disminuya monótonamente con la altura.

Estabilidad del aire comprimible: temperatura potencial

Si un fluido es comprimible como el aire, el criterio para la estabilidad dinámica involucra la densidad potencial, la densidad del fluido a una presión de referencia fija. Para un gas ideal (ver leyes de los gases), el criterio de estabilidad para una columna de aire es que la temperatura potencial aumenta monótonamente con la altura.

Para entender esto, considere la convección seca en la atmósfera, donde la variación vertical de la presión es sustancial y el cambio de temperatura adiabático es importante: a medida que una porción de aire se mueve hacia arriba, la presión ambiental cae, lo que hace que la porción se expanda. Parte de la energía interna del paquete se usa para hacer el trabajo requerido para expandirse contra la presión atmosférica, por lo que la temperatura del paquete desciende, aunque no haya perdido calor. Por el contrario, una parcela que se hunde se comprime y se calienta aunque no se le agregue calor.

El aire en la cima de una montaña suele ser más frío que el aire en el valle de abajo, pero la disposición no es inestable: si una porción de aire del valle fuera levantada de alguna manera hasta la cima de la montaña, cuando llegara sería incluso más frío que el aire que ya está allí, debido al enfriamiento adiabático; sería más pesado que el aire ambiente y se hundiría hacia su posición original. De manera similar, si un paquete de aire frío de la cima de la montaña hiciera el viaje hacia el valle, llegaría más cálido y liviano que el aire del valle y flotaría de regreso a la montaña.

Entonces, el aire frío que se encuentra sobre el aire caliente puede ser estable, siempre que la disminución de la temperatura con la altura sea menor que la tasa de variación adiabática; la cantidad dinámicamente importante no es la temperatura, sino la temperatura potencial: la temperatura que tendría el aire si se lo llevara adiabáticamente a una presión de referencia. El aire alrededor de la montaña es estable porque el aire en la parte superior, debido a su menor presión, tiene una temperatura potencial más alta que el aire más cálido que se encuentra debajo.

Efectos de la condensación del agua: temperatura potencial equivalente

Una porción ascendente de aire que contiene vapor de agua, si se eleva lo suficiente, alcanza su nivel elevado de condensación: se satura con vapor de agua (ver relación Clausius-Clapeyron). Si la porción de aire continúa ascendiendo, el vapor de agua se condensa y libera su calor latente al aire circundante, compensando parcialmente el enfriamiento adiabático. Por lo tanto, una parcela de aire saturada se enfría menos que una seca a medida que asciende (su temperatura cambia con la altura en la tasa de gradiente adiabático húmedo, que es menor que la tasa de gradiente adiabático seco). Tal paquete de aire saturado puede lograr flotabilidad y, por lo tanto, acelerar aún más hacia arriba, una condición fuera de control (inestabilidad), incluso si la temperatura potencial aumenta con la altura. La condición suficiente para que una columna de aire sea absolutamente estable, incluso con respecto a los movimientos convectivos saturados, es que la temperatura potencial equivalente debe aumentar monótonamente con la altura.

Fórmula

La definición de la temperatura potencial equivalente es:

{displaystyle theta _{e}=Tleft({frac {p_{0}}{p}}right)^{R_{d}/(c_{pd}+r_{t}c)}H^{-r_{v}R_{v}/(c_{pd}+r_{t}c)}exp left[{frac {L_{v}r_{v}}{(c_{pd}+r_{t}c)T}}right]}

Dónde:

$T$ es la temperatura [K] del aire a presión $p$ ,
$p_{0}$ es una presión de referencia que se toma como 1000 hPa,
$p$ es la presión en el punto,
$R_d$ y $R_{v}$ son las constantes específicas de gas de aire seco y de vapor de agua, respectivamente,
$c_{{pd}}$ y $c$ son las capacidades de calor específicas del aire seco y del agua líquida, respectivamente,
$r_{t}$ y ${displaystyle r_{v}}$ son los coeficientes totales de mezcla de agua y vapor de agua, respectivamente,
$H$ es la humedad relativa,
$L_{v}$ es el calor latente de la vapourización del agua.

Se utilizan varias formulaciones aproximadas para calcular la temperatura potencial equivalente, ya que no es fácil calcular integraciones a lo largo del movimiento de la parcela. Bolton (1980) da una revisión de tales procedimientos con estimaciones de error. Su fórmula de mejor aproximación se usa cuando se necesita precisión:

theta _{e}=theta _{{L}}exp left[left({frac {3036}{T_{L}}}-1.78right)rleft(1+0.448rright)right]

theta _{{L}}=Tleft({frac {p_{0}}{p-e}}right)^{{kappa _{d}}}left({frac {T}{T_{L}}}right)^{{0.28r}}

T_{L}={frac {1}{{frac {1}{T_{d}-56}}+{frac {log _{e}(T/T_{d})}{800}}}}+56

Dónde:

$theta _{L}$ es (dry) temperatura potencial [K] en el nivel de condensación elevado (LCL),
$T_{L}$ es (aproximada) temperatura [K] en LCL,
$T_{d}$ es temperatura de punto de rocío a presión $p$ ,
$e$ es la presión de vapor de agua (para obtener $theta _{{L}}$ para aire seco),
$kappa _{d}=R_{d}/c_{{pd}}$ es la relación de la constante de gas específica al calor específico del aire seco a presión constante (0.2854),
$r$ es la relación de mezcla de vapor de agua por masa [kg/kg] (a veces el valor se da en [g/kg] y que debe dividirse en 1000).

Una fórmula un poco más teórica se usa comúnmente en literatura como Holton (1972) cuando la explicación teórica es importante:

theta _{e}approx theta _{L}exp left[{frac {r_{s}(T_{L})L_{v}(T_{L})}{c_{{pd}}T_{L}}}right]

Dónde:

$r_{s}(T_{L})$ es la relación de mezcla saturada del agua a temperatura $T_{L}$ , la temperatura en el nivel de saturación del aire,
$L_{v}(T_{L})$ es calor latente de evaporación a temperatura $T_{L}$ (2406 kJ/kg {at 40 °C} to 2501 kJ/kg {at 0 °C}), and
$c_{{pd}}$ es calor específico del aire seco a presión constante (1005.7 J/(kg·K)).

Se utiliza más fórmula simplificada (por ejemplo, Stull 1988 §13.1 p. 546) para la simplicidad, si es deseable evitar la computación $T_{L}$ :

{displaystyle theta _{e}=T_{e}left({frac {p_{0}}{p}}right)^{kappa _{d}}approx left(T+{frac {L_{v}}{c_{pd}}}rright)left({frac {p_{0}}{p}}right)^{frac {R_{d}}{c_{pd}}}}

Dónde:

$T_{e}$ = temperatura equivalente
$R_d$ = constante de gas específico para el aire (287.04 J/(kg·K))

Uso

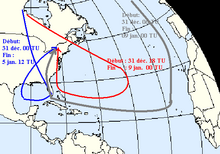
Esto se aplica en la escala sinóptica para la caracterización de masas de aire. Por ejemplo, en un estudio de la tormenta de hielo de América del Norte de 1998, los profesores Gyakum (Universidad McGill, Montreal) y Roebber (Universidad de Wisconsin-Milwaukee) demostraron que las masas de aire involucradas se originaron en el Ártico alto a una altitud de 300 a 400 hPa la semana anterior, descendieron hacia la superficie a medida que avanzaban hacia los trópicos, luego regresaron a lo largo del valle de Mississippi hacia el valle de St. Lawrence. Las trayectorias posteriores se evaluaron utilizando las temperaturas de potencial equivalente constante.

En la mesoescala, la temperatura potencial equivalente también es una medida útil de la estabilidad estática de la atmósfera no saturada. En condiciones normales, establemente estratificadas, la temperatura potencial aumenta con la altura,

0}" xmlns="http://www.w3.org/1998/Math/MathML">∂ ∂ Silencio Silencio e∂ ∂ z■0{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} theta ¿Qué?0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/16875e5b5e08c5e9260c3fc34bab78a80b9f8cd4" style="vertical-align: -2.005ex; width:8.504ex; height:5.509ex;"/>

y se suprimen los movimientos verticales. Si la temperatura potencial equivalente disminuye con la altura,

<math alttext="{displaystyle {frac {partial theta _{e}}{partial z}}∂ ∂ Silencio Silencio e∂ ∂ z.0{fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} theta ¿Qué?<img alt="{frac {partial theta _{e}}{partial z}}

la atmósfera es inestable a los movimientos verticales y es probable que haya convección. Las situaciones en las que la temperatura potencial equivalente disminuye con la altura, lo que indica inestabilidad en el aire saturado, son bastante comunes.

Contenido relacionado

Más resultados...