Temperatura curie

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Temperatura por encima de la cual las propiedades magnéticas cambian

Gráfico 1 Debajo de la temperatura Curie, los giros magnéticos vecinos alinean paralelamente entre sí en ferromagnet en ausencia de un campo magnético aplicado

Gráfico 2 Sobre la temperatura de Curie, los giros magnéticos se alinean aleatoriamente en un paramagnet a menos que se aplique un campo magnético

En física y ciencia de los materiales, la temperatura de Curie (T_C), o punto de Curie, es la temperatura por encima de la cual ciertos materiales pierden sus propiedades magnéticas permanentes, que pueden (en la mayoría de los casos) ser reemplazadas por magnetismo inducido. La temperatura de Curie lleva el nombre de Pierre Curie, quien demostró que el magnetismo se perdía a una temperatura crítica.

La fuerza del magnetismo está determinada por el momento magnético, un momento dipolar dentro de un átomo que se origina a partir del momento angular y el espín de los electrones. Los materiales tienen diferentes estructuras de momentos magnéticos intrínsecos que dependen de la temperatura; la temperatura de Curie es el punto crítico en el que los momentos magnéticos intrínsecos de un material cambian de dirección.

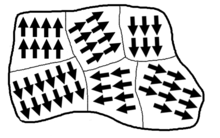
El magnetismo permanente es causado por la alineación de los momentos magnéticos y el magnetismo inducido se crea cuando los momentos magnéticos desordenados se ven obligados a alinearse en un campo magnético aplicado. Por ejemplo, los momentos magnéticos ordenados (ferromagnéticos, Figura 1) cambian y se desordenan (paramagnéticos, Figura 2) a la temperatura de Curie. Las temperaturas más altas debilitan los imanes, ya que el magnetismo espontáneo solo ocurre por debajo de la temperatura de Curie. La susceptibilidad magnética por encima de la temperatura de Curie se puede calcular a partir de la ley de Curie-Weiss, que se deriva de la ley de Curie.

En analogía con los materiales ferromagnéticos y paramagnéticos, la temperatura de Curie también se puede utilizar para describir la transición de fase entre ferroelectricidad y paraelectricidad. En este contexto, el parámetro de orden es la polarización eléctrica que va de un valor finito a cero cuando la temperatura se incrementa por encima de la temperatura de Curie.

Temperatura Curie de los materiales
Material	Curie temperatura (K)	°C	°F
Iron (Fe)	1043	770	1418
Cobalto (Co)	1400	1130	2060
Nickel (Ni)	627	354	669
Gadolinium (Gd)	292	19	66
Dysprosium (Dy)	88	−185.2	−301.3
bismuturo de manganés (MnBi)	630	357	674
Manganese antimonide (MnSb)	587	314	597
óxido de cromo (IV) (CrO₂)	386	113	235
Arsenida manganesa (MnAs)	318	45	113
Óxido de Europium (EuO)	69	−204.2	−335,5
óxido de hierro (III)₂O₃)	948	675	1247
óxido de hierro (II,III) (FeOFe₂O₃)	858	585	1085
NiO-Fe₂O₃	858	585	1085
CuO-Fe₂O₃	728	455	851
MgO-Fe₂O₃	713	440	824
MnO-Fe₂O₃	573	300	572
Granate de hierro de Yttrium (Y₃Fe₅O₁₂)	560	287	548
imanes de neodimio	583–673	310–400	590–752
Alnico	973–1133	700 a 860	1292–1580
imanes Samarium–cobalto	993–1073	720–800	1328 a 1472
Ferrite de estroncio	723	450	842

Momentos magnéticos

Los momentos magnéticos son momentos dipolares permanentes dentro de un átomo que comprenden el momento angular del electrón y el espín por la relación μ_l = el/2m_e, donde m_e es la masa de un electrón, μ_l es el momento magnético y l es el momento angular; esta relación se denomina relación giromagnética.

Los electrones en un átomo aportan momentos magnéticos de su propio momento angular y de su momento orbital alrededor del núcleo. Los momentos magnéticos del núcleo son insignificantes en contraste con los momentos magnéticos de los electrones. Las contribuciones térmicas dan como resultado electrones de mayor energía que alteran el orden y destruyen la alineación entre los dipolos.

Los materiales ferromagnéticos, paramagnéticos, ferrimagnéticos y antiferromagnéticos tienen diferentes estructuras de momentos magnéticos intrínsecos. A la temperatura de Curie específica de un material ( $T C$ ), estas propiedades cambian. La transición de antiferromagnético a paramagnético (o viceversa) ocurre a la temperatura de Néel ( $T N$ ), que es análoga a la temperatura de Curie.

A continuación $T C$	Arriba $T C$
Ferromagnetic	↔
Ferrimagnetic	↔
A continuación $T N$	Arriba $T N$
Antiferromagnetic	↔

Orientación de momentos magnéticos en materiales
Ferromagnetismo: Los momentos magnéticos en un material ferromagnético se ordenan y de la misma magnitud en ausencia de un campo magnético aplicado.
Paramagnetismo: Los momentos magnéticos en un material paramagnético están desordenados en ausencia de un campo magnético aplicado y ordenado en presencia de un campo magnético aplicado.
Ferrimagnetismo: Los momentos magnéticos en un material ferrimagnetico tienen diferentes magnitudes (debido al cristal que contienen dos tipos diferentes de iones magnéticos) que se alinean en contra de la ausencia de un campo magnético aplicado.
Antiferromagnetismo: Los momentos magnéticos en un material antiferromagnético tienen las mismas magnitudes pero están alineados en contra de la ausencia de un campo magnético aplicado.

Materiales con momentos magnéticos que cambian de propiedades a la temperatura de Curie

Las estructuras ferromagnéticas, paramagnéticas, ferrimagnéticas y antiferromagnéticas están formadas por momentos magnéticos intrínsecos. Si todos los electrones dentro de la estructura están emparejados, estos momentos se cancelan debido a sus giros opuestos y momentos angulares. Por lo tanto, incluso con un campo magnético aplicado, estos materiales tienen diferentes propiedades y no tienen temperatura de Curie.

Paramagnética

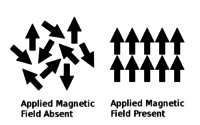
(feminine)

Un material es paramagnético solo por encima de su temperatura de Curie. Los materiales paramagnéticos son no magnéticos cuando no hay un campo magnético y magnéticos cuando se aplica un campo magnético. Cuando un campo magnético está ausente, el material tiene momentos magnéticos desordenados; es decir, los momentos magnéticos son asimétricos y no alineados. Cuando está presente un campo magnético, los momentos magnéticos se realinean temporalmente en paralelo al campo aplicado; los momentos magnéticos son simétricos y alineados. Los momentos magnéticos alineados en la misma dirección son los que causan un campo magnético inducido.

Para el paramagnetismo, esta respuesta a un campo magnético aplicado es positiva y se conoce como susceptibilidad magnética. La susceptibilidad magnética solo se aplica por encima de la temperatura de Curie para estados desordenados.

Las fuentes de paramagnetismo (materiales que tienen temperaturas de Curie) incluyen:

Todos los átomos que tienen electrones no deseados;
Los átomos que tienen cáscaras internas incompletas en electrones;
Los radicales libres;
Metales.

Por encima de la temperatura de Curie, los átomos se excitan y las orientaciones de espín se vuelven aleatorias, pero se pueden realinear mediante un campo aplicado, es decir, el material se vuelve paramagnético. Por debajo de la temperatura de Curie, la estructura intrínseca ha sufrido una transición de fase, los átomos están ordenados y el material es ferromagnético. Los materiales paramagnéticos' los campos magnéticos inducidos son muy débiles en comparación con los materiales ferromagnéticos & # 39; campos magnéticos.

Ferromagnético

Los materiales son solo ferromagnéticos por debajo de sus correspondientes temperaturas de Curie. Los materiales ferromagnéticos son magnéticos en ausencia de un campo magnético aplicado.

Cuando no hay un campo magnético, el material tiene una magnetización espontánea que es el resultado de los momentos magnéticos ordenados; es decir, para el ferromagnetismo, los átomos son simétricos y alineados en la misma dirección creando un campo magnético permanente.

Las interacciones magnéticas se mantienen unidas por interacciones de intercambio; de lo contrario, el desorden térmico superaría las débiles interacciones de los momentos magnéticos. La interacción de intercambio tiene una probabilidad cero de que los electrones paralelos ocupen el mismo punto en el tiempo, lo que implica una alineación paralela preferida en el material. El factor de Boltzmann contribuye en gran medida, ya que prefiere que las partículas que interactúan estén alineadas en la misma dirección. Esto hace que los ferroimanes tengan fuertes campos magnéticos y altas temperaturas de Curie de alrededor de 1000 K (730 °C).

Por debajo de la temperatura de Curie, los átomos están alineados y paralelos, provocando un magnetismo espontáneo; el material es ferromagnético. Por encima de la temperatura de Curie, el material es paramagnético, ya que los átomos pierden sus momentos magnéticos ordenados cuando el material sufre una transición de fase.

Ferrimagnético

Los materiales solo son ferrimagnéticos por debajo de su temperatura de Curie correspondiente. Los materiales ferrimagnéticos son magnéticos en ausencia de un campo magnético aplicado y están formados por dos iones diferentes.

Cuando no hay campo magnético, el material tiene un magnetismo espontáneo que es el resultado de momentos magnéticos ordenados; es decir, para el ferrimagnetismo, los momentos magnéticos de un ion están alineados mirando en una dirección con cierta magnitud y los momentos magnéticos del otro ion están alineados mirando en la dirección opuesta con una magnitud diferente. Como los momentos magnéticos son de diferentes magnitudes en direcciones opuestas, todavía hay un magnetismo espontáneo y un campo magnético está presente.

Al igual que los materiales ferromagnéticos, las interacciones magnéticas se mantienen unidas por interacciones de intercambio. Sin embargo, las orientaciones de los momentos son antiparalelas, lo que da como resultado un impulso neto al restar su impulso entre sí.

Por debajo de la temperatura de Curie los átomos de cada ion se alinean en forma antiparalela con diferentes momentos provocando un magnetismo espontáneo; el material es ferrimagnético. Por encima de la temperatura de Curie, el material es paramagnético ya que los átomos pierden sus momentos magnéticos ordenados cuando el material experimenta una transición de fase.

Antiferromagnético y la temperatura de Néel

Los materiales solo son antiferromagnéticos por debajo de su correspondiente temperatura de Néel o temperatura de pedido magnético, T_N. Esto es similar a la temperatura de Curie, ya que por encima de la temperatura de Néel, el material sufre una transición de fase y se vuelve paramagnético. Es decir, la energía térmica se vuelve lo suficientemente grande como para destruir el ordenamiento magnético microscópico dentro del material. Lleva el nombre de Louis Néel (1904-2000), quien recibió el Premio Nobel de Física en 1970 por su trabajo en el área.

El material tiene momentos magnéticos iguales alineados en direcciones opuestas, lo que da como resultado un momento magnético cero y un magnetismo neto de cero en todas las temperaturas por debajo de la temperatura de Néel. Los materiales antiferromagnéticos son débilmente magnéticos en ausencia o presencia de un campo magnético aplicado.

Al igual que los materiales ferromagnéticos, las interacciones magnéticas se mantienen unidas mediante interacciones de intercambio que evitan que el desorden térmico supere las interacciones débiles de los momentos magnéticos. Cuando se produce el desorden es a la temperatura de Néel.

A continuación se enumeran las temperaturas Néel de varios materiales:

Sustancia	Temperatura Néel (K)
MnO	116
MnS	160
MnTe	307
MnF2	67
FeF2	79
FeCl2	24
FeI2	9
Feo	198
FeOCl	80
CrCl2	25
CrI2	12
CoO	291
NiCl2	50
NiI2	75
NiO	525
KFeO₂	983
Cr	308
Cr2O3	307
Nd₅Ge₃	50

Ley de Curie-Weiss

La ley de Curie-Weiss es una versión adaptada de la ley de Curie.

La ley de Curie-Weiss es un modelo simple derivado de una aproximación de campo medio, lo que significa que funciona bien para la temperatura de los materiales, $T$ , mucho mayor que su correspondiente temperatura de Curie, $T C$ , es decir, $T ≫ T C$ ; sin embargo, no describe la susceptibilidad magnética, $χ$ , en las inmediaciones del punto de Curie debido a las fluctuaciones locales entre los átomos.

Ni la ley de Curie ni la ley de Curie-Weiss se cumplen para $T < T C$ .

Ley de Curie para un material paramagnético:

chi ={frac {M}{H}}={frac {Mmu _{0}}{B}}={frac {C}{T}}

Definición
$χ$	la susceptibilidad magnética; la influencia de un campo magnético aplicado en un material
$M$	los momentos magnéticos por volumen de unidad
$H$	el campo magnético macroscópico
$B$	el campo magnético
$C$	el material específico Curie constante

{displaystyle C={frac {mu _{0}mu _{mathrm {B} }^{2}}{3k_{mathrm {B} }}}N_{text{A}}g^{2}J(J+1)}

$N_{{text{A}}}$	la constante Avogadro
$μ 0$	la permeabilidad del espacio libre. Nota: en unidades CGS se toma a igual.
$g$	Landé g-factor
$J () J + 1)$	eigenvalue for eigenstate J² para los estados estacionarios dentro de las cáscaras de átomos incompletos (electros sin pagar)
$μ B$	el imán Bohr
$k B$	la constante Boltzmann
magnetismo total	es $N$ número de momentos magnéticos por volumen de unidad

La ley de Curie-Weiss se deriva entonces de la ley de Curie para ser:

{displaystyle chi ={frac {C}{T-T_{mathrm {C} }}}}

donde:

{displaystyle T_{mathrm {C} }={frac {Clambda }{mu _{0}}}}

$λ$ es la constante de campo molecular de Weiss.

Para conocer la derivación completa, consulte la ley de Curie-Weiss.

Física

Aproximación a la temperatura de Curie desde arriba

Como la ley de Curie-Weiss es una aproximación, se necesita un modelo más preciso cuando la temperatura, $T$ , se aproxima a la temperatura de Curie del material, $T C$ .

La susceptibilidad magnética se produce por encima de la temperatura de Curie.

Un modelo preciso de comportamiento crítico para la susceptibilidad magnética con exponente crítico $γ$ :

{displaystyle chi sim {frac {1}{(T-T_{mathrm {C} })^{gamma }}}}

El exponente crítico difiere entre materiales y para el modelo de campo medio se toma como $γ$ = 1.

Como la temperatura es inversamente proporcional a la susceptibilidad magnética, cuando $T$ se acerca a $T C$ el denominador tiende a cero y la susceptibilidad magnética se acerca al infinito permitiendo que ocurra el magnetismo. Este es un magnetismo espontáneo que es una propiedad de los materiales ferromagnéticos y ferrimagnéticos.

Aproximación a la temperatura de Curie desde abajo

El magnetismo depende de la temperatura y el magnetismo espontáneo se produce por debajo de la temperatura de Curie. Un modelo preciso de comportamiento crítico para el magnetismo espontáneo con exponente crítico $β$ :

{displaystyle Msim (T_{mathrm {C} }-T)^{beta }}

El exponente crítico difiere entre materiales y para el modelo de campo medio tomado como $β$ = 1/2 donde $T ≪ T C$ .

El magnetismo espontáneo se aproxima a cero a medida que la temperatura aumenta hacia la temperatura de Curie del material.

Acercándose al cero absoluto (0 kelvin)

El magnetismo espontáneo, que se produce en los materiales ferromagnéticos, ferrimagnéticos y antiferromagnéticos, se acerca a cero a medida que la temperatura aumenta hacia la temperatura de Curie del material. El magnetismo espontáneo alcanza su máximo cuando la temperatura se acerca a 0 K. Es decir, los momentos magnéticos están completamente alineados y en su mayor magnitud de magnetismo debido a la falta de perturbación térmica.

En los materiales paramagnéticos la energía térmica es suficiente para superar las alineaciones ordenadas. A medida que la temperatura se acerca a 0 K, la entropía disminuye a cero, es decir, el desorden disminuye y el material se ordena. Esto ocurre sin la presencia de un campo magnético aplicado y obedece a la tercera ley de la termodinámica.

Tanto la ley de Curie como la ley de Curie-Weiss fallan cuando la temperatura se acerca a 0 K. Esto se debe a que dependen de la susceptibilidad magnética, que solo se aplica cuando el estado está desordenado.

El sulfato de gadolinio continúa satisfaciendo la ley de Curie a 1 K. Entre 0 y 1 K, la ley no se cumple y se produce un cambio repentino en la estructura intrínseca a la temperatura de Curie.

Modelo de Ising de transiciones de fase

El modelo de Ising tiene una base matemática y puede analizar los puntos críticos de las transiciones de fase en orden ferromagnético debido a espines de electrones con magnitudes de ±1/2. Los espines interactúan con sus electrones dipolares vecinos en la estructura y aquí el modelo de Ising puede predecir su comportamiento entre sí.

Este modelo es importante para resolver y comprender los conceptos de transiciones de fase y, por lo tanto, resolver la temperatura de Curie. Como resultado, se pueden analizar muchas dependencias diferentes que afectan a la temperatura de Curie.

Por ejemplo, las propiedades de la superficie y del volumen dependen de la alineación y la magnitud de los giros y el modelo de Ising puede determinar los efectos del magnetismo en este sistema.

Debe tenerse en cuenta que, en 1D, la temperatura de Curie (crítica) para una transición de fase de orden magnético se encuentra a temperatura cero, es decir, el orden magnético toma el control solo en T = 0. En 2D, la temperatura crítica, p. una magnetización finita, se puede calcular resolviendo la desigualdad:

0.}" xmlns="http://www.w3.org/1998/Math/MathML">M=()1− − pecado− − 4⁡ ⁡ ()2β β J))1/8■0.{displaystyle M=(1-sinh ^{-4}(2beta J))}{1/8}]0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e9a483794a98d1353f532129ac9024bf0a6eb102" style="vertical-align: -0.838ex; width:31.215ex; height:3.343ex;"/>

Dominios de Weiss y temperaturas de Curie de superficie y volumen

Gráfico 3 Los dominios de Weiss en un material ferromagnético; los momentos magnéticos están alineados en dominios.

Las estructuras de los materiales consisten en momentos magnéticos intrínsecos que se separan en dominios denominados dominios de Weiss. Esto puede dar como resultado que los materiales ferromagnéticos no tengan magnetismo espontáneo, ya que los dominios podrían equilibrarse entre sí. Por lo tanto, la posición de las partículas puede tener diferentes orientaciones alrededor de la superficie que la parte principal (bulto) del material. Esta propiedad afecta directamente a la temperatura de Curie, ya que puede haber una temperatura de Curie general $T B$ y una temperatura de Curie superficial diferente $T S$ para un material.

Esto permite que la temperatura de Curie de la superficie sea ferromagnética por encima de la temperatura de Curie general cuando el estado principal está desordenado, es decir, los estados ordenados y desordenados ocurren simultáneamente.

Las propiedades de la superficie y del volumen se pueden predecir mediante el modelo de Ising y la espectroscopia de captura de electrones se puede utilizar para detectar los espines de los electrones y, por lo tanto, los momentos magnéticos en la superficie del material. Se toma un magnetismo total promedio de las temperaturas del volumen y de la superficie para calcular la temperatura de Curie del material, teniendo en cuenta que el volumen contribuye más.

El momento angular de un electrón es + $ħ$ /2 o − $ħ$ /2 debido a que tiene un giro de 1/2, que da un tamaño específico del momento magnético al electrón; el magnetón de Bohr. Los electrones que orbitan alrededor del núcleo en un bucle de corriente crean un campo magnético que depende del magnetón de Bohr y del número cuántico magnético. Por lo tanto, los momentos magnéticos están relacionados entre el momento angular y el orbital y se afectan entre sí. El momento angular contribuye dos veces más a los momentos magnéticos que el orbital.

Para el terbio, que es un metal de tierras raras y tiene un momento angular orbital alto, el momento magnético es lo suficientemente fuerte como para afectar el orden por encima de sus temperaturas generales. Se dice que tiene una gran anisotropía en la superficie, es decir, está muy dirigida en una orientación. Permanece ferromagnético en su superficie por encima de su temperatura de Curie (219K) mientras que su volumen se vuelve antiferromagnético y luego, a temperaturas más altas, su superficie permanece antiferromagnética por encima de su temperatura de Néel (230K) antes de volverse completamente desordenado y paramagnético al aumentar la temperatura. La anisotropía en masa es diferente de su anisotropía de superficie justo por encima de estos cambios de fase, ya que los momentos magnéticos se ordenarán de manera diferente o se ordenarán en materiales paramagnéticos.

Cambiar la temperatura de Curie de un material

Materiales compuestos

Los materiales compuestos, es decir, materiales compuestos de otros materiales con propiedades diferentes, pueden cambiar la temperatura de Curie. Por ejemplo, un compuesto que contiene plata puede crear espacios para las moléculas de oxígeno en el enlace, lo que disminuye la temperatura de Curie ya que la red cristalina no será tan compacta.

La alineación de los momentos magnéticos en el material compuesto afecta la temperatura de Curie. Si los momentos de los materiales son paralelos entre sí, la temperatura de Curie aumentará y, si son perpendiculares, la temperatura de Curie disminuirá, ya que se necesitará más o menos energía térmica para destruir las alineaciones.

La preparación de materiales compuestos a diferentes temperaturas puede dar como resultado diferentes composiciones finales que tendrán diferentes temperaturas de Curie. Dopar un material también puede afectar su temperatura de Curie.

La densidad de los materiales nanocompuestos cambia la temperatura de Curie. Los nanocompuestos son estructuras compactas a escala nanométrica. La estructura se construye a partir de temperaturas de Curie a granel altas y bajas; sin embargo, solo tendrá una temperatura de Curie de campo medio. Una densidad más alta de temperaturas de volumen más bajas da como resultado una temperatura de Curie de campo medio más baja y una densidad más alta de temperatura de campo más alta aumenta significativamente la temperatura de Curie de campo medio. En más de una dimensión la temperatura de Curie comienza a aumentar ya que los momentos magnéticos necesitarán más energía térmica para superar la estructura ordenada.

Tamaño de partícula

El tamaño de las partículas en la red cristalina de un material cambia la temperatura de Curie. Debido al pequeño tamaño de las partículas (nanopartículas), las fluctuaciones de los espines de los electrones se vuelven más prominentes, lo que hace que la temperatura de Curie disminuya drásticamente cuando el tamaño de las partículas disminuye, ya que las fluctuaciones causan desorden. El tamaño de una partícula también afecta la anisotropía, lo que hace que la alineación se vuelva menos estable y, por lo tanto, provoque desorden en los momentos magnéticos.

El extremo de esto es el superparamagnetismo que solo ocurre en pequeñas partículas ferromagnéticas. En este fenómeno, las fluctuaciones son muy influyentes, lo que hace que los momentos magnéticos cambien de dirección al azar y generen desorden.

La temperatura de Curie de las nanopartículas también se ve afectada por la estructura de la red cristalina: cúbica centrada en el cuerpo (bcc), cúbica centrada en la cara (fcc) y una estructura hexagonal (hcp) tienen diferentes temperaturas de Curie debido a los momentos magnéticos que reaccionan a sus electrones vecinos giran. fcc y hcp tienen estructuras más estrechas y, como resultado, tienen temperaturas de Curie más altas que bcc, ya que los momentos magnéticos tienen efectos más fuertes cuando están más cerca. Esto se conoce como el número de coordinación, que es el número de partículas vecinas más cercanas en una estructura. Esto indica un número de coordinación más bajo en la superficie de un material que en la masa, lo que hace que la superficie se vuelva menos significativa cuando la temperatura se acerca a la temperatura de Curie. En sistemas más pequeños, el número de coordinación de la superficie es más significativo y los momentos magnéticos tienen un efecto más fuerte en el sistema.

Aunque las fluctuaciones en las partículas pueden ser minúsculas, dependen en gran medida de la estructura de las redes cristalinas, ya que reaccionan con las partículas vecinas más cercanas. Las fluctuaciones también se ven afectadas por la interacción de intercambio, ya que se favorecen los momentos magnéticos paralelos y, por lo tanto, tienen menos perturbaciones y desorden, por lo tanto, una estructura más compacta influye en un magnetismo más fuerte y, por lo tanto, en una temperatura de Curie más alta.

Presión

La presión cambia la temperatura de Curie de un material. El aumento de la presión sobre la red cristalina disminuye el volumen del sistema. La presión afecta directamente la energía cinética de las partículas a medida que aumenta el movimiento, lo que hace que las vibraciones interrumpan el orden de los momentos magnéticos. Esto es similar a la temperatura ya que también aumenta la energía cinética de las partículas y destruye el orden de los momentos magnéticos y el magnetismo.

La presión también afecta la densidad de estados (DOS). Aquí, el DOS disminuye, lo que hace que disminuya la cantidad de electrones disponibles para el sistema. Esto lleva a que el número de momentos magnéticos disminuya, ya que dependen de los espines de los electrones. Se esperaría por esto que la temperatura de Curie disminuyera; sin embargo, aumenta. Este es el resultado de la interacción de intercambio. La interacción de intercambio favorece los momentos magnéticos paralelos alineados debido a que los electrones no pueden ocupar el mismo espacio en el tiempo y a medida que este aumenta debido a la disminución del volumen, la temperatura de Curie aumenta con la presión. La temperatura de Curie se compone de una combinación de dependencias de la energía cinética y el DOS.

La concentración de partículas también afecta la temperatura de Curie cuando se aplica presión y puede resultar en una disminución de la temperatura de Curie cuando la concentración está por encima de cierto porcentaje.

Ordenación de orbitales

El orden orbital cambia la temperatura de Curie de un material. El orden orbital se puede controlar mediante tensiones aplicadas. Esta es una función que determina la onda de un solo electrón o pares de electrones dentro del material. Tener control sobre la probabilidad de dónde estará el electrón permite alterar la temperatura de Curie. Por ejemplo, los electrones deslocalizados se pueden mover al mismo plano mediante tensiones aplicadas dentro de la red cristalina.

Se ve que la temperatura de Curie aumenta considerablemente debido a que los electrones se agrupan en el mismo plano, se ven obligados a alinearse debido a la interacción de intercambio y, por lo tanto, aumenta la fuerza de los momentos magnéticos, lo que evita el desorden térmico a temperaturas más bajas.

Temperatura de Curie en materiales ferroeléctricos

En analogía con los materiales ferromagnéticos y paramagnéticos, el término temperatura de Curie ( $T C$ ) también se aplica al temperatura a la que un material ferroeléctrico pasa a ser paraeléctrico. Por lo tanto, $T C$ es la temperatura a la que los materiales ferroeléctricos pierden su polarización espontánea cuando se produce un cambio de fase de primer o segundo orden. En caso de una transición de segundo orden, la temperatura de Curie Weiss $T 0$ que define el máximo de la constante dieléctrica es igual a la temperatura de Curie. Sin embargo, la temperatura de Curie puede ser 10 K mayor que $T 0$ en el caso de una transición de primer orden.

Gráfico 4 (Más despacio)

T 0

) polarización ferroeléctrica

P

en un campo eléctrico aplicado

E

Gráfico 5 (Ambove)

T 0

) polarización eléctrica

P

en un campo eléctrico aplicado

E

A continuación $T C$	Arriba $T C$
Ferroelectric	↔ Dielectric (paraelectric)
Antiferroelectric	↔ Dielectric (paraelectric)
Ferrielectric	↔ Dielectric (paraelectric)
Helielectric	↔ Dielectric (paraelectric)

Ferroeléctricos y dieléctricos

Los materiales son solo ferroeléctricos por debajo de su temperatura de transición correspondiente $T 0$ . Los materiales ferroeléctricos son todos piroeléctricos y por lo tanto tienen una polarización eléctrica espontánea ya que las estructuras son asimétricas.

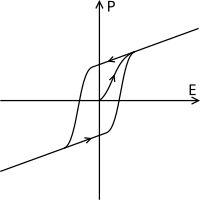
Materiales ferroeléctricos' la polarización está sujeta a histéresis (Figura 4); es decir, dependen tanto de su estado pasado como de su estado actual. A medida que se aplica un campo eléctrico, los dipolos se ven obligados a alinearse y se crea polarización; cuando se elimina el campo eléctrico, la polarización permanece. El bucle de histéresis depende de la temperatura y, como resultado, a medida que la temperatura aumenta y alcanza $T 0$ , las dos curvas se vuelven una. curva como se muestra en la polarización dieléctrica (Figura 5).

Permisividad relativa

Una versión modificada de la ley de Curie-Weiss se aplica a la constante dieléctrica, también conocida como permitividad relativa:

{displaystyle epsilon =epsilon _{0}+{frac {C}{T-T_{mathrm {0} }}}.}

Aplicaciones

Se utiliza una transición ferromagnética-paramagnética inducida por calor en medios de almacenamiento magnetoópticos para borrar y escribir nuevos datos. Los ejemplos famosos incluyen el formato Minidisc de Sony, así como el formato CD-MO ahora obsoleto. Se han propuesto y probado electroimanes de punto de Curie para mecanismos de actuación en sistemas de seguridad pasiva de reactores reproductores rápidos, donde las barras de control se dejan caer en el núcleo del reactor si el mecanismo de actuación se calienta más allá del punto de Curie del material. Otros usos incluyen el control de temperatura en soldadores y la estabilización del campo magnético de los generadores de tacómetro contra la variación de temperatura.

Contenido relacionado

Más resultados...