Temperamento igual
Un temperamento igual es un temperamento musical o sistema de afinación, que se aproxima a intervalos justos dividiendo una octava (u otro intervalo) en pasos iguales. Esto significa que la proporción de las frecuencias de cualquier par de notas adyacentes es la misma, lo que da un tamaño de paso percibido igual ya que el tono se percibe aproximadamente como el logaritmo de la frecuencia.
En la música clásica y la música occidental en general, el sistema de afinación más común desde el siglo XVIII ha sido el temperamento igual de doce tonos (también conocido como temperamento igual de 12 tonos, 12-TET o 12-ET; informalmente abreviado como doce iguales), que divide la octava en 12 partes, todas las cuales son iguales en una escala logarítmica, con una proporción igual a la raíz 12 de 2 (12 √2 ≈ 1.05946). Ese intervalo más pequeño resultante, 1⁄12 el anchura de una octava, se denomina semitono o semitono. En los países occidentales, el término temperamento igual, sin calificación, generalmente significa 12-TET.
En los tiempos modernos, 12-TET generalmente se afina en relación con un tono estándar de 440 Hz, llamado A440, lo que significa que una nota, A, se afina a 440 hercios y todas las demás notas se definen como un múltiplo de semitonos aparte de ella., ya sea de mayor o menor frecuencia. Sin embargo, el tono estándar no siempre ha sido 440 Hz; ha variado considerablemente y generalmente ha aumentado en los últimos cientos de años.
Otros temperamentos iguales dividen la octava de manera diferente. Por ejemplo, alguna música ha sido escrita en 19-TET y 31-TET, mientras que el sistema de tonos árabe usa 24-TET.
En lugar de dividir una octava, un temperamento igual también puede dividir un intervalo diferente, como la versión de temperamento igual de la escala Bohlen-Pierce, que divide el intervalo justo de una octava y una quinta (proporción 3:1), llamado "tritave" o una "pseudo-octava" en ese sistema, en 13 partes iguales.
Para los sistemas de afinación que dividen la octava por igual, pero que no son aproximaciones de solo intervalos, se puede usar el término división igual de la octava o EDO.
Los conjuntos de cuerdas sin trastes, que pueden ajustar la afinación de todas las notas excepto las cuerdas al aire, y los grupos vocales, que no tienen limitaciones mecánicas de afinación, a veces usan una afinación mucho más cercana a la entonación por razones acústicas. Otros instrumentos, como algunos instrumentos de viento, teclado y trastes, a menudo solo se aproximan al mismo temperamento, donde las limitaciones técnicas impiden afinaciones exactas. Algunos instrumentos de viento que pueden doblar su tono de manera fácil y espontánea, sobre todo los trombones, usan una afinación similar a los conjuntos de cuerdas y los grupos vocales.
Propiedades generales
En un temperamento igual, la distancia entre dos pasos adyacentes de la escala es el mismo intervalo. Debido a que la identidad percibida de un intervalo depende de su razón, esta escala en pasos pares es una secuencia geométrica de multiplicaciones. (Una secuencia aritmética de intervalos no sonaría espaciados uniformemente y no permitiría la transposición a diferentes tonos). Específicamente, el intervalo más pequeño en una escala de temperamento igual es la proporción:
donde la relación r divide la relación p (normalmente la octava, que es 2:1) en n partes iguales. (Ver Temperamento igual de doce tonos a continuación.)
Las escalas a menudo se miden en centavos, que dividen la octava en 1200 intervalos iguales (cada uno llamado centavo). Esta escala logarítmica hace que la comparación de diferentes sistemas de afinación sea más fácil que la comparación de proporciones y tiene un uso considerable en etnomusicología. El paso básico en centésimas para cualquier temperamento igual se puede encontrar tomando el ancho de p arriba en centésimas (generalmente la octava, que tiene 1200 centésimas de ancho), llamado debajo w, y dividiéndola en n partes:
En el análisis musical, el material que pertenece a un temperamento igual a menudo recibe una notación de número entero, lo que significa que se usa un solo número entero para representar cada tono. Esto simplifica y generaliza la discusión del material de tono dentro del temperamento de la misma manera que tomar el logaritmo de una multiplicación lo reduce a una suma. Además, al aplicar la aritmética modular donde el módulo es el número de divisiones de octava (generalmente 12), estos números enteros pueden reducirse a clases de tonos, lo que elimina la distinción (o reconoce la similitud) entre tonos del mismo nombre, p. c es 0 independientemente del registro de octava. El estándar de codificación MIDI utiliza designaciones de notas enteras.
Fórmulas generales para el intervalo de temperamento igual
Temperamento igual de doce tonos
El temperamento igual de 12 tonos, que divide la octava en doce intervalos del mismo tamaño, es el sistema musical más común que se usa en la actualidad, especialmente en la música occidental.
Historia
Las dos figuras a las que con frecuencia se les atribuye el logro del cálculo exacto del temperamento igual son Zhu Zaiyu (también romanizado como Chu-Tsaiyu. Chino: 朱 載堉) en 1584 y Simon Stevin en 1585. Según Fritz A. Kuttner, un crítico de la teoría, se sabe que "Chu-Tsaiyu presentó una muy precisa, simple y ingenioso método para el cálculo aritmético de monocordes de temperamento igual en 1584" y que "Simon Stevin ofreció una definición matemática de temperamento igual además de un cálculo algo menos preciso de los valores numéricos correspondientes en 1585 o después." Los desarrollos ocurrieron de forma independiente.
Kenneth Robinson atribuye la invención del temperamento igual a Zhu Zaiyu y proporciona citas textuales como evidencia. Se cita a Zhu Zaiyu diciendo que, en un texto que data de 1584, "He fundado un nuevo sistema". Establezco un pie como el número del que se han de sacar los otros, y usando proporciones los extraigo. En total, hay que encontrar las cifras exactas de los flautistas en doce operaciones." Kuttner no está de acuerdo y comenta que su afirmación 'no puede considerarse correcta sin mayores calificaciones'. Kuttner propone que ni Zhu Zaiyu ni Simon Stevin alcanzaron el mismo temperamento y que ninguno de los dos debería ser tratado como inventor.
China
Mientras que China había presentado previamente aproximaciones para 12-TET, Zhu Zaiyu fue la primera persona en resolver matemáticamente el temperamento igual de doce tonos, que describió en su Fusión de música y calendario (< span title="Texto en idioma chino">律暦融通) en 1580 y Compendio completo de música y tono ( Yuelü quan shu 樂律全書) en 1584. Joseph Needham también da un relato extenso. Zhu obtuvo su resultado matemáticamente dividiendo la longitud de la cuerda y la tubería sucesivamente por 12 √2 ≈ 1.059463, y para longitud de tubería por 24√2< /span>, tal que después de doce divisiones (una octava) la longitud se dividió por un factor de 2.
Zhu Zaiyu creó varios instrumentos adaptados a su sistema, incluidas las pipas de bambú.
Europa
Algunos de los primeros europeos en abogar por el temperamento igualitario fueron los laudistas Vincenzo Galilei, Giacomo Gorzanis y Francesco Spinacino, quienes escribieron música en él.
Simon Stevin fue el primero en desarrollar 12-TET basado en la raíz doceava de dos, que describió en Van De Spiegheling der singconst (ca. 1605), publicado póstumamente casi tres siglos después en 1884.
Los músicos de instrumentos de cuerda pulsada (laudistas y guitarristas) generalmente favorecían el temperamento igualitario, mientras que otros estaban más divididos. Al final, ganó el temperamento igual de doce tonos. Esto permitió que se desarrollaran y florecieran la modulación enarmónica, nuevos estilos de tonalidad simétrica y politonalidad, música atonal como la escrita con la técnica dodecafónica o el serialismo, y el jazz (al menos su componente pianístico).
Matemáticas
En el temperamento igual de doce tonos, que divide la octava en 12 partes iguales, el ancho de un semitono, es decir, la relación de frecuencia del intervalo entre dos notas adyacentes, es la raíz doceava de dos:
Este intervalo se divide en 100 centavos.
Cálculo de frecuencias absolutas
Para encontrar la frecuencia, Pn, de una nota en 12-TET, se puede usar la siguiente definición:
En esta fórmula, Pn se refiere al tono o frecuencia (generalmente en hercios) que está tratando de encontrar. Pa se refiere a la frecuencia de un tono de referencia. n y a se refieren a los números asignados al tono deseado y al tono de referencia, respectivamente. Estos dos números son de una lista de enteros consecutivos asignados a semitonos consecutivos. Por ejemplo, A4 (el tono de referencia) es la tecla 49 desde el extremo izquierdo de un piano (afinado a 440 Hz), y C4 (C central), y F#4 son las teclas 40 y 46 respectivamente. Estos números se pueden usar para encontrar la frecuencia de C4 y F#4:
Conversión de frecuencias a sus equivalentes de igual temperamento
Para convertir una frecuencia (en Hz) a su contraparte igual de 12 TET, se puede usar la siguiente fórmula:
Donde En se refiere a la frecuencia de un tono en temperamento igual, y a se refiere a la frecuencia de un tono de referencia. Por ejemplo, (si dejamos que el tono de referencia sea igual a 440 Hz) podemos ver que E5 y C#5 son iguales a las siguientes frecuencias respectivamente:
Comparación con entonación justa
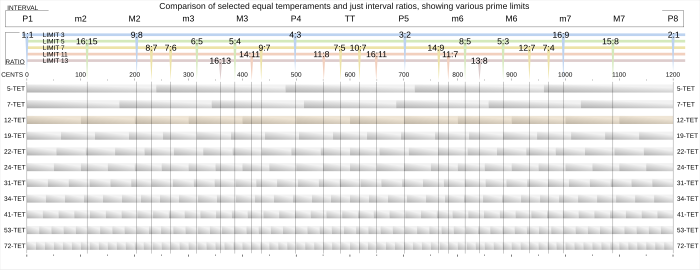
Los intervalos de 12-TET se aproximan mucho a algunos intervalos en entonación justa. Las quintas y las cuartas están casi indistinguiblemente cerca de los intervalos, mientras que las terceras y las sextas están más alejadas.
En la siguiente tabla, los tamaños de varios intervalos justos se comparan con sus contrapartes de igual temperamento, dados como una proporción y también como centavos.
| Interval Name | Valor real en 12-TET | Valor decimal en 12-TET | Cents | Sólo intervalo de intonación | Cientos en la intonación | Diferencia |
|---|---|---|---|---|---|---|
| Unison (C) | 20.12 = 1 | 1 | 0 | 1.1 = 1 | 0 | 0 |
| Menor segundo (D bebido) | 21.12 = 12√2 | 1.059463 | 100 | 16.15 = 1.06666... | 111.73 | -11.73 |
| Segundo mayor (D) | 22.12 = 6√2 | 1.122462 | 200 | 9.8 = 1.125 | 203.91 | -3.91 |
| Tercero menor (E bebe) | 23.12 = 4√2 | 1.189207 | 300 | 6.5 = 1.2 | 315.64 | -15.64 |
| Tercero mayor (S) | 24.12 = 3√2 | 1.259921 | 400 | 5.4 = 1,25 | 386.31 | +13.69 |
| Cuarto (F) perfecto | 25.12 = 12√32 | 1.33484 | 500 | 4.3 = 1.33333... | 498.04 | +1.96 |
| Tritone (G bebido) | 26.12 = √2 | 1.414214 | 600 | 64.45= 1.42222... | 609.78 | -9.78 |
| Quinto (G) perfecto | 27.12 = 12√128 | 1.498307 | 700 | 3.2 = 1,5 | 701.96 | -1.96 |
| Sexto menor (A bebe) | 28.12 = 3√4 | 1.587401 | 800 | 8.5 = 1.6 | 813.69 | -13.69 |
| Sexto mayor (A) | 29.12 = 4√8 | 1.681793 | 900 | 5.3 = 1.66666... | 884.36 | +15.64 |
| Menor séptimo (B bebido) | 210.12 = 6√32 | 1.781797 | 1000 | 16.9 = 1.77777... | 996.09 | +3.91 |
| Séptimo Mayor (B) | 211.12 = 12√2048 | 1.887749 | 1100 | 15.8= 1.875 | 1088.270 | +11.73 |
| Octave (C) | 212.12 = 2 | 2 | 1200 | 2.1 = 2 | 1200,00 | 0 |
División igual de siete tonos de la quinta
Los violines, las violas y los violonchelos se afinan en quintas perfectas (G – D – A – E, para violines, y C – G – D – A, para violas y violonchelos), lo que sugiere que su proporción de semitonos es ligeramente más alto que en el temperamento igual de doce tonos convencional. Debido a que una quinta perfecta está en una relación de 3:2 con su tono base, y este intervalo se cubre en 7 pasos, cada tono está en la proporción de 7√ 3⁄2 al siguiente (100,28 centavos), lo que proporciona una quinta perfecta con una proporción de 3:2 pero una octava ligeramente ampliada con una proporción de ≈ 517:258 o ≈ 2,00388:1 en lugar de la proporción habitual de 2:1, porque doce quintas perfectas no equivalen a siete octavas. Sin embargo, durante la ejecución real, el violinista elige los tonos de oído, y solo se garantiza que los cuatro tonos continuos de las cuerdas muestren esta proporción de 3:2.
Otros temperamentos iguales
Temperamentos de 5 y 7 tonos en etnomusicología
Cinco y siete tonos iguales de temperamento (5-TET ![]() Jugar(help·info) y 7-TET
Jugar(help·info) y 7-TET![]() Jugar(help·info)), con 240
Jugar(help·info)), con 240 ![]() Jugar(help·info) y 171
Jugar(help·info) y 171 ![]() Jugar(help·info) céntimo de pasos, respectivamente, son bastante comunes.
Jugar(help·info) céntimo de pasos, respectivamente, son bastante comunes.
5-TET y 7-TET marcan los puntos finales del rango de afinación válido del temperamento sintónico, como se muestra en la Figura 1.
- En 5-TET la quinta perfecta templada es de 720 centavos de ancho (en la parte superior del continuum de afinación), y marca el punto final en el continuum de afinación en el que el ancho del segundo menor se contrae a un ancho de 0 centavos.
- En 7-TET el quinto perfecto templado es de 686 céntimos de ancho (en la parte inferior de la continuum de afinación), y marca el punto final en el continuum de afinación, en el que el segundo menor se expande a ser tan ancho como el segundo mayor (en 171 centavos cada uno).
Temperamento igual de 5 tonos
Los gamelanes indonesios son sintonizados con 5-TET según Kunst (1949), pero según Hood (1966) y McPhee (1966) su afinación varía ampliamente, y según Tenzer (2000) contienen octavas estiradas. Ahora es bien aceptado que de los dos sistemas de afinación primaria en la música de gamelan, slendro y pelog, sólo el eslondro algo se asemeja al temperamento igual de cinco toneladas mientras que el pelog es altamente desigual; sin embargo, Surjodiningrat et al. (1972) ha analizado pelog como un subconjunto de siete notas de un temperamento igual de nueve toneladas (133 pasos-cento) ![]() Jugar(help·info)).
Jugar(help·info)).
Temperamento igual de 7 tonos
A xilófono tailandés medido por Morton (1974) "varió sólo más o menos 5 centavos", de 7-TET. Según Morton, "Los instrumentos tailandeses de campo fijo están afinados a un sistema equidistante de siete parcelas por octava... Como en la música tradicional occidental, sin embargo, todas las parcelas del sistema de afinación no se utilizan en un modo (a menudo denominado 'escala'); en el sistema tailandés cinco de los siete se utilizan en los principales lanzamientos en cualquier modo, estableciendo así un patrón de intervalos no equivalentes para el modo." ![]() Jugar(help·info)
Jugar(help·info)
Una escala de indios sudamericanos de una cultura preinstrumental medida por Boiles (1969) presentaba un temperamento igual de siete tonos de 175 centavos, que estira la octava ligeramente como con la música instrumental de gamelán.
La música china ha utilizado tradicionalmente 7-TET.
Varios temperamentos iguales
19 EDO es famoso y algunos instrumentos están afinados en 19 EDO. Tiene una quinta perfecta ligeramente más plana (a 695 centésimas), pero su sexta mayor está a menos de una centésima de distancia de la sexta mayor de la entonación justa (a 884 centésimas). Su tercera menor también está a menos de un centavo de la entonación justa. (El EDO más bajo que produce una mejor tercera menor y una sexta mayor que 19 EDO es 232 EDO). Su cuarta perfecta (a 505 centavos), tiene solo 5 centavos de sostenido que solo la entonación y 3 centavos de sostenido de 12 tet& #39;
23 EDO es el EDO más grande que no se aproxima a los armónicos 3, 5, 7 y 11 (3: 2, 5: 4, 7: 4, 11: 8) dentro de los 20 centavos, lo que lo hace atractivo para microtonalistas que buscan para territorio armónico microtonal inusual.
24 EDO, la escala de un cuarto de tono (o 24-TET), fue una afinación microtonal popular en el siglo XX, probablemente porque representaba un punto de acceso conveniente para los compositores condicionados por las prácticas estándar de notación y tono de 12 EDO occidentales que también estaban interesados en microtonalidad. Debido a que 24 EDO contiene todos los tonos de 12 EDO, más nuevos tonos a mitad de camino entre cada par adyacente de 12 tonos EDO, podrían emplear los colores adicionales sin perder ninguna de las tácticas disponibles en la armonía de 12 tonos. El hecho de que 24 sea un múltiplo de 12 también hizo que 24 EDO fuera fácil de lograr instrumentalmente mediante el empleo de dos instrumentos tradicionales de 12 EDO afinados deliberadamente con un cuarto de tono, como dos pianos, lo que también permitió que cada intérprete (o un intérprete tocando un piano diferente con cada mano) para leer la notación familiar de 12 tonos. Varios compositores, incluido Charles Ives, experimentaron con música para pianos de cuarto de tono. 24 EDO se aproxima muy bien al armónico 11, a diferencia de 12 EDO.
26 EDO es el EDO más pequeño para sintonizar casi exclusivamente el 7º armónico (7:4). También es un temperamento de tono medio muy plano, lo que significa que después de 4 quintas, produce una tercera neutra en lugar de una mayor. 26 EDO tiene dos terceras menores y dos sextas menores. Puede ser un poco confuso a primera vista porque si tocas la tercera neutra suena como una mayor muy plana. 26EDO podría ser un temperamento alternativo de armonía Barbershop.
27 EDO es el EDO más pequeño que representa de forma única todos los intervalos que involucran los primeros ocho armónicos. Templa la coma septimal pero no la coma sintónica.
29 EDO es el número más bajo de divisiones iguales de octava que produce una quinta perfecta mejor que 12 EDO. Su tercera mayor es aproximadamente tan inexacta como 12-TET; sin embargo, está afinado 14 centavos en lugar de 14 centavos sostenido. También afina los armónicos 7, 11 y 13 planos, aproximadamente en la misma cantidad. Esto significa que intervalos como 7:5, 11:7, 13:11, etc., se combinan extremadamente bien en 29-TET.
31 EDO fue defendido por Christiaan Huygens y Adriaan Fokker. 31 EDO tiene una quinta un poco menos precisa que 12 EDO, pero proporciona casi solo tercios mayores y proporciona coincidencias decentes para armónicos hasta al menos 13, de los cuales el séptimo armónico es particularmente preciso.
34 EDO da un poco menos de errores totales combinados de aproximación a las proporciones justas de 5 límites 3:2, 5:4, 6:5 y sus inversiones que 31 EDO, aunque la aproximación de 5:4 es peor. 34 EDO no se aproxima a las proporciones que involucran al pozo principal 7. Contiene un tritono de 600 centavos, ya que es un EDO par.
41 EDO es el segundo número más bajo de divisiones iguales que produce una quinta perfecta mejor que 12 EDO. Su tercera mayor es más precisa que 12 EDO y 29 EDO, aproximadamente 6 centavos planos. No significa tono, por lo que distingue 10:9 y 9:8, a diferencia de 31edo. Es más preciso en 13-limit que en 31edo.
46 EDO proporciona terceras mayores ligeramente agudas y quintas perfectas, dando a las tríadas un sonido brillante característico. Los armónicos hasta el 11 se aproximan con una precisión de 5 centésimas, estando 10:9 y 9:5 a una quinta parte de la pureza. Como no es un sistema de tono medio, distingue 10:9 y 9:8.
53 EDO es mejor para aproximarse a las consonancias justas tradicionales que 12, 19 o 31 EDO, pero solo ha tenido un uso ocasional. Sus quintas perfectas extremadamente buenas lo hacen intercambiable con una afinación pitagórica extendida, pero también se adapta al temperamento cismático y, a veces, se usa en la teoría de la música turca. Sin embargo, no se ajusta a los requisitos de los temperamentos de tono medio, que ponen buenas terceras al alcance de la mano a través del ciclo de quintas. En 53 EDO, las terceras consonantes se alcanzarían en su lugar usando una cuarta disminuida pitagórica (C-F♭), ya que es un ejemplo de temperamento cismático, al igual que 41 EDO.
72 EDO se aproxima bien a muchos intervalos de entonación justa, incluso en el límite de 7 y el límite de 11, como 7:4, 9:7, 11:5, 11:6 y 11:7. 72 EDO ha sido enseñado, escrito e interpretado en la práctica por Joe Maneri y sus alumnos (cuyas inclinaciones atonales suelen evitar cualquier referencia a la entonación justa). Puede considerarse una extensión de 12 EDO porque 72 es un múltiplo de 12. 72 EDO tiene un intervalo más pequeño que es seis veces más pequeño que el intervalo más pequeño de 12 EDO y, por lo tanto, contiene seis copias de 12 EDO que comienzan en tonos diferentes. También contiene tres copias de 24 EDO y dos copias de 36 EDO, que son a su vez múltiplos de 12 EDO. 72 EDO también ha sido criticado por su redundancia al retener las aproximaciones deficientes contenidas en 12 EDO, a pesar de no necesitarlas para ningún límite inferior de entonación justa (por ejemplo, 5-límite).
96 EDO se aproxima a todos los intervalos dentro de 6,25 centavos, que apenas se distingue. Como un múltiplo de ocho veces de 12, se puede usar completamente como el 12 EDO común. Ha sido propugnada por varios compositores, especialmente Julián Carrillo desde 1924 hasta la década de 1940.
Otras divisiones iguales de la octava que han encontrado uso ocasional incluyen 15 EDO, 17 EDO y 22 EDO.
2, 5, 12, 41, 53, 306, 665 y 15601 son denominadores de los primeros convergentes de log2(3), entonces 2, 5, 12, 41, 53, 306, 665 y 15601 doceavos (y quintos), siendo en correspondencia temperamentos iguales a un número entero de octavas, son una mejor aproximación de 2, 5, 12, 41, 53, 306, 665 y 15601 solo doceavos/quintos que para cualquier temperamento igual con menos tonos.
1, 2, 3, 5, 7, 12, 29, 41, 53, 200... (secuencia A060528 en el OEIS) es la secuencia de divisiones de octava que proporcionan cada vez mejores aproximaciones de la quinta justa. Las secuencias relacionadas contienen divisiones que se aproximan a otros intervalos justos.
temperamentos iguales de intervalos no octavas
(feminine)La versión igualada de la escala Bohlen-Pierce consiste en la relación 3:1, 1902 centavos, convencionalmente una quinta perfecta más una octava (es decir, un duodécimo perfecto), llamada en esta teoría un tritave (![]() Jugar(help·info)), y dividir en trece partes iguales. Esto proporciona un partido muy cercano a ratios ajustadas justamente que consiste sólo en números impares. Cada paso es de 146,3 centavos (
Jugar(help·info)), y dividir en trece partes iguales. Esto proporciona un partido muy cercano a ratios ajustadas justamente que consiste sólo en números impares. Cada paso es de 146,3 centavos (![]() Jugar(help·info)), o 13√3.
Jugar(help·info)), o 13√3.
Wendy Carlos creó tres temperamentos iguales inusuales después de un estudio exhaustivo de las propiedades de los posibles temperamentos que tienen un tamaño de paso entre 30 y 120 centavos. Estos fueron llamados alfa, beta y gamma. Se pueden considerar como divisiones iguales de la quinta perfecta. Cada uno de ellos proporciona una muy buena aproximación de varios intervalos justos. Sus tamaños de paso:
- alfa: 9√3.2 (78.0 centavos)
 Jugar(help·info)
Jugar(help·info) - beta: 11√3.2 (63,8%)
 Jugar(help·info)
Jugar(help·info) - gamma: 20√3.2 (35,1 centavos)
 Jugar(help·info)
Jugar(help·info)
Alpha y Beta se pueden escuchar en la canción principal de su álbum de 1986 Beauty in the Beast.
Proporciones entre semitono y tono completo
En esta sección, semitono y tono completo pueden no tener sus significados habituales de 12-EDO, ya que analiza cómo se pueden atenuar de formas diferentes a sus versiones justas. para producir las relaciones deseadas. Sea s el número de pasos en un semitono y t el número de pasos en un tono.
Existe exactamente una familia de temperamentos iguales que fija el semitono en cualquier fracción propia de un tono completo, mientras mantiene las notas en el orden correcto (lo que significa que, por ejemplo, C, D, E, F y F< span class="music-symbol" style="font-family: Arial Unicode MS, Lucida Sans Unicode;">♯ están en orden ascendente si conservan sus relaciones habituales con C). Es decir, fijando q a una fracción propia en la relación qt = s también define una familia única de un temperamento igual y sus múltiplos que cumplen esta relacion.
Por ejemplo, donde k es un número entero, 12k-EDO establece q = 1⁄2, y 19k-EDO establece q = 1⁄3. Los múltiplos más pequeños de estas familias (por ejemplo, 12 y 19 arriba) tienen la propiedad adicional de no tener notas fuera del círculo de quintas. (Esto no es cierto en general; en 24-EDO, los medios sostenidos y los medios bemoles no están en el círculo de quintas generado a partir de C). Los casos extremos son 5k-EDO, donde q = 0 y el semitono se convierte en unísono, y 7k-EDO, donde q = 1 y el semitono y el tono son iguales intervalo.
Una vez que uno sabe cuántos pasos tiene un semitono y un tono en este temperamento igual, puede encontrar el número de pasos que tiene en la octava. Un temperamento igual que cumpla con las propiedades anteriores (incluida la ausencia de notas fuera del círculo de quintas) divide la octava en pasos de 7t − 2s, y la quinta justa en 4< i>t − s pasos. Si hay notas fuera del círculo de quintas, entonces se deben multiplicar estos resultados por n, que es el número de círculos de quintas que no se superponen necesarios para generar todas las notas (por ejemplo, dos en 24-EDO, seis en 72-EDO). (Uno debe tomar el semitono pequeño para este propósito: 19-EDO tiene dos semitonos, uno de los cuales es 1⁄3 tono y el otro es 2⁄3.)
La más pequeña de estas familias es 12k-EDO y, en particular, 12-EDO es el temperamento igual más pequeño que tiene las propiedades anteriores. Además, también hace que el semitono sea exactamente medio tono entero, la relación más simple posible. Estas son algunas de las razones por las que 12-EDO se ha convertido en el temperamento igual más utilizado. (Otra razón es que 12-EDO es el temperamento igual más pequeño que se aproxima mucho a la armonía de 5 límites, siendo el siguiente más pequeño 19-EDO).
Cada elección de fracción q para la relación da como resultado exactamente una familia de temperamento igual, pero lo contrario no es cierto: 47-EDO tiene dos semitonos diferentes, donde uno es 1⁄7 tono y el otro es 8⁄9, que no son complementos entre sí como en 19-EDO (1⁄3 y 2⁄3). Tomar cada semitono da como resultado una elección diferente de quinta perfecta.
Sistemas de afinación relacionados
Afinaciones diatónicas regulares
La afinación diatónica en doce iguales se puede generalizar a cualquier afinación diatónica regular dividiendo la octava como una secuencia de pasos TTSTTTS (o una rotación de la misma) con todas las T's y todas las S's la misma talla y las S's más pequeñas que las T's. En doce iguales, la S es el semitono y tiene exactamente la mitad del tamaño del tono T. Cuando las S se reducen a cero, el resultado es TTTTT o un temperamento igual de cinco tonos. A medida que los semitonos se hacen más grandes, eventualmente los pasos son todos del mismo tamaño, y el resultado es un temperamento igual de siete tonos. Estos dos puntos finales no se incluyen como afinaciones diatónicas regulares.
Las notas en una afinación diatónica regular están conectadas entre sí por un ciclo de siete quintas templadas. El sistema de doce tonos se generaliza de manera similar a una secuencia CDCDDCDCDCDD (o una rotación de la misma) de semitonos cromáticos y diatónicos conectados entre sí en un ciclo de doce quintos. En este caso, siete iguales se obtienen en el límite cuando el tamaño de C tiende a cero y cinco iguales es el límite cuando D tiende a cero mientras que doce iguales es, por supuesto, el caso C = D.
Algunos de los tamaños intermedios de tonos y semitonos también se pueden generar en sistemas de temperamento igual. Por ejemplo, si el semitono diatónico es el doble del tamaño del semitono cromático, es decir, D = 2*C, el resultado es diecinueve iguales con un paso para el semitono cromático, dos pasos para el semitono diatónico y tres pasos para el tono y el número total. de pasos 5*T + 2*S = 15 + 4 = 19 pasos. El sistema de doce tonos resultante se aproxima mucho al históricamente importante 1/3 coma significado.
Si el semitono cromático es dos tercios del tamaño del semitono diatónico, es decir, C = (2/3)*D, el resultado es treinta y uno iguales, con dos pasos para el semitono cromático, tres pasos para el diatónico semitono y cinco pasos para el tono donde 5*T + 2*S = 25 + 6 = 31 pasos. El sistema de doce tonos resultante se aproxima mucho al históricamente importante medio tono de 1/4 de coma.
Contenido relacionado
Dinah washington
Clasificación de instrumentos musicales
Theremin


![{displaystyle r={sqrt[{n}]{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b55fb394d767c50fb569ca27fd636072c72fbd7c)



![{displaystyle {sqrt[{12}]{2}}=2^{frac {1}{12}}approx 1.059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232c2beab28b1c46c328080d982595d9ef196e08)
![{displaystyle P_{n}=P_{a}left({sqrt[{12}]{2}}right)^{(n-a)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
![{displaystyle P_{40}=440left({sqrt[{12}]{2}}right)^{(40-49)}approx 261.626 mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16dc9af5bbe778786f73eca304c80c72584cd70)
![{displaystyle P_{46}=440left({sqrt[{12}]{2}}right)^{(46-49)}approx 369.994 mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)





