Temperamento de tono medio
Meantone temperament es un temperamento musical, es decir, un sistema de afinación, que se obtiene estrechando las quintas para que su relación sea ligeramente inferior a 3:2 (haciéndolas más estrechas que una quinta perfecta), para acercar las terceras a la pureza. Los temperamentos de tono medio se construyen de la misma manera que la afinación pitagórica, como una pila de quintas iguales, pero es un temperamento en el que las quintas no son puras.
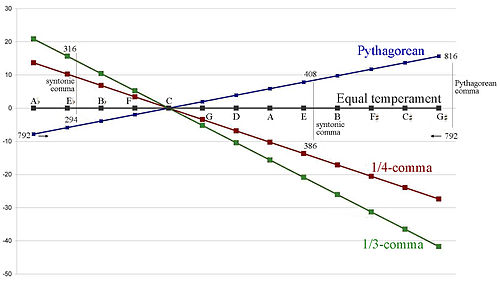
Temperamentos de tono medio notables
Temperamento igual, obtenido al hacer que todos los semitonos sean del mismo tamaño, cada uno igual a un doceavo de octava (con una proporción de la raíz 12 de 2 a uno (12√2:1), reduce las quintas en aproximadamente 2 centésimas o 1/12 de una coma pitagórica, y produce terceras que son solo ligeramente mejores que en la afinación pitagórica. El temperamento igual es aproximadamente lo mismo que la afinación de 1/11 de coma en significado de tono.
El mesotónico de un cuarto de coma, que atempera las quintas por 1/4 de una coma sintónica, es el tipo de temperamento de semitono más conocido, y el término temperamento de semitono se usa a menudo para referirse específicamente a él.. Cuatro quintas ascendentes (como C-G-D-A-E) templadas por 1/4 de coma producen una tercera mayor perfecta (C-E), una coma sintónica más estrecha que la tercera pitagórica que resultaría de cuatro quintas perfectas. El mediotono de un cuarto de coma se ha practicado desde principios del siglo XVI hasta finales del XIX. Se puede aproximar mediante una división de la octava en 31 pasos iguales.
En el significado de tercera coma, las quintas están atenuadas por 1/3 de coma, y tres quintas descendentes (como A–D–G–C) producen una tercera menor perfecta (A–C) una coma sintónica más ancha que la Pitagórico que resultaría de tres quintas perfectas. El significado de la tercera coma se puede aproximar extremadamente bien mediante una división de la octava en 19 pasos iguales.
El tono como medio
El nombre "temperamento de tono medio" deriva del hecho de que todos estos temperamentos tienen solo un tamaño de tono, mientras que la entonación simple produce un tono mayor y uno menor, que se diferencian por una coma sintónica. En cualquier sistema regular (es decir, con todas las quintas menos una del mismo tamaño) el tono (como C–D) se alcanza después de dos quintas (como C–G–D), mientras que el tercio mayor se alcanza después de cuatro quintas: el tono por lo tanto es exactamente la mitad de la tercera mayor.
Este es un sentido en el que el tono es un medio.
En el caso del significado de un cuarto de coma, además, donde la tercera mayor se estrecha con una coma sintónica, el tono también es media coma más estrecho que el tono mayor de entonación justa, o media coma más ancho que el tono menor: este es otro sentido en el que el tono en el temperamento de un cuarto de tono puede considerarse un tono medio, y explica por qué el tono medio de un cuarto de coma a menudo se considera el temperamento de tono medio propiamente dicho.
Temperamentos de tono medio
"Meantono" puede recibir las siguientes definiciones equivalentes:
- El pretendido es el medio geométrico entre el tono entero mayor (9:8 en la intonación justa) y el tono entero menor (10:9 en la intonación justa).
- El significado es la media de su tercera mayor (por ejemplo, la raíz cuadrada de 5:4 en el cuarto-comma signone).
La familia de temperamentos mesotónicos comparte la característica común de que forman una pila de quintas idénticas, siendo el tono completo (segunda mayor) el resultado de dos quintas menos una octava, la tercera mayor de cuatro quintas menos dos octavas. Los temperamentos de tono medio a menudo se describen por la fracción de la coma sintónica por la que se atemperan las quintas: el medio tono de un cuarto de coma, el tipo más común, atempera las quintas por 1⁄4 de una coma sintónica, con el resultado de que cuatro quintas producen una tercera mayor justa, una coma sintónica inferior a una tercera mayor pitagórica; temperamentos de medio tono de tercera coma por 1⁄3 de una coma sintónica, tres quintas que producen una sexta mayor (y por lo tanto una tercera menor), una coma sintónica más baja que una pitagórica.
Un temperamento de tono medio es un temperamento lineal, que se distingue por el ancho de su generador (el quinto, a menudo medido en centavos). Los temperamentos de tono medio históricamente notables, discutidos a continuación, ocupan una porción estrecha de este continuo de afinación, con quintas que van desde aproximadamente 695 a 699 centavos.
Los temperamentos de tono medio se pueden especificar de varias maneras: por qué fracción (logarítmicamente) de una coma sintónica se aplana la quinta (como se indicó anteriormente), qué temperamento igual tiene la quinta de tono medio en cuestión, el ancho de la quinta perfecta temperada en centésimas, o la relación entre el tono completo y el semitono diatónico. Esta última relación se denominó "R" por el compositor, pianista y teórico estadounidense Easley Blackwood, pero en efecto ha estado en uso por mucho más tiempo que eso. Es útil porque da una idea de las cualidades melódicas de la afinación y porque si R es un número racional N/D , también lo es 3R + 1/5R + 2 o 3N + D/5N + 2D, que es el tamaño de la quinta en términos de logaritmos en base 2, y que inmediatamente nos dice qué división de octava tendremos.
Si nos multiplicamos por 1200, tenemos el tamaño de quinto en centavos.
En estos términos, a continuación se enumeran algunas afinaciones de tono medio históricamente notables. La segunda y cuarta columna son aproximaciones correspondientes a la primera columna. La tercera columna muestra qué tan cerca está la aproximación de la segunda columna al tamaño real del quinto intervalo en la afinación de tono medio dada de la primera columna.
| Fracción de un (sintónico) coma | Intervalo puro | Tamaño aproximado de la quinta en octavas | Error (en centavos) | Ratio R | ET aproximado |
|---|---|---|---|---|---|
| 1.315 (Aproximadamente afinación pitagórica) | 3311× 5.2495, pero 3.2 puede considerarse puro para todos los fines prácticos (perfecto quinto, tono entero mayor) | 31.53 | +6.55227×10; 5 - | 9:4 | 53 |
| 1.11 ()1.12 Pythagorean comma) | 16384.10935 ()214.37× 5) (Kirnberger quinto, un perfecto quinto aplanado por un cisma) | 7.12 | +1.16371×10−4 | 2:1 | 12 |
| 1.6 | 45.32 y 64.45 (tritone) | 32.55 | -1.88801×10−1 | 9:5 | 55 |
| 1.5 | 15.8 y 16.15 (semitone diatónico) | 25.43 | +2.06757×10−2 | 7:4 | 43 |
| 1.4 | 5.4 y 8.5 (mayor tercero) | 18.31 | +1.95765×10−1 | 5:3 | 31 |
| 2.7 | 25.24 y 48.25 (semitona cromática) | 29.50 | +1.89653×10−1 | 8:5 | 50 |
| 1.3 | 5.3 y 6.5 (pequeño tercio) | 11.19 | -4.93956×10−2 | 3:2 | 19 |
| 1.2 | 9.5 y 10.9 (tono entero menor) | 15.26 | +1.10584×100 | 4:3 | 26 |
Temperamentos iguales
Ni la quinta justa ni el cuarto de coma significan una quinta es una fracción racional de la octava, pero existen varias afinaciones que se aproximan a la quinta por tal intervalo; estos son un subconjunto de los temperamentos iguales ("N-ET"), en los que la octava se divide en algún número (N) de igual amplitud intervalos
Los temperamentos iguales útiles como afinaciones de tono medio incluyen (en orden de aumento del ancho del generador) 19-ET (~1/3 de coma), 50-ET (~2/7 de coma), 31-ET (~1/4 de coma), 43-ET (~1/5 coma) y 55-ET (~1/6 coma). Sin embargo, cuanto más se aleja la afinación del significado de un cuarto de coma, menos relacionada está la afinación con los timbres armónicos, que se pueden superar templando los parciales para que coincidan con la afinación, lo que, sin embargo, solo es posible en sintetizadores electrónicos.
| C | C▪ | D. | D | D▪ | E. | E | E▪ | F | F▪ | G. | G | G▪ | A. | A | A▪ | B. | B | C. | C | |
| 1/4 coma: | 0.00 | 76.05 | 117.11 | 193.16 | 269.21 | 310.26 | 386.31 | 462.36 | 503.42 | 579.47 | 620.53 | 696.58 | 772.63 | 813.69 | 889.74 | 965.78 | 1006.84 | 1082.89 | 1123.95 | 1200,00 |
| 31-ET: | 0.00 | 77.42 | 116.13 | 193.55 | 270.97 | 309.68 | 387.10 | 464.52 | 503.23 | 580.65 | 619.35 | 696.77 | 774.19 | 812.90 | 890.32 | 967.74 | 1006.45 | 1083.87 | 1122.58 | 1200,00 |
Intervalos de lobo
Un número entero de quintas perfectas nunca sumará un número entero de octavas, porque son inconmensurables (ver Teorema fundamental de la aritmética). Si un número entero apilado de quintas perfectas está demasiado cerca de la octava, entonces uno de los intervalos que es enarmónicamente equivalente a una quinta debe tener un ancho diferente al de las otras quintas. Por ejemplo, para hacer que una escala cromática de 12 notas en afinación pitagórica cierre en la octava, uno de los intervalos de quinta debe estar rebajado ("desafinado") por la coma pitagórica; esta quinta alterada se llama quinta de lobo porque suena similar a una quinta en su tamaño de intervalo y parece una quinta desafinada. Sin embargo, en realidad es una sexta disminuida pitagórica (o una tercera aumentada en lugar de una cuarta), digamos el intervalo entre C y E♯.
Los intervalos de Wolf son un artefacto del diseño del teclado. Esto se puede mostrar más fácilmente usando un teclado isomorfo, como el que se muestra en la Figura 2.
En un teclado isomorfo, cualquier intervalo musical dado tiene la misma forma dondequiera que aparezca, excepto en los bordes. Aquí hay un ejemplo. En el teclado que se muestra en la Figura 2, desde cualquier nota dada, la nota que es una quinta perfecta más alta siempre está arriba y a la derecha adyacente a la nota dada. No hay intervalos de lobo dentro del lapso de notas de este teclado. El problema está en el borde, en la nota E♯. La nota que es una quinta perfecta más alta que E♯< /span> es B♯ , que no está incluido en el teclado que se muestra (aunque podría incluirse en un teclado más grande, ubicado justo a la derecha de A♯, manteniendo así el patrón de notas consistente del teclado). Porque no hay B♯ botón, al reproducir un E♯ acorde de potencia, uno debe elegir alguna otra nota, como C, para tocar en lugar de la B faltante♯.
Las condiciones de borde uniformes producen intervalos de lobo solo si el teclado isomórfico tiene menos botones por octava que la afinación tiene notas enarmónicamente distintas (Milne, 2007). Por ejemplo, el teclado isomorfo de la Figura 2 tiene 19 botones por octava, por lo que la condición de borde mencionada anteriormente, de E♯ a C, no es un intervalo de lobo en 12-ET, 17-ET o 19-ET; sin embargo, es un intervalo de lobo en 26-ET, 31-ET y 50-ET. En estas últimas afinaciones, el uso de la transposición electrónica podría mantener las notas de la tecla actual en los botones blancos del teclado isomórfico, de modo que estos intervalos de lobo rara vez se encontrarían en la música tonal, a pesar de la modulación a teclas exóticas.
Los teclados isomorfos exponen las propiedades invariables de las afinaciones de tono medio del temperamento sintónico de manera isomorfa (es decir, al exponer un intervalo dado con una sola forma consistente entre botones en cada octava, tecla y afinación) porque tanto el el teclado isomórfico y el temperamento son entidades bidimensionales (es decir, rango 2) (Milne, 2007). Los teclados de tecla N unidimensionales pueden exponer con precisión las propiedades invariantes de una única afinación N-ET unidimensional; por lo tanto, el teclado estilo piano unidimensional, con 12 teclas por octava, puede exponer las propiedades invariantes de una sola afinación: 12-ET.
Cuando la quinta perfecta tiene exactamente 700 centavos de ancho (es decir, templado por aproximadamente 1⁄11 de una coma sintónica, o exactamente 1⁄12 de una coma pitagórica), entonces la afinación es idéntica al familiar temperamento igual de 12 tonos. Esto aparece en la tabla anterior cuando R = 2:1.
Debido a los compromisos (y los intervalos de lobo) impuestos en las afinaciones de tono medio por el teclado unidimensional de estilo piano, los temperamentos buenos y, finalmente, el temperamento igual se hicieron más populares.
Usando nombres de intervalo estándar, doce quintos equivalen a seis octavas más una séptima aumentada; siete octavas son once quintos más un sexto disminuido. Dado esto, tres "tercios menores" en realidad son segundos aumentados (por ejemplo, B♭ a C♯), y cuatro "tercios principales" en realidad son cuartas disminuidas (por ejemplo, B a E♭). Varias tríadas (como B–E♭–F♯ y B♭–C♯–F) contienen estos dos intervalos y tienen quintas normales.
Meantones extendidos
Todas las afinaciones de tono medio entran en el rango de afinación válido del temperamento sintónico, por lo que todas las afinaciones de tono medio son afinaciones sintónicas. Todas las afinaciones sintónicas, incluidos los meantones, tienen un número conceptualmente infinito de notas en cada octava, es decir, siete notas naturales, siete notas agudas (F♯ to B♯), siete notas bemol (B♭ a F♭), notas dobles sostenidas, notas dobles bemoles, triples sostenidos y bemoles, etc. De hecho, los sostenidos y bemoles dobles son poco comunes, pero aún son necesarios; Los sostenidos y bemoles triples casi nunca se ven. En cualquier afinación sintónica que divida la octava en un pequeño número de intervalos más pequeños igualmente anchos (como 12, 19 o 31), esta infinidad de notas todavía existe, aunque algunas notas serán equivalentes. Por ejemplo, en 19-ET, E♯ y F♭ son del mismo tono.
Muchos instrumentos musicales son capaces de hacer distinciones de tono muy finas, como la voz humana, el trombón, cuerdas sin trastes como el violín y laúdes con trastes atados. Estos instrumentos se adaptan bien al uso de afinaciones de tono medio.
Por otro lado, el teclado del piano tiene solo doce dispositivos físicos de control de notas por octava, lo que lo hace poco adecuado para cualquier afinación que no sea 12-ET. Casi todos los problemas históricos con el temperamento del tono medio son causados por el intento de asignar el número infinito de notas por octava del tono medio a un número finito de teclas de piano. Esta es, por ejemplo, la fuente del "lobo quinto" discutido anteriormente. Al elegir qué notas asignar a las teclas negras del piano, es conveniente elegir aquellas notas que son comunes a un pequeño número de teclas estrechamente relacionadas, pero esto solo funcionará hasta el borde de la octava; al pasar a la siguiente octava, se debe usar un "quinto lobo" que no es tan ancho como los otros, como se discutió anteriormente.
La existencia del "quinto lobo" es una de las razones por las que, antes de la introducción del buen temperamento, la música instrumental generalmente permanecía en una serie de "seguros" tonalidades que no implican el "lobo quinto" (que generalmente se colocaba entre G♯ y E♭).
A lo largo del Renacimiento y la Ilustración, teóricos tan variados como Nicola Vicentino, Francisco de Salinas, Fabio Colonna, Marin Mersenne, Christiaan Huygens e Isaac Newton defendieron el uso de afinaciones de tono medio que se extendían más allá de las doce notas del teclado., y por lo tanto han llegado a ser llamados "extendidos" afinaciones de tono medio. Estos esfuerzos requirieron una extensión concomitante de los instrumentos de teclado para ofrecer medios para controlar más de 12 notas por octava, incluido el Archicembalo de Vincento, el clavicémbalo 19-ET de Mersenne, el sambuca 31-ET de Colonna y Clavicordio 31-ET de Huygens. Otros instrumentos extendieron el teclado en solo unas pocas notas. Algunos clavicémbalos y órganos de época se han dividido D♯< /span>/E♭ claves, de modo que tanto E mayor/C♯ menor (4 sostenidos) como E♭ mayor/C menor (3 bemoles) se pueden tocar sin quintas de lobo. Muchos de esos instrumentos también tienen G♯< /span>/A♭ llaves, y algunos tienen las cinco llaves accidentales divididas.
Todos estos instrumentos alternativos eran "complicados" y "engorroso" (Isacoff, 2003), debido a que (a) no es isomorfo y (b) no tiene la capacidad de transponer electrónicamente, lo que puede reducir significativamente la cantidad de botones de control de notas necesarios en un teclado isomorfo (Plamondon, 2009). Ambas críticas podrían abordarse con instrumentos de teclado isomórficos electrónicos (como el teclado bloqueador de hardware de código abierto), que podrían ser más simples, menos engorrosos y más expresivos que los instrumentos de teclado existentes.
Uso del temperamento de tono medio
Las referencias a sistemas de afinación que posiblemente podrían referirse al significado se publicaron ya en 1496 (Gafori), y Aron (1523) se refiere inequívocamente al significado. Sin embargo, las primeras descripciones de afinación de Meantone matemáticamente precisas se encuentran en tratados de finales del siglo XVI de Francisco de Salinas y Gioseffo Zarlino. Salinas (en De musica libri septem, 1577) describe tres temperamentos de tono medio diferentes: el sistema de tercera coma, el sistema de dos séptimas comas y el sistema de cuartos de coma. Él es el probable inventor del sistema de la tercera coma, mientras que él y Zarlino escribieron sobre el sistema de dos séptimas comas, aparentemente de forma independiente. Lodovico Fogliano menciona el sistema de cuarto de coma, pero no ofrece una discusión al respecto.
En el pasado, los temperamentos de tono medio a veces se usaban o se los denominaba con otros nombres o descripciones. Por ejemplo, en 1691 Christiaan Huygens escribió su "Lettre touchant le cycle harmonique" ("Carta sobre el ciclo armónico") con el propósito de introducir lo que él creía ser una nueva división de la octava. En esta carta, Huygens se refirió varias veces, de manera comparativa, a un arreglo de afinación convencional, que denominó diversamente como "temperament ordinaire", o "el que todos usan". Pero Huygens' La descripción de este arreglo convencional fue bastante precisa y es claramente identificable con lo que ahora se clasifica como (cuarto de coma) significa temperamento de tono.
Aunque el meantone es más conocido como un entorno de afinación asociado con la música anterior del Renacimiento y el Barroco, existe evidencia del uso continuo del meantone como temperamento de teclado hasta mediados del siglo XIX. El temperamento de tono medio ha tenido un renacimiento considerable para la interpretación de música antigua a fines del siglo XX y en obras recién compuestas que exigen específicamente tono medio de compositores como John Adams, György Ligeti y Douglas Leedy.
Contenido relacionado
Fuerza de Van der Waals
Varianza de Allan
Ani DiFranco
