Teletransportación cuántica

ImprimirCitar

Fenómeno físico

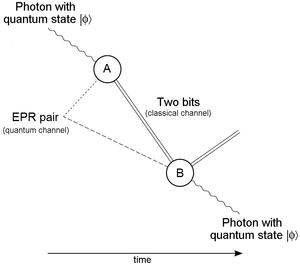
La teletransportación cuántica es una técnica para transferir información cuántica de un emisor en un lugar a un receptor a cierta distancia. Si bien la teletransportación se presenta comúnmente en la ciencia ficción como un medio para transferir objetos físicos de un lugar a otro, la teletransportación cuántica solo transfiere información cuántica. El remitente no tiene que conocer el estado cuántico particular que se transfiere. Además, la ubicación del destinatario puede ser desconocida, pero para completar la teletransportación cuántica, se debe enviar información clásica del remitente al receptor. Debido a que es necesario enviar información clásica, la teletransportación cuántica no puede ocurrir más rápido que la velocidad de la luz.

Uno de los primeros artículos científicos que investiga la teletransportación cuántica es "Teletransportación de un estado cuántico desconocido a través de canales duales clásicos y de Einstein-Podolsky-Rosen" publicado por C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres y W. K. Wootters en 1993, en el que utilizaron métodos de comunicación dual para enviar/recibir información cuántica. Fue realizado experimentalmente en 1997 por dos grupos de investigación, dirigidos por Sandu Popescu y Anton Zeilinger, respectivamente.

Se han realizado determinaciones experimentales de la teletransportación cuántica en el contenido de la información, incluidos fotones, átomos, electrones y circuitos superconductores, así como en la distancia, siendo 1400 km (870 mi) la distancia más larga de teletransportación exitosa realizada por el grupo de Jian- Wei Pan usando el satélite Micius para la teletransportación cuántica basada en el espacio.

Resumen no técnico

Diagrama de los componentes básicos utilizados para la teleportación cuántica

En cuestiones relacionadas con la teoría de la información cuántica, es conveniente trabajar con la unidad de información más simple posible: el sistema de dos estados del qubit. El qubit funciona como el análogo cuántico de la parte computacional clásica, el bit, ya que puede tener un valor de medición de tanto un 0 como un 1, mientras que el bit clásico puede solo puede medirse como un 0 o un 1. El sistema cuántico de dos estados busca transferir información cuántica de un lugar a otro sin perder la información y preservando la calidad de esta información. Este proceso implica el movimiento de la información entre portadores y no el movimiento de los portadores reales, similar al proceso tradicional de comunicaciones, ya que dos partes permanecen estacionarias mientras la información (medios digitales, voz, texto, etc.) se está transfiriendo, contrariamente a las implicaciones de la palabra "teletransporte". Los principales componentes necesarios para la teletransportación incluyen un remitente, la información (un qubit), un canal tradicional, un canal cuántico y un receptor. Un dato interesante es que el remitente no necesita conocer el contenido exacto de la información que se le envía. El postulado de medición de la mecánica cuántica: cuando se realiza una medición sobre un estado cuántico, cualquier medición posterior 'colapsará'. o que el estado observado se perderá—crea una imposición dentro de la teletransportación: si un remitente realiza una medición de su información, el estado podría colapsar cuando el receptor obtiene la información ya que el estado ha cambiado desde que el remitente realizó la medición inicial.

Para la teletransportación real, se requiere que se cree un estado cuántico entrelazado o estado Bell para que se transfiera el qubit. El entrelazamiento impone correlaciones estadísticas entre sistemas físicos distintos al crear o colocar dos o más partículas separadas en un solo estado cuántico compartido. Este estado intermedio contiene dos partículas cuyos estados cuánticos son dependientes entre sí ya que forman una conexión: si una partícula se mueve, la otra partícula se moverá con ella. Cualquier cambio que sufra una partícula del entrelazamiento, la otra partícula también sufrirá ese cambio, haciendo que las partículas entrelazadas actúen como un estado cuántico. Estas correlaciones se mantienen incluso cuando las mediciones se eligen y realizan de forma independiente, fuera del contacto causal entre sí, como se verificó en los experimentos de prueba de Bell. Por lo tanto, una observación resultante de una elección de medición realizada en un punto del espacio-tiempo parece afectar instantáneamente los resultados en otra región, aunque la luz aún no haya tenido tiempo de recorrer la distancia; una conclusión aparentemente en desacuerdo con la relatividad especial. Esto se conoce como la paradoja EPR. Sin embargo, tales correlaciones nunca pueden usarse para transmitir información más rápido que la velocidad de la luz, una declaración encapsulada en el teorema de no comunicación. Por lo tanto, la teletransportación en su conjunto nunca puede ser superlumínica, ya que un qubit no puede reconstruirse hasta que llegue la información clásica que lo acompaña.

El emisor luego preparará la partícula (o información) en el qubit y la combinará con una de las partículas entrelazadas del estado intermedio, provocando un cambio del estado cuántico entrelazado. El estado cambiado de la partícula entrelazada se envía luego a un analizador que medirá este cambio del estado entrelazado. El "cambio" la medición permitirá al receptor recrear la información original que tenía el remitente, lo que dará como resultado que la información sea teletransportada o transportada entre dos personas que tienen ubicaciones diferentes. Dado que la información cuántica inicial se "destruye" a medida que se convierte en parte del estado entrelazado, el teorema de no clonación se mantiene ya que la información se recrea desde el estado entrelazado y no se copia durante la teletransportación.

El canal cuántico es el mecanismo de comunicación que se usa para toda la transmisión de información cuántica y es el canal que se usa para la teletransportación (la relación del canal cuántico con el canal de comunicación tradicional es similar a que el qubit es el análogo cuántico del bit clásico). Sin embargo, además del canal cuántico, también se debe usar un canal tradicional para acompañar un qubit para "preservar" la información cuántica. Cuando se realiza la medición del cambio entre el qubit original y la partícula entrelazada, el resultado de la medición debe ser transportado por un canal tradicional para que la información cuántica pueda reconstruirse y el receptor pueda obtener la información original. Debido a esta necesidad del canal tradicional, la velocidad de teletransportación no puede ser más rápida que la velocidad de la luz (por lo tanto, no se viola el teorema de no comunicación). La principal ventaja de esto es que los estados de Bell se pueden compartir usando fotones de láseres, lo que hace posible la teletransportación a través del espacio abierto sin necesidad de enviar información a través de cables físicos o fibras ópticas.

Los estados cuánticos se pueden codificar en varios grados de libertad de los átomos. Por ejemplo, los qubits se pueden codificar en los grados de libertad de los electrones que rodean el núcleo atómico o en los grados de libertad del propio núcleo. Por lo tanto, realizar este tipo de teletransportación requiere un stock de átomos en el sitio de recepción, disponible para tener qubits impresos en ellos.

A partir de 2015, los estados cuánticos de fotones individuales, modos de fotones, átomos individuales, conjuntos atómicos, centros de defectos en sólidos, electrones individuales y circuitos superconductores se han empleado como portadores de información.

Comprender la teletransportación cuántica requiere una buena base en álgebra lineal de dimensión finita, espacios de Hilbert y matrices de proyección. Un qubit se describe utilizando un espacio vectorial de valor numérico complejo bidimensional (un espacio de Hilbert), que es la base principal para las manipulaciones formales que se indican a continuación. No se requiere absolutamente un conocimiento práctico de la mecánica cuántica para comprender las matemáticas de la teletransportación cuántica, aunque sin tal conocimiento, el significado más profundo de las ecuaciones puede seguir siendo bastante misterioso.

Protocolo

Diagrama para teletransportación cuántica de un fotón

Los recursos necesarios para la teletransportación cuántica son un canal de comunicación capaz de transmitir dos bits clásicos, un medio de generar un estado enredado de Bell de qubits y distribuir a dos lugares diferentes, realizando una medición de Bell en uno de los qubits estatales de Bell, y manipulando el estado cuántico del otro cuarto del par. Por supuesto, también debe haber algún qubit de entrada (en el estado cuántico $|phi rangle$ Para ser teletransportado. El protocolo es el siguiente:

A El estado de Bell se genera con un cuarto enviado a la ubicación A y el otro enviado a la ubicación B.
A Medición de Bell del qubit estatal Bell y el qubit a ser teletransportado ( $|phi rangle$ ) se realiza en la ubicación A. Esto produce uno de los cuatro resultados de medición que se pueden codificar en dos bits clásicos de información. Ambos codos en la ubicación A son descartados.
Usando el canal clásico, los dos bits se envían de A a B. (Este es el único paso potencialmente largo después del paso 1 ya que la transferencia de información está limitada por la velocidad de la luz.)
Como resultado de la medición realizada en la ubicación A, el qubit de estado de Bell en la ubicación B está en uno de los cuatro estados posibles. De estos cuatro estados posibles, uno es idéntico al estado cuántico original $|phi rangle$ y los otros tres están estrechamente relacionados. La identidad del estado realmente obtenido se codifica en dos partes clásicas y se envía a la ubicación B. El qubit de estado de Bell en la ubicación B se modifica en una de tres maneras, o no, que resulta en un qubit idéntico a $|phi rangle$ , el estado del qubit que fue elegido para la teletransportación.

Vale la pena notar que el protocolo anterior asume que los qubits son direccionables individualmente, lo que significa que los qubits son distinguibles y etiquetados físicamente. Sin embargo, puede haber situaciones en las que dos qubits idénticos no se puedan distinguir debido a la superposición espacial de sus funciones de onda. Bajo esta condición, los qubits no pueden controlarse ni medirse individualmente. Sin embargo, un protocolo de teletransportación análogo al descrito anteriormente aún puede implementarse (condicionalmente) mediante la explotación de dos qubits preparados de forma independiente, sin necesidad de un estado Bell inicial. Esto se puede hacer abordando los grados de libertad internos de los qubits (p. ej., espines o polarizaciones) mediante mediciones espacialmente localizadas realizadas en regiones separadas A y B compartidas por las funciones de onda de los dos qubits indistinguibles.

Resultados y registros experimentales

El trabajo realizado en 1998 verificó las predicciones iniciales y la distancia de teletransportación se incrementó en agosto de 2004 a 600 metros, utilizando fibra óptica. Posteriormente, la distancia récord para la teletransportación cuántica se ha incrementado gradualmente a 16 kilómetros (9,9 mi), luego a 97 km (60 mi) y ahora es de 143 km (89 mi), establecida en experimentos al aire libre en las Islas Canarias, realizada entre los dos observatorios astronómicos del Instituto de Astrofísica de Canarias. Ha habido un récord reciente (a partir de septiembre de 2015) utilizando detectores de nanocables superconductores que alcanzaron una distancia de 102 km (63 mi) sobre fibra óptica. Para los sistemas de materiales, la distancia récord es de 21 metros (69 pies).

Una variante de teletransportación llamada "destino abierto" la teletransportación, con receptores ubicados en múltiples ubicaciones, se demostró en 2004 utilizando el entrelazamiento de cinco fotones. También se ha realizado la teletransportación de un estado compuesto de dos qubits individuales. En abril de 2011, los experimentadores informaron que habían demostrado la teletransportación de paquetes de ondas de luz hasta un ancho de banda de 10 MHz mientras conservaban estados de superposición fuertemente no clásicos. En agosto de 2013, el logro de "totalmente determinista" Se informó de la teletransportación cuántica, utilizando una técnica híbrida. El 29 de mayo de 2014, los científicos anunciaron una forma fiable de transferir datos mediante teletransportación cuántica. La teletransportación cuántica de datos se había realizado antes, pero con métodos muy poco fiables. El 26 de febrero de 2015, científicos de la Universidad de Ciencia y Tecnología de China en Hefei, dirigidos por Chao-yang Lu y Jian-Wei Pan, llevaron a cabo el primer experimento de teletransportación de múltiples grados de libertad de una partícula cuántica. Consiguieron teletransportar la información cuántica de un conjunto de átomos de rubidio a otro conjunto de átomos de rubidio a una distancia de 150 metros (490 pies) utilizando fotones entrelazados. En 2016, los investigadores demostraron la teletransportación cuántica con dos fuentes independientes que están separadas por 6,5 km (4,0 mi) en la red de fibra óptica de Hefei. En septiembre de 2016, investigadores de la Universidad de Calgary demostraron la teletransportación cuántica a través de la red de fibra metropolitana de Calgary a una distancia de 6,2 km (3,9 mi). En diciembre de 2020, como parte de la colaboración INQNET, los investigadores lograron la teletransportación cuántica en una distancia total de 44 km (27,3 mi) con fidelidades superiores al 90 %.

Los investigadores también han utilizado con éxito la teletransportación cuántica para transmitir información entre nubes de átomos de gas, algo notable porque las nubes de gas son conjuntos atómicos macroscópicos.

También es posible teletransportarse a operaciones lógicas, ver teletransportación de puerta cuántica. En 2018, los físicos de Yale demostraron una operación CNOT teletransportada determinista entre qubits codificados lógicamente.

Propuesta teóricamente por primera vez en 1993, la teletransportación cuántica se ha demostrado desde entonces en muchas formas diferentes. Se ha llevado a cabo utilizando estados de dos niveles de un solo fotón, un solo átomo y un ion atrapado -entre otros objetos cuánticos- y también utilizando dos fotones. En 1997, dos grupos lograron experimentalmente la teletransportación cuántica. El primer grupo, dirigido por Sandu Popescu, se basó en Italia. Un grupo experimental dirigido por Anton Zeilinger lo siguió unos meses después.

Los resultados obtenidos de los experimentos realizados por el grupo de Popescu concluyeron que los canales clásicos por sí solos no podían replicar la teletransportación de un estado de polarización lineal y un estado de polarización elíptica. La medición del estado de Bell distinguió entre los cuatro estados de Bell, lo que puede permitir una tasa de éxito de teletransportación del 100%, en una representación ideal.

El grupo de Zeilinger produjo un par de fotones entrelazados mediante la implementación del proceso de conversión descendente paramétrica. Para garantizar que los dos fotones no se puedan distinguir por sus tiempos de llegada, los fotones se generaron utilizando un haz de bombeo pulsado. Luego, los fotones se enviaron a través de filtros de ancho de banda estrecho para producir un tiempo de coherencia que es mucho más largo que la duración del pulso de bombeo. Luego utilizaron una interferometría de dos fotones para analizar el entrelazamiento de modo que la propiedad cuántica pudiera reconocerse cuando se transfiere de un fotón a otro.

El foton 1 fue polarizado a 45° en el primer experimento realizado por el grupo de Zeilinger. La teletransportación cuántica se verifica cuando ambos fotones se detectan en el ${displaystyle |Psi ^{-}rangle _{12}}$ estado, que tiene una probabilidad de 25%. Dos detectores, f1 y f2, se colocan detrás del separador de vigas, y la grabación de la coincidencia identificará el ${displaystyle |Psi ^{-}rangle _{12}}$ estado. Si hay una coincidencia entre los detectores f1 y f2, se prevé que el foton 3 se polarizará a un ángulo de 45°. Photon 3 se pasa a través de un separador de haz polarizante que selecciona +45° y -45° polarización. Si la teletransportación cuántica ha ocurrido, sólo el detector d2, que está a la salida +45°, registrará una detección. Detector d1, ubicado en la salida -45°, no detectará un foton. Si hay una coincidencia entre d2f1f2, con el análisis de 45°, y una falta de una coincidencia d1f2, con un análisis de -45°, es prueba de que la información del fotón polarizado 1 ha sido teletransportada al fotón 3 usando teletransportación cuántica.

Teletransportación cuántica de más de 143 km

El grupo de Zeilinger desarrolló un experimento utilizando feed-forward activo en tiempo real y dos enlaces ópticos de espacio libre, cuántico y clásico, entre las islas canarias de La Palma y Tenerife, a una distancia de más de 143 kilómetros. Para lograr la teletransportación, se implementaron una fuente de par de fotones entrelazados con polarización no correlacionada en frecuencia, detectores de fotones individuales de ruido ultra bajo y sincronización de reloj asistida por entrelazamiento. Las dos ubicaciones se entrelazaron para compartir el estado auxiliar:

{displaystyle |Psi ^{-}rangle _{23}={frac {1}{surd 2}}((|Hrangle _{2}|Vrangle _{3})-(|Vrangle _{2}|Hrangle _{3}))}

La Palma y Tenerife se pueden comparar con los personajes cuánticos Alice y Bob. Alice y Bob comparten el estado entrelazado anterior, con el fotón 2 con Alice y el fotón 3 con Bob. Un tercero, Charlie, proporciona el fotón 1 (el fotón de entrada) que será teletransportado a Alice en el estado de polarización generalizada:

{displaystyle |phi rangle _{1}=alpha |Hrangle _{1}+beta |Vrangle _{1}}

donde los números complejos $alpha$ y $beta$ son desconocidos para Alice o Bob.

Alice realizará una medición de Bell-state (BSM) que proyecta aleatoriamente los dos fotones en uno de los cuatro estados de Bell con cada uno con una probabilidad de 25%. Photon 3 será proyectado sobre $|phirangle$ , el estado de entrada. Alice transmite el resultado de la BSM a Bob, a través del canal clásico, donde Bob es capaz de aplicar la operación unitaria correspondiente para obtener foton 3 en el estado inicial de foton 1. Bob no tendrá que hacer nada si detecta el ${displaystyle |psi ^{-}rangle _{12}}$ estado. Bob tendrá que aplicar un $pi$ cambio de fase al fotón 3 entre el componente horizontal y vertical si ${displaystyle |psi ^{+}rangle _{12}}$ el estado es detectado.

Los resultados del grupo de Zeilinger concluyeron que la fidelidad promedio (superposición del estado teletransportado ideal con la matriz de densidad medida) fue de 0,863 con una desviación estándar de 0,038. La atenuación del enlace durante sus experimentos varió entre 28,1 dB y 39,0 dB, como resultado de los fuertes vientos y los rápidos cambios de temperatura. A pesar de la alta pérdida en el canal de espacio libre cuántico, la fidelidad promedio superó el límite clásico de 2/3. Por lo tanto, el grupo de Zeilinger demostró con éxito la teletransportación cuántica en una distancia de 143 km.

Teletransportación cuántica a través del río Danubio

En 2004, se llevó a cabo un experimento de teletransportación cuántica a través del río Danubio en Viena, un total de 600 metros. Se instaló un cable de fibra óptica de 800 metros de largo en un sistema de alcantarillado público debajo del río Danubio, y estuvo expuesto a cambios de temperatura y otras influencias ambientales. Alice debe realizar una medición conjunta del estado de Bell (BSM) en el fotón b, el fotón de entrada, y el fotón c, su parte del par de fotones entrelazados (fotones c y d). El fotón d, el fotón receptor de Bob, contendrá toda la información sobre el fotón b de entrada, excepto una rotación de fase que depende del estado que observó Alice. Este experimento implementó un sistema de avance activo que envía los resultados de las mediciones de Alice a través de un canal de microondas clásico con un modulador electroóptico rápido para replicar exactamente el fotón de entrada de Alice. La fidelidad de teletransportación obtenida del estado de polarización lineal a 45° varió entre 0,84 y 0,90, muy por encima del límite de fidelidad clásico de 0,66.

Teletransportación cuántica determinista con átomos

Para este proceso se requieren tres codos: el codo fuente del remitente, el codo auxiliar y el codo blanco del receptor, que se enreda máximamente con el codo auxiliar. Para este experimento, ${displaystyle {ce {^{40}Ca+}}}$ Se utilizaron iones como codos. Iones 2 y 3 están preparados en el estado de Bell ${displaystyle |psi ^{+}rangle _{23}={frac {1}{sqrt {2}}}(|0rangle _{2}|1rangle _{3}+|1rangle _{2}|0rangle _{3})}$ . El estado del ión 1 se prepara arbitrariamente. Los estados cuánticos de los iones 1 y 2 se miden iluminando con luz en una longitud de onda específica. Las fidelidades obtenidas para este experimento oscilaron entre el 73% y el 76%. Esto es mayor que la máxima fidelidad media posible del 66,7% que se puede obtener utilizando recursos completamente clásicos.

Teletransportación cuántica de tierra a satélite

El estado cuántico siendo teletransportado en este experimento es ${displaystyle |chi rangle _{1}=alpha |Hrangle _{1}+beta |Vrangle _{1}}$ , donde $alpha$ y $beta$ son números complejos desconocidos, $|Hrangle$ representa el estado de polarización horizontal, y $|Vrangle$ representa el estado de polarización vertical. El qubit preparado en este estado se genera en un laboratorio en Ngari, Tibet. El objetivo era teletransportar la información cuántica del qubit al satélite Micius que fue lanzado el 16 de agosto de 2016, a una altitud de unos 500 km. Cuando se realiza una medición del estado de Bell en fotones 1 y 2 y el estado resultante es ${displaystyle |phi ^{+}rangle _{12}={frac {1}{sqrt {2}}}(|Hrangle _{1}|Hrangle _{2}+|Vrangle _{1}|Vrangle _{2}))}$ , foton 3 lleva este estado deseado. Si el estado de Bell detecta ${displaystyle |phi ^{-}rangle _{12}={frac {1}{sqrt {2}}}(|Hrangle _{1}|Hrangle _{2}-|Vrangle _{1}|Vrangle _{2})}$ , luego un cambio de fase $pi$ se aplica al estado para obtener el estado cuántico deseado. La distancia entre la estación de tierra y el satélite cambia de tan solo 500 km a tan grande como 1.400 km. Debido a la distancia cambiante, la pérdida del canal del enlace varía entre 41 dB y 52 dB. La fidelidad promedio obtenida de este experimento fue de 0,80 con una desviación estándar de 0.01. Por lo tanto, este experimento estableció con éxito un enlace de tierra a satélite a lo largo de una distancia de 500 a 1.400 km utilizando teletransportación cuántica. Este es un paso esencial para crear un Internet cuántico a escala mundial.

Presentación formal

Hay una variedad de formas en las que el protocolo de teletransportación se puede escribir matemáticamente. Algunos son muy compactos pero abstractos, y otros son detallados pero directos y concretos. La presentación a continuación es de la última forma: detallada, pero tiene la ventaja de mostrar cada estado cuántico de manera simple y directa. Las secciones posteriores revisan notaciones más compactas.

El protocolo de teletransportación comienza con un estado cuántico o qubit $|psi rangle$ En posesión de Alice, quiere transmitirle a Bob. Este qubit se puede escribir generalmente, en la notación del sujetador, como:

|psirangle_C = alpha |0rangle_C + beta|1rangle_C.

El subíndice C anterior se usa solo para distinguir este estado de A y B, a continuación.

A continuación, el protocolo requiere que Alice y Bob compartan un estado de enredo máximo. Este estado se fija de antemano, de mutuo acuerdo entre Alice y Bob, y puede ser cualquiera de los cuatro estados de Bell que se muestran. No importa cuál.

|Phi^+rangle_{AB} = frac{1}{sqrt{2}} (|0rangle_A otimes |0rangle_{B} + |1rangle_A otimes |1rangle_{B})

|Psi^+rangle_{AB} = frac{1}{sqrt{2}} (|0rangle_A otimes |1rangle_{B} + |1rangle_A otimes |0rangle_{B})

|Psi^-rangle_{AB} = frac{1}{sqrt{2}} (|0rangle_A otimes |1rangle_{B} - |1rangle_A otimes |0rangle_{B})

|Phi^-rangle_{AB} = frac{1}{sqrt{2}} (|0rangle_A otimes |0rangle_{B} - |1rangle_A otimes |1rangle_{B})

En lo siguiente, asuma que Alice y Bob comparten el estado $|Phi^+rangle_{AB}.$ Alice obtiene una de las partículas en el par, con la otra yendo a Bob. (Esto se implementa preparando las partículas juntas y disparando a Alice y Bob de una fuente común.) Los subscriptos A y B en el estado enredado se refieren a la partícula de Alice o Bob.

En este punto, Alice tiene dos partículas (C, la que quiere teletransportar, y A, una del par entrelazado), y Bob tiene una partícula, B. En el sistema total, el estado de estas tres partículas viene dado por

{displaystyle |psi rangle _{C}otimes |Phi ^{+}rangle _{AB}=(alpha |0rangle _{C}+beta |1rangle _{C})otimes {frac {1}{sqrt {2}}}(|0rangle _{A}otimes |0rangle _{B}+|1rangle _{A}otimes |1rangle _{B}).}

Alice luego hará una medición local en la base de Bell (es decir, los cuatro estados de Bell) en las dos partículas que posee. Para aclarar el resultado de su medición, es mejor escribir el estado de los dos qubits de Alice como superposiciones de la base de Bell. Esto se hace utilizando las siguientes identidades generales, que se verifican fácilmente:

|0rangle otimes |0rangle = frac{1}{sqrt{2}} (|Phi^+rangle + |Phi^-rangle),

|0rangle otimes |1rangle = frac{1}{sqrt{2}} (|Psi^+rangle + |Psi^-rangle),

|1rangle otimes |0rangle = frac{1}{sqrt{2}} (|Psi^+rangle - |Psi^-rangle),

|1rangle otimes |1rangle = frac{1}{sqrt{2}} (|Phi^+rangle - |Phi^-rangle).

Después de ampliar la expresión ${textstyle {begin{aligned}|&psi rangle _{C}otimes |Phi ^{+}rangle _{AB}end{aligned}}}$ , uno aplica estas identidades a los codos con A y C subscriptos. En particular,

{displaystyle alpha {frac {1}{sqrt {2}}}|0rangle _{C}otimes |0rangle _{A}otimes |0rangle _{B}=alpha {frac {1}{2}}(|Phi ^{+}rangle _{CA}+|Phi ^{-}rangle _{CA})otimes |0rangle _{B},}

ABC

{displaystyle {begin{aligned}|&psi rangle _{C}otimes |Phi ^{+}rangle _{AB} =\{frac {1}{2}}{Big lbrack } &|Phi ^{+}rangle _{CA}otimes (alpha |0rangle _{B}+beta |1rangle _{B}) + |Phi ^{-}rangle _{CA}otimes (alpha |0rangle _{B}-beta |1rangle _{B})\ + &|Psi ^{+}rangle _{CA}otimes (alpha |1rangle _{B}+beta |0rangle _{B}) + |Psi ^{-}rangle _{CA}otimes (alpha |1rangle _{B}-beta |0rangle _{B}){Big rbrack }.\end{aligned}}}

Tenga en cuenta que las tres partículas todavía están en el mismo estado total ya que no se han realizado operaciones. Más bien, lo anterior es solo un cambio de base en la parte del sistema de Alice. La teletransportación real ocurre cuando Alice mide sus dos qubits A,C, en la base de Bell

Un simple circuito cuántico que mapea uno de los cuatro estados de Bell (el par EPR en la imagen) en uno de los cuatro estados de base computacional de dos codos. El circuito consta de una puerta CNOT seguida de una operación Hadamard. En las salidas, a y b tomar valores de 0 o 1.

{displaystyle |Phi ^{+}rangle _{CA},|Phi ^{-}rangle _{CA},|Psi ^{+}rangle _{CA},|Psi ^{-}rangle _{CA}.}

Equivalentemente, la medición puede hacerse en la base computacional, ${displaystyle {|0rangle|1rangle }}$ , mediante la asignación de cada Estado de Bell único a uno de ${displaystyle {|0rangle otimes |0rangle|0rangle otimes |1rangle|1rangle otimes |0rangle|1rangle otimes |1rangle }}$ con el circuito cuántico de la figura a la derecha.

Dada la expresión anterior, evidentemente el resultado de la medición (local) de Alice es que el estado de tres partículas colapsaría a uno de los siguientes cuatro estados (con la misma probabilidad de obtener cada uno):

${displaystyle |Phi ^{+}rangle _{CA}otimes (alpha |0rangle _{B}+beta |1rangle _{B})}$
${displaystyle |Phi ^{-}rangle _{CA}otimes (alpha |0rangle _{B}-beta |1rangle _{B})}$
${displaystyle |Psi ^{+}rangle _{CA}otimes (alpha |1rangle _{B}+beta |0rangle _{B})}$
${displaystyle |Psi ^{-}rangle _{CA}otimes (alpha |1rangle _{B}-beta |0rangle _{B})}$

Las dos partículas de Alice ahora están entrelazadas entre sí, en uno de los cuatro estados de Bell, y el entrelazamiento que originalmente compartían las partículas de Alice y Bob ahora está roto. La partícula de Bob adopta uno de los cuatro estados de superposición que se muestran arriba. Observe cómo el qubit de Bob se encuentra ahora en un estado que se asemeja al estado para ser teletransportado. Los cuatro estados posibles para el qubit de Bob son imágenes unitarias del estado a teletransportar.

El resultado de la medición de Bell de Alice le dice en cuál de los cuatro estados anteriores se encuentra el sistema. Ahora puede enviar su resultado a Bob a través de un canal clásico. Dos bits clásicos pueden comunicar cuál de los cuatro resultados obtuvo.

Después de que Bob reciba el mensaje de Alice, él sabrá cuál de los cuatro estados está en su partícula. Usando esta información, realiza una operación unitaria en su partícula para transformarla en el estado deseado $alpha |0rangle_B + beta|1rangle_B$ :

Si Alice indica que su resultado es ${displaystyle |Phi ^{+}rangle _{CA}}$ , Bob sabe que su codo ya está en el estado deseado y no hace nada. Esto equivale a la operación trivial unitaria, el operador de identidad.
Si el mensaje indica ${displaystyle |Phi ^{-}rangle _{CA}}$ , Bob enviaría su codo a través de la puerta cuántica unitaria dada por la matriz Pauli

sigma_3 = begin{bmatrix} 1 & 0 \ 0 & -1end{bmatrix}

para recuperar el estado.

Si el mensaje de Alice corresponde a ${displaystyle |Psi ^{+}rangle _{CA}}$ , Bob aplica la puerta

sigma_1 = begin{bmatrix} 0 & 1 \ 1 & 0end{bmatrix}

a su qubit.

Por último, para el caso restante, la puerta correspondiente es dada por

{displaystyle sigma _{3}sigma _{1}=-sigma _{1}sigma _{3}=isigma _{2}={begin{bmatrix}0&1\-1&0end{bmatrix}}.}

Así se logra la teletransportación. Las tres puertas mencionadas anteriormente corresponden a rotaciones de π radianes (180°) sobre los ejes apropiados (X, Y y Z) en la imagen de esfera de Bloch de un qubit.

Algunos comentarios:

Después de esta operación, el qubit de Bob asumirá el estado $|psirangle_B= alpha |0rangle_B + beta|1rangle_B$ , y el qubit de Alice se convierte en una parte (sin definir) de un estado enredado. La teletransportación no resulta en la copia de qubits, y por lo tanto es consistente con el teorema sin cierre.
No hay transferencia de materia o energía involucrada. La partícula de Alice no ha sido trasladada físicamente a Bob; sólo su estado ha sido transferido. El término "teleportación", acuñado por Bennett, Brassard, Crépeau, Jozsa, Peres y Wootters, refleja la indistinguibilidad de partículas mecánicas cuánticas.
Por cada cuarto teletransportado, Alice necesita enviar a Bob dos partes clásicas de información. Estos dos bits clásicos no llevan información completa sobre el qubit siendo teletransportado. Si un eavesdropper intercepta los dos bits, puede saber exactamente lo que Bob necesita hacer para recuperar el estado deseado. Sin embargo, esta información es inútil si no puede interactuar con la partícula enredada en posesión de Bob.

Notaciones alternativas

Teleportación cuántica en su forma diagramática. empleando la notación gráfica Penrose. Formalmente, tal computación tiene lugar en una categoría compacta de daga. Esto resulta en la descripción abstracta de la teleportación cuántica empleada en la mecánica cuántica categórica.

Representación del circuito cuántico para la teletransportación de un estado cuántico, como se describe anteriormente. El circuito consume el

{displaystyle |Phi ^{+}rangle }

Bell state y el qubit a teleport como entrada, y consta de CNOT, Hadamard, dos medidas de dos cuartos, y finalmente, dos puertas con control clásico: a Pauli X, y a Pauli Z, lo que significa que si el resultado de la medición fue

|1rangle

, entonces la puerta de control clásico Pauli es ejecutada. Después de que el circuito haya terminado, el valor

{displaystyle |psi rangle _{C}}

se habrá mudado a, o teletransportado a

{displaystyle |psi rangle _{B}}

, y

{displaystyle |psi rangle _{C}}

tendrá su valor fijado a

|0rangle

|1rangle

, dependiendo del resultado de la medición en ese qubit.
Este circuito también se puede utilizar para intercambio de enredamiento, si

{displaystyle |psi rangle _{C}}

es uno de los codos que componen un estado enredado, como se describe en el texto.

Hay una variedad de notaciones diferentes en uso que describen el protocolo de teletransportación. Uno común es mediante el uso de la notación de puertas cuánticas.

En la derivación anterior, la transformación unitaria que es el cambio de base (de la base del producto estándar a la base de Bell) se puede escribir utilizando puertas cuánticas. El cálculo directo muestra que esta puerta está dada por

{displaystyle G=(Hotimes I)operatorname {CNOT} }

Donde H es la puerta de un cuarto de Walsh-Hadamard y ${displaystyle operatorname {CNOT} }$ es la puerta NO Controlada.

Intercambio de enredos

La teletransportación se puede aplicar no solo a los estados puros, sino también a los estados mixtos, que se pueden considerar como el estado de un único subsistema de un par entrelazado. El llamado intercambio de entrelazamiento es un ejemplo simple e ilustrativo.

Si Alice y Bob comparten un par entrelazado, y Bob teletransporta su partícula a Carol, entonces la partícula de Alice ahora está entrelazada con la partícula de Carol. Esta situación también se puede ver simétricamente de la siguiente manera:

Alice y Bob comparten un par entrelazado, y Bob y Carol comparten un par entrelazado diferente. Ahora permita que Bob realice una medición proyectiva en sus dos partículas en la base de Bell y comunique el resultado a Carol. Estas acciones son precisamente el protocolo de teletransportación descrito anteriormente con la primera partícula de Bob, la que se enredó con la partícula de Alice, como el estado a teletransportar. Cuando Carol termina el protocolo, ahora tiene una partícula con el estado teletransportado, es decir, un estado enredado con la partícula de Alice. Por lo tanto, aunque Alice y Carol nunca interactuaron entre sí, sus partículas ahora están entrelazadas.

Bob Coecke ha proporcionado una derivación esquemática detallada del intercambio de entrelazamiento, presentada en términos de mecánica cuántica categórica.

Algoritmo para intercambiar pares de campanas

Una aplicación importante del intercambio de entrelazamiento es la distribución de estados de Bell para su uso en redes cuánticas distribuidas de entrelazamiento. Aquí se proporciona una descripción técnica del protocolo de intercambio de entrelazamiento para estados Bell puros.

Alice y Bob preparan localmente conocido Los pares de Bell resultan en el estado inicial:
${displaystyle |psi rangle _{rm {in}}=|Phi ^{+}rangle _{A_{1},A_{2}}|Phi ^{+}rangle _{B_{1},B_{2}}}$
Alice envía qubit $A_1$ a un tercero Carol
Bob envía qubit ${displaystyle B_{1}}$ a Carol
Carol interpreta una proyección de Bell entre $A_{1}$ y $B_{1}$ que por casualidad resulta en el resultado de la medición:
${displaystyle langle Phi ^{+}|_{A_{1},B_{1}}|psi rangle _{rm {in}}=|Phi ^{+}rangle _{A_{2},B_{2}}}$
En el caso de los otros tres resultados de la proyección de Bell, las correcciones locales dadas por los operadores Pauli son hechas por Alice y Bob después de que Carol haya comunicado los resultados de la medición.
${displaystyle langle Phi ^{-}|_{A_{1},B_{1}}|psi rangle _{rm {in}}={hat {Z}}_{B_{2}}|Phi ^{+}rangle _{A_{2},B_{2}}}$
${displaystyle langle Psi ^{+}|_{A_{1},B_{1}}|psi rangle _{rm {in}}={hat {X}}_{B_{2}}|Phi ^{+}rangle _{A_{2},B_{2}}}$
${displaystyle langle Psi ^{-}|_{A_{1},B_{1}}|psi rangle _{rm {in}}={hat {X}}_{B_{2}}{hat {Z}}_{B_{2}}|Phi ^{+}rangle _{A_{2},B_{2}}}$
Alice y Bob ahora tienen un par de Bell entre cuartos $A_{2}$ y $B_{2}$
${displaystyle |psi rangle _{rm {out}}=|Phi ^{+}rangle _{A_{2},B_{2}}}$

Generalizaciones del protocolo de teletransportación

El protocolo de teletransportación básico para un qubit descrito anteriormente se ha generalizado en varias direcciones, en particular con respecto a la dimensión del sistema teletransportado y la cantidad de partes involucradas (ya sea como remitente, controlador o receptor).

Sistemas D-dimensionales

Una generalización $d$ - sistemas de nivel (llamados cuartos) es directo y ya fue discutido en el papel original por Bennett et al.: el estado máximo enredado de dos qubits tiene que ser reemplazado por un estado máximo enredado de dos cuartos y la medición de Bell por una medida definida por una base ortonormal máximamente enredada. Todas las generalizaciones posibles fueron discutidas por Werner en 2001. La generalización a los denominados sistemas infinitos y variables continuas se propuso en el primer experimento de teletransportación que funcionó incondicionalmente.

Versiones multipartitas

El uso de estados entrelazados multipartitos en lugar de un estado entrelazado máximo bipartito permite varias características nuevas: el remitente puede teletransportar información a varios receptores o enviar el mismo estado a todos ellos (lo que permite reducir la cantidad de entrelazamiento necesario para el proceso) o teletransportando estados multipartitos o enviando un solo estado de tal manera que las partes receptoras necesitan cooperar para extraer la información. Una forma diferente de ver la última configuración es que algunas de las partes pueden controlar si las otras pueden teletransportarse.

Teletransportación de puerta lógica

En general, se pueden transportar estados mixtos ρ y aplicar una transformación lineal ω durante la teletransportación, lo que permite el procesamiento de datos de información cuántica. Este es uno de los componentes básicos del procesamiento de información cuántica. Esto se demuestra a continuación.

Descripción general

Un esquema general de teletransportación se puede describir de la siguiente manera. Tres sistemas cuánticos están involucrados. El Sistema 1 es el estado (desconocido) ρ que será teletransportado por Alice. Los sistemas 2 y 3 están en un estado de enredo máximo ω que se distribuyen a Alice y Bob, respectivamente. El sistema total está entonces en el estado

rho otimes omega.

Un proceso de teletransportación exitoso es un canal cuántico LOCC Φ que satisface

(operatorname{Tr}_{12} circ Phi) (rho otimes omega) = rho,,

Donde Tr₁₂ es la operación de traza parcial con los sistemas de respeto 1 y 2, y $circ$ denota la composición de los mapas. Esto describe el canal en la imagen de Schrödinger.

Tomando mapas adjuntos en la imagen de Heisenberg, la condición de éxito se convierte en

langle Phi(rho otimes omega)| I otimes O rangle = langle rho | O rangle

para todos los observables O en el sistema de Bob. El factor tensor en $I otimes O$ es $12 otimes 3$ mientras que el de $rho otimes omega$ es $1 otimes 23$ .

Más detalles

El canal propuesto Φ se puede describir de manera más explícita. Para comenzar la teletransportación, Alice realiza una medición local en los dos subsistemas (1 y 2) que tiene en su poder. Suponga que la medición local tiene efectos

{F_i} = {M_i ^2}.

Si la medición registra el i-ésimo resultado, el estado general colapsa a

(M_i otimes I)(rho otimes omega)(M_i otimes I).

El factor tensor en $(M_i otimes I)$ es $12 otimes 3$ mientras que el de $rho otimes omega$ es $1 otimes 23$ . Bob entonces aplica una operación local correspondiente Ψ_i sobre el sistema 3. En el sistema combinado, esto se describe por

(Id otimes Psi_i)(M_i otimes I)(rho otimes omega)(M_i otimes I).

Donde Id es el mapa de identidad del sistema compuesto $1 otimes 2$ .

Por lo tanto, el canal Φ está definido por

Phi (rho otimes omega) = sum_i (Id otimes Psi_i)(M_i otimes I)(rho otimes omega)(M_i otimes I)

Aviso Φ cumple con la definición de LOCC. Como se indicó anteriormente, se dice que la teletransportación es exitosa si, para todos los O observables en el sistema de Bob, la igualdad

langle Phi(rho otimes omega), I otimes O rangle = langle rho, O rangle

espera. El lado izquierdo de la ecuación es:

sum_i langle (Id otimes Psi_i)(M_i otimes I)(rho otimes omega)(M_i otimes I), ; I otimes O rangle

= sum_i langle (M_i otimes I)(rho otimes omega)(M_i otimes I), ; I otimes Psi_i ^*(O)rangle

donde Ψ_i* es el adjunto de Ψ_i en la imagen de Heisenberg. Suponiendo que todos los objetos son de dimensión finita, esto se convierte en

sum_i operatorname{Tr} ; (rho otimes omega)(F_i otimes Psi_i^*(O)).

El criterio de éxito para la teletransportación tiene la expresión

sum_i operatorname{Tr} ; (rho otimes omega)(F_i otimes Psi_i ^*(O)) = operatorname{Tr} ; rho cdot O.

Explicación local del fenómeno

David Deutsch y Patrick Hayden presentan una explicación local de la teletransportación cuántica, con respecto a la interpretación de muchos mundos de la mecánica cuántica. Su artículo afirma que los dos bits que Alice le envía a Bob contienen "información localmente inaccesible" resultando en la teletransportación del estado cuántico. "La capacidad de la información cuántica para fluir a través de un canal clásico [...], sobreviviendo a la decoherencia, es [...] la base de la teletransportación cuántica."

Acontecimientos recientes

Si bien la teletransportación cuántica se encuentra en una etapa inicial, hay muchos aspectos relacionados con la teletransportación en los que los científicos están trabajando para comprender mejor o mejorar el proceso, que incluyen:

Dimensiones más altas

La teletransportación cuántica puede mejorar los errores asociados con el cálculo cuántico tolerante a fallas a través de una disposición de puertas lógicas. Los experimentos de D. Gottesman e I. L. Chuang han determinado que una "jerarquía de Clifford" Disposición de puerta que actúa para mejorar la protección contra errores ambientales. En general, se permite un umbral de error más alto con la jerarquía de Clifford ya que la secuencia de puertas requiere menos recursos de los necesarios para el cálculo. Si bien la mayor cantidad de puertas que se utilizan en una computadora cuántica crean más ruido, la disposición de las puertas y el uso de la teletransportación en la transferencia lógica pueden reducir este ruido, ya que requiere menos "tráfico". que se compila en estas redes cuánticas. Cuantos más qubits se utilizan para una computadora cuántica, más niveles se agregan a una disposición de puerta, y la diagonalización de la disposición de puerta varía en grado. El análisis de dimensiones superiores implica la disposición de puertas de nivel superior de la jerarquía de Clifford.

Calidad de la información

Teniendo en cuenta el requisito mencionado anteriormente de un estado entrelazado intermedio para la teletransportación cuántica, es necesario tener en cuenta la pureza de este estado para la calidad de la información. Una protección que se ha desarrollado implica el uso de información variable continua (en lugar de una variable discreta típica) creando un estado intermedio coherente superpuesto. Esto implica hacer un cambio de fase en la información recibida y luego agregar un paso de mezcla en la recepción utilizando un estado preferido, que podría ser un estado impar o incluso coherente, que estará "condicionado a la información clásica del remitente".; creando un estado de dos modos que contiene la información enviada originalmente.

También ha habido desarrollos con la teletransportación de información entre sistemas que ya tienen información cuántica en ellos. Experimentos realizados por Feng, Xu, Zhou et al. han demostrado que la teletransportación de un qubit a un fotón que ya tiene un qubit de información es posible gracias al uso de una puerta de entrelazamiento óptico qubit-ququart. Esta cualidad puede aumentar las posibilidades de cómputo, ya que se pueden realizar cálculos basados en información previamente almacenada, lo que permite mejorar los cálculos anteriores.

Contenido relacionado

Más resultados...