Susceptibilidad eléctrica

En la electricidad (electromagnetismo), el Susceptibilidad eléctrica ()${displaystyle chi _{e}}$; Latín: susceptibilis "receptivo") es una constante proporcionalidad sin dimensiones que indica el grado de polarización de un material dieléctrico en respuesta a un campo eléctrico aplicado. Cuanto mayor es la susceptibilidad eléctrica, mayor es la capacidad de un material para polarizar en respuesta al campo, y así reducir el campo eléctrico total dentro del material (y almacenar energía). Es de esta manera que la susceptibilidad eléctrica influye en la permitibilidad eléctrica del material y por lo tanto influye en muchos otros fenómenos en ese medio, desde la capacitancia de los condensadores hasta la velocidad de la luz.

Definición de dieléctricos lineales

Si un material dieléctrico es un dieléctrico lineal, entonces la susceptibilidad eléctrica se define como la constante de proporcionalidad (que puede ser una matriz) que relaciona un campo eléctrico E con la densidad de polarización dieléctrica inducida P tal que

$${displaystyle mathbf {P} = 'varepsilon ¿Por qué?$$

• ${displaystyle mathbf {P}$ es la densidad de polarización;
• ${displaystyle varepsilon ¿Qué?$ es la autorización eléctrica del espacio libre (continencia eléctrica);
• ${displaystyle chi _{e}}$ es la susceptibilidad eléctrica;
• ${displaystyle mathbf}$ es el campo eléctrico.

En materiales donde la susceptibilidad es anisotrópica (diferente según la dirección), la susceptibilidad se representa como una matriz conocida como tensor de susceptibilidad. Muchos dieléctricos lineales son isotrópicos, pero, no obstante, es posible que un material muestre un comportamiento que sea tanto lineal como anisotrópico, o que un material sea no lineal pero isotrópico. La susceptibilidad anisotrópica pero lineal es común en muchos cristales.

La susceptibilidad está relacionada con su relativa permitibilidad (constante dieléctrica) ${displaystyle varepsilon _{textrm {r}}$ por

$${displaystyle chi _{text{e} "varepsilon"$$

$${displaystyle chi _{text{e} =0.}$$

Al mismo tiempo, el desplazamiento eléctrico D está relacionado con la densidad de polarización P mediante la siguiente relación:

$${displaystyle mathbf {D} =varepsilon _{0}mathbf {E} +mathbf {P} =varepsilon _{0}(1+chi _{text{e})mathbf {E} =varepsilon ¿Por qué? _{0}mathbf {E} =varepsilon mathbf {E}$$

• ${displaystyle varepsilon =varepsilon ¿Por qué? ¿Qué?$
• ${displaystyle varepsilon _{text{r} = 1+chi _{text{e}}$

Polarizabilidad molecular

Existe un parámetro similar para relacionar la magnitud del momento de dipolo inducido p de una molécula individual al campo eléctrico local E que indujo la dipola. Este parámetro es el polarización molecular ()α), y el momento dipole resultante del campo eléctrico local E_local es dado por:

$${displaystyle mathbf {p} =varepsilon Alpha mathbf {Etext{local}}$$

Sin embargo, esto introduce una complicación, ya que localmente el campo puede diferir significativamente del campo aplicado en general. Tenemos:

$${displaystyle mathbf {P} =Nmathbf {p} =Nvarepsilon ¿Por qué? {E} _{text{local}}}$$

$${displaystyle chi _{text{e}mathbf {E} =Nalpha mathbf {E}{text{local}}$$

Así, sólo si el campo local es igual al campo ambiental podemos escribir:

$${displaystyle chi _{text{e}=Nalpha.}$$

De lo contrario, se debe encontrar una relación entre el campo local y el campo macroscópico. En algunos materiales, la relación Clausius–Mossotti mantiene y lee

$${displaystyle {frac {fnMicroc} {fnMicrosoft Sans Serif}{3+chi - ¿Qué? {Nalpha } {3}}$$

Ambigüedad en la definición

La definición de polarizabilidad molecular depende del autor. En la definición anterior,

$${displaystyle mathbf {p} =varepsilon Alpha mathbf {Etext{local}}}$$

${displaystyle p}$

${displaystyle E}$

${displaystyle alpha }$

${displaystyle varepsilon ¿Qué?$

${displaystyle alpha }$

$${displaystyle mathbf {p} =alpha mathbf {E_{text{local}}}}}$$

En esta segunda definición, la polarización tendría la unidad SI de C.m²/V. Existe otra definición donde ${displaystyle p}$ y ${displaystyle E}$ se expresan en el sistema cgs y ${displaystyle alpha }$ todavía se define como

$${displaystyle mathbf {p} =alpha mathbf {E_{text{local}}}}}$$

Usando las unidades de cgs ${displaystyle alpha }$ la dimensión de un volumen, como en la primera definición, pero con un valor que ${displaystyle 4pi}$ abajo.

Susceptibilidad no lineal

En muchos materiales, la polarizabilidad comienza a saturarse con valores altos de campo eléctrico. Esta saturación puede modelarse mediante una susceptibilidad no lineal. Estas susceptibilidades son importantes en la óptica no lineal y conducen a efectos como la generación de segundos armónicos (como los que se utilizan para convertir la luz infrarroja en luz visible, en los punteros láser verdes).

La definición estándar de susceptibilidades no lineales en unidades SI es mediante una expansión de Taylor de la reacción de polarización al campo eléctrico:

$${displaystyle P=P_{0}+varepsilon E+varepsilon ¿Por qué? ¿Qué?$$

${displaystyle P_{0}=0}$

${displaystyle chi ^{(1)}$

${displaystyle chi ^{(n)}$

Las susceptibilidades no lineales se pueden generalizar a materiales anisotrópicos en los que la susceptibilidad no es uniforme en todas las direcciones. En estos materiales, cada susceptibilidad ${displaystyle chi ^{(n)}$ se convierte en unn + 1Tensor de acuerdo.

Dispersión y causalidad

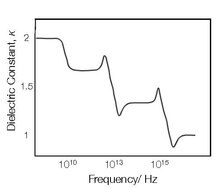
En general, un material no puede polarizarse instantáneamente en respuesta a un campo aplicado, por lo que la formulación más general como función del tiempo es

$${displaystyle mathbf {P} (t)=varepsilon _{0}int _{-infty }^{t}chi _{text{e}(t-t')mathbf {E} (t'),mathrm {d} t'.}$$

Es decir, la polarización es una convolución del campo eléctrico en tiempos anteriores con susceptibilidad dependiente del tiempo dada por ${displaystyle chi _{text{e} {Delta t)}$. El límite superior de esta integral puede extenderse al infinito también si se define ${displaystyle chi _{text{e} {Delta t)=0}$ para ${displaystyle Delta t won0}$. Una respuesta instantánea corresponde a la susceptibilidad de la función Dirac delta ${displaystyle chi _{text{e} {Delta t)=chi _{text{e}delta (Delta t)}$.

Es más conveniente en un sistema lineal tomar la transformada de Fourier y escribir esta relación como una función de la frecuencia. Debido al teorema de convolución, la integral se convierte en un producto,

$${displaystyle mathbf {P} (omega)=varepsilon _{0}chi _{text{e} {omega)mathbf {E} (omega). }$$

Esto tiene una forma similar a la relación Clausius-Mossotti:

$${displaystyle mathbf {P} (mathbf {r})=varepsilon ¿Qué? {Nalpha (mathbf {r}}{1-{frac {1}{3}N(mathbf {r})alpha (mathbf {r})}mathbf {E} (mathbf {r})=varepsilon _{0}chi _{text{e}(mathbf {r}))mathbf {E} (mathbf} {} {} {} {} {} {} {}} {}}} {}} {} {} {}}} {}}}} {} {} {} {}}}} {})} {} {}} {} {})} {} {} {}}}}}}}}} {}}}}}}} {} {})} {}}} {} {}} {} {} {}}}} {} {}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}}}}$$

Esta dependencia de la frecuencia de la susceptibilidad conduce a la dependencia de la frecuencia de la permitividad. La forma de la susceptibilidad con respecto a la frecuencia caracteriza las propiedades de dispersión del material.

Además, el hecho de que la polarización sólo puede depender del campo eléctrico en tiempos anteriores (es decir,. ${displaystyle chi _{text{e} {Delta t)=0}$ para ${displaystyle Delta t won0}$), una consecuencia de la causalidad, impone restricciones Kramers-Kronig a la susceptibilidad ${displaystyle chi _{text{e}(0)}$.