Sumador de anticipación

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Circuito lógico Aritmético

Un sumador de anticipación (CLA) o un sumador rápido es un tipo de sumador electrónico utilizado en lógica digital. Un sumador de anticipación de acarreo mejora la velocidad al reducir la cantidad de tiempo necesario para determinar los bits de acarreo. Se puede contrastar con el sumador de acarreo rizado (RCA), más simple, pero generalmente más lento, para el cual el bit de acarreo se calcula junto con el bit de suma, y cada etapa debe esperar hasta que se haya calculado el bit de acarreo anterior para comenzar a calcular el suyo propio. bit de suma y bit de acarreo. El sumador de anticipación de acarreo calcula uno o más bits de acarreo antes de la suma, lo que reduce el tiempo de espera para calcular el resultado de los bits de mayor valor del sumador.

Ya a mediados del siglo XIX, Charles Babbage reconoció la penalización en el rendimiento impuesta por el transporte de ondas utilizado en su motor diferencial y posteriormente diseñó mecanismos para anticipar el transporte para su motor analítico nunca construido. Se cree que Konrad Zuse implementó el primer sumador de anticipación en su computadora mecánica binaria de la década de 1930, la Zuse Z1. Gerald B. Rosenberger de IBM solicitó una patente sobre un moderno sumador binario de anticipación en 1957.

Dos implementaciones ampliamente utilizadas del concepto son el sumador Kogge-Stone (KSA) y el sumador Brent-Kung (BKA).

Teoría del funcionamiento

Adición de ondas

Un sumador binario de ondulación y acarreo funciona de la misma manera que la mayoría de los métodos de suma de lápiz y papel. Comenzando en la posición del dígito más a la derecha (menos significativa), se suman los dos dígitos correspondientes y se obtiene un resultado. Un 'realizar' puede ocurrir si el resultado requiere un dígito más alto; por ejemplo, "9 + 5 = 4, lleva 1". La aritmética binaria funciona de la misma manera, con menos dígitos. En este caso, sólo hay cuatro operaciones posibles, 0+0, 0+1, 1+0 y 1+1; el caso 1+1 genera un acarreo. En consecuencia, todas las posiciones de los dígitos, excepto la que está más a la derecha, deben esperar la posibilidad de tener que agregar un 1 adicional al llevar los dígitos una posición a la derecha.

Esto significa que ninguna posición de dígito puede tener un valor absolutamente final hasta que se haya establecido si un acarreo viene o no desde la derecha. Además, si la suma sin acarreo es el valor más alto en la base (9 en los métodos de lápiz y papel en base 10 o 1 en aritmética binaria), no es posible saber si una posición dada de un dígito va a cambiar o no. pasar un acarreo a la posición a su izquierda. En el peor de los casos, cuando toda una secuencia de sumas llega a …99999999… (en decimal) o …11111111… (en binario), no se puede deducir nada en absoluto hasta que se conozca el valor del acarreo que entra por la derecha; ese acarreo debe propagarse hacia la izquierda, un paso a la vez, ya que la posición de cada dígito evalúa "9 + 1 = 0, acarreo 1" o "1 + 1 = 0, lleva 1". Es la "ondulación" del acarreo de derecha a izquierda que le da al sumador de acarreo ondulado su nombre y lentitud. Al sumar enteros de 32 bits, por ejemplo, se debe tener en cuenta la posibilidad de que un acarreo tenga que propagarse a través de cada uno de los 32 sumadores de un bit.

Anticipación

El carry-lookahead depende de dos cosas:

Calculando para cada posición de dígito si esa posición va a propagar un port si uno viene de la derecha.
Combinando estos valores calculados para poder deducir rápidamente si, para cada grupo de dígitos, ese grupo va a propagar una carga que viene de la derecha.

Suponiendo que se eligen grupos de cuatro dígitos. La secuencia de eventos sería así:

Todos los adders de 1 bit calculan sus resultados. Simultáneamente, las unidades de cabeza de mira realizan sus cálculos.
Asumiendo que una carga surja en un grupo particular, que porta surgirá en el extremo izquierdo del grupo dentro de la mayoría de cinco demoras de la puerta y empezará a propagarse a través del grupo a su izquierda.
Si ese porte va a propagar todo el camino a través del próximo grupo, la unidad de miradores ya habrá deducido esto. En consecuencia, antes de que la carga emerge del siguiente grupo, la unidad de cabeza de mira es inmediatamente (dentro de una puerta de retraso) capaz de decir siguiente grupo a la izquierda que va a recibir una carga – y, al mismo tiempo, para decirle a la siguiente unidad de cabeza a la izquierda que una carga está en camino.

El efecto neto es que los acarreos comienzan propagándose lentamente a través de cada grupo de 4 bits, tal como en un sistema de acarreo continuo, pero luego se mueven cuatro veces más rápido, saltando de una unidad de acarreo anticipado a la siguiente. Finalmente, dentro de cada grupo que recibe un acarreo, el acarreo se propaga lentamente dentro de los dígitos de ese grupo.

Cuantos más bits haya en un grupo, más compleja se vuelve la lógica de acarreo anticipado y más tiempo se dedica a las "vías lentas" en cada grupo en lugar de en la "vía rápida" entre los grupos (proporcionado por la lógica de acarreo anticipado). Por otro lado, cuantos menos bits haya en un grupo, más grupos habrá que atravesar para llegar de un extremo al otro de un número y, como resultado, se obtendrá menos aceleración.

Decidir que el tamaño del grupo se regirá por la lógica de acarreo anticipado requiere un análisis detallado de los retrasos de puerta y propagación para la tecnología particular que se utiliza.

Es posible tener más de un nivel de lógica de anticipación y acarreo y, de hecho, esto se suele hacer. Cada unidad de acarreo anticipado ya produce una señal que dice "si un acarreo llega desde la derecha, lo propagaré hacia la izquierda", y esas señales se pueden combinar de modo que cada grupo de, digamos, cuatro unidades de acarreo anticipado -las unidades de transporte pasan a formar parte de un "supergrupo" que rige un total de 16 bits de los números que se van sumando. El "supergrupo" La lógica de acarreo anticipado podrá decir si un acarreo que ingresa al supergrupo se propagará a través de él y, utilizando esta información, puede propagar acarreos de derecha a izquierda 16 veces más rápido que un acarreo ingenuo. Con este tipo de implementación de dos niveles, un acarreo puede propagarse primero a través del "camino lento" de sumadores individuales, luego, al llegar al extremo izquierdo de su grupo, se propagan a través de la "vía rápida" de lógica de acarreo anticipado de 4 bits, luego, al llegar al extremo izquierdo de su supergrupo, se propaga a través de la "carretera superrápida" de lógica de acarreo anticipado de 16 bits.

Nuevamente, los tamaños de grupo que se elegirán dependen de los detalles exactos de qué tan rápido se propagan las señales dentro de las puertas lógicas y de una puerta lógica a otra.

Para números muy grandes (cientos o incluso miles de bits), la lógica de acarreo anticipado no se vuelve más compleja, porque se pueden agregar más capas de supergrupos y supersupergrupos según sea necesario. El aumento en el número de puertas también es moderado: si todos los tamaños de grupo son cuatro, uno terminaría con un tercio de unidades de acarreo anticipado que sumadores. Sin embargo, los "caminos lentos" en el camino hacia niveles más rápidos comienzan a imponer un lastre a todo el sistema (por ejemplo, un sumador de 256 bits podría tener hasta 24 retrasos de puerta en su procesamiento de acarreo), y la mera transmisión física de señales desde un extremo de un El número largo para el otro comienza a ser un problema. En estos tamaños, son preferibles los sumadores de ahorro de acarreo, ya que no dedican ningún tiempo a la propagación del acarreo.

Llevar el método de anticipación

La lógica de anticipación del acarreo utiliza los conceptos de generar y propagar acarreos. Aunque en el contexto de un sumador con anticipación, lo más natural es pensar en generar y propagar en el contexto de la suma binaria, los conceptos se pueden usar de manera más general. En las descripciones siguientes, la palabra dígito se puede reemplazar por bit cuando se hace referencia a la suma binaria de 2.

Se dice que la suma de dos entradas de 1 dígito A y B genera si la suma siempre se llevará a cabo, independientemente de si hay es un acarreo de entrada (de manera equivalente, independientemente de si se acarrean dígitos menos significativos en la suma). Por ejemplo, en la suma decimal 52 + 67, la suma de los dígitos de las decenas 5 y 6 genera porque el resultado se lleva al dígito de las centenas independientemente de si el dígito de las unidades lleva; en el ejemplo, el dígito de las unidades no lleva (2 + 7 = 9). Incluso si los números fueran, digamos, 54 y 69, la suma de los dígitos de las decenas 5 y 6 seguiría generando porque el resultado una vez más llega al dígito de las centenas a pesar de que 4 y 9 crean un acarreo.

En el caso de adición binaria, ${displaystyle A+B}$ genera si y sólo si ambos A y B son 1. Si escribimos ${displaystyle G(A,B)}$ para representar el predicado binario que es verdad si y sólo si ${displaystyle A+B}$ genera, tenemos

{displaystyle G(A,B)=Acdot B}

Donde ${displaystyle Acdot B}$ es una conjunción lógica (es decir, una y).

Se dice que la suma de dos entradas de 1 dígito A y B se propaga si la suma se llevará siempre que haya un acarreo de entrada. (de manera equivalente, cuando lleva el siguiente dígito menos significativo de la suma). Por ejemplo, en la suma decimal 37 + 62, la suma de los dígitos de las decenas 3 y 6 se propaga porque el resultado se trasladaría al dígito de las centenas si las unidades llevaran (que en este ejemplo no es así). Tenga en cuenta que propagar y generar se definen con respecto a un solo dígito de la suma y no dependen de ningún otro dígito en la suma.

En el caso de adición binaria, ${displaystyle A+B}$ propaga si y sólo si al menos uno de A o B 1. Si ${displaystyle P(A,B)}$ está escrito para representar el predicado binario que es verdad si y sólo si ${displaystyle A+B}$ propaga, uno tiene

{displaystyle P(A,B)=A+B}

Donde ${displaystyle A+B}$ en el lado derecho de la ecuación es una disyunción lógica (es decir, una o).

A veces se utiliza una definición ligeramente diferente de propagar. Según esta definición, se dice que A + B se propaga si la suma se transportará siempre que haya un acarreo de entrada, pero no se propagará si no hay acarreo de entrada. Debido a la forma en que la lógica de anticipación de acarreo utiliza los bits de generación y propagación, no importa qué definición se utilice. En el caso de la suma binaria, esta definición se expresa por

{displaystyle P'(A,B)=Aoplus B}

Donde ${displaystyle Aoplus B}$ es una exclusiva o (es decir, una xor).

${displaystyle A}$	${displaystyle B}$	${displaystyle C_{i}}$	${displaystyle C_{o}}$	Tipo de Carry
0	0	0	0	Ninguno
0	0	1	0	Ninguno
0	1	0	0	Ninguno
0	1	1	1	Propagado
1	0	0	0	Ninguno
1	0	1	1	Propagado
1	1	0	1	Generar
1	1	1	1	Generar/Propagate

Tabla que muestra cuándo se propagan o generan acarreos.

Para aritmética binaria, o es más rápido que xor y necesita menos transistores para implementar. Sin embargo, para una escalerilla de lookahead de múltiples niveles, es más sencillo utilizar ${displaystyle P'(A,B)}$ .

Dados estos conceptos de generación y propagación, un dígito de adición lleva precisamente cuando la adición genera o el siguiente bit menos significativo lleva y la adición se propaga. Escrito en álgebra booleana, con ${displaystyle C_{i}}$ el bit de carga del dígito i, y ${displaystyle P_{i}}$ y ${displaystyle G_{i}}$ el propagar y generar bits de dígitos i respectivamente

{displaystyle C_{i+1}=G_{i}+(P_{i}cdot C_{i}).}

Detalles de implementación

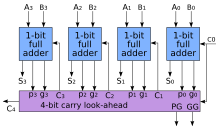
Para cada bit en una secuencia binaria que se agregue, la lógica de anticipación del acarreo determinará si ese par de bits generará un acarreo o propagará un acarreo. Esto permite que el circuito "preprocesar" Los dos números se suman para determinar el acarreo con anticipación. Luego, cuando se realiza la suma real, no hay demora por esperar el efecto de acarreo dominó (o el tiempo que tarda el acarreo desde el primer sumador completo en pasar al último sumador completo).

Para determinar si un par de bits generará un acarreo, funciona la siguiente lógica:

{displaystyle G_{i}=A_{i}cdot B_{i}}

Para determinar si un par de bits propagará una carga, cualquiera de las siguientes declaraciones lógicas funcionan:

{displaystyle P_{i}=A_{i}oplus B_{i}}

{displaystyle P_{i}=A_{i}+B_{i}}

La razón por la cual este trabajo se basa en la evaluación de ${displaystyle C_{1}=G_{0}+P_{0}cdot C_{0}}$ . La única diferencia en las tablas de verdad entre ( ${displaystyle Aoplus B}$ ) y ( ${displaystyle A+B}$ ) es cuando ambos ${displaystyle A}$ y ${displaystyle B}$ son 1. Sin embargo, si ambos ${displaystyle A}$ y ${displaystyle B}$ son 1, entonces el ${displaystyle G_{0}}$ término es 1 (ya que su ecuación es ${displaystyle Acdot B}$ ), y el ${displaystyle P_{0}cdot C_{0}}$ el término se vuelve irrelevante. El XOR se utiliza normalmente dentro de un circuito de escalera completa básico; el OR es una opción alternativa (sólo para un port-lookahead), que es mucho más simple en términos de cuenta de transistor.

Por ejemplo, la lógica para la generación ( ${displaystyle G}$ ) y propagar ( ${displaystyle P}$ ) valores se dan a continuación. El valor numérico determina la señal desde el circuito anterior, a partir de 0 en la extrema derecha a 3 en la izquierda:

{displaystyle C_{1}=G_{0}+P_{0}cdot C_{0}}

{displaystyle C_{2}=G_{1}+P_{1}cdot C_{1}}

{displaystyle C_{3}=G_{2}+P_{2}cdot C_{2}}

{displaystyle C_{4}=G_{3}+P_{3}cdot C_{3}}

Sustitución ${displaystyle C_{1}}$ en ${displaystyle C_{2}}$ Entonces ${displaystyle C_{2}}$ en ${displaystyle C_{3}}$ Entonces ${displaystyle C_{3}}$ en ${displaystyle C_{4}}$ produce las siguientes ecuaciones ampliadas:

{displaystyle C_{1}=G_{0}+P_{0}cdot C_{0}}

{displaystyle C_{2}=G_{1}+G_{0}cdot P_{1}+C_{0}cdot P_{0}cdot P_{1}}

{displaystyle C_{3}=G_{2}+G_{1}cdot P_{2}+G_{0}cdot P_{1}cdot P_{2}+C_{0}cdot P_{0}cdot P_{1}cdot P_{2}}

{displaystyle C_{4}=G_{3}+G_{2}cdot P_{3}+G_{1}cdot P_{2}cdot P_{3}+G_{0}cdot P_{1}cdot P_{2}cdot P_{3}+C_{0}cdot P_{0}cdot P_{1}cdot P_{2}cdot P_{3}}

La escalerilla de 4 bits de lookahead también se puede utilizar en un circuito de alto nivel al tener cada circuito lógico CLA producir una señal propagada y generar a un circuito lógico CLA de alto nivel. El grupo se propaga ( ${displaystyle PG}$ ) y grupo generar ( ${displaystyle GG}$ ) para un CLA de 4 bits son:

{displaystyle PG=P_{0}cdot P_{1}cdot P_{2}cdot P_{3}}

{displaystyle GG=G_{3}+G_{2}cdot P_{3}+G_{1}cdot P_{3}cdot P_{2}+G_{0}cdot P_{3}cdot P_{2}cdot P_{1}}

Luego se pueden utilizar para crear una transferencia para ese grupo de 4 bits en particular:

{displaystyle CG=GG+PGcdot C_{in}}

Se puede ver que esto es equivalente a ${displaystyle C_{4}}$ en ecuaciones anteriores.

La juntación de cuatro CLA de 4 bits produce cuatro grupos propaga y cuatro grupos genera. Una unidad Lookahead-carry (LCU) toma estos 8 valores y utiliza la lógica idéntica para calcular ${displaystyle C_{i}}$ en los CLA. La LCU genera entonces la entrada de carga para cada uno de los 4 CLA y un quinto igual a ${displaystyle C_{16}}$ .

El cálculo del retardo de puerta de un sumador de 16 bits (que utiliza 4 CLA y 1 LCU) no es tan sencillo como el del sumador de acarreo rizado.

A partir del momento cero:

cálculo ${displaystyle P_{i}}$ y ${displaystyle G_{i}}$ se hace a la vez 1,
cálculo del ${displaystyle PG}$ se hace a la vez 2,
cálculo del ${displaystyle GG}$ se hace a la vez 3,
El cálculo de los insumos para los CLA de la LCU se hace en:
- tiempo 0 para el primer CLA,
- tiempo 5 para la segunda, tercera y cuarta CLA,
cálculo del Si{displaystyle S_{i} ${displaystyle S_{i}}$ se hacen en:
- tiempo 4 para la primera CLA,
- tiempo 8 para la segunda, tercera y cuarta CLA,
cálculo del bit de carga final ( ${displaystyle C_{16}}$ ) se hace a la hora 5.

El tiempo máximo es 8 demoras de la puerta (para ${displaystyle S_{[8-15]}}$ ).

Una escalera estándar de 16 bits de carga ondulada tomaría 16 × 2 − 1 = 31 retrasos de la puerta.

Expansión

Este ejemplo es un sumador anticipado de acarreo de 4 bits, hay 5 salidas. A continuación se muestra la expansión:

S0 = (A0 XOR B0) XOR Cin '2dt (dt - tiempo de demora)

S1 = (A1 XOR B1)
XOR (A0 Y B0)
O (A0 XOR B0) Y Cin) '4dt

S2 = (A2 XOR B2)
XOR (A1 y B1)
O (A1 XOR B1) Y (A0 Y B0)
OR (A1 XOR B1) AND (A0 XOR B0) AND Cin) '4dt

S3 = (A3 XOR B3)
XOR (A2 y B2)
OR (A2 XOR B2) AND (A1 AND B1))
OR (A2 XOR B2) AND (A1 XOR B1) AND (A0 AND B0))
OR (A2 XOR B2) AND (A1 XOR B1) AND (A0 XOR B0) AND Cin)) '4dt

Cout = (A3 y B3)
OR (A3 XOR B3) AND (A2 AND B2))
OR (A3 XOR B3) AND (A2 XOR B2) AND (A1 AND B1))
OR (A3 XOR B3) AND (A2 XOR B2) AND (A1 XOR B1) AND (A0 AND B0))
OR (A3 XOR B3) AND (A2 XOR B2) AND (A1 XOR B1) AND (A0 XOR B0) AND Cin) '3dt

Sumador de anticipación de acarreo de 4 bits más simple:

Paso 0
Gin = Cin '0dt
P00 = A0 XOR B0 '1dt
G00 = A0 Y B0 '1dt
P10 = A1 XOR B1 '1dt
G10 = A1 y B1
P20 = A2 XOR B2 '1dt
G20 = A2 y B2 '1dt
P30 = A3 XOR B3 '1dt
G30 = A3 y B3 '1dt
Paso 1
G01 = G00 OR_
P00 Y Gin '3dt, C0, valency-2
G11 = G10 OR_
P10 y G00 OR_
P10 Y P00 Y Gin '3dt, C1, valency-3
G21 = G20 OR_
P20 y G10 OR_
P20 y P10 y G00 OR_
P20 y P10 y P00 y Gin '3dt, C2, valency-4
G31 = G30 OR_
P30 y G20 OR_
P30 y P20 y G10 OR_
P30 y P20 y P10 y G00 OR_
P30 y P20 y P10 y P00 y Gin '3dt, C3, valency-5
'Sum
S0 = P00 XOR Gin '2dt
S1 = P10 XOR G01 '4dt
S2 = P20 XOR G11 '4dt
S3 = P30 XOR G21 '4dt
S4 = G31 '3dt, Cout

Cadena de transporte Manchester

La cadena de acarreo de Manchester es una variación del sumador de acarreo anticipado que utiliza lógica compartida para reducir el recuento de transistores. Como se puede ver arriba en la sección de implementación, la lógica para generar cada acarreo contiene toda la lógica utilizada para generar los acarreos anteriores. Una cadena de acarreo de Manchester genera acarreos intermedios desconectando nodos en la puerta que calcula el valor de acarreo más significativo. Sin embargo, no todas las familias lógicas tienen estos nodos internos, siendo CMOS un ejemplo importante. La lógica dinámica puede admitir la lógica compartida, al igual que la lógica de la puerta de transmisión. Una de las principales desventajas de la cadena de acarreo de Manchester es que la carga capacitiva de todas estas salidas, junto con la resistencia de los transistores, hace que el retraso de propagación aumente mucho más rápidamente que una anticipación de acarreo normal. Una sección de la cadena de transporte Manchester generalmente no supera los 4 bits.

Más resultados...