Subtangente

En geometría, la subtangente y términos relacionados son ciertos segmentos de línea definidos usando la línea tangente a una curva en un punto dado y los ejes de coordenadas. Los términos son algo arcaicos hoy en día, pero fueron de uso común hasta principios del siglo XX.

Definiciones

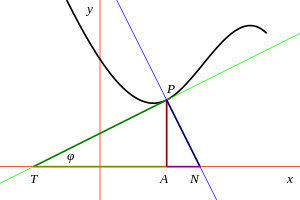
Sea P = (x, y) un punto en una curva dada con A = (x, 0) su proyección sobre el eje x. Dibuja la tangente a la curva en P y deja que T sea el punto donde esta línea cruza el eje x. Entonces TA se define como la subtangente en P. De manera similar, si la normal a la curva en P intersecta el eje x en N, entonces AN se llama subnormal. En este contexto, las longitudes PT y PN se denominan tangente y normal, y no deben confundirse con las recta tangente y recta normal, que también se llaman tangente y normal.

Ecuaciones

Sea φ el ángulo de inclinación de la tangente con respecto al eje x; esto también se conoce como ángulo tangencial. Entonces

#⁡ ⁡ φ φ =dSí.dx=APTA=ANAP.{displaystyle tan varphi ={frac {y} {dx}={frac} {}= {fn} {fnK}} {fnK}} {fnMicroc {fn}} {fn} {fnK}}} {fnK}} {fnK}}} {fnK}} {fnK}} {f}}} {fnKf}}}}} {f}}}}}}}}}}} {f}}}}}}} {f}}}}}}}}} {f} {f}}}} {f}} {f}}}}}}}}}}}}}}}}}}}} {f}}}}} {f}} {f}}} {f}}}} {f}}} {f}}}}}}f}}}}}}}}}} {f}}}fnKf}}fnKf}fnKf}}}fn

Entonces la subtangente es

Sí.cot⁡ ⁡ φ φ =Sí.dSí.dx,{displaystyle ycot varphi {fnMicroc} {fnMicroc} {y} {dx}}}}

y lo subnormal es

Sí.#⁡ ⁡ φ φ =Sí.dSí.dx.{displaystyle ytan varphi =y{frac {y} {dx}}}

La normal está dada por

Sí.sec⁡ ⁡ φ φ =Sí.1+()dSí.dx)2,{displaystyle ysec varphi - Sí.

y la tangente está dada por

Sí.csc⁡ ⁡ φ φ =Sí.dSí.dx1+()dSí.dx)2.{displaystyle ycsc varphi {fnMicroc} {fnMicroc} {y} {dx} {fn} {fnK}} {fn}} {fn} {fn}} {fn}} {fn}} {fn}}} {fn}}}} {fn}}} {f}}} {f}}}}} {f}}}}}} {f}}}}} {f}}}}}}}}}}}}} {f}}}}}}}} {f}}}} {f}}}}} {f}}}}} {f}}}} {f}}}}}}}}} {f}}}} {f}}}}}}}}} {f}}} {f}}}} {f}}} {f}}}} {f}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}} {1+left {fnMicroc}}} {2}}}

Definiciones polares

Sea P = (r, θ) un punto en una curva dada definida por coordenadas polares y sea O el origen. Dibuje una línea que pase por O que sea perpendicular a OP y sea ahora T el punto donde esta línea corta la tangente a la curva en P. De manera similar, sea ahora N el punto donde la normal a la curva intersecta la línea. Entonces OT y ON se denominan, respectivamente, subtangente polar y subnormal polar de la curva en . P.

Ecuaciones polares

Sea ψ el ángulo entre la tangente y el rayo OP; esto también se conoce como ángulo tangencial polar. Entonces

#⁡ ⁡ ↑ ↑ =rdrdSilencio Silencio =OPON=OTOP.{displaystyle tan psi {fnMicroc} {fnMicroc} {d}{dtheta ¿Qué?

Entonces la subtangente polar es

r#⁡ ⁡ ↑ ↑ =r2drdSilencio Silencio ,{displaystyle rtan psi {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}} {fnMicroc} {dr} {dtheta}}}}

y lo subnormal es

rcot⁡ ⁡ ↑ ↑ =drdSilencio Silencio .{displaystyle rcot psi ={frac {d}{dtheta }}