SRGB
sRGB es un espacio de color RGB (rojo, verde, azul) estándar que HP y Microsoft crearon en colaboración en 1996 para utilizar en monitores, impresoras y la World Wide Web. Posteriormente fue estandarizado por la Comisión Electrotécnica Internacional (IEC) como IEC 61966-2-1:1999. sRGB es el espacio de color estándar definido actualmente para la web y, por lo general, es el espacio de color asumido para imágenes que no están etiquetadas para un espacio de color ni tienen un perfil de color incorporado.
sRGB esencialmente codifica las especificaciones de visualización de los monitores de computadora en uso en ese momento, lo que contribuyó enormemente a su aceptación. sRGB utiliza los mismos colores primarios y punto blanco que el estándar ITU-R BT.709 para HDTV, una función de transferencia (o gamma) compatible con las pantallas CRT de la época y un entorno de visualización diseñado para igualar la visualización típica en el hogar y la oficina. condiciones.
Definición
Gama
| Cromaticidad | Rojo | Verde | Azul | Punto blanco |
|---|---|---|---|---|
| x | 0,6400 | 0,3000 | 0.1500 | 0,3127 |
| Sí. | 0,3300 | 0.6000 | 0,0600 | 0,3290 |
| Y | 0.2126 | 0,75152 | 0,0722 | 1.0000 |
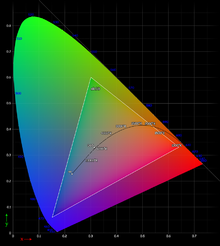
sRGB define las cromaticidades de las primarías rojas, verdes y azules, los colores donde uno de los tres canales es no cero y los otros dos son cero. La gama de cromaticidades que se pueden representar en sRGB es el triángulo de color definido por estas primarias, que se establecen tal que la gama de colores dentro del triángulo está bien dentro de la gama de colores visibles a un humano con visión tricromática normal. Como con cualquier espacio de color RGB, para valores no negativos de R, G y B no es posible representar colores fuera de este triángulo.
Las primarias provienen de HDTV (ITU-R BT.709), que son algo diferente de las de los sistemas de televisión de color más antiguos (ITU-R BT.601). Estos valores fueron elegidos para reflejar el color aproximado de los fosforos CRT de consumo en el momento de su diseño. Dado que las pantallas planas en ese momento estaban diseñadas generalmente para emular las características de la TRC, los valores también reflejaban la práctica imperante para otros dispositivos de visualización.
Función de transferencia ("gamma")


La especificación IEC indica una pantalla de referencia con una gamma nominal de 2,2, que el grupo de trabajo sRGB determinó que era representativa de los CRT utilizados con los sistemas operativos Windows en ese momento. La capacidad de mostrar imágenes sRGB directamente en un CRT sin necesidad de realizar ninguna búsqueda ayudó enormemente a la adopción de sRGB. Gamma también codifica de manera útil más datos cerca del negro, lo que reduce el ruido visible y los artefactos de cuantificación.
El estándar define además una función de transferencia optoelectrónica (OETF), que define la conversión de la luz lineal o la intensidad de la señal a los datos de imagen comprimida por gamma. Esta curva es aproximadamente el inverso de la pantalla γ γ 2.2{displaystyle gamma ^{2.2}, pero con algunos ajustes para evitar una pendiente infinita a cero. Cerca de cero, a γ γ 1/2.4{displaystyle gamma ^{1/2.4} curva de potencia intercepta una sección de línea recta que conduce a cero. Esto evita la pendiente infinita a cero que ocurriría si se utilizara una curva de potencia simple.
En la práctica un puro γ γ 2.2{displaystyle gamma ^{2.2} puede ser utilizado con datos sRGB con muy poca diferencia. Esto mejora el rendimiento computacional y se conoce como "simple sRGB" por Adobe, Esto es también cómo la mayoría de las pantallas transforman los datos de imagen codificados a la pantalla.
Computing the transfer function
Una línea recta que pasa por (0,0) es Sí.=xCCPR CCPR {displaystyle y={frac {x} {fn}}, y una curva gamma que pasa a través (1,1) es Sí.=()x+A1+A). . {displaystyle y=left({frac {x+A}{1+A}derecho)}
Si estos se unen en el punto (X,X/Φ) entonces:
- XCCPR CCPR =()X+A1+A). . {displaystyle {frac {fnK}=left({frac {X+A}{1+A}right)}{Gamma }}}
Para evitar un punto donde los dos segmentos se encuentran, las derivadas deben ser iguales en este punto:
- 1CCPR CCPR =. . ()X+A1+A). . − − 1()11+A){displaystyle {frac {1}{Phi}}=Gammaleft({frac {X+A}{1+A}}right)}{Gamma -1}left({frac {1}{1+A}right)}}}}}
Ahora tenemos dos ecuaciones. Si tomamos las dos incógnitas como X y Φ entonces podemos resolver dar
- X=A. . − − 1,CCPR CCPR =()1+A). . (). . − − 1). . − − 1()A. . − − 1)(). . . . ){displaystyle X={frac {A}{Gamma -1}}Phi ={frac {(1+A)^{Gamma }(Gamma -1)^{ Gamma - ¿Qué? ¿Qué?
Los valores A = 0,055 y Γ = 2,4 se eligieron para que la curva se pareciera mucho la curva gamma-2.2. Esto da X ≈ 0.0392857, Φ ≈ 12.9232102. Estos valores, redondeados a X = 0,03928, Φ = 12,92321 a veces describen la conversión sRGB.
Los borradores de las publicaciones de los creadores de sRGB redondearon aún más Φ = 12,92, lo que resultó en una pequeña discontinuidad en la curva. Algunos autores adoptaron estos valores incorrectos, en parte porque el borrador estaba disponible gratuitamente y el estándar oficial IEC está detrás de un muro de pago. Para el estándar, se mantuvo el valor redondeado de Φ y se volvió a calcular X como 0.04045 para hacer que la curva sea continua, lo que resulta en una discontinuidad de pendiente desde 1/12.92 debajo de la intersección hasta 1/12.70 arriba.
Entorno de visualización
| Parámetro | Valor |
|---|---|
| Nivel de iluminación de pantalla | 80 cd/m2 |
| Punto blanco iluminado | x = 0,3127, Sí. = 0,3290 (D65) |
| Reflexión envolvente de imagen | 20% (~medio gris) |
| Nivel de iluminación ambiental | 64 lux |
| Codificación de punto blanco ambiente | x = 0,3457, Sí. = 0,3585 (D50) |
| Codificación visual | 1.0% |
| Nivel típico de iluminación ambiental | 200 lux |
| Típico punto blanco ambiente | x = 0,3457, Sí. = 0,3585 (D50) |
| Típica bengala de visión | 5.0% |
La especificación sRGB asume un ambiente de codificación (creación) dimly encendido con una temperatura de color relacionada con el ambiente (CCT) de 5003 K. Esto difiere del CCT del iluminante (D65). Usar D50 para ambos habría hecho que el punto blanco de la mayoría de papel fotográfico parezca excesivamente azul. Los otros parámetros, como el nivel de luminancia, son representativos de un monitor CRT típico.
Para obtener resultados óptimos, el ICC recomienda utilizar el entorno de visualización de codificación (es decir, dim, iluminación difusa) en lugar del entorno de visualización típico menos exigente.
Transformación
De sRGB a CIE XYZ
Valores del componente SRGB Rsrgb{displaystyle R_{mathrm {srgb}, Gsrgb{displaystyle G_{mathrm {srgb}, Bsrgb{displaystyle B_{mathrm {srgb} están en el rango 0 a 1. Cuando se representa digitalmente como números de 8 bits, estos valores de componentes de color están en el rango de 0 a 255, y debe dividirse (en una representación de punto flotante) por 255 para convertir a la gama de 0 a 1.
- 0.04045end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">Clinear={}Csrgb12.92,Csrgb≤ ≤ 0,04045()Csrgb+0,0551.055)2.4,Csrgb■0,04045{displaystyle C_{mathrm {linear} {begin{cases}{dfrac {C_{mathrm {srgb}} {12.92}}}}} {C_{mathrm {srgb}leq 0.04045[5mu]left({dfrac {C_{mathrm {srgb} }+0.055}{1.055}}}right)}{2.4} {mccccc}
0.04045end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert skin-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1cedac5578c8ba045e7ed1f4a4c5f760adcb7722" style="vertical-align: -6.005ex; width:49.711ex; height:13.176ex;"/>
Donde C{displaystyle C} es R{displaystyle R., G{displaystyle G.o B{displaystyle B}.
Estos valores de gamma-expanded (a veces llamados "valores lineales" o "valores de luz lineal") se multiplican por una matriz para obtener CIE XYZ (la matriz tiene precisión infinita, cualquier cambio en sus valores o añadir no-ceros no se permite):
- [XD65YD65ZD65]=[0.41240,35760.18050.21260,751520,07220,01930.11920.9505][RlinealGlinealBlineal]{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {b}fnMicrosoft Sans Serif}} {b}f}b}b}b}b}b}b}b}b}b}b}b}bb}b}b}bcH0cH0}cH0}b}bbb}bb}bbb}cH0}cH0}b}cH0cH0cH0cH0cH0}cH0}cH0cH0cH0}cH0cH0}cH0}cH0}cH
Esta es en realidad la matriz para los primarios BT.709, no solo para sRGB, la segunda fila corresponde a los coeficientes luma BT.709-2 (BT.709-1 tenía un error tipográfico en estos coeficientes).
Desde CIE XYZ hasta SRGB
Los valores CIE XYZ deben escalarse para que el Y de D65 ("blanco") sea 1,0 (X = 0,9505, Y = 1,0000, Z = 1,0890). Esto suele ser cierto, pero algunos espacios de color usan 100 u otros valores (como en CIELAB, cuando se usan puntos blancos específicos).
El primer paso en el cálculo de sRGB de CIE XYZ es una transformación lineal, que puede realizarse mediante una multiplicación de matrices. (Los valores numéricos a continuación coinciden con los de la especificación oficial sRGB, que corrigió pequeños errores de redondeo en la publicación original de los creadores de sRGB, y asumen el observador colorimétrico estándar de 2° para CIE XYZ). Esta matriz depende de la profundidad de bits.
- [RlinealGlinealBlineal]=[+3.2406− − 1.5372− − 0.4986− − 0.9689+1.8758+0,0415+0,0557− − 0.2040+1.0570][XD65YD65ZD65]{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {b}b}begin{b}begin{btrix}ccH0}cH0}cH0cH0}cH00cH0cH0cH00cH0cH00}cH00cH0cH0cH00cH0cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00cH00}cH00cH00}
Estos valores de RGB lineales no el resultado final; la corrección gamma todavía debe ser aplicada. La siguiente fórmula transforma los valores lineales en sRGB:
- 0.0031308end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">CSRGB={}12.92Clineal,Clineal≤ ≤ 0,00313081.055()Clineal1/2.4)− − 0,055,Clineal■0,0031308{displaystyle C_{text{sRGB}={begin{cases}12.92C_{text{linear}}}, implicaC_{text{linear}}leq 0.0031308[5mu]1.055(C_{text{linear}}}{1/2.4})-0.055, convictC_{text{linear}08}31}0}
0.0031308end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert skin-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/812fc5729883b87d4e375b41e3eb3fe605de3e5a" style="vertical-align: -3.171ex; width:55.024ex; height:7.509ex;"/>
Donde C{displaystyle C} es R{displaystyle R., G{displaystyle G.o B{displaystyle B}.
Estos valores comprimidos gamma (a veces llamados "valores no lineales") generalmente se recortan en el rango de 0 a 1. Este recorte se puede realizar antes o después del cálculo de gamma, o como parte de la conversión a 8 bits. Si se requieren valores en el rango de 0 a 255, p.e. para visualización de vídeo o gráficos de 8 bits, la técnica habitual es multiplicar por 255 y redondear a un número entero.
Uso

Debido a la estandarización de sRGB en Internet, en computadoras e impresoras, muchas cámaras digitales y escáneres de consumo de gama baja a media utilizan sRGB como espacio de color de trabajo predeterminado (o único disponible). Sin embargo, los CCD de consumo normalmente no están calibrados, lo que significa que aunque la imagen esté etiquetada como sRGB, no se puede concluir que la imagen sea sRGB con precisión de color.
Si se desconoce el espacio de color de una imagen y es un formato de imagen de 8 bits, sRGB suele ser el valor predeterminado, en parte porque los espacios de color con una gama más grande necesitan una mayor profundidad de bits para mantener una tasa de error de color baja ( ∆E). Se puede utilizar un perfil ICC o una tabla de búsqueda para convertir sRGB a otros espacios de color. Los perfiles ICC para sRGB se distribuyen ampliamente, y ICC distribuye varias variantes de perfiles sRGB, incluidas variantes para ICCmax, versión 4 y versión 2. Generalmente se recomienda la versión 4, pero la versión 2 todavía se usa comúnmente y es la más compatible con otros software, incluidos los navegadores. La versión 2 de la especificación del perfil ICC no admite oficialmente la codificación de curvas paramétricas por partes ("para"), aunque la versión 2 sí admite funciones simples de ley de potencia. Sin embargo, las tablas de búsqueda se utilizan con mayor frecuencia porque son computacionalmente más eficientes. Incluso cuando se utilizan curvas paramétricas, el software a menudo se reduce a una tabla de búsqueda en tiempo de ejecución para un procesamiento eficiente.
Dado que la gama sRGB iguala o supera la gama de una impresora de inyección de tinta de gama baja, una imagen sRGB a menudo se considera satisfactoria para la impresión doméstica. A veces, los profesionales de la edición impresa de alto nivel evitan sRGB porque su gama de colores no es lo suficientemente grande, especialmente en los colores azul-verde, para incluir todos los colores que se pueden reproducir en la impresión CMYK. Las imágenes destinadas a la impresión profesional mediante un flujo de trabajo totalmente gestionado en color (por ejemplo, salida de preimpresión) a veces utilizan otro espacio de color como Adobe RGB (1998), que se adapta a una gama más amplia. Estas imágenes utilizadas en Internet se pueden convertir a sRGB mediante herramientas de gestión de color que normalmente se incluyen con el software que funciona en estos otros espacios de color.
Las dos interfaces de programación dominantes para gráficos 3D, OpenGL y Direct3D, han incorporado soporte para la curva gamma sRGB.
OpenGL admite texturas con componentes de color codificados con gamma sRGB (introducidos por primera vez con la extensión EXT_texture_sRGB, agregado al núcleo en OpenGL 2.1) y renderizado en framebuffers codificados con gamma sRGB (introducidos por primera vez con la extensión EXT_framebuffer_sRGB, agregado al núcleo en OpenGL 3.0). El mapeo MIP correcto y la interpolación de texturas gamma sRGB tienen soporte directo de hardware en las unidades de texturizado de la mayoría de las GPU modernas (por ejemplo, nVidia GeForce 8 realiza la conversión de texturas de 8 bits a valores lineales antes de interpolar esos valores) y no tiene ninguna penalización de rendimiento.
SYCC
Enmienda 1 al IEC 61966-2-1:1999, aprobada en 2003, incluye la definición de una representación de color Y′Cb′Cr llamado SYCC. Aunque las primarías de color RGB se basan en BT.709, las ecuaciones para la transformación de sRGB a sYCC y viceversa se basan en BT.601. sYCC utiliza 8 bits para los componentes que resultan en una gama de aproximadamente 0–1 para Y; -0.5–0.5 para C. La enmienda también contiene una codificación de 10 bits o más llamada bg-sRGB donde 0–1 es mapeado -384.510...639.510, y bg-sYCC usando el mismo número de bits para una gama de aproximadamente -0.75–1.25 para Y; -1–1 para C.
Como esta conversión puede dar como resultado valores sRGB fuera del rango 0–1, la enmienda describe cómo aplicar la corrección gamma a valores negativos, aplicando −f (−x) cuando x es negativo (y f son las funciones lineales sRGB↔ descritas anteriormente). Esto también lo utiliza scRGB.
La enmienda también recomienda una matriz XYZ a sRGB de mayor precisión utilizando siete puntos decimales, para invertir con mayor precisión la matriz sRGB a XYZ (que permanece con la precisión que se muestra arriba):
- [RlinealGlinealBlineal]=[+3.2406255− − 1.5372080− − 0.4986286− − 0.9689307+1.8757561+0,0415175+0,0557101− − 0.2040211+1.0569959][XD65YD65ZD65]{fnMicrosoft} {fnMicrosoft} {f}b}cH}cH}cH}cH}ccH30}ccH30}cH30}cH0}cH30}cH30}cH0}ccH0}.
Contenido relacionado
Tabla de métodos virtuales
ALGOL Y
Hacer bucle while
API de repositorio de contenido para Java
Datosflex
















