Sonda langmuir

Una de las dos sondas de Langmuir del Instituto Sueco de Física Espacial de Uppsala a bordo del vehículo espacial de ESA Rosetta, debido a un cometa. La sonda es la parte esférica, de 50 mm de diámetro y hecha de titanio con un revestimiento superficial de nitruro de titanio.

Una sonda Langmuir es un dispositivo que se utiliza para determinar la temperatura de los electrones, la densidad de los electrones y el potencial eléctrico de un plasma. Funciona insertando uno o más electrodos en un plasma, con un potencial eléctrico constante o variable en el tiempo entre los distintos electrodos o entre ellos y el vaso circundante. Las corrientes y potenciales medidos en este sistema permiten la determinación de las propiedades físicas del plasma.

Característica I-V de la vaina de Debye

El comienzo de la teoría de la sonda Langmuir es la característica I-V de la vaina Debye, es decir, la densidad actual fluyendo a una superficie en un plasma como una función de la caída de tensión a través de la vaina. El análisis presentado aquí indica cómo la temperatura del electrón, la densidad del electrón y el potencial del plasma pueden derivarse del I-V característica. En algunas situaciones un análisis más detallado puede producir información sobre la densidad de iones (ni{displaystyle No.), la temperatura ion Ti{displaystyle T_{i}, o la función de distribución de energía electrones (EEDF) o fe()v){displaystyle f_{e}(v)}.

Densidad de corriente de saturación de iones

Considere primero una superficie polarizada a un gran voltaje negativo. Si el voltaje es lo suficientemente grande, esencialmente todos los electrones (y los iones negativos) serán repelidos. La velocidad del ion satisfará el criterio de la cubierta de Bohm, que es, estrictamente hablando, una desigualdad, pero que generalmente se cumple marginalmente. El criterio de Bohm en su forma marginal dice que la velocidad del ion en el borde de la vaina es simplemente la velocidad del sonido dada por

cs=kB()ZTe+γ γ iTi)/mi{displaystyle C_{s}={sqrt {k_{B}(ZT_{e}+gamma - Sí..

El término de temperatura ion es a menudo descuidado, que se justifica si los iones son fríos. Incluso si se sabe que los iones son cálidos, la temperatura ion generalmente no se conoce, por lo que se supone que es simplemente igual a la temperatura del electrón. En ese caso, la consideración de la temperatura de iones finitos sólo resulta en un pequeño factor numérico. Z es el (promedio) estado de carga de los iones, y γ γ i{displaystyle gamma _{i} es el coeficiente adiabático para los iones. La elección adecuada de γ γ i{displaystyle gamma _{i} es una cuestión de cierta contención. La mayoría de los análisis usan γ γ i=1{displaystyle gamma ¿Qué?, correspondiente a iones isotérmicos, pero alguna teoría cinética sugiere que γ γ i=3{displaystyle gamma _{i}=3}. Para Z=1{displaystyle Z=1} y Ti=Te{displaystyle T_{i}=T_{e}, utilizando los resultados de mayor valor en la conclusión de que la densidad es 2{displaystyle {sqrt {2}} veces más pequeño. Las incertidumbres de esta magnitud surgen varios lugares en el análisis de datos de sonda Langmuir y son muy difíciles de resolver.

La densidad de carga de los iones depende del estado de carga Z, pero la quasineutralidad permite que uno lo escriba simplemente en términos de la densidad de electrones como qene{displaystyle q_{e}n_{e}, donde qe{displaystyle q_{e} es la carga de un electrón y ne{displaystyle n_{e} es la densidad número de electrones.

Usando estos resultados tenemos la densidad de corriente a la superficie debido a los iones. La densidad de corriente a voltajes negativos grandes se debe únicamente a los iones y, a excepción de los posibles efectos de expansión de la cubierta, no depende del voltaje de polarización, por lo que es denominada densidad de corriente de saturación de iones y viene dada por

jimax=qenecs{displaystyle ¿Qué? Donde cs{displaystyle C_{s} se define arriba.

Los parámetros del plasma, en particular, la densidad, son los del borde de la vaina.

Corriente de electrones exponencial

A medida que se reduce el voltaje de la vaina de Debye, los electrones más energéticos pueden superar la barrera de potencial de la vaina electrostática. Podemos modelar los electrones en el borde de la vaina con una distribución de Maxwell-Boltzmann, es decir,

f()vx)dvx∝ ∝ e− − 12mevx2/kBTe{displaystyle f(v_{x},dv_{x}propto e^{-{frac} {2}}m_{e}v_{x} {2}/k_{B}T_{e}},

excepto que falta la cola de alta energía que se aleja de la superficie, porque solo se reflejan los electrones de menor energía que se mueven hacia la superficie. Los electrones de mayor energía superan el potencial de la envoltura y son absorbidos. La velocidad media de los electrones que son capaces de superar el voltaje de la vaina es

.. ve.. =∫ ∫ ve0JUEGO JUEGO f()vx)vxdvx∫ ∫ − − JUEGO JUEGO JUEGO JUEGO f()vx)dvx{fnK} {f} {f}} {f}} {f} {f}}} {f}}} {f}}}},v_{x},dv_{x} {f} {f} {f}}} {f}}} {f}}}} {f}}}} {f}}}}} {f}}}}}}} {f}}}}} {f}}}}}}}} {f}}} {f}}}}} {f}}}}}}}}}}}} {f}}}}}}}}} {f}}}}}}}}} {f}}}}}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}} {,

donde la velocidad de corte para la integral superior es

ve0=2qeΔ Δ V/me{displaystyle v_{e0}={sqrt {2q_{e}Delta V/m_{e}}}.

Δ Δ V{displaystyle Delta V} es el voltaje a través de la vaina Debye, es decir, el potencial en el borde de la vaina menos el potencial de la superficie. Para un voltaje grande en comparación con la temperatura del electrón, el resultado es

.. ve.. =kBTe2π π mee− − qeΔ Δ V/kBTe{displaystyle langle v_{e}rangle ={sqrt {frac {k_{B}T_{e}{2pi} ¿Qué? Delta V/k_{B}T_{e}}.

Con esta expresión, podemos escribir la contribución de electrones a la corriente de la sonda en términos de la corriente de saturación de iones como

je=jimaxmi/2π π mee− − qeΔ Δ V/kBTe{displaystyle ¿Qué? {m_{i}/2pi} ¿Qué? Delta V/k_{B}T_{e}},

válido siempre que la corriente de electrones no sea más de dos o tres veces la corriente de iones.

Potencial flotante

La corriente total, por supuesto, es la suma de las corrientes de iones y electrones:

j=jimax()− − 1+mi/2π π mee− − qeΔ Δ V/kBTe){displaystyle j=j_{i} {max}left(-1+{sqrt {m_{i}/2pi} ¿Qué? Delta V/k..

Estamos usando la convención de que la corriente desde la superficie hacia el plasma es positiva. Una pregunta interesante y práctica es el potencial de una superficie a la que no fluye corriente neta. De la ecuación anterior se ve fácilmente que

Δ Δ V=()kBTe/qe)()1/2)In⁡ ⁡ ()mi/2π π me){displaystyle Delta V=(k_{B}T_{e}/q_{e}),(1/2)ln(m_{i}/2pi m_{e})}.

Si presentamos la masa reducida de iones μ μ i=mi/me{displaystyle mu ¿Qué?, podemos escribir

Δ Δ V=()kBTe/qe)()2.8+0.5In⁡ ⁡ μ μ i){displaystyle Delta V=(k_{B}T_{e}/q_{e}),(2.8+0.5ln mu _{i})}

Dado que el potencial flotante es la cantidad experimentalmente accesible, la corriente (por debajo de la saturación de electrones) generalmente se escribe como

j=jimax()− − 1+eqe()V0− − Δ Δ V)/kBTe){displaystyle j=j_{i}{max}left(-1+,e^{q_{e}(V_{0}- Delta V..

Corriente de saturación de electrones

Cuando el potencial de electrodo es igual o mayor que el potencial de plasma, entonces ya no hay una vaina para reflejar electrones, y la corriente de electrones satura. Usando la expresión Boltzmann para la velocidad de electrones media dada arriba con ve0=0{displaystyle v_{e0}=0} y establecer la corriente ion a cero, el densidad de corriente de saturación electrones lo haría

jemax=jimaxmi/π π me=jimax()24.2μ μ i){displaystyle ¿Qué? {m_{i}/pi ¿Qué?

Aunque esta es la expresión que suele darse en las discusiones teóricas de las sondas de Langmuir, la derivación no es rigurosa y la base experimental es débil. La teoría de las dobles capas suele emplear una expresión análoga al criterio de Bohm, pero con los roles de los electrones y los iones invertidos, a saber

jemax=qenekB()γ γ eTe+Ti)/me=jimaxmi/me=jimax()42,8μ μ i){displaystyle ### {fn} {fn} {fn} {fn} {fn}} {fn} {fn} {fnfn} {fn}}} {fnfn}}} {fnfn}}fnf}fnfnh}fnfnfnh}}}}}}}fnh}}}}}\\fn}}}}\\\fnfn}}}}\\\cH00}\cH00}}}}}}}}}}}\\\\\\cH00}}}}}\\cH\\cH00}\cHcH00}cH00}}cH00}}cH00}}cH00}}}cH00}cH00}}}}}}}}cH {k_{B}(gamma) ¿Por qué? {m_{i}/m_{e}=j_{i} {max}left(42.8,{sqrt {mu}}derecho)}

donde se encontró el valor numérico tomando T_i=T_e y γ_i=γ_e.

En la práctica, medir experimentalmente la corriente de saturación de electrones suele ser difícil y, por lo general, se considera poco informativo. Cuando se mide, se encuentra que es muy variable y generalmente mucho más bajo (un factor de tres o más) que el valor dado anteriormente. A menudo, una saturación clara no se ve en absoluto. Comprender la saturación de electrones es uno de los problemas pendientes más importantes de la teoría de la sonda de Langmuir.

Efectos del plasma a granel

La teoría de la vaina de Debye explica el comportamiento básico de las sondas de Langmuir, pero no está completa. Simplemente insertando un objeto como una sonda en un plasma cambia la densidad, la temperatura y el potencial en el borde de la vaina y quizás en todas partes. Cambiar el voltaje en la sonda también cambiará, en general, varios parámetros del plasma. Dichos efectos se comprenden menos que la física de la cubierta, pero al menos en algunos casos pueden explicarse aproximadamente.

Prevaina

El criterio de Bohm requiere que los iones entren en la vaina de Debye a la velocidad del sonido. La caída potencial que los acelera a esta velocidad se llama pre-vaina. Tiene una escala espacial que depende de la física de la fuente de iones, pero que es grande en comparación con la longitud de Debye y, a menudo, del orden de las dimensiones del plasma. La magnitud de la caída de potencial es igual a (al menos)

CCPR CCPR pre=12mics2Ze=kB()Te+Zγ γ iTi)/()2Ze){displaystyle Phi _{pre}={frac {frac {2}m_{i}c_{2} {Ze}=k_{B}(T_{e}+Zgamma) ¿Qué?

La aceleración de los iones también implica una disminución en la densidad, generalmente por un factor de aproximadamente 2 dependiendo de los detalles.

Resistividad

Las colisiones entre iones y electrones también afectarán la característica I-V de una sonda Langmuir. Cuando un electrodo está polarizado a cualquier voltaje que no sea el potencial flotante, la corriente que consume debe pasar a través del plasma, que tiene una resistividad finita. La resistividad y la trayectoria de la corriente se pueden calcular con relativa facilidad en un plasma no magnetizado. En un plasma magnetizado, el problema es mucho más difícil. En cualquier caso, el efecto es agregar una caída de voltaje proporcional a la corriente consumida, lo que corta la característica. Por lo general, no es posible observar directamente la desviación de una función exponencial, por lo que el aplanamiento de la característica generalmente se malinterpreta como una temperatura de plasma más alta. Mirándolo desde el otro lado, cualquier característica I-V medida puede interpretarse como un plasma caliente, donde la mayor parte del voltaje cae en la vaina de Debye, o como un plasma frío, donde la mayor parte del voltaje cae. se deja caer en el plasma a granel. Sin un modelo cuantitativo de la resistividad global, las sondas de Langmuir solo pueden dar un límite superior de la temperatura de los electrones.

Expansión de la vaina

No es suficiente conocer la densidad de corriente en función del voltaje de polarización ya que es la corriente absoluta la que se mide. En un plasma no magnetizado, el área de recolección de corriente generalmente se toma como el área de la superficie expuesta del electrodo. En un plasma magnetizado, se toma el área proyectada, es decir, el área del electrodo visto a lo largo del campo magnético. Si el electrodo no está a la sombra de una pared u otro objeto cercano, entonces el área debe duplicarse para tener en cuenta la corriente que viene a lo largo del campo desde ambos lados. Si las dimensiones del electrodo no son pequeñas en comparación con la longitud de Debye, entonces el tamaño del electrodo aumenta efectivamente en todas las direcciones por el espesor de la vaina. En un plasma magnetizado, a veces se supone que el electrodo aumenta de manera similar el radio de Larmor del ion.

El radio finito de Larmor permite que algunos iones lleguen al electrodo que, de lo contrario, habrían pasado. Los detalles del efecto no se han calculado de forma totalmente coherente.

Si nos referimos al área de sonda incluyendo estos efectos como Aeff{displaystyle A_{eff} (que puede ser una función del voltaje del sesgo) y hacer las suposiciones

• Ti=Te{displaystyle T_{i}=T_{e},
• Z=1{displaystyle Z=1}
• γ γ i=3{displaystyle gamma _{i}=3}, y
• ne,sh=0.5ne{displaystyle No.,

e ignorar los efectos de

• resistencia a granel, y
• saturación de electrones,

entonces la característica I-V se convierte en

I=Iimax()− − 1+eqe()Vpr− − Vfl)/()kBTe)){displaystyle I=I_{i}{max}(-1+e^{q_{e}(V_{pr}-V_{fl})/(k_{B}T_{e})}},

dónde

Iimax=qenekBTe/miAeff{displaystyle Yo... {k_{B}T_{e}/m_{i},A_{eff}.

Plasmas magnetizados

La teoría de las sondas de Langmuir es mucho más compleja cuando el plasma está magnetizado. La extensión más simple del caso no magnetizado es simplemente usar el área proyectada en lugar del área superficial del electrodo. Para un cilindro largo lejos de otras superficies, esto reduce el área efectiva por un factor de π/2 = 1,57. Como se mencionó anteriormente, podría ser necesario aumentar el radio en aproximadamente el radio de Larmor de iones térmicos, pero no por encima del área efectiva para el caso no magnetizado.

El uso del área proyectada parece estar estrechamente relacionado con la existencia de una vaina magnética. Su escala es el radio de Larmor del ion a la velocidad del sonido, que normalmente se encuentra entre las escalas de la vaina de Debye y la prevaina. El criterio de Bohm para los iones que entran en la vaina magnética se aplica al movimiento a lo largo del campo, mientras que a la entrada de la vaina de Debye se aplica al movimiento normal a la superficie. Esto da como resultado una reducción de la densidad por el seno del ángulo entre el campo y la superficie. El aumento asociado en la longitud de Debye debe tenerse en cuenta al considerar la falta de saturación de iones debido a los efectos de la vaina.

Especialmente interesante y difícil de entender es el papel de las corrientes de campo cruzado. Ingenuamente, uno esperaría que la corriente fuera paralela al campo magnético a lo largo de un tubo de flujo. En muchas geometrías, este tubo de flujo terminará en una superficie en una parte distante del dispositivo, y este punto debería exhibir una característica I-V. El resultado neto sería la medición de una característica de doble sonda; en otras palabras, corriente de saturación de electrones igual a la corriente de saturación de iones.

Cuando se considera esta imagen en detalle, se ve que el tubo de flujo debe cargarse y el plasma circundante debe girar a su alrededor. La corriente que entra o sale del tubo de flujo debe estar asociada con una fuerza que ralentiza este giro. Las fuerzas candidatas son la viscosidad, la fricción con los neutros y las fuerzas de inercia asociadas con los flujos de plasma, ya sean constantes o fluctuantes. No se sabe qué fuerza es más fuerte en la práctica y, de hecho, generalmente es difícil encontrar una fuerza que sea lo suficientemente poderosa para explicar las características realmente medidas.

También es probable que el campo magnético desempeñe un papel decisivo en la determinación del nivel de saturación de electrones, pero aún no se dispone de una teoría cuantitativa.

Configuraciones de electrodos

Una vez que se tiene una teoría de la característica I-V de un electrodo, se puede proceder a medirlo y luego ajustar los datos con la curva teórica para extraer los parámetros del plasma. La forma sencilla de hacer esto es barrer el voltaje en un solo electrodo, pero, por varias razones, en la práctica se usan configuraciones que usan múltiples electrodos o exploran solo una parte de la característica.

Sonda única

La forma más sencilla de medir la característica I-V de un plasma es con una sonda única, que consiste en un electrodo polarizado con una rampa de voltaje en relación con el recipiente. Las ventajas son la simplicidad del electrodo y la redundancia de la información, es decir, se puede comprobar si la característica I-V tiene la forma esperada. Se puede extraer información potencialmente adicional de los detalles de la característica. Las desventajas son una electrónica de medición y polarización más compleja y una resolución temporal deficiente. Si hay fluctuaciones (como siempre) y el barrido es más lento que la frecuencia de fluctuación (como suele ser), entonces I-V es la corriente promedio en función de tensión, lo que puede dar lugar a errores sistemáticos si se analiza como si fuera un I-V instantáneo. La situación ideal es barrer el voltaje a una frecuencia por encima de la frecuencia de fluctuación pero aún por debajo de la frecuencia del ciclotrón de iones. Esto, sin embargo, requiere una electrónica sofisticada y mucho cuidado.

Doble sonda

Un electrodo puede ser sesgado en relación con un segundo electrodo, en lugar de al suelo. La teoría es similar a la de una sola sonda, excepto que la corriente está limitada a la corriente de saturación de iones tanto para voltajes positivos como negativos. En particular, si Vbias{displaystyle V_{bias} es el voltaje aplicado entre dos electrodos idénticos, la corriente es dada por;

I=Iimax()− − 1+eqe()V2− − Vfl)/kBTe)=− − Iimax()− − 1+eqe()V1− − Vfl)/kBTe){displaystyle I=I_{i}{max}left(-1+,e^{q_{e}(V_{2}-V_{fl})/k_{B}T_{e}right)=-I_{max}left(-1+,e^{q_{e}(V_{1}-V_{i})/i},

que puede ser reescrito utilizando Vbias=V2− − V1{displaystyle V_{bias}=V_{2}-V_{1} como un tangente hiperbólico:

I=IimaxTanh⁡ ⁡ ()12qeVbiaskBTe){displaystyle I=I_{i}{max}tanh left({frac {1}{2},{frac} {q_{e}V_{bias} {k_{B}}right)}.

Una ventaja de la doble sonda es que ni el electrodo está muy por encima de flotar, por lo que se evitan las incertidumbres teóricas de las grandes corrientes de electrones. Si se desea probar más de la porción de electrones exponencial de la característica, una sonda doble asimétrica se puede utilizar, con un electrodo más grande que el otro. Si la proporción de las áreas de colección es mayor que la raíz cuadrada de la relación de ion a masa de electrones, entonces este arreglo es equivalente a la sonda de punta única. Si la relación de las áreas de colección no es tan grande, entonces la característica estará entre la configuración de doble punta simétrica y la configuración de una sola punta. Si A1{displaystyle A_{1} es el área de la punta más grande entonces:

I=A1Jimax[Coth⁡ ⁡ ()qeVbias2kBTe)+()A1A2− − 1)e− − qeVbias/2kBTe2pecado⁡ ⁡ ()qeVbias2kBTe)]− − 1{displaystyle I=A_{1}J_{i} {max}left[coth left({frac {q_{e}V_{bias} {2k_{B}}}right)+{frac {left({frac} {A_{1}{A_{2}}}}i} {fnfnfn} {fn} {fn} {fnfn}} {fnhfnhfnh} {fnhfnhfnh} {fnfnhfnh00} {fnfnhfnhfnh00}}}fnfnfnfnfnfnfnKfnKfnKfnKfnKfnfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnh00}}}}fnKfnKfnK}}}}fnK {fnMicrosoft Sans} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}} {fnK}}} {fnMicrosoft Sans Serif}}} {fnK}}}} {f}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}} {m}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {m}}}}}}}}}}}}}}}} {

Otra ventaja es que no hay referencia a la vasija, por lo que hasta cierto punto es inmune a las perturbaciones en un plasma de radiofrecuencia. Por otro lado, comparte las limitaciones de una sola sonda en cuanto a electrónica complicada y baja resolución de tiempo. Además, el segundo electrodo no sólo complica el sistema, sino que lo hace susceptible a perturbaciones por gradientes en el plasma.

Sonda triple

Una elegante configuración de electrodos es la sonda triple, que consta de dos electrodos polarizados con un voltaje fijo y un tercero que es flotante. El voltaje de polarización se elige para que sea varias veces la temperatura de los electrones, de modo que el electrodo negativo atraiga la corriente de saturación de iones que, al igual que el potencial flotante, se mide directamente. Una regla general común para este sesgo de voltaje es 3/e veces la temperatura esperada de los electrones. Debido a que la configuración de la punta polarizada es flotante, la sonda positiva puede extraer como máximo una corriente de electrones de igual magnitud y polaridad opuesta a la corriente de saturación de iones consumida por la sonda negativa, dada por:

− − I+=I− − =Iimax{displaystyle - ¿Qué?

y como antes, la punta flotante efectivamente no atrae corriente:

Ifl=0{displaystyle I_{fl}=0}.

Suponiendo que: 1.) La distribución de energía de los electrones en el plasma es maxwelliana, 2.) El camino libre medio de los electrones es mayor que la capa de iones alrededor de las puntas y mayor que el radio de la sonda, y 3.) los tamaños de la funda de la sonda son mucho más pequeños que la separación de la sonda, entonces, la corriente a cualquier sonda se puede considerar compuesta de dos partes: la cola de alta energía de la distribución de electrones de Maxwell y la corriente de saturación de iones:

Iprobe=− − Iee− − qeVprobe/()kTe)+Iimax{displaystyle I_{probe}=-I_{-q_{e}V_{probe}/(kT_{e}}+I_{i}{max}

donde la corriente I_e es la corriente térmica. Específicamente,

Ie=SJe=SneqekTe/2π π me{displaystyle I_{e}=SJ_{e}=Sn_{e}{e}{e}{sqrt {kT_{e}/2pi} #,

donde S es el área superficial, J_e es la densidad de corriente de electrones y n_e es la densidad electrónica.

Suponiendo que la corriente de saturación de iones y electrones es la misma para cada sonda, entonces las fórmulas para la corriente a cada una de las puntas de la sonda toman la forma

I+=− − Iee− − qeV+/()kTe)+Iimax{displaystyle Yo...

I− − =− − Iee− − qeV− − /()kTe)+Iimax{displaystyle Yo...

Ifl=− − Iee− − qeVfl/()kTe)+Iimax{displaystyle Yo....

Entonces es simple mostrar

()I+− − Ifl)/()I+− − I− − )=()1− − e− − qe()Vfl− − V+)/()kTe))/()1− − e− − qe()V− − − − V+)/()kTe)){fl})/(V_{+}-)/(I_{+}-I_{-}right)=left(1-e^{-q_{e}(V_{-fl}-V_{+})/(kT_{e})})right)/left(1-e^{-q_}{-e}

pero las relaciones de arriba especifican que I₊=-I₋ y I_fl =0 dar

1/2=()1− − e− − qe()Vfl− − V+)/()kTe))/()1− − e− − qe()V− − − − V+)/()kTe)){displaystyle 1/2=left(1-e^{-q_{e}(V_{+})/(kT_{e})}right)/left(1-e^{-q_{e}(V_{-}-V_{+})/(kT_{e})}right)}}}right)},

una ecuación trascendental en términos de voltajes aplicados y medidos y la incógnita T_e que en el límite q_eV_Sesgo = q_e(V₊-V₋) >> k T_e, se convierte en

()V+− − Vfl)=()kBTe/qe)In⁡ ⁡ 2{displaystyle (V_{+}-V_{fl})=(k_{B}T_{e}/q_{e})ln 2}.

Es decir, la diferencia de voltaje entre los electrodos positivo y flotante es proporcional a la temperatura de los electrones. (Esto fue especialmente importante en las décadas de 1960 y 1970, antes de que el procesamiento sofisticado de datos estuviera ampliamente disponible).

Un análisis más sofisticado de los datos de la sonda triple puede tener en cuenta factores como la saturación incompleta, la no saturación y las áreas desiguales.

Las sondas triples tienen la ventaja de una electrónica de polarización simple (no se requiere barrido), análisis de datos simple, excelente resolución de tiempo e insensibilidad a posibles fluctuaciones (ya sea impuestas por una fuente de rf o fluctuaciones inherentes). Al igual que las sondas dobles, son sensibles a los gradientes de los parámetros del plasma.

Arreglos especiales

A veces se han utilizado arreglos con cuatro (tetra sonda) o cinco (penta sonda), pero la ventaja sobre las sondas triples nunca ha sido del todo convincente. El espacio entre las sondas debe ser mayor que la longitud de Debye del plasma para evitar que se superponga la vaina de Debye.

Una sonda de placa de pines consiste en un pequeño electrodo directamente en frente de un electrodo grande, la idea es que el barrido de voltaje de la sonda grande puede perturbar el potencial del plasma en el borde de la vaina y por lo tanto agravar la dificultad de interpretación de la característica I-V. El potencial flotante del electrodo pequeño se puede utilizar para corregir los cambios de potencial en el borde de la vaina de la sonda grande. Los resultados experimentales de esta disposición parecen prometedores, pero la complejidad experimental y las dificultades residuales en la interpretación han impedido que esta configuración se convierta en estándar.

Se han propuesto varias geometrías para su uso como sondas de temperatura de iones, por ejemplo, dos puntas cilíndricas que giran una junto a la otra en un plasma magnetizado. Dado que los efectos de sombreado dependen del radio de Larmor del ion, los resultados pueden interpretarse en términos de la temperatura del ion. La temperatura del ion es una cantidad importante que es muy difícil de medir. Desafortunadamente, también es muy difícil analizar tales sondas de una manera completamente autoconsistente.

Las sondas emisivas utilizan un electrodo calentado eléctricamente o por la exposición al plasma. Cuando el electrodo tiene una polarización más positiva que el potencial del plasma, los electrones emitidos regresan a la superficie, por lo que la característica I-V apenas cambia. Tan pronto como el electrodo se polariza negativamente con respecto al potencial del plasma, los electrones emitidos son repelidos y contribuyen con una gran corriente negativa. El inicio de esta corriente o, más sensiblemente, el inicio de una discrepancia entre las características de un electrodo calentado y no calentado, es un indicador sensible del potencial del plasma.

Para medir las fluctuaciones en los parámetros del plasma, se utilizan matrices de electrodos, generalmente uno pero ocasionalmente bidimensionales. Una matriz típica tiene un espacio de 1 mm y un total de 16 o 32 electrodos. Un arreglo más simple para medir las fluctuaciones es un electrodo polarizado negativamente flanqueado por dos electrodos flotantes. La corriente de saturación de iones se toma como sustituto de la densidad y el potencial flotante como sustituto del potencial de plasma. Esto permite una medición aproximada del flujo de partículas turbulentas.

CCPR CCPR turb=.. n~ ~ ev~ ~ E× × B.. ∝ ∝ .. I~ ~ imax()V~ ~ fl,2− − V~ ~ fl,1).. {displaystyle Phi _{turb}=langle {cHFF} {cHFF} {cHFF} {cHFF}} {cHFF}} {cHFF}} {cH00}}} {cHFF} {cHFF}} {cHFF}} {cH}}} {cH}} {cHFF}} {cH}}}} {ccH}}}}} {c}}}}} {ccccH}}}}}}}}}} {ccccccccccH}}}}}}}}}}}}}}}}}}}}} {cccccccccccccccccccccHcHcHcHccH}}}}}}}}}}}}}}}}}}}}} {V}_{Etimes B}rangle propto langle {tilde {I}_{i}{max}({tilde {V}_{fl,2}-{tilde {V}_{fl,1}rangle }

Sonda Langmuir cilíndrica en flujo de electrones

A menudo, la sonda Langmuir es un electrodo pequeño insertado en un plasma que está conectado a un circuito externo que mide las propiedades del plasma con respecto al suelo. El suelo es típicamente un electrodo con una superficie grande y generalmente está en contacto con el mismo plasma (muy a menudo la pared metálica de la cámara). Esto permite que la sonda mida la característica I-V del plasma. La sonda mide la corriente característica i()V){displaystyle i(V)} del plasma cuando la sonda está sesgada con un potencial V{displaystyle V}.

Fig. 1. Ilustración a la sonda Langmuir I-V

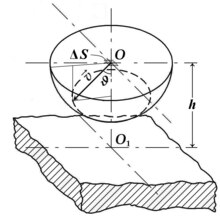
Las relaciones entre la sonda I-V característica y los parámetros del plasma isotrópico fueron encontradas por el Irving Langmuir y pueden derivarse más elementales para la sonda planar de una gran superficie Sz{displaystyle S_{z} (ignorando el problema de los efectos del borde). Vamos a elegir el punto O{displaystyle O. en plasma a la distancia h{displaystyle h} desde la superficie de sonda donde el campo eléctrico de la sonda es insignificante mientras que cada electron de plasma pasando este punto podría llegar a la superficie de sonda sin colisiones con componentes de plasma: λ λ D≪ ≪ λ λ Te{displaystyle lambda _{D}ll lambda _{Te}, λ λ D{displaystyle lambda ¿Qué? es la longitud de Debye y λ λ Te{displaystyle lambda _{Te} es el camino libre de electrones calculado para su sección total de la cruz con componentes de plasma. En las inmediaciones del punto O{displaystyle O. podemos imaginar un pequeño elemento de la superficie Δ Δ S{displaystyle Delta S} paralelo a la superficie de sonda. La corriente elemental di{displaystyle di} de electrones de plasma que pasan a través Δ Δ S{displaystyle Delta S} en una dirección de la superficie de sonda se puede escribir en la forma

di=qeΔ Δ Sdn()v,Silencio Silencio )v#⁡ ⁡ Silencio Silencio {displaystyle di=q_{e}Delta Sdn(v,vartheta)vcos vartheta },

()1)

Donde v{displaystyle v} es un escalar del vector de velocidad térmica de electrones v→ → {displaystyle {vec}},

dn()v,Silencio Silencio )=nf()v)2π π pecado⁡ ⁡ Silencio Silencio 4π π dvdSilencio Silencio {displaystyle dn(v,vartheta)=nf(v){frac {2pisin vartheta } {4pi}dvdvartheta },

()2)

2π π pecado⁡ ⁡ Silencio Silencio dSilencio Silencio {displaystyle 2pi sin vartheta dvartheta } es el elemento del ángulo sólido con su valor relativo 2π π pecado⁡ ⁡ Silencio Silencio dSilencio Silencio /4π π {displaystyle 2pi sin vartheta dvartheta /4pi }, Silencio Silencio {displaystyle vartheta } es el ángulo entre perpendicular a la superficie de sonda recordado desde el punto O{displaystyle O. y el radio-vector de la velocidad térmica de electrones v→ → {displaystyle {vec}} formando una capa esférica de espesor dv{displaystyle dv} en espacio de velocidad, y f()v){displaystyle f(v)} es la función de distribución de electrones normalizada a la unidad

∫ ∫ 0JUEGO JUEGO f()v)dv=1{displaystyle int limits _{0}{infty }f(v)dv=1}.

()3)

Teniendo en cuenta las condiciones uniformes a lo largo de la superficie de la sonda (se excluyen los límites), Δ Δ S→ → Sz{displaystyle Delta Srightarrow S_{z}, podemos tomar doble integral con respecto al ángulo Silencio Silencio {displaystyle vartheta }, y con respecto a la velocidad v{displaystyle v}, de la expresión (1Después de la sustitución Eq.2) en él, para calcular una corriente total de electrones en la sonda

i()v)=qenSz14π π ∫ ∫ 2qeV/mJUEGO JUEGO f()v)dv∫ ∫ 0Especificaciones Especificaciones v#⁡ ⁡ Silencio Silencio 2π π pecado⁡ ⁡ Silencio Silencio dSilencio Silencio {displaystyle i(v)=q_{e} {frac {1}{4pi}int limits _{sqrt {2q_{e}V/m} {infty }f(v)dvint limits _{0}^{zeta }vcos vartheta 2pisin vartheta dvartheta }.

()4)

DondeV{displaystyle V} es el potencial de sonda con respecto al potencial del plasma V=0{displaystyle V=0}, 2qeV/m{displaystyle {sqrt {2q_{e}V/m}} es el valor de velocidad de electrones más bajo en el que el electrón todavía podría alcanzar la superficie de sonda cargada al potencial V{displaystyle V}, Especificaciones Especificaciones {displaystyle zeta } es el límite superior del ángulo Silencio Silencio {displaystyle vartheta } a la cual el electron tiene velocidad inicial v{displaystyle v} todavía puede llegar a la superficie de sonda con un valor cero de su velocidad en esta superficie. Eso significa el valor Especificaciones Especificaciones {displaystyle zeta } se define por la condición

v#⁡ ⁡ Especificaciones Especificaciones =2qeV/m{displaystyle vcos zeta ={sqrt {2q_{e}V/m}}.

()5)

Conducir el valor Especificaciones Especificaciones {displaystyle zeta } de Eq. (5) y sustitución en Eq. ()4), podemos obtener la sonda I-V característica (que refleja la corriente ion) en el rango de la sonda potencial <math alttext="{displaystyle -infty − − JUEGO JUEGO .V≤ ≤ 0{displaystyle - 'infty'<img alt="-infty en la forma

i()V)=qenSz4∫ ∫ 2qeV/mJUEGO JUEGO f()v)()1− − 2qeVmv2)vdv{displaystyle i(V)={frac {q_{e}nS_{4}int limits _{sqrt [2q_{e}V/m} {infty }f(v)left(1-{frac] {2q_{e}V} {mvv}}right)vdv}.

()6)

Diferenciando Eq.6) dos veces con respecto al potencial V{displaystyle V}, se puede encontrar la expresión que describe el segundo derivado de la sonda I-V característica (obtenido primero por M. J. Druyvestein

i.. .. ()V)=qe2nSz4m1Vf()2qeV/m){displaystyle i^{primeprime}(V)={frac {q_{e} {2}nS_{4m}{4m}{frac {1} {f}fleft({sqrt {2q_{e}V/m}right)}

()7)

definir la función de distribución de electrones sobre la velocidad f()2qeV/m){displaystyle fleft({sqrt {2q_{e}V/m}right)} en la forma evidente. M. J. Druyvestein ha demostrado en particular que Eqs. ()6) y (7) son válidos para la descripción del funcionamiento de la sonda de cualquier forma geométrica convexa arbitraria. Sustituyendo la función de distribución de Maxwellian:

f()0)()v)=4π π v2vp3exp⁡ ⁡ ()− − v2/vp2){displaystyle f^{(0)}(v)={frac {4}{sqrt {cH00} {cH00} {cH00} {cH00} {cH00}} {cH00}} {fn}} {fn} {cH00}} {fn}} {f}} {f}}}} {cH00}} {fn}}}}} {f} {f}}} {f}f}}}}f}f}f}f}f}f}f}}}}}}f}f}f} {fnf}f}}}\f}f}f}sqsqfnfnfnfnsqfn\\\\sqsqsqfnfnfnfnfnsqsqcH00sqfnsqcfn ¿Qué?,

()8)

Donde vp=.. v.. π π /2{displaystyle v_{p}=langle vrangle {sqrt {pi} }/2} es la velocidad más probable, en Eq. ()6) obtenemos la expresión

i()0)()V)=qen.. v.. 4Szexp⁡ ⁡ ()− − qeV/Ep){displaystyle i^{(0)}(V)={frac {q_{e}nlangle vrangle {4}S_{z}exp left(-q_{e}V/{mathcal {E}_{p}right)}.

()9)

Fig. 2. I-V Características de Langmuir Probe en Plasma Isotropic

De donde se sigue la relación muy útil en la práctica

In⁡ ⁡ ()i()0)()V)/i()0)()0))=− − qeV/Ep{displaystyle ln left(i^{(0)}(V)/i^{(0)}(0)right)=-q_{e}V/{mathcal {E}_{p}.

()10)

permitiendo a uno derivar la energía electron Ep=kBT{displaystyle {fnMithcal}_{p}=k_{B}T} (¡para la distribución de Maxwellian sólo funciona!) por una pendiente de la sonda I-V característica en una escala semilogarítmica. Así en plasmas con distribuciones de electrones isotrópicos, la corriente de electrones ith()0){displaystyle i_{th}(0)} sobre una superficie Sz=2π π rzlz{displaystyle S_{z}=2pi ¿Qué? de la sonda cilíndrica Langmuir en el potencial plasmático V=0{displaystyle V=0} se define por la velocidad térmica de electrones promedio .. v.. {displaystyle langle vrangle } y puede ser escrito como ecuación (ver Eqs. (6), (9) at V=0{displaystyle V=0})

ith()0)=qen.. v.. 14× × 2π π rzlz{displaystyle i_{th}(0)=q_{e}nlangle vrangle {frac {1}{4}}times 2pi ¿Qué?,

()11)

Donde n{displaystyle n} es la concentración de electrones, rz{displaystyle r_{z} es el radio de sonda, y lz{displaystyle l_{z} es su longitud. Es obvio que si los electrones de plasma forman un electrón viento ()flujo) enfrente el cilíndricos eje de sonda con velocidad vd≫ ≫ .. v.. {displaystyle v_{d}gg langle vrangle }, la expresión

id=envd× × 2rzlz{displaystyle i_{d}=env_{d}times 2r_{z}l_{z}

()12)

es verdad. En plasmas producidos por fuentes de arco de descarga de gas, así como fuentes inductivamente acopladas, el viento de electrones puede desarrollar el número Mach M()0)=vd/.. v.. =()π π /2)α α ≳ ≳ 1{displaystyle M^{(0)}=v_{d}/langle vrangle =({sqrt {pi }/2)alpha gtrsim 1}. Aquí el parámetro α α {displaystyle alpha } se introduce junto con el número Mach para simplificación de expresiones matemáticas. Note que ()π π /2).. v.. =vp{displaystyle ({sqrt {pi}/2)langle vrangle =v_{p}, dondevp{displaystyle V_{p} es la velocidad más probable para la función de distribución de Maxwellian, por lo que α α =vd/vp{displaystyle alpha =v_{d}/v_{p}. Por lo tanto, el caso general en que α α ≳ ≳ 1{displaystyle alpha gtrsim 1} es de interés teórico y práctico. Correspondiendo consideraciones físicas y matemáticas presentadas en Refs. [9,10] ha demostrado que en la función de distribución Maxwelliana de los electrones en un sistema de referencia que se mueve con la velocidad vd{displaystyle V_{d} a través del eje cilíndrico sonda fijada en el potencial plasmático V=0{displaystyle V=0}, la corriente de electrones en la sonda se puede escribir en la forma

Fig.3. I-V Características de la sonda cilíndrica en el paso del viento de electrones

i()0)enSz=.. v.. 4exp⁡ ⁡ ()− − α α 2/2)I0()α α 2/2)()1+α α 2()1+I1()α α 2/2)/I0()α α 2/2))){displaystyle {frac {fnMicroc}{enS_{z}={frac} {fnMicroc}}} {fnMicroc}}}}} {fnMicroc}}}} {fnMicroc {f}}}}}}}}} {fnMicroc {f}}}}}}} {f}}}}}}} {f}}}} {f}}}}}}}}}} {f}f}}}}}}}}}}}}} { {langle vrangle }{4}exp(-alpha ^{2}/2)I_{0}(alpha ^{2}/2)left(1+alpha ^{2}left(1+I_{1}(alpha ^{2}/2)/I_{0}(alpha ^{2}/2)right)},

()13)

Donde I0{displaystyle I_{0} y I1{displaystyle I_{1} son funciones Bessel de argumentos imaginarios y Eq. (13) se reduce a Eq. (11) atα α → → 0{displaystyle alpha rightarrow 0} ser reducido a Eq. (12) at α α → → JUEGO JUEGO {displaystyle alpha rightarrow infty }. El segundo derivado de la sonda I-V característica i.. .. ()V){displaystyle i^{primeprime }(V)} con respecto al potencial de sonda V{displaystyle V} se puede presentar en este caso en el formulario (ver Fig. 3)

i.. .. ()x)=enSzvp2π π 3/2()Ep/e)21x∫ ∫ 0π π ()x− − #⁡ ⁡ φ φ )exp⁡ ⁡ ()− − α α 2()x− − #⁡ ⁡ φ φ ))dφ φ {displaystyle i^{prime prime }(x)=enS_{z}{frac {v_{p}{2pi}{3/2} {\sq}sfnMitcal {fnK}} {f}} {sqrt {x}m}intlimits _{0}{f} {f} {f} {cH00}f}fnKfnK} {cH00}f}f}f}f9}fnKcH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}}cH00},

()14)

dónde

x=1α α 2VEp/e{displaystyle x={frac}{alpha ^{2}{frac {f}{m}{m} {m} {fn}} {f}}} {fn}}} {f}} {f} {f}}} {f}}} {f}}}}} {f}}}}}}}} {f}}}}}} {f}}} {f}}}f}}}}}}}}}}}}}}}} {f} {f} {f} {f}}}}}f}}}}}}}}}}}}}}}}} {f} {f} {f}f}}} {f} {f} {f}}f}f}}}}f}f}}f}f}}}}}}}}}}}}}}}}f}}}}}}}}} {E}_{p}/e}}

()15)

y la energía electron Ep/e{fnMicrosoft Sans Serif} se expresa en eV.

Todos los parámetros de la población de electrones: n{displaystyle n}, α α {displaystyle alpha }, .. v.. {displaystyle langle vrangle } y vp{displaystyle V_{p} en plasma se puede derivar de la sonda experimental I-V característica segundo derivado i.. .. ()V){displaystyle i^{primeprime }(V)} por su mejor ajuste cuadrado con la curva teórica expresada por Eq. ()14). Para el detalle y para el problema del caso general de las funciones de distribución de electrones no-Maxwellian ver.^,

Consideraciones prácticas

Para los plasmas técnicos y de laboratorio, los electrodos suelen ser alambres de tungsteno o tantalio de varias milésimas de pulgada de grosor, porque tienen un punto de fusión alto pero pueden hacerse lo suficientemente pequeños como para no perturbar el plasma. Aunque el punto de fusión es algo más bajo, a veces se usa molibdeno porque es más fácil de mecanizar y soldar que el tungsteno. Para los plasmas de fusión, se suelen utilizar electrodos de grafito con dimensiones de 1 a 10 mm porque pueden soportar las cargas de potencia más altas (también se subliman a altas temperaturas en lugar de fundirse) y dan como resultado una radiación de bremsstrahlung reducida (con respecto a los metales) debido a la bajo número atómico de carbono. Debe definirse la superficie del electrodo expuesta al plasma, p. aislando todo menos la punta de un electrodo de alambre. Si puede haber una deposición significativa de materiales conductores (metales o grafito), entonces el aislante debe estar separado del electrodo por un meander para evitar cortocircuitos.

En un plasma magnetizado, parece ser mejor elegir un tamaño de sonda varias veces mayor que el radio de iones de Larmor. Un punto de discusión es si es mejor usar sondas orgullosas, donde el ángulo entre el campo magnético y la superficie es de al menos 15°, o sondas empotradas, los cuales están incrustados en los componentes que enfrentan el plasma y generalmente tienen un ángulo de 1 a 5 °. Muchos físicos de plasma se sienten más cómodos con las sondas orgullosas, que tienen una tradición más larga y posiblemente estén menos perturbadas por los efectos de saturación de electrones, aunque esto es discutido. Las sondas empotradas, por otro lado, al ser parte de la pared, son menos perturbadoras. El conocimiento del ángulo de campo es necesario con sondas orgullosas para determinar los flujos a la pared, mientras que es necesario con sondas empotradas para determinar la densidad.

En plasmas muy calientes y densos, como los que se encuentran en la investigación de fusión, a menudo es necesario limitar la carga térmica de la sonda limitando el tiempo de exposición. Una sonda recíproca está montada en un brazo que se mueve dentro y fuera del plasma, generalmente en aproximadamente un segundo por medio de un accionamiento neumático o electromagnético que utiliza el campo magnético ambiental. Las sondas emergentes son similares, pero los electrodos descansan detrás de un escudo y solo se mueven los pocos milímetros necesarios para llevarlos al plasma cerca de la pared.

Se puede comprar una sonda Langmuir por un valor aproximado de 15 000 dólares estadounidenses, o puede ser construida por un investigador o técnico experimentado. Cuando se trabaja en frecuencias inferiores a 100 MHz, se recomienda utilizar filtros de bloqueo y tomar las precauciones de puesta a tierra necesarias.

En plasmas de baja temperatura, en los que la sonda no se calienta, la contaminación de la superficie puede convertirse en un problema. Este efecto puede causar histéresis en la curva I-V y puede limitar la corriente recolectada por la sonda. Se puede usar un mecanismo de calentamiento o un plasma de descarga luminiscente para limpiar la sonda y evitar resultados engañosos.