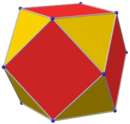
Sólida arquimediana(feminine)
En geometría, un sólido de Arquímedes es uno de los 13 sólidos enumerados por primera vez por Arquímedes. Son los poliedros uniformes convexos compuestos por polígonos regulares reunidos en vértices idénticos, excluyendo los cinco sólidos platónicos (que se componen de un solo tipo de polígono), excluyendo los prismas y antiprismas, y excluyendo el pseudorombicuboctaedro. Son un subconjunto de los sólidos de Johnson, cuyas caras poligonales regulares no necesitan encontrarse en vértices idénticos.
"Vértices idénticos" significa que cada dos vértices son simétricos entre sí: una isometría global de todo el sólido lleva un vértice al otro mientras coloca el sólido directamente en su posición inicial. Branko Grünbaum (2009) observó que un decimocuarto poliedro, la girobicúpula cuadrada alargada (o pseudo-rombicuboctaedro), cumple con una definición más débil de un sólido de Arquímedes, en el que "vértices idénticos" significa simplemente que las caras que rodean cada vértice son del mismo tipo (es decir, cada vértice se ve igual desde cerca), por lo que solo se requiere una isometría local. Grünbaum señaló un error frecuente en el que los autores definen los sólidos de Arquímedes utilizando esta definición local pero omiten el poliedro 14. Si solo se enumeran 13 poliedros, la definición debe usar simetrías globales del poliedro en lugar de vecindades locales.
Los prismas y antiprismas, cuyos grupos de simetría son los diedros, generalmente no se consideran sólidos de Arquímedes, aunque sus caras sean polígonos regulares y sus grupos de simetría actúen transitivamente sobre sus vértices. Excluyendo estas dos familias infinitas, hay 13 sólidos de Arquímedes. Todos los sólidos de Arquímedes (pero no la girobicúpula cuadrada alargada) se pueden hacer mediante construcciones de Wythoff a partir de los sólidos platónicos con simetría tetraédrica, octaédrica e icosaédrica.
Origen del nombre
Los sólidos de Arquímedes toman su nombre de Arquímedes, quien los analizó en un trabajo ahora perdido. Pappus se refiere a él, afirmando que Arquímedes enumeró 13 poliedros. Durante el Renacimiento, artistas y matemáticos valoraron las formas puras con alta simetría, y alrededor de 1620 Johannes Kepler había completado el redescubrimiento de los 13 poliedros, además de definir los prismas, antiprismas y los no convexos. sólidos conocidos como poliedros de Kepler-Poinsot. (Consulte Schreiber, Fischer & Sternath 2008 para obtener más información sobre el redescubrimiento de los sólidos de Arquímedes durante el renacimiento).
Kepler también pudo haber encontrado la girobicúpula cuadrada alargada (pseudorombocuboctaedro): al menos, una vez afirmó que había 14 sólidos de Arquímedes. Sin embargo, su enumeración publicada solo incluye los 13 poliedros uniformes, y la primera declaración clara de la existencia del pseudorombicuboctaedro fue realizada en 1905 por Duncan Sommerville.
Clasificación
Hay 13 sólidos de Arquímedes (sin contar la girobicúpula cuadrada alargada; 15 si las imágenes especulares de dos enantiomorfos, el cubo chato y el dodecaedro chato, se cuentan por separado).
Aquí la configuración de vértice se refiere al tipo de polígonos regulares que se encuentran en cualquier vértice dado. Por ejemplo, una configuración de vértice de 4.6.8 significa que un cuadrado, un hexágono y un octágono se encuentran en un vértice (tomando el orden en el sentido de las agujas del reloj alrededor del vértice).
| Nombre/ (nombre alternativo) | Schläfli Coxeter | Transparent | Sólido | Cifras netas | Vertex conf./fig. | Caras | Edges | Vert. | Volumen (puntos unidos) | Pointgroup | Sphericity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Truncated tetrahedron | t{3,3}   |   |  |  | 3.6.6 | 8 | 4 triángulos 4 hexágonos | 18 | 12 | 2.710576 | Td | 0,7574132 |
| Cuboctahedron (rhombitetratetrahedron, gyrobicupola triangular) | r{4,3} o rr{3,3} o |   |  |  | 3.4.3.4 | 14 | 8 triángulos 6 plazas | 24 | 12 | 2.357023 | Oh | 0.9049972 |
| Cubo truncado | t{4,3} |   |  |  | 3.8.8 | 14 | 8 triángulos 6 octágonos | 36 | 24 | 13.599663 | Oh | 0.8494937 |
| Truncado octaedro (Tetratetraedro truncado) | t{3,4} o tr{3,3} o |   |  |  | 4.6.6 | 14 | 6 plazas 8 hexágonos | 36 | 24 | 11.313709 | Oh | 0.9099178 |
| Rhombicuboctahedron (pequeño rhombicuboctaedro, ortobicupola cuadrada alargada) | rr{4,3} |   |  |  | 3.4.4.4 | 26 | 8 triángulos 18 plazas | 48 | 24 | 8.714045 | Oh | 0.9540796 |
| Cuboctaedro truncado (gran rhombicuboctaedro) | tr{4,3} |   |  |  | 4.6.8 | 26 | 12 plazas 8 hexágonos 6 octágonos | 72 | 48 | 41.798990 | Oh | 0.9431657 |
| Snub cube (snub cuboctahedron) | sr{4,3} |   |  |  | 3.3.3.3.4 | 38 | 32 triángulos 6 plazas | 60 | 24 | 7.889295 | O | 0.9651814 |
| Icosidodecahedron (girobirotunda pentagonal) | r{5,3} |   |  |  | 3.5.3.5 | 32 | 20 triángulos 12 pentágonos | 60 | 30 | 13.835526 | Ih | 0.9510243 |
| Truncado dodecaedro | t{5,3} |   |  |  | 3.10.10 | 32 | 20 triángulos 12 decagones | 90 | 60 | 85.039665 | Ih | 0.9260125 |
| Truncated icosahedron | t{3,5} |   |  |  | 5.6.6 | 32 | 12 pentágonos 20 hexágonos | 90 | 60 | 55.287731 | Ih | 0.9666219 |
| Rhombicosidodecahedron (pequeño rhombicosidodecedro) | rr{5,3} |   |  |  | 3.4.5.4 | 62 | 20 triángulos 30 plazas 12 pentágonos | 120 | 60 | 41.615324 | Ih | 0.9792370 |
| Truncated icosidodecahedron (gran rhombicosidodecahedron) | tr{5,3} |   |  |  | 4.6.10 | 62 | 30 plazas 20 hexágonos 12 decagones | 180 | 120 | 206.803399 | Ih | 0,9703127 |
| Snub dodecahedron (snub icosidodecahedron) | sr{5,3} |   |  |  | 3.3.3.3.5 | 92 | 80 triángulos 12 pentágonos | 150 | 60 | 37.616650 | I | 0.9820114 |
Algunas definiciones de poliedro semirregular incluyen una figura más, la girobicúpula cuadrada alargada o "pseudo-rombicuboctaedro".
Propiedades
El número de vértices es 720° dividido por el defecto del ángulo del vértice.
El cuboctaedro y el icosidodecaedro tienen aristas uniformes y se denominan cuasiregulares.
Los duales de los sólidos de Arquímedes se denominan sólidos catalanes. Junto con las bipirámides y los trapezoedros, estos son los sólidos uniformes de caras con vértices regulares.
Quiralidad
El cubo chato y el dodecaedro chato se conocen como quirales, ya que vienen en forma levógira (latín: levomorfo o laevomorfo) y diestra (latín: dextromorfo). Cuando algo viene en múltiples formas que son la imagen especular tridimensional de cada una, estas formas pueden llamarse enantiomorfas. (Esta nomenclatura también se usa para las formas de ciertos compuestos químicos).
Construcción de sólidos de Arquímedes
Los diferentes sólidos de Arquímedes y Platónicos se pueden relacionar entre sí usando un puñado de construcciones generales. Comenzando con un sólido platónico, el truncamiento implica cortar las esquinas. Para conservar la simetría, el corte se realiza en un plano perpendicular a la línea que une un vértice con el centro del poliedro y es igual para todos los vértices. Dependiendo de cuánto se trunque (consulte la tabla a continuación), se pueden crear diferentes sólidos platónicos y de Arquímedes (y otros). Si el truncamiento es exactamente lo suficientemente profundo como para que cada par de caras de vértices adyacentes compartan exactamente un punto, se conoce como rectificación. Una expansión, o cantelación, implica alejar cada cara del centro (en la misma distancia para preservar la simetría del sólido platónico) y tomar el casco convexo. La expansión con torsión también implica rotar las caras, dividiendo así cada rectángulo correspondiente a un borde en dos triángulos por una de las diagonales del rectángulo. La última construcción que usamos aquí es el truncamiento de esquinas y bordes. Ignorando la escala, la expansión también puede verse como la rectificación de la rectificación. Asimismo, el cantitruncamiento puede verse como el truncamiento de la rectificación.
| Simmetría | Tetraedral | Octahedral | Icosahedral | |||
|---|---|---|---|---|---|---|
| Inicio sólido Operación | Signatura {p,q}   | Tetraedro {3,3}  | Cube {4,3}  | Octahedron {3,4}  | Dodecahedron {5,3}  | Icosahedron {3,5}  |
| Truncación t) | t{p,q} | truncated tetrahedron | truncado cubo | truncado octaedro | truncado dodecahedron | icosahedron truncado |
| Rectificación r) Ambo (a) | r{p,q} | tetratetrahedron (octaedro)  | cuboctahedron | icosidodecahedron | ||
| Bitruncación (2t) Dual kis (dk) | 2t{p,q} | truncated tetrahedron | truncado octaedro | truncado cubo | icosahedron truncado | truncado dodecahedron |
| Birectification (2r) Dual (d) | 2r{p,q} | tetrahedron | octaedro | cube | icosahedron | dodecahedron |
| cantellation (rr) Ampliación e) | rr{p,q} | rhombitetratetrahedron (cuboctaedro)  | rhombicuboctahedron | rhombicosidodecahedron  | ||
| Snub rectified (sr) Snub (s) | sr{p,q} | snub tetratetrahedron (icosahedron)  | snub cuboctahedron | snub icosidodecahedron | ||
| Cantitruncación (tr) Bevel (b) | Tr{p,q} | truncated tetratetrahedron (octaedro truncado)  | truncated cuboctahedron | icosidodecedro truncado | ||
Observe la dualidad entre el cubo y el octaedro, y entre el dodecaedro y el icosaedro. Además, en parte porque el tetraedro es autodual, solo un sólido de Arquímedes que tiene como máximo simetría tetraédrica. (Todos los sólidos platónicos tienen al menos simetría tetraédrica, ya que la simetría tetraédrica es una operación de simetría de (es decir, está incluida en) las simetrías octaédrica e isoédrica, lo que se demuestra por el hecho de que un octaedro puede verse como un tetraedro rectificado, y un icosaedro puede ser usado como un tetraedro chato.)
Proyección estereográfica
| truncated tetrahedron | truncado cubo | truncado octaedro | truncado dodecahedron | icosahedron truncado | |||||
|---|---|---|---|---|---|---|---|---|---|
 triángulo centrado |  hexágono centrado |  octagonista |  triángulo centrado |  cuadrado centrado |  hexágono centrado |  Decagon-centered |  Triángulo centrado |  Pentágono centrado |  hexágono centrado |
| cuboctahedron | icosidodecahedron | rhombicuboctahedron | rhombicosidodecahedron | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 cuadrado centrado |  triángulo centrado |  vertex-centrado |  Pentágono centrado |  triángulo centrado |  cuadrado centrado |  cuadrado centrado |  triángulo centrado |  Pentágono centrado |  Triángulo centrado |  Centrado en la plaza | |||
| truncated cuboctahedron | icosidodecedro truncado | snub cube | ||||
|---|---|---|---|---|---|---|
 cuadrado centrado |  hexágono centrado |  octagonista |  decagon-centered |  hexágono centrado |  cuadrado centrado |  cuadrado centrado |
Referencias generales
- Jayatilake, Udaya (marzo de 2005). "Calculaciones en la cara y el vértice poliédra regular". Boletín matemático. 89 (514): 76–81. doi:10.1017/S0025557200176818. S2CID 125675814..
- Pugh, Anthony (1976). Polyhedra: Un enfoque visual. California: Universidad de California Press Berkeley. ISBN 0-520-03056-7. Capítulo 2
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Sección 3–9)
- Schreiber, Peter; Fischer, Gisela; Sternath, Maria Luise (2008). "Nueva luz sobre el redescubrimiento de los sólidos arquímicos durante el renacimiento". Archivo de Historia de las Ciencias Exactas. 62 (4): 457-467. Código:2008AHES...62..457S. doi:10.1007/s00407-008-0024-z. ISSN 0003-9519. S2CID 122216140..
Contenido relacionado
Teoría de la deformación infinitesimal
Dominio dedekind
Objetos iniciales y terminales