Solenoide

Una ilustración de un solenoide

Campo magnético creado por un solenoide de siete vías (vista transversal) descrito usando líneas de campo

Un solenoide () es un tipo de electroimán formado por una bobina helicoidal de alambre cuya longitud es sustancialmente mayor que su diámetro, que genera un campo magnético controlado. La bobina puede producir un campo magnético uniforme en un volumen de espacio cuando pasa una corriente eléctrica a través de ella. El concepto de solenoide fue introducido en 1820 por André-Marie Ampère, quien acuñó el término solenoide en 1823.

La bobina helicoidal de un solenoide no necesariamente tiene que girar alrededor de un eje rectilíneo; por ejemplo, el electroimán de William Sturgeon de 1824 consistía en un solenoide doblado en forma de herradura (similar a un resorte de arco).

Los solenoides proporcionan el enfoque magnético de los electrones en el vacío, especialmente en los tubos de las cámaras de televisión, como los vidicons y los orthicons de imagen. Los electrones toman caminos helicoidales dentro del campo magnético. Estos solenoides, bobinas de enfoque, rodean casi toda la longitud del tubo.

En ingeniería, el término "solenoide" se refiere no solo al electroimán sino a un aparato completo que proporciona un actuador que convierte la energía eléctrica en energía mecánica.

Física

Solenoide continuo infinito

Gráfico 1: Un solenoide infinito con tres bucles Ampèrian arbitrarios etiquetados a, b, y c. Integrando el camino c demuestra que el campo magnético dentro del solenoide debe ser radialmente uniforme.

Un solenoide infinito tiene una longitud infinita pero un diámetro finito. "Continuo" significa que el solenoide no está formado por bobinas discretas de ancho finito sino por muchas bobinas infinitamente delgadas sin espacio entre ellas; en esta abstracción, el solenoide a menudo se ve como una lámina cilíndrica de material conductor.

El campo magnético dentro de un solenoide infinitamente largo es homogéneo y su fuerza no depende de la distancia desde el eje ni del área de la sección transversal del solenoide.

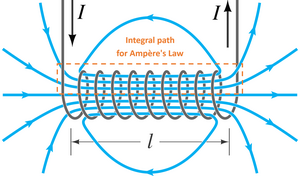
Esta es una derivación de la densidad de flujo magnético alrededor de un solenoide que es lo suficientemente larga como para ignorar los efectos marginales. En la Figura 1, sabemos de inmediato que el vector de densidad de flujo apunta en la dirección positiva z dentro del solenoide y en la dirección negativa z fuera del solenoide. Confirmamos esto aplicando la regla de agarre de la mano derecha para el campo alrededor de un cable. Si enrollamos nuestra mano derecha alrededor de un cable con el pulgar apuntando en la dirección de la corriente, la curvatura de los dedos muestra cómo se comporta el campo. Dado que estamos tratando con un solenoide largo, todas las componentes del campo magnético que no apuntan hacia arriba se cancelan por simetría. Afuera, ocurre una cancelación similar y el campo solo apunta hacia abajo.

Ahora considere el bucle imaginario c que se encuentra dentro del solenoide. Por la ley de Ampère, sabemos que la integral de línea de B (el vector de densidad de flujo magnético) alrededor de este bucle es cero, ya que no encierra corrientes eléctricas (también se puede suponer que el el campo eléctrico del circuito que pasa a través de la espira es constante en tales condiciones: una corriente constante o que cambia constantemente a través del solenoide). Hemos demostrado anteriormente que el campo apunta hacia arriba dentro del solenoide, por lo que las porciones horizontales del bucle c no contribuyen en nada a la integral. Por lo tanto, la integral del lado superior 1 es igual a la integral del lado inferior 2. Dado que podemos cambiar arbitrariamente las dimensiones del bucle y obtener el mismo resultado, la única explicación física es que los integrandos son realmente iguales, es decir, el campo magnético dentro del solenoide es radialmente uniforme. Tenga en cuenta, sin embargo, que nada prohíbe que varíe longitudinalmente, lo que de hecho ocurre.

Se puede aplicar un argumento similar al bucle a para concluir que el campo fuera del solenoide es radialmente uniforme o constante. Este último resultado, que es estrictamente cierto solo cerca del centro del solenoide donde las líneas de campo son paralelas a su longitud, es importante porque muestra que la densidad de flujo en el exterior es prácticamente cero ya que los radios del campo fuera del solenoide tenderán a infinidad. También se puede usar un argumento intuitivo para mostrar que la densidad de flujo fuera del solenoide es en realidad cero. Las líneas de campo magnético solo existen como bucles, no pueden divergir o converger en un punto como pueden hacerlo las líneas de campo eléctrico (consulte la ley de Gauss para el magnetismo). Las líneas del campo magnético siguen la trayectoria longitudinal del solenoide en el interior, por lo que deben ir en dirección opuesta al exterior del solenoide para que las líneas puedan formar bucles. Sin embargo, el volumen exterior del solenoide es mucho mayor que el volumen interior, por lo que la densidad de las líneas del campo magnético exterior se reduce considerablemente. Ahora recuerda que el campo exterior es constante. Para que se conserve el número total de líneas de campo, el campo exterior debe llegar a cero a medida que el solenoide se alarga. Por supuesto, si el solenoide se construye como un alambre en espiral (como se hace a menudo en la práctica), entonces emana un campo externo de la misma manera que un solo alambre, debido a la corriente que fluye en general a lo largo del solenoide.

La imagen muestra cómo la ley de Ampère se puede aplicar al solenoide

La aplicación de la ley del circuito de Ampère al solenoide (vea la figura de la derecha) nos da

Bl=μ μ 0NI,{displaystyle Bl=mu _{0}NI,}

Donde B{displaystyle B} es la densidad del flujo magnético, l{displaystyle l} es la longitud del solenoide, μ μ 0{displaystyle mu _{0}} es la constante magnética, N{displaystyle N} el número de vueltas, y I{displaystyle Yo... la corriente. De esto tenemos

B=μ μ 0NIl.{displaystyle B=mu - ¿Qué?.

Esta ecuación es válida para un solenoide en el espacio libre, lo que significa que la permeabilidad del camino magnético es la misma que la permeabilidad del espacio libre, μ₀.

Si el solenoide se sumerge en un material con permeabilidad relativa μ_r, entonces el campo aumenta en esa cantidad:

B=μ μ 0μ μ rNIl.{displaystyle B=mu _{0}mu ¿Qué? }{frac.

En la mayoría de los solenoides, el solenoide no está sumergido en un material de mayor permeabilidad, sino que una parte del espacio alrededor del solenoide tiene el material de mayor permeabilidad y parte es solo aire (que se comporta de manera muy similar al espacio libre). En ese escenario, no se ve el efecto completo del material de alta permeabilidad, pero habrá una permeabilidad efectiva (o aparente) μ_eff tal que 1 ≤ μ_ef ≤ μ_r.

La inclusión de un núcleo ferromagnético, como el hierro, aumenta la magnitud de la densidad de flujo magnético en el solenoide y eleva la permeabilidad efectiva de la ruta magnética. Esto se expresa mediante la fórmula

B=μ μ 0μ μ effNIl=μ μ NIl,{displaystyle B=mu _{0}mu _{mathrm {eff}{frac {be}=mu {frac {f} {f}}}}

donde μ_eff es la permeabilidad efectiva o aparente del núcleo. La permeabilidad efectiva es función de las propiedades geométricas del núcleo y su permeabilidad relativa. Los términos permeabilidad relativa (una propiedad del material) y permeabilidad efectiva (una propiedad de toda la estructura) a menudo se confunden; pueden diferir en muchos órdenes de magnitud.

Para una estructura magnética abierta, la relación entre la permeabilidad efectiva y la permeabilidad relativa es la siguiente:

μ μ eff=μ μ r1+k()μ μ r− − 1),{displaystyle mu _{mathrm {eff} }={frac {mu {}{1+k(mu _{r}-1)}}}

donde k es el factor de desmagnetización del núcleo.

Solenoide continuo finito

Línea de campo magnético y densidad creada por un solenoide con densidad de corriente superficial

Un solenoide finito es un solenoide de longitud finita. Continuo significa que el solenoide no está formado por bobinas discretas sino por una lámina de material conductor. Suponemos que la corriente se distribuye uniformemente en la superficie del solenoide, con una densidad de corriente superficial K; en coordenadas cilíndricas:

K→ → =Ilφ φ ^ ^ .{displaystyle {vec}={frac} {} {fn} {fnK}} {f}} {f}} {f}} {f}} {f}} {f}}} {f}} {f}}}} {f}}} {f}} {f}} {f}} {f}}}} {f}}}} {f}}}} {f} {f}} {f}f} {f} {f}f}f} {f}f}f}f} {f} {f} {f} {f}f}f}f}f}f}f}f} {f} {f} {f} {f} {f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f }}

El campo magnético se puede encontrar utilizando el potencial vectorial, que para un solenoide finito con radio R y longitud l en coordenadas cilíndricas ()*** *** ,φ φ ,z){displaystyle (rhophiz)} es

Aφ φ =μ μ 0Iπ π Rl[Especificaciones Especificaciones ()R+*** *** )2+Especificaciones Especificaciones 2()m+n− − mnmnK()m)− − 1mE()m)+n− − 1n▪ ▪ ()n,m))]Especificaciones Especificaciones − − Especificaciones Especificaciones +,{displaystyle A_{f}={frac {fnMicroc} ¿Qué? }{frac {R} {fn}left {fnMicroc}zeta }{2}+zeta ¿Qué? {m+n-mn} {mn}K(m)-{frac {1}{m}E(m)+{frac {n-1}{n} Pi (n,m)right)right]_{zeta ¿Qué? - ¿Qué?

Dónde:

• Especificaciones Especificaciones ± ± =z± ± l2{displaystyle zeta _{pm }=zpm {frac {I}{2}},
• n=4R*** *** ()R+*** *** )2{displaystyle n={frac {4Rrho } {cH00}}},
• m=4R*** *** ()R+*** *** )2+Especificaciones Especificaciones 2{displaystyle m={frac {4Rrho }{2}+zeta }},
• K()m)=∫ ∫ 0π π 2dSilencio Silencio 1− − mpecado2⁡ ⁡ Silencio Silencio {displaystyle K(m)=int ¿Qué? {}{2}{frac {dtheta ♫{sqrt {1-msin ^{2}theta },
• E()m)=∫ ∫ 0π π 21− − mpecado2⁡ ⁡ Silencio Silencio dSilencio Silencio {displaystyle E(m)=int ¿Qué? } {2} {sqrt {1-msin }theta },dtheta }
• ▪ ▪ ()n,m)=∫ ∫ 0π π 2dSilencio Silencio ()1− − npecado2⁡ ⁡ Silencio Silencio )1− − mpecado2⁡ ⁡ Silencio Silencio {displaystyle Pi (n,m)=int _{0}^{frac {pi {2} {fn} {fnfnsnsn}theta){sqrt {1-msin ^{2}theta }.

Aquí, K()m){displaystyle K(m)}, E()m){displaystyle E(m)}, y ▪ ▪ ()n,m){displaystyle Pi (n,m)} son integrales elípticos completos de primera, segunda y tercera clase.

Usando:

B→ → =Silencio Silencio × × A→ → ,{displaystyle {vec {bec}=nabla times {vec {}}}

La densidad de flujo magnético se obtiene como

B*** *** =μ μ 0I4π π 1l*** *** [()R+*** *** )2+Especificaciones Especificaciones 2()()m− − 2)K()m)+2E()m))]Especificaciones Especificaciones − − Especificaciones Especificaciones +,{displaystyle B_{rho ¿Qué? }{frac {1}{l,rho }left[{sqrt [R+rho]^{2}+zeta ^{2} {biggl (}(m-2)K(m)+2E(m){biggr)}right]_{zeta ¿Qué? - ¿Qué?

Bz=μ μ 0I2π π 1l[Especificaciones Especificaciones ()R+*** *** )2+Especificaciones Especificaciones 2()K()m)+R− − *** *** R+*** *** ▪ ▪ ()n,m))]Especificaciones Especificaciones − − Especificaciones Especificaciones +.{displaystyle B_{z}={frac {mu {fnK} {fnMicroc {}fnK} {fnMicroc {zeta} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}left(K(m)+{frac] {R-rho {R+rho}Pi (n,m)right]_{zeta ¿Qué? - Sí.

En el eje de simetría, la componente radial desaparece y la componente de campo axial es

Bz=μ μ 0NI2()l/2− − zlR2+()l/2− − z)2+l/2+zlR2+()l/2+z)2).{displaystyle B_{z}={frac # ¿Por qué? [R^{2}+(l/2-z)}}}}+{frac {l/2+z}{l{sqrt {R^{2}+(l/2+z)}}}right).}

l/2− − SilenciozSilencio≫ ≫ R{displaystyle l/2-responsable R.

B=μ μ 0NI/l{displaystyle B=mu - No.

Estimación de solenoide corto

Para el caso en que el radio es mucho mayor que la longitud del solenoide (R≫ ≫ l{displaystyle Rgg l}), la densidad del flujo magnético a través del centro del solenoide (en el z dirección, paralela a la longitud del solenoide, donde la bobina se centra en z=0) se puede estimar como la densidad del flujo de un solo bucle circular del conductor:

Bz.. μ μ 0INR22R2+z23{displaystyle B_{z}approx {fnMicroc {fnMicroc} ¿Qué? {cH00}}}} {}}}}}}}

Solenoides irregulares

Ejemplos de solenoides irregulares (a) solenoide escaso, b) solenoide de campo variado, c) solenoide no cilíndrico

Dentro de la categoría de solenoides finitos, hay aquellos que están escasamente enrollados con un solo paso, escasamente enrollados con varios pasos (solenoide de paso variable) o aquellos con un radio variable para diferentes bucles (solenoide no cilíndrico). Se llaman solenoides irregulares. Han encontrado aplicaciones en diferentes áreas, como solenoides escasamente enrollados para transferencia de energía inalámbrica, solenoides de paso variable para resonancia magnética nuclear (RMN) y solenoides no cilíndricos para otros dispositivos médicos.

El cálculo de la inductancia y la capacitancia intrínsecas no se puede realizar utilizando los de los solenoides tradicionales, es decir, los de bobinado hermético. Se propusieron nuevos métodos de cálculo para el cálculo de la inductancia intrínseca (códigos disponibles en) y la capacitancia. (códigos disponibles en)

Inductancia

Como se muestra anteriormente, la densidad del flujo magnético B{displaystyle B} dentro de la bobina es prácticamente constante y dado por

B=μ μ 0NIl,{displaystyle B=mu _{0}{frac} {f}}

Donde μ₀ es la constante magnética, N{displaystyle N} el número de vueltas, I{displaystyle Yo... la corriente y l{displaystyle l} la longitud de la bobina. Ignorar los efectos finales, el flujo magnético total a través de la bobina se obtiene multiplicando la densidad del flujo B{displaystyle B} por el área de la sección transversal A{displaystyle A}:

CCPR CCPR =μ μ 0NIAl.{displaystyle {fnK}}

Combinando esto con la definición de inductancia

L=NCCPR CCPR I,{displaystyle L={frac {NPhi}{I}}} {f}}}

La inductancia de un solenoide sigue como

L=μ μ 0N2Al.{displaystyle L=mu _{0}{frac {N^{2}A}}

Dellinger, Whittmore y Ould calcularon una tabla de inductancia para solenoides cortos de varias relaciones entre diámetro y longitud.

Esto, y la inductancia de formas más complicadas, se pueden derivar de las ecuaciones de Maxwell. Para bobinas rígidas con núcleo de aire, la inductancia es una función de la geometría de la bobina y el número de vueltas, y es independiente de la corriente.

Un análisis similar se aplica a un solenoide con un núcleo magnético, pero solo si la longitud de la bobina es mucho mayor que el producto de la permeabilidad relativa del núcleo magnético y el diámetro. Eso limita el análisis simple a núcleos de baja permeabilidad o solenoides extremadamente largos y delgados. La presencia de un núcleo se puede tener en cuenta en las ecuaciones anteriores reemplazando la constante magnética μ₀ con μ o μ₀μ_r, donde μ representa permeabilidad y μ_r relativo permeabilidad. Tenga en cuenta que dado que la permeabilidad de los materiales ferromagnéticos cambia con el flujo magnético aplicado, la inductancia de una bobina con un núcleo ferromagnético generalmente variará con la corriente.