Sobreajuste

Gráfico 1. La línea verde representa un modelo overfitted y la línea negra representa un modelo regularizado. Si bien la línea verde mejor sigue los datos de entrenamiento, es demasiado dependiente de esos datos y es probable que tenga una tasa de error más alta en los nuevos datos no vistos, en comparación con la línea negra.

Gráfico 2. Los datos ruidosos (aproximadamente lineales) se ajustan a una función lineal y a una función polinómica. Aunque la función polinomio es un ajuste perfecto, se puede esperar que la función lineal se generalice mejor: si las dos funciones se utilizaron para extrapolar más allá de los datos ajustados, la función lineal debe hacer mejores predicciones.

Gráfico 3. La línea azul dashed representa un modelo inadaptado. Una línea recta nunca puede encajar en una parabola. Este modelo es muy sencillo.

En modelado matemático, sobreajuste es "la producción de un análisis que se corresponde demasiado cerca o exactamente con un conjunto particular de datos, y, por lo tanto, puede no ajustarse a datos adicionales o predecir observaciones futuras de manera confiable. Un modelo sobreajustado es un modelo matemático que contiene más parámetros de los que los datos pueden justificar. La esencia del sobreajuste es haber extraído, sin saberlo, parte de la variación residual (es decir, el ruido) como si esa variación representara la estructura subyacente del modelo.

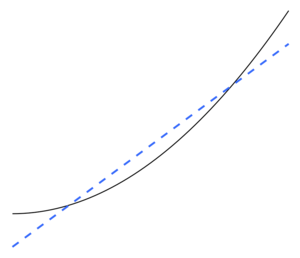
El ajuste insuficiente ocurre cuando un modelo matemático no puede capturar adecuadamente la estructura subyacente de los datos. Un modelo infraajustado es un modelo en el que faltan algunos parámetros o términos que aparecerían en un modelo especificado correctamente. Se produciría un ajuste insuficiente, por ejemplo, al ajustar un modelo lineal a datos no lineales. Dicho modelo tenderá a tener un rendimiento predictivo deficiente.

Existe la posibilidad de sobreajuste porque el criterio utilizado para seleccionar el modelo no es el mismo que el criterio utilizado para juzgar la idoneidad de un modelo. Por ejemplo, se puede seleccionar un modelo maximizando su rendimiento en algún conjunto de datos de entrenamiento y, sin embargo, su idoneidad puede estar determinada por su capacidad para funcionar bien en datos no vistos; luego se produce un ajuste excesivo cuando un modelo comienza a "memorizar" datos de entrenamiento en lugar de "aprendizaje" generalizar a partir de una tendencia.

Como ejemplo extremo, si la cantidad de parámetros es igual o mayor que la cantidad de observaciones, entonces un modelo puede predecir perfectamente los datos de entrenamiento simplemente memorizando los datos en su totalidad. (Para ver una ilustración, consulte la Figura 2). Sin embargo, dicho modelo generalmente fallará gravemente al hacer predicciones.

El potencial de sobreajuste no solo depende de la cantidad de parámetros y datos, sino también de la conformidad de la estructura del modelo con la forma de los datos y la magnitud del error del modelo en comparación con el nivel esperado de ruido o error en los datos. Incluso cuando el modelo ajustado no tiene un número excesivo de parámetros, es de esperar que la relación ajustada parezca funcionar menos bien en un nuevo conjunto de datos que en el conjunto de datos utilizado para el ajuste (un fenómeno que a veces se conoce como contracción). En particular, el valor del coeficiente de determinación se reducirá en relación con los datos originales.

Para disminuir la posibilidad o la cantidad de sobreajuste, hay varias técnicas disponibles (por ejemplo, comparación de modelos, validación cruzada, regularización, interrupción anticipada, poda, antecedentes bayesianos o abandono). La base de algunas técnicas es (1) penalizar explícitamente los modelos demasiado complejos o (2) probar la capacidad de generalización del modelo mediante la evaluación de su rendimiento en un conjunto de datos que no se utilizan para el entrenamiento, que se supone que se aproximan. los típicos datos ocultos que encontrará un modelo.

Inferencia estadística

En estadística, se extrae una inferencia de un modelo estadístico, que se ha seleccionado mediante algún procedimiento. Burnham &amperio; Anderson, en su texto muy citado sobre la selección de modelos, argumenta que para evitar el sobreajuste, debemos adherirnos al "Principio de parsimonia". Los autores también afirman lo siguiente.

Los modelos inadecuados... a menudo están libres de prejuicios en los estimadores del parámetro, pero han estimado (y real) diferencias de muestreo que son innecesariamente grandes (la precisión de los estimadores es pobre, en relación con lo que podría haberse logrado con un modelo más parsimonioso). Los efectos falsos del tratamiento tienden a ser identificados, y las variables falsas se incluyen con modelos overfitted.... Un mejor modelo de aproximación se logra equilibrando adecuadamente los errores de inadaptarse y sobreajustar.

Es más probable que el sobreajuste sea una preocupación seria cuando hay poca teoría disponible para guiar el análisis, en parte porque entonces tiende a haber una gran cantidad de modelos para seleccionar. El libro Model Selection and Model Averaging (2008) lo expresa de esta manera.

Dado un conjunto de datos, puede ajustarse a miles de modelos al pulsar un botón, pero ¿cómo elegir lo mejor? Con tantos modelos candidatos, la superación es un peligro real. ¿Es el mono el que escribió Hamlet en realidad un buen escritor?

Regresión

En el análisis de regresión, el sobreajuste ocurre con frecuencia. Como ejemplo extremo, si hay variables p en una regresión lineal con puntos de datos p, la línea ajustada puede pasar exactamente por todos los puntos. Para los modelos de regresión logística o de riesgos proporcionales de Cox, hay una variedad de reglas generales (p. ej., 5–9, 10 y 10–15; la pauta de 10 observaciones por variable independiente se conoce como la "regla de uno en diez" 34;). En el proceso de selección del modelo de regresión, el error cuadrático medio de la función de regresión aleatoria se puede dividir en ruido aleatorio, sesgo de aproximación y varianza en la estimación de la función de regresión. La compensación de sesgo-varianza se usa a menudo para superar los modelos de sobreajuste.

Con un gran conjunto de variables explicativas que en realidad no tienen relación con la variable dependiente que se predice, en general se encontrará falsamente que algunas variables son estadísticamente significativas y, por lo tanto, el investigador puede retenerlas en el modelo y, por lo tanto, sobreajustar el modelo. Esto se conoce como la paradoja de Freedman.

Aprendizaje automático

Gráfico 4. Superficie/superentrenamiento en el aprendizaje supervisado (por ejemplo, red neuronal). El error de entrenamiento se muestra en azul, error de validación en rojo, tanto como función del número de ciclos de entrenamiento. Si el error de validación aumenta (la pendiente positiva) mientras que el error de entrenamiento disminuye constantemente (la pendiente negativa) entonces puede haber ocurrido una situación de exceso. El mejor modelo predictivo y equipado sería donde el error de validación tiene su mínimo global.

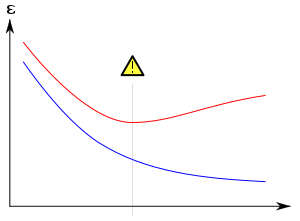
Por lo general, un algoritmo de aprendizaje se entrena utilizando algún conjunto de "datos de entrenamiento": situaciones ejemplares para las que se conoce el resultado deseado. El objetivo es que el algoritmo también funcione bien en la predicción de la salida cuando se le proporcionen "datos de validación" que no se encontró durante su entrenamiento.

El sobreajuste es el uso de modelos o procedimientos que violan la navaja de Occam, por ejemplo, al incluir más parámetros ajustables que los óptimos en última instancia, o al usar un enfoque más complicado que el óptimo en última instancia. Para un ejemplo donde hay demasiados parámetros ajustables, considere un conjunto de datos donde los datos de entrenamiento para y pueden predecirse adecuadamente mediante una función lineal de dos variables independientes. Tal función requiere solo tres parámetros (la intersección y dos pendientes). Reemplazar esta función simple con una función cuadrática nueva y más compleja, o con una función lineal nueva y más compleja en más de dos variables independientes, conlleva un riesgo: la navaja de Occam implica que cualquier función compleja dada es a a priori menos probable que cualquier función simple dada. Si se selecciona la nueva función más complicada en lugar de la función simple, y si no hubo una ganancia lo suficientemente grande en el ajuste de los datos de entrenamiento para compensar el aumento de la complejidad, entonces la nueva función compleja "sobreajusta" los datos, y la función sobreajustada compleja probablemente funcionará peor que la función más simple en los datos de validación fuera del conjunto de datos de entrenamiento, aunque la función compleja funcionó tan bien, o incluso mejor, en el conjunto de datos de entrenamiento.

Al comparar diferentes tipos de modelos, la complejidad no se puede medir únicamente contando cuántos parámetros existen en cada modelo; también se debe considerar la expresividad de cada parámetro. Por ejemplo, no es trivial comparar directamente la complejidad de una red neuronal (que puede rastrear relaciones curvilíneas) con parámetros m con un modelo de regresión con parámetros n.

El sobreajuste es especialmente probable en los casos en los que el aprendizaje se llevó a cabo durante demasiado tiempo o cuando los ejemplos de entrenamiento son raros, lo que hace que el alumno se ajuste a características aleatorias muy específicas de los datos de entrenamiento que no tienen una relación causal con la función de destino. En este proceso de sobreajuste, el rendimiento de los ejemplos de entrenamiento sigue aumentando, mientras que el rendimiento de los datos ocultos empeora.

Como ejemplo simple, considere una base de datos de compras minoristas que incluya el artículo comprado, el comprador y la fecha y hora de la compra. Es fácil construir un modelo que se ajuste perfectamente al conjunto de entrenamiento mediante el uso de la fecha y la hora de compra para predecir los otros atributos, pero este modelo no se generalizará en absoluto a nuevos datos, porque esos tiempos pasados nunca ocurrirán. de nuevo.

Por lo general, se dice que un algoritmo de aprendizaje se sobreajusta en relación con uno más simple si es más preciso para ajustar datos conocidos (retrospectiva) pero menos preciso para predecir nuevos datos (previsión). Uno puede entender intuitivamente el sobreajuste por el hecho de que la información de toda la experiencia pasada se puede dividir en dos grupos: información que es relevante para el futuro e información irrelevante ('ruido'). En igualdad de condiciones, cuanto más difícil es predecir un criterio (es decir, cuanto mayor es su incertidumbre), más ruido existe en la información pasada que debe ignorarse. El problema es determinar qué parte ignorar. Un algoritmo de aprendizaje que puede reducir el riesgo de ruido de ajuste se llama "robusto".

Consecuencias

Una fotografía de Anne Graham Lotz incluida en el conjunto de entrenamiento de la Difusión Estable, un modelo de texto a imagen

Una imagen generada por Stable Diffusion usando el impulso "Anne Graham Lotz"

Los modelos generativos inadaptados pueden producir productos prácticamente idénticos a los casos de su conjunto de formación.

La consecuencia más obvia del sobreajuste es un rendimiento deficiente en el conjunto de datos de validación. Otras consecuencias negativas incluyen:

• Una función que se supera es probable que solicite más información sobre cada artículo en el conjunto de datos de validación que la función óptima; reunir estos datos no necesarios adicionales puede ser costoso o propensa a errores, especialmente si cada pieza individual de información debe ser recopilada por observación humana y entrada manual de datos.
• Una función más compleja y superada es probable que sea menos portátil que una simple. En un extremo, una regresión lineal única es tan portátil que, si es necesario, podría incluso hacerse a mano. En el otro extremo son modelos que se pueden reproducir sólo duplicando exactamente toda la configuración del modelador original, haciendo difícil la reutilización o reproducción científica.
• Puede ser posible reconstruir los detalles de las instancias de entrenamiento individuales del conjunto de entrenamiento de un modelo de aprendizaje automático inadaptado. Esto puede ser indeseable si, por ejemplo, los datos de capacitación incluyen información confidencial de identificación personal (PII). Este fenómeno también presenta problemas en la esfera de la inteligencia artificial y los derechos de autor, con los desarrolladores de algunos modelos de aprendizaje profundo generativo como Stable Diffusion y GitHub Copilot siendo demandados por violación de derechos de autor porque estos modelos han sido encontrados para ser capaces de reproducir ciertos artículos de copyright de sus datos de formación.

Remedio

La función óptima generalmente necesita verificación en conjuntos de datos más grandes o completamente nuevos. Sin embargo, existen métodos como el árbol de expansión mínimo o el tiempo de vida de la correlación que aplica la dependencia entre los coeficientes de correlación y las series temporales (ancho de la ventana). Siempre que el ancho de la ventana sea lo suficientemente grande, los coeficientes de correlación son estables y ya no dependen del tamaño del ancho de la ventana. Por lo tanto, se puede crear una matriz de correlación calculando un coeficiente de correlación entre las variables investigadas. Esta matriz se puede representar topológicamente como una red compleja donde se visualizan las influencias directas e indirectas entre las variables. La regularización de la deserción también puede mejorar la solidez y, por lo tanto, reducir el ajuste excesivo al eliminar probabilísticamente las entradas de una capa.

Revestimiento

Figura 5. La línea roja representa un modelo inadaptado de los puntos de datos representados en azul. Esperamos ver una línea en forma de parabola para representar la curvatura de los puntos de datos.

Figura 6. La línea azul representa un modelo ajustado de los puntos de datos representados en verde.

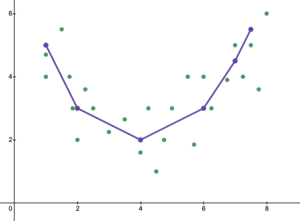
El ajuste insuficiente es lo contrario del ajuste excesivo, lo que significa que el modelo estadístico o el algoritmo de aprendizaje automático es demasiado simple para capturar con precisión los patrones en los datos. Una señal de ajuste insuficiente es que se detecta un sesgo alto y una varianza baja en el modelo o algoritmo actual utilizado (lo contrario del ajuste excesivo: sesgo bajo y varianza alta). Esto se puede deducir de la compensación Sesgo-varianza, que es el método para analizar un modelo o algoritmo en busca de error de sesgo, error de varianza y error irreducible. Con un sesgo alto y una varianza baja, el resultado del modelo es que representará de manera inexacta los puntos de datos y, por lo tanto, no podrá predecir de manera suficiente los resultados de datos futuros (consulte Error de generalización). Como se muestra en la Figura 5, la línea lineal no podría representar todos los puntos de datos dados debido a que la línea no se parece a la curvatura de los puntos. Esperaríamos ver una línea en forma de parábola como se muestra en la Figura 6 y la Figura 1. Como se mencionó anteriormente, si usáramos la Figura 5 para el análisis, obtendríamos resultados predictivos falsos contrarios a los resultados si analizáramos la Figura 6.

Burnham &amperio; Anderson afirma lo siguiente.

... un modelo inadaptado ignoraría una estructura replicable importante (es decir, conceptualmente reproducible en la mayoría de las otras muestras) en los datos y por lo tanto no identificar efectos que fueron realmente apoyados por los datos. En este caso, el sesgo en los estimadores del parámetro es a menudo sustancial, y se subestima la varianza de muestreo, ambos factores que provocan una mala cobertura del intervalo de confianza. Los modelos adaptados tienden a perder importantes efectos de tratamiento en entornos experimentales.

Resolviendo el desajuste

Hay varias formas de lidiar con la inadecuación:

1. Aumentar la complejidad del modelo: Si el modelo es demasiado simple, puede ser necesario aumentar su complejidad añadiendo más características, aumentando el número de parámetros o utilizando un modelo más flexible. Sin embargo, esto debe hacerse cuidadosamente para evitar el exceso de adaptación.
2. Use un algoritmo diferente: Si el algoritmo actual no es capaz de capturar los patrones en los datos, puede ser necesario probar uno diferente. Por ejemplo, una red neuronal puede ser más eficaz que un modelo de regresión lineal para algunos tipos de datos.
3. Aumentar la cantidad de datos de capacitación: Si el modelo se está adaptando debido a la falta de datos, aumentar la cantidad de datos de capacitación puede ayudar. Esto permitirá al modelo capturar mejor los patrones subyacentes en los datos.
4. Regularización: La regularización es una técnica utilizada para prevenir el exceso de ajuste añadiendo un plazo de penalización a la función de pérdida que desalienta los grandes valores del parámetro. También se puede utilizar para prevenir la inadaptación controlando la complejidad del modelo.
5. Ensemble Methods: Los métodos Ensemble combinan múltiples modelos para crear una predicción más precisa. Esto puede ayudar a reducir la insuficiencia permitiendo que múltiples modelos trabajen juntos para capturar los patrones subyacentes en los datos.
6. Ingeniería de características: La ingeniería de características implica la creación de nuevas características modelo de las existentes que pueden ser más relevantes para el problema a la mano. Esto puede ayudar a mejorar la precisión del modelo y prevenir la adaptación.