Sistema dinámico
En matemáticas, un sistema dinámico es un sistema en el que una función describe la dependencia temporal de un punto en un espacio ambiental. Los ejemplos incluyen los modelos matemáticos que describen el movimiento del péndulo de un reloj, el flujo de agua en una tubería, el movimiento aleatorio de las partículas en el aire y la cantidad de peces en un lago cada primavera. La definición más general unifica varios conceptos matemáticos, como las ecuaciones diferenciales ordinarias y la teoría ergódica, al permitir diferentes opciones de espacio y forma de medir el tiempo. El tiempo puede medirse por números enteros, por números reales o complejos o puede ser un objeto algebraico más general, perdiendo la memoria de su origen físico, y el espacio puede ser una variedad o simplemente un conjunto, sin necesidad de un espacio-tiempo uniforme. estructura definida en él.
En un momento dado, un sistema dinámico tiene un estado que representa un punto en un espacio de estado apropiado. Este estado suele estar dado por una tupla de números reales o por un vector en una variedad geométrica. La regla de evolución del sistema dinámico es una función que describe qué estados futuros se derivan del estado actual. A menudo, la función es determinista, es decir, para un intervalo de tiempo dado, solo se sigue un estado futuro del estado actual. Sin embargo, algunos sistemas son estocásticos, en el sentido de que los eventos aleatorios también afectan la evolución de las variables de estado.
En física, un sistema dinámico se describe como una "partícula o conjunto de partículas cuyo estado varía con el tiempo y, por lo tanto, obedece a ecuaciones diferenciales que implican derivadas temporales". Con el fin de realizar una predicción sobre el comportamiento futuro del sistema, se realiza una solución analítica de dichas ecuaciones o su integración en el tiempo mediante simulación por computadora.
El estudio de los sistemas dinámicos es el foco de la teoría de los sistemas dinámicos, que tiene aplicaciones en una amplia variedad de campos como las matemáticas, la física, la biología, la química, la ingeniería, la economía, la historia y la medicina. Los sistemas dinámicos son una parte fundamental de la teoría del caos, la dinámica de mapas logísticos, la teoría de la bifurcación, los procesos de autoensamblaje y autoorganización, y el concepto de borde del caos.
Resumen
El concepto de sistema dinámico tiene su origen en la mecánica newtoniana. Allí, como en otras disciplinas de las ciencias naturales y la ingeniería, la regla de evolución de los sistemas dinámicos es una relación implícita que da el estado del sistema solo por un breve período de tiempo en el futuro. (La relación es una ecuación diferencial, una ecuación en diferencias u otra escala de tiempo). Para determinar el estado de todos los tiempos futuros, es necesario iterar la relación muchas veces, cada vez que avanza un pequeño paso. El procedimiento de iteración se conoce como resolver el sistema o integrar el sistema. Si el sistema se puede resolver, dado un punto inicial es posible determinar todas sus posiciones futuras, un conjunto de puntos conocido como trayectoria u órbita.
Antes de la llegada de las computadoras, encontrar una órbita requería técnicas matemáticas sofisticadas y solo podía lograrse para una pequeña clase de sistemas dinámicos. Los métodos numéricos implementados en máquinas de computación electrónica han simplificado la tarea de determinar las órbitas de un sistema dinámico.
Para sistemas dinámicos simples, conocer la trayectoria suele ser suficiente, pero la mayoría de los sistemas dinámicos son demasiado complicados para comprenderlos en términos de trayectorias individuales. Las dificultades surgen porque:
- Los sistemas estudiados sólo pueden ser conocidos aproximadamente—los parámetros del sistema pueden no ser conocidos precisamente o los términos pueden faltar de las ecuaciones. Las aproximaciones utilizadas ponen en tela de juicio la validez o relevancia de las soluciones numéricas. Para abordar estas cuestiones se han introducido varias nociones de estabilidad en el estudio de sistemas dinámicos, como la estabilidad de Lyapunov o la estabilidad estructural. La estabilidad del sistema dinámico implica que hay una clase de modelos o condiciones iniciales para las cuales las trayectorias serían equivalentes. La operación para comparar órbitas para establecer sus cambios de equivalencia con las diferentes nociones de estabilidad.
- El tipo de trayectoria puede ser más importante que una trayectoria particular. Algunas trayectorias pueden ser periódicas, mientras que otras pueden pasar por muchos estados diferentes del sistema. Las aplicaciones a menudo requieren enumerar estas clases o mantener el sistema dentro de una clase. Clasificación de todas las trayectorias posibles ha llevado al estudio cualitativo de sistemas dinámicos, es decir, propiedades que no cambian bajo cambios coordinados. Los sistemas y sistemas dinámicos lineales que tienen dos números que describen un estado son ejemplos de sistemas dinámicos donde se entienden las posibles clases de órbitas.
- El comportamiento de las trayectorias como función de un parámetro puede ser lo que se necesita para una aplicación. Como un parámetro es variado, los sistemas dinámicos pueden tener puntos de bifurcación donde el comportamiento cualitativo del sistema dinámico cambia. Por ejemplo, puede pasar de tener sólo movimientos periódicos a comportamiento aparentemente errático, como en la transición a la turbulencia de un líquido.
- Las trayectorias del sistema pueden parecer erráticas, como aleatorias. En estos casos puede ser necesario calcular promedios utilizando una trayectoria muy larga o muchas trayectorias diferentes. Los promedios están bien definidos para sistemas ergonódicos y se ha elaborado un entendimiento más detallado para sistemas hiperbólicos. Comprender los aspectos probabilísticos de los sistemas dinámicos ha ayudado a establecer las bases de la mecánica estadística y del caos.
Historia
Mucha gente considera al matemático francés Henri Poincaré como el fundador de los sistemas dinámicos. Poincaré publicó dos monografías ahora clásicas, "Nuevos métodos de mecánica celeste" (1892–1899) y "Conferencias sobre mecánica celeste" (1905-1910). En ellos, aplicó con éxito los resultados de su investigación al problema del movimiento de tres cuerpos y estudió en detalle el comportamiento de las soluciones (frecuencia, estabilidad, asintótica, etc.). Estos artículos incluían el teorema de recurrencia de Poincaré, que establece que ciertos sistemas, después de un tiempo suficientemente largo pero finito, volverán a un estado muy cercano al estado inicial.
Aleksandr Lyapunov desarrolló muchos métodos de aproximación importantes. Sus métodos, que desarrolló en 1899, permiten definir la estabilidad de conjuntos de ecuaciones diferenciales ordinarias. Creó la teoría moderna de la estabilidad de un sistema dinámico.
En 1913, George David Birkhoff demostró el 'último teorema geométrico' de Poincaré, un caso especial del problema de los tres cuerpos, un resultado que lo hizo mundialmente famoso. En 1927, publicó sus Sistemas dinámicos. El resultado más duradero de Birkhoff ha sido su descubrimiento en 1931 de lo que ahora se llama el teorema ergódico. Combinando conocimientos de la física sobre la hipótesis ergódica con la teoría de la medida, este teorema resolvió, al menos en principio, un problema fundamental de la mecánica estadística. El teorema ergódico también ha tenido repercusiones para la dinámica.
Stephen Smale también hizo avances significativos. Su primera contribución fue la herradura de Smale que impulsó una importante investigación en sistemas dinámicos. También describió un programa de investigación llevado a cabo por muchos otros.
Oleksandr Mykolaiovych Sharkovsky desarrolló el teorema de Sharkovsky sobre los períodos de sistemas dinámicos discretos en 1964. Una de las implicaciones del teorema es que si un sistema dinámico discreto en la línea real tiene un punto periódico de período 3, entonces debe tener puntos periódicos de cada otro período.
A fines del siglo XX, la perspectiva del sistema dinámico para las ecuaciones diferenciales parciales comenzó a ganar popularidad. El ingeniero mecánico palestino Ali H. Nayfeh aplicó dinámicas no lineales en sistemas mecánicos y de ingeniería. Su trabajo pionero en dinámica no lineal aplicada ha influido en la construcción y el mantenimiento de máquinas y estructuras que son comunes en la vida cotidiana, como barcos, grúas, puentes, edificios, rascacielos, motores a reacción, motores de cohetes, aeronaves y naves espaciales.
Definición formal
En el sentido más general, un sistema dinámico es una tupla (T, X, Φ) donde T es un monoide, escrito de forma aditiva, X es un conjunto no vacío y Φ es una función
- CCPR CCPR :U⊆ ⊆ ()T× × X)→ → X{displaystyle Phi:Usubseteq (Ttimes X)to X}
con
- proj2()U)=X{displaystyle mathrm {proj} _{2}(U)=X} (donde) proj2{displaystyle mathrm {proj} ¿Qué? es el segundo mapa de proyección)
y para cualquier x en X:
- CCPR CCPR ()0,x)=x{displaystyle Phi (0,x)=x}
- CCPR CCPR ()t2,CCPR CCPR ()t1,x))=CCPR CCPR ()t2+t1,x),{displaystyle Phi (t_{2},Phi (t_{1},x)=Phi (t_{2}+t_{1},x),}
para t1,t2+t1▪ ▪ I()x){displaystyle ,t_{1},,t_{2}+t_{1}in I(x)} y t2▪ ▪ I()CCPR CCPR ()t1,x)){displaystyle t_{2}in I(Phi (t_{1},x)}, donde hemos definido el conjunto I()x):={}t▪ ▪ T:()t,x)▪ ▪ U}{displaystyle I(x):={tin T:(t,x)in U} para cualquier x dentro X.
En particular, en el caso de que U=T× × X{displaystyle U=Ttimes X} tenemos por todos x dentro X que I()x)=T{displaystyle I(x)=T} y por lo tanto, que ⋅ define una acción monoide T on X.
La función Φ(t,x) se denomina función de evolución del sistema dinámico: se asocia a todo punto x en el conjunto X una imagen única, en función de la variable t, denominada parámetro de evolución. X se denomina espacio de fase o espacio de estado, mientras que la variable x representa un estado inicial del sistema.
A menudo escribimos
- CCPR CCPR x()t)↑ ↑ CCPR CCPR ()t,x){displaystyle Phi _{x}(t)equiv Phi (t,x)}
- CCPR CCPR t()x)↑ ↑ CCPR CCPR ()t,x){displaystyle Phi ^{t}(x)equiv Phi (t,x)}
si tomamos una de las variables como constante.
- CCPR CCPR x:I()x)→ → X{displaystyle Phi _{x}:I(x)to X}
se denomina flujo a través de x y su gráfico trayectoria a través de x. El conjunto
- γ γ x↑ ↑ {}CCPR CCPR ()t,x):t▪ ▪ I()x)}{displaystyle gamma _{x}equiv {phi (t,x):tin I(x)}
se llama la órbita a través de x. Tenga en cuenta que la órbita a través de x es la imagen del flujo a través de x. Un subconjunto S del espacio de estado X se llama Φ-invariante si para todo x en S y todo t en T
- CCPR CCPR ()t,x)▪ ▪ S.{displaystyle Phi (t,x)in S.}
Así, en particular, si S ⋅-invariable, I()x)=T{displaystyle I(x)=T} para todos x dentro S. Es decir, el flujo a través de x debe definirse para todo el tiempo por cada elemento S.
Más comúnmente, hay dos clases de definiciones para un sistema dinámico: una está motivada por ecuaciones diferenciales ordinarias y tiene un sabor geométrico; y el otro está motivado por la teoría ergódica y tiene un sabor teórico de la medida.
Definición geométrica
En la definición geométrica, un sistema dinámico es el tuple .. T,M,f.. {displaystyle langle {Mathcal {T}, {fnMitcal {},frangle }. T{displaystyle {fnMithcal}} es el dominio por el tiempo – hay muchas opciones, generalmente los reales o los enteros, posiblemente restringidos a ser no negativo. M{displaystyle {fnMithcal}} es un múltiple, es decir, localmente un espacio de Banach o Euclidean, o en el caso discreto un gráfico. f es una regla de evolución t→ft (con t▪ ▪ T{displaystyle tin {fnMithcal}. ft es un diffeomorfismo del doble a sí mismo. Así que, f es un mapeo "smooth" del tiempo-dominio T{displaystyle {fnMithcal}} en el espacio de las diffeomorfismos del doble a sí mismo. En otros términos, f()t) es un diffeomorfismo, por cada vez t en el dominio T{displaystyle {fnMithcal}}.
Sistema dinámico real
Un sistema dinámico real, sistema dinámico en tiempo real, sistema dinámico en tiempo continuo o flujo es una tupla (T, M, Φ) con T un intervalo abierto en los números reales R, M una variedad localmente difeomorfa a un espacio de Banach, y Φ una función continua. Si Φ es continuamente diferenciable, decimos que el sistema es un sistema dinámico diferenciable. Si la variedad M es localmente difeomorfa a Rn, el sistema dinámico es de dimensión finita; si no, el sistema dinámico es de dimensión infinita. Tenga en cuenta que esto no asume una estructura simpléctica. Cuando T se toma como los reales, el sistema dinámico se llama global o un flujo; y si T se restringe a los reales no negativos, entonces el sistema dinámico es un semi-flujo.
Sistema dinámico discreto
Un sistema dinámico discreto, sistema dinámico en tiempo discreto es una tupla (T, M, Φ), donde M es una variedad localmente difeomorfa a un espacio de Banach, y Φ es una función. Cuando T se toma como los números enteros, es una cascada o un mapa. Si T está restringido a los números enteros no negativos, llamamos al sistema una semi-cascada.
Autómata celular
Un autómata celular es una tupla (T, M, Φ), con T una red tal como los enteros o una cuadrícula de enteros de mayor dimensión, M es un conjunto de funciones desde una red de enteros (nuevamente, con una o más dimensiones) hasta un conjunto finito, y Φ una evolución (definida localmente) función. Como tales, los autómatas celulares son sistemas dinámicos. La red en M representa el "espacio" entramado, mientras que el de T representa el "tiempo" enrejado.
Generalización multidimensional
Los sistemas dinámicos generalmente se definen sobre una sola variable independiente, considerada como tiempo. Una clase más general de sistemas se define sobre múltiples variables independientes y, por lo tanto, se denominan sistemas multidimensionales. Dichos sistemas son útiles para el modelado, por ejemplo, el procesamiento de imágenes.
Compactación de un sistema dinámico
Dado un sistema dinámico global (R, X, Φ) en un espacio topológico de Hausdorff localmente compacto X, a menudo es útil estudiar la extensión continua Φ* de Φ hasta la compactación en un punto X* de X. Aunque perdemos la estructura diferencial del sistema original, ahora podemos usar argumentos de compacidad para analizar el nuevo sistema (R, X*, Φ*).
En los sistemas dinámicos compactos, el conjunto límite de cualquier órbita es no vacío, compacto y simplemente conectado.
Medida definición teórica
Un sistema dinámico puede definirse formalmente como una transformación de la medida reservada de un espacio de medida, el triplete (T, (X, μ), ⋅). Aquí, T es un monoide (normalmente los enteros no negativos), X es un conjunto, y (X, μ) es un espacio de probabilidad, lo que significa que la X y μ es una medida finita en (X,. A map VIEW: X → X se dice que se puede medir si, y sólo si, por cada σ en la ciudad, uno tiene CCPR CCPR − − 1σ σ ▪ ▪ .. {displaystyle Phi ^{-1}sigma in Sigma }. Se dice que hay un mapa ⋅ preservar la medida si y sólo si, por cada σ en la μ μ ()CCPR CCPR − − 1σ σ )=μ μ ()σ σ ){displaystyle mu (Phi ^{-1}sigma)=mu (sigma)}. Combinando lo anterior, se dice que un mapa ⋅ es un transformación de la medida y la conservación X , si es un mapa de X para sí mismo, es la bah-measurable, y es la conservación de medidas. El tripleteT, (X, μ), Ё), para tal Ё, se define entonces como un sistema dinámico.
El mapa ⋅ encarna la evolución del tiempo del sistema dinámico. Así, para sistemas dinámicos discretos los iterates CCPR CCPR n=CCPR CCPR ∘ ∘ CCPR CCPR ∘ ∘ ⋯ ⋯ ∘ ∘ CCPR CCPR {displaystyle Phi ^{n}=Phi circ Phi circ dots circ Phi } para cada entero n son estudiados. Para sistemas dinámicos continuos, el mapa Ё se entiende como un mapa de evolución del tiempo finito y la construcción es más complicada.
Relación con la definición geométrica
La definición teórica de medida asume la existencia de una transformación que conserva la medida. Se pueden asociar muchas medidas invariantes diferentes a cualquier regla de evolución. Si el sistema dinámico viene dado por un sistema de ecuaciones diferenciales se debe determinar la medida adecuada. Esto dificulta el desarrollo de la teoría ergódica a partir de ecuaciones diferenciales, por lo que resulta conveniente tener una definición motivada por sistemas dinámicos dentro de la teoría ergódica que eluda la elección de la medida y asuma que se ha hecho la elección. Una construcción simple (a veces llamada teorema de Krylov-Bogolyubov) muestra que para una gran clase de sistemas siempre es posible construir una medida para hacer de la regla de evolución del sistema dinámico una transformación que conserva la medida. En la construcción se suma una medida dada del espacio de estados para todos los puntos futuros de una trayectoria, asegurando la invariancia.
Algunos sistemas tienen una medida natural, como la medida de Liouville en los sistemas hamiltonianos, elegida sobre otras medidas invariantes, como las medidas sustentadas en órbitas periódicas del sistema hamiltoniano. Para los sistemas disipativos caóticos, la elección de la medida invariante es técnicamente más desafiante. La medida debe apoyarse en el atractor, pero los atractores tienen una medida de Lebesgue cero y las medidas invariantes deben ser singulares con respecto a la medida de Lebesgue. Una pequeña región del espacio de fase se contrae con la evolución del tiempo.
Para los sistemas dinámicos hiperbólicos, las medidas de Sinai-Ruelle-Bowen parecen ser la elección natural. Se construyen sobre la estructura geométrica de variedades estables e inestables del sistema dinámico; se comportan físicamente bajo pequeñas perturbaciones; y explican muchas de las estadísticas observadas de los sistemas hiperbólicos.
Construcción de sistemas dinámicos
El concepto de evolución en el tiempo es fundamental para la teoría de sistemas dinámicos como se vio en las secciones anteriores: la razón básica de este hecho es que la motivación inicial de la teoría fue el estudio del tiempo comportamiento de los sistemas mecánicos clásicos. Pero un sistema de ecuaciones diferenciales ordinarias debe resolverse antes de que se convierta en un sistema dinámico. Por ejemplo, considere un problema de valor inicial como el siguiente:
- xÍ Í =v()t,x){fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft Sans Serif}}}
- xSilenciot=0=x0{displaystyle {boldsymbol {x}vivir_{t=0}={boldsymbol {x}_{0}
dónde
- xÍ Í {displaystyle {dot {fnK}} representa la velocidad del punto de material x
- M es un manifold dimensional finito
- v: T × M → TM es un campo vectorial en Rn o Cn y representa el cambio de velocidad inducido por las fuerzas conocidas actuando en el punto material dado en el espacio de fase M. El cambio no es un vector en el espacio de faseM, pero está en el espacio tangente TM.
No hay necesidad de derivadas de orden superior en la ecuación, ni del parámetro t en v(t,x ), porque estos pueden eliminarse considerando sistemas de dimensiones superiores.
Dependiendo de las propiedades de este campo vectorial, el sistema mecánico se llama
- autónomo, cuando v()t, x) v()x)
- homogénea cuando v()t, 0) = 0 para todos t
La solución se puede encontrar usando técnicas ODE estándar y se denota como la función de evolución ya presentada anteriormente
- x()t)=CCPR CCPR ()t,x0){displaystyle {boldsymbol {x}(t)=Phi (t,{boldsymbol {x}_{0}}}}
El sistema dinámico es entonces (T, M, Φ).
Alguna manipulación formal del sistema de ecuaciones diferenciales que se muestra arriba da una forma más general de ecuaciones que un sistema dinámico debe satisfacer
- xÍ Í − − v()t,x)=0.. G()t,CCPR CCPR ()t,x0))=0{displaystyle {dot {fnfnMicrosoft Sans Serif} {x}}-{boldsymbol {v}(t,{boldsymbol {x})=0qquad Leftrightarrow qquad {mathfrak {G}left(t,Phi (t,{boldsymbol {x}_{0})right)=0}
Donde G:()T× × M)M→ → C{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}tomathbf {C} es un funcional del conjunto de funciones de evolución al campo de los números complejos.
Esta ecuación es útil cuando se modelan sistemas mecánicos con restricciones complicadas.
Muchos de los conceptos de los sistemas dinámicos se pueden extender a variedades de dimensión infinita, aquellas que son espacios de Banach localmente, en cuyo caso las ecuaciones diferenciales son ecuaciones diferenciales parciales.
Ejemplos
- Mapa del gato de Arnold
- El mapa de Baker es un ejemplo de un mapa lineal caótico
- Billares y billares externos
- Rebotando dinámicas de bolas
- Mapa del círculo
- Complejo polinomio cuadrático
- Péndulo doble
- Transformación Dyadic
- Hénon mapa
- Rotación profesional
- Kaplan-Yorke mapa
- Lista de mapas caóticos
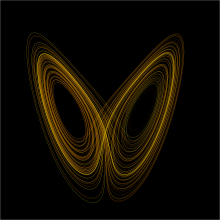
- Sistema Lorenz
- Sistema de simulación de mapas cuadráticos
- Mapa de Rössler
- Swinging Atwood's machine
- Mapa de la tienda
Sistemas dinámicos lineales
Los sistemas dinámicos lineales se pueden resolver en términos de funciones simples y el comportamiento de todas las órbitas clasificadas. En un sistema lineal, el espacio de fase es el espacio euclidiano N-dimensional, por lo que cualquier punto en el espacio de fase puede representarse mediante un vector con N números. El análisis de los sistemas lineales es posible porque cumplen un principio de superposición: si u(t) y w(t) satisfacen la ecuación diferencial para el campo vectorial (pero no necesariamente la condición inicial), entonces u(t) + w(t).
Flujos
Para un flujo, el campo vectorial v(x) es una función afín de la posición en el espacio de fase, es decir,
- xÍ Í =v()x)=Ax+b,{displaystyle {dot {x}=v(x)=Ax+b,}
con A una matriz, b un vector de números y x el vector de posición. La solución a este sistema se puede encontrar utilizando el principio de superposición (linealidad). El caso b ≠ 0 con A = 0 es solo una línea recta en la dirección de b:
- CCPR CCPR t()x1)=x1+bt.{displaystyle Phi ^{t}(x_{1})=x_{1}+bt.}
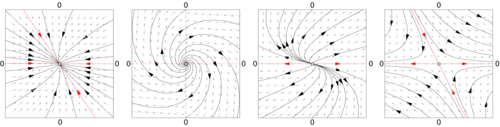
Cuando b es cero y A ≠ 0 el origen es un punto de equilibrio (o singular) del flujo, es decir, si x0 = 0, entonces la órbita permanece ahí. Para otras condiciones iniciales, la ecuación de movimiento viene dada por la exponencial de una matriz: para un punto inicial x0,
- CCPR CCPR t()x0)=etAx0.{displaystyle Phi ^{t}(x_{0})=e^{tA}x_{0}
Cuando b = 0, los valores propios de A determinan la estructura del espacio de fase. A partir de los valores propios y los vectores propios de A es posible determinar si un punto inicial convergerá o divergirá hacia el punto de equilibrio en el origen.
La distancia entre dos condiciones iniciales diferentes en el caso A ≠ 0 cambiará exponencialmente en la mayoría de los casos, ya sea convergiendo exponencialmente rápido hacia un punto o divergiendo exponencialmente rápido. Los sistemas lineales muestran una dependencia sensible de las condiciones iniciales en caso de divergencia. Para los sistemas no lineales, esta es una de las condiciones (necesarias pero no suficientes) para el comportamiento caótico.
Mapas
Un sistema dinámico afín de tiempo discreto tiene la forma de una ecuación matricial en diferencias:
- xn+1=Axn+b,{displaystyle x_{n+1}=Ax_{n}+b,}
con A una matriz y b un vector. Como en el caso continuo, el cambio de coordenadas x → x + (1 − A) –1b elimina el término b de la ecuación. En el nuevo sistema de coordenadas, el origen es un punto fijo del mapa y las soluciones son del sistema lineal A nx 0. Las soluciones para el mapa ya no son curvas, sino puntos que saltan en el espacio de fases. Las órbitas están organizadas en curvas, o fibras, que son conjuntos de puntos que se mapean en sí mismos bajo la acción del mapa.
Como en el caso continuo, los valores y vectores propios de A determinan la estructura del espacio de fase. Por ejemplo, si u1 es un vector propio de A, con un valor propio real menor que uno, entonces las líneas rectas dadas por los puntos a lo largo α u1, con α ∈ R, es una curva invariante de la mapa. Los puntos en esta línea recta se encuentran con el punto fijo.
También hay muchos otros sistemas dinámicos discretos.
Dinámica local
Las propiedades cualitativas de los sistemas dinámicos no cambian bajo un cambio suave de coordenadas (esto a veces se toma como una definición de cualitativo): un punto singular del campo vectorial (un punto donde v(x) = 0) seguirá siendo un punto singular bajo transformaciones suaves; una órbita periódica es un bucle en el espacio de fase y las deformaciones suaves del espacio de fase no pueden alterar que sea un bucle. Es en la vecindad de los puntos singulares y las órbitas periódicas donde se puede entender bien la estructura de un espacio de fase de un sistema dinámico. En el estudio cualitativo de los sistemas dinámicos, el enfoque es mostrar que hay un cambio de coordenadas (generalmente no especificado, pero computable) que hace que el sistema dinámico sea lo más simple posible.
Rectificación
Un flujo en la mayoría de los parches pequeños del espacio de fase se puede hacer muy simple. Si y es un punto donde el campo vectorial v(y) ≠ 0, entonces hay un cambio de coordenadas para una región alrededor de y donde el campo vectorial se convierte en una serie de vectores paralelos de la misma magnitud. Esto se conoce como el teorema de rectificación.
El teorema de rectificación dice que lejos de los puntos singulares, la dinámica de un punto en un pequeño parche es una línea recta. A veces, el parche se puede ampliar uniendo varios parches, y cuando esto funciona en todo el espacio de fase M, el sistema dinámico es integrable. En la mayoría de los casos, el parche no se puede extender a todo el espacio de fase. Puede haber puntos singulares en el campo vectorial (donde v(x) = 0); o los parches pueden volverse cada vez más pequeños a medida que se acerca a algún punto. La razón más sutil es una restricción global, donde la trayectoria comienza en un parche y después de visitar una serie de otros parches regresa al original. Si la próxima vez que la órbita gira alrededor del espacio de fase de una manera diferente, entonces es imposible rectificar el campo vectorial en toda la serie de parches.
Cerca de órbitas periódicas
En general, en la vecindad de una órbita periódica no se puede usar el teorema de rectificación. Poincaré desarrolló un enfoque que transforma el análisis cerca de una órbita periódica al análisis de un mapa. Elija un punto x0 en la órbita γ y considere los puntos en el espacio de fase en esa vecindad que son perpendiculares a v(x 0). Estos puntos son una sección de Poincaré S(γ, x0), de la órbita. El flujo ahora define un mapa, el mapa de Poincaré F: S → S, para puntos que comienzan en S y volviendo a S. No todos estos puntos tardarán el mismo tiempo en volver, pero los tiempos serán cercanos al tiempo que tarda x0.
La intersección de la órbita periódica con la sección de Poincaré es un punto fijo del mapa de Poincaré F. Mediante una traslación, se puede suponer que el punto está en x = 0. La serie de Taylor del mapa es F(x) = J · x + O(x2), por lo que un cambio de coordenadas h solo se puede esperar que simplifique F a su parte lineal
- h− − 1∘ ∘ F∘ ∘ h()x)=J⋅ ⋅ x.{displaystyle h^{-1}circ Fcirc h(x)=Jcdot x.}
Esto se conoce como la ecuación de conjugación. Encontrar las condiciones para que esta ecuación se cumpla ha sido una de las principales tareas de investigación en sistemas dinámicos. Poincaré lo abordó por primera vez asumiendo que todas las funciones eran analíticas y en el proceso descubrió la condición no resonante. Si λ1,..., λν son los valores propios de J serán resonantes si un valor propio es una combinación lineal entera de dos o más de los otros. Como términos de la forma λi – Σ (múltiplos de otros valores propios) aparece en el denominador de los términos de la función h , la condición no resonante también se conoce como el problema del pequeño divisor.
Resultados de conjugación
Los resultados sobre la existencia de una solución a la ecuación de conjugación dependen de los valores propios de J y del grado de suavidad requerido de h. Como J no necesita tener ninguna simetría especial, sus valores propios serán típicamente números complejos. Cuando los valores propios de J no están en el círculo unitario, la dinámica cerca del punto fijo x0 de F se llama hiperbólica y cuando los valores propios están en el círculo unitario y complejo, la dinámica se llama elíptica.
En el caso hiperbólico, el teorema de Hartman-Grobman da las condiciones para la existencia de una función continua que mapea la vecindad del punto fijo del mapa al mapa lineal J · x. El caso hiperbólico también es estructuralmente estable. Pequeños cambios en el campo vectorial solo producirán pequeños cambios en el mapa de Poincaré y estos pequeños cambios se reflejarán en pequeños cambios en la posición de los valores propios de J en el plano complejo, lo que implica que el mapa sigue siendo hiperbólico.
El teorema de Kolmogorov-Arnold-Moser (KAM) proporciona el comportamiento cerca de un punto elíptico.
Teoría de la bifurcación
Cuando el mapa de evolución Φt (o el campo vectorial del que se deriva) depende de un parámetro μ, la estructura del espacio de fases también dependerá de este parámetro. Los pequeños cambios pueden no producir cambios cualitativos en el espacio de fase hasta que se alcanza un valor especial μ0. En este punto, el espacio de fases cambia cualitativamente y se dice que el sistema dinámico ha pasado por una bifurcación.
La teoría de la bifurcación considera una estructura en el espacio de fase (normalmente un punto fijo, una órbita periódica o un toroide invariable) y estudia su comportamiento en función del parámetro μ. En el punto de bifurcación, la estructura puede cambiar su estabilidad, dividirse en nuevas estructuras o fusionarse con otras estructuras. Mediante el uso de aproximaciones de la serie de Taylor de los mapas y la comprensión de las diferencias que pueden eliminarse mediante un cambio de coordenadas, es posible catalogar las bifurcaciones de los sistemas dinámicos.
Las bifurcaciones de un punto fijo hiperbólico x0 de una familia de sistemas Fμ se pueden caracterizar por los valores propios de la primera derivada del sistema DFμ(x0) calculado en el punto de bifurcación. Para un mapa, la bifurcación ocurrirá cuando haya valores propios de DFμ en el círculo unitario. Para un flujo, ocurrirá cuando haya valores propios en el eje imaginario. Para obtener más información, consulte el artículo principal sobre la teoría de la bifurcación.
Algunas bifurcaciones pueden dar lugar a estructuras muy complicadas en el espacio de fase. Por ejemplo, el escenario de Ruelle-Takens describe cómo una órbita periódica se bifurca en un toro y el toro en un atractor extraño. En otro ejemplo, la duplicación del período de Feigenbaum describe cómo una órbita periódica estable atraviesa una serie de bifurcaciones de duplicación del período.
Sistemas ergódicos
En muchos sistemas dinámicos, es posible elegir las coordenadas del sistema para que el volumen (realmente un volumen ν-dimensional) en el espacio de fases sea invariable. Esto sucede para los sistemas mecánicos derivados de las leyes de Newton siempre que las coordenadas sean la posición y el momento y el volumen se mida en unidades de (posición) × (momento). El flujo toma puntos de un subconjunto A en los puntos Φ t(A) y la invariancia del espacio de fase significa que
- vol()A)=vol()CCPR CCPR t()A)).{displaystyle mathrm {vol} (A)=mathrm {vol} (Phi ^{t}(A)). }
En el formalismo hamiltoniano, dada una coordenada, es posible derivar el impulso apropiado (generalizado) de modo que el flujo conserve el volumen asociado. Se dice que el volumen se calcula con la medida de Liouville.
En un sistema hamiltoniano, no todas las configuraciones posibles de posición y momento pueden alcanzarse a partir de una condición inicial. Debido a la conservación de la energía, solo son accesibles los estados con la misma energía que la condición inicial. Los estados con la misma energía forman una capa de energía Ω, una subvariedad del espacio de fase. El volumen de la capa de energía, calculado usando la medida de Liouville, se conserva bajo evolución.
Para los sistemas en los que el flujo conserva el volumen, Poincaré descubrió el teorema de recurrencia: suponga que el espacio de fase tiene un volumen de Liouville finito y sea F un mapa de espacio de fase que conserva el volumen y A un subconjunto del espacio de fases. Luego, casi todos los puntos de A vuelven a A infinitamente a menudo. Zermelo utilizó el teorema de recurrencia de Poincaré para oponerse a la derivación de Boltzmann del aumento de entropía en un sistema dinámico de átomos en colisión.
Una de las cuestiones planteadas por el trabajo de Boltzmann fue la posible igualdad entre las medias temporales y las medias espaciales, lo que él denominó hipótesis ergódica. La hipótesis establece que el tiempo que una trayectoria típica pasa en una región A es vol(A)/vol(Ω).
La hipótesis ergódica resultó no ser la propiedad esencial necesaria para el desarrollo de la mecánica estadística y se introdujeron una serie de otras propiedades similares a las ergódicas para capturar los aspectos relevantes de los sistemas físicos. Koopman se acercó al estudio de los sistemas ergódicos mediante el uso del análisis funcional. Un a observable es una función que a cada punto del espacio fase le asocia un número (digamos presión instantánea, o altura media). El valor de un observable se puede calcular en otro momento mediante la función de evolución φ t. Esto introduce un operador U t, el operador de transferencia,
- ()Uta)()x)=a()CCPR CCPR − − t()x)).{displaystyle (U^{t}a)(x)=a(Phi ^{-t}(x)). }
Al estudiar las propiedades espectrales del operador lineal U es posible clasificar las propiedades ergódicas de Φ t. Al utilizar el enfoque de Koopman de considerar la acción del flujo en una función observable, el problema no lineal de dimensión finita que implica Φ t se transforma en un problema lineal de dimensión infinita que implica U.
La medida de Liouville restringida a la superficie de energía Ω es la base para los promedios calculados en mecánica estadística de equilibrio. Un promedio en el tiempo a lo largo de una trayectoria es equivalente a un promedio en el espacio calculado con el factor de Boltzmann exp(−βH). Esta idea ha sido generalizada por Sinai, Bowen y Ruelle (SRB) a una clase más amplia de sistemas dinámicos que incluye sistemas disipativos. Las medidas SRB reemplazan el factor de Boltzmann y se definen sobre atractores de sistemas caóticos.
Sistemas dinámicos no lineales y caos
Los sistemas dinámicos no lineales simples e incluso los sistemas lineales por partes pueden exhibir un comportamiento completamente impredecible, que puede parecer aleatorio, a pesar de que son fundamentalmente deterministas. Este comportamiento aparentemente impredecible se ha denominado caos. Los sistemas hiperbólicos son sistemas dinámicos definidos con precisión que exhiben las propiedades atribuidas a los sistemas caóticos. En los sistemas hiperbólicos el espacio tangente perpendicular a una trayectoria se puede separar bien en dos partes: una con los puntos que convergen hacia la órbita (la variedad estable) y otra con los puntos que divergen de la órbita (la variedad inestable).
Esta rama de las matemáticas se ocupa del comportamiento cualitativo a largo plazo de los sistemas dinámicos. Aquí, el enfoque no está en encontrar soluciones precisas a las ecuaciones que definen el sistema dinámico (que a menudo no tiene remedio), sino en responder preguntas como "¿Se establecerá el sistema en un estado estable a largo plazo, y si entonces, ¿cuáles son los posibles atractores?" o "¿El comportamiento a largo plazo del sistema depende de su condición inicial?"
Tenga en cuenta que el comportamiento caótico de los sistemas complejos no es el problema. Se sabe desde hace años que la meteorología implica un comportamiento complejo, incluso caótico. La teoría del caos ha sido tan sorprendente porque el caos se puede encontrar dentro de sistemas casi triviales. El mapa logístico es solo un polinomio de segundo grado; el mapa de herradura es lineal por partes.
Soluciones de duración finita
Para las EDO autónomas no lineales, es posible, bajo algunas condiciones, desarrollar soluciones de duración finita, lo que significa que, a partir de su propia dinámica, el sistema alcanzará el valor cero en un tiempo final y permanecerá allí en cero para siempre. Estas soluciones de duración finita no pueden ser funciones analíticas en toda la línea real, y debido a que serán funciones que no sean de Lipschitz en su tiempo final, no soportan la unicidad de las soluciones de las ecuaciones diferenciales de Lipschitz.
Como ejemplo, la ecuación:
- Sí..=− − Sgn()Sí.)SilencioSí.Silencio,Sí.()0)=1{displaystyle y'=-{text{sgn}(y){sqrt ¿Qué?
Admite la solución de duración finita:
- Sí.()x)=14()1− − x2+Silencio1− − x2Silencio)2{displaystyle y(x)={4}left(1-{frac] {x}{2}+left habit1-{frac {x}{2}right sobre la vidaright)} {2}}
Contenido relacionado
Notación cientifica
Profesor Lucasiano de Matemáticas
Centro (teoría de grupos)