Sistema de Trachtenberg

El sistema Trachtenberg es un sistema de cálculo mental rápido. El sistema consta de una serie de operaciones fácilmente memorizables que permiten realizar cálculos aritméticos muy rápidamente. Fue desarrollado por el ingeniero ruso Jakow Trachtenberg para mantener su mente ocupada mientras se encontraba en un campo de concentración nazi.

El resto de este artículo presenta algunos métodos ideados por Trachtenberg. Algunos de los algoritmos que desarrolló Trachtenberg son los de multiplicación, división y suma generales. Además, el sistema Trachtenberg incluye algunos métodos especializados para multiplicar números pequeños entre 5 y 13 (pero aquí se muestra del 2 al 12).

La sección sobre suma demuestra un método eficaz para verificar cálculos que también se puede aplicar a la multiplicación.

Multiplicación general

El método para la multiplicación general es un método para lograr multiplicaciones ${displaystyle atimes b}$ con baja complejidad espacial, es decir, tan pocos resultados temporales como sea posible para mantenerse en memoria. Esto se logra notando que el dígito final está completamente determinado multiplicando el último dígito de los multiplicandos. Esto se considera un resultado temporal. Para encontrar el próximo dígito último, necesitamos todo lo que influye en este dígito: El resultado temporal, el último dígito de ${displaystyle a}$ el siguiente dígito al último ${displaystyle b}$, así como el siguiente dígito a último ${displaystyle a}$ tiempos el último dígito ${displaystyle b}$. Este cálculo se realiza, y tenemos un resultado temporal que es correcto en los dos dígitos finales.

En general, para cada posición ${displaystyle n}$ en el resultado final, sumamos para todos ${displaystyle i}$:

${displaystyle a{text{ (digit at }i{text{)}times b{text{ (digit at } {-n-i){text{)}}}$

Las personas pueden aprender este algoritmo y así multiplicar mentalmente números de cuatro dígitos, anotando sólo el resultado final. Lo escribirían comenzando con el dígito más a la derecha y terminando con el más a la izquierda.

Trachtenberg definió este algoritmo con una especie de multiplicación por pares donde dos dígitos se multiplican por un dígito, esencialmente manteniendo solo el dígito central del resultado. Al realizar el algoritmo anterior con esta multiplicación por pares, es necesario conservar aún menos resultados temporales.

Ejemplo: ${displaystyle 123456times 789}$

Para encontrar el primer dígito (el más a la derecha) de la respuesta, comience en el primer dígito del multiplicando

El dígito de unidades ${displaystyle 9times 6}$ es ${displaystyle 4.$

El primer dígito de la respuesta es ${displaystyle 4}$. Los diez dígitos ${displaystyle 5}$ es ignorado.

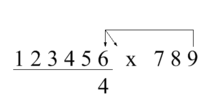
Para encontrar el segundo dígito de la respuesta, comience en el segundo dígito del multiplicando:

El dígito de unidades ${displaystyle 9times 5}$ más el diez dígitos de ${displaystyle 9times 6}$ más

El dígito de unidades ${displaystyle 8times 6}$.

${displaystyle 5+5+8=18}$.

El segundo dígito de la respuesta es ${displaystyle 8}$ y carga ${displaystyle 1}$ al tercer dígito.

Para encontrar el tercer dígito de la respuesta, comience en el tercer dígito del multiplicando:

El dígito de unidades ${displaystyle 9times 4}$ más el diez dígitos de ${displaystyle 9times 5}$ más

El dígito de unidades ${displaystyle 8times 5}$ más el diez dígitos de ${displaystyle 8times 6}$ más

El dígito de unidades ${displaystyle 7times 6}$

${displaystyle 1+6+4+0+4+2=17}$

El tercer dígito de la respuesta es ${displaystyle 7}$ y carga ${displaystyle 1}$ al siguiente dígito.

Para encontrar el cuarto dígito de la respuesta, comience en el cuarto dígito del multiplicando:

El dígito de unidades ${displaystyle 9times 3}$ más el diez dígitos de ${displaystyle 9times 4}$ más

El dígito de unidades ${displaystyle 8times 4}$ más el diez dígitos de ${displaystyle 8times 5}$ más

El dígito de unidades ${displaystyle 7times 5}$ más el diez dígitos de ${displaystyle 7times 6}$.

${displaystyle 1+7+3+2+4+5+4=26}$ llevado del tercer dígito.

El cuarto dígito de la respuesta es ${displaystyle 6}$ y carga ${displaystyle 2}$ al siguiente dígito.

Continúe con el mismo método para obtener los dígitos restantes.

Trachtenberg llamó a esto el método de los 2 dedos. Los cálculos para encontrar el cuarto dígito del ejemplo anterior se ilustran a la derecha. La flecha del nueve siempre apuntará al dígito del multiplicando directamente encima del dígito de la respuesta que deseas encontrar, y las otras flechas apuntarán cada una un dígito a la derecha. Cada punta de flecha apunta a un par UT o par de productos. La flecha vertical apunta al producto donde obtendremos el dígito de las Unidades y la flecha inclinada apunta al producto donde obtendremos los dígitos de las Decenas del Par de Productos. Si una flecha apunta a un espacio sin dígitos, no hay ningún cálculo para esa flecha. A medida que resuelves cada dígito, moverás cada una de las flechas sobre el multiplicando un dígito hacia la izquierda hasta que todas las flechas apunten a ceros prefijados.

La división en el sistema Trachtenberg se realiza de forma muy similar a la multiplicación, pero con resta en lugar de suma. Dividir el dividendo en dividendos parciales más pequeños y luego dividir este dividendo parcial solo por el dígito más a la izquierda del divisor proporcionará la respuesta un dígito a la vez. A medida que resuelves cada dígito de la respuesta, restas los pares de productos (pares UT) y también los pares NT (Números-Decenas) del dividendo parcial para encontrar el siguiente dividendo parcial. Los Pares de Productos se encuentran entre los dígitos de la respuesta hasta el momento y el divisor. Si una resta da como resultado un número negativo, debes retroceder un dígito y reducir ese dígito de la respuesta en uno. Con suficiente práctica, este método se puede realizar mentalmente.

Adición general

Un método para sumar columnas de números y verificar con precisión el resultado sin repetir la primera operación. Se produce una suma intermedia, en forma de dos filas de dígitos. La respuesta se obtiene sumando los resultados intermedios con un algoritmo en forma de L. Como paso final, el método de verificación que se recomienda elimina el riesgo de repetir cualquier error original e identifica la columna precisa en la que ocurre un error de una sola vez. Se basa en sumas de cheques (o dígitos), como el método del resto de nueves.

Para que el procedimiento sea efectivo, las diferentes operaciones utilizadas en cada etapa deben mantenerse distintas, de lo contrario existe riesgo de interferencia.

Otros algoritmos de multiplicación

Al realizar cualquiera de estos algoritmos de multiplicación, se deben seguir los siguientes "pasos" debería aplicarse.

La respuesta debe encontrarse un dígito a la vez, comenzando en el dígito menos significativo y moviéndose hacia la izquierda. El último cálculo se realiza en el cero inicial del multiplicando.

Cada dígito tiene un vecino, es decir, el dígito de su derecha. El vecino del dígito más a la derecha es el cero final.

La 'mitad' La operación tiene un significado particular para el sistema Trachtenberg. Su intención es significar "la mitad del dígito, redondeado hacia abajo" pero por razones de velocidad se recomienda a las personas que siguen el sistema Trachtenberg que hagan que este proceso de reducción a la mitad sea instantáneo. Entonces, en lugar de pensar "la mitad de siete es tres y medio, entonces tres" se sugiere pensar “siete, tres”. Esto acelera considerablemente el cálculo. De esta misma forma se deben memorizar las tablas para restar cifras del 10 o del 9.

Y siempre que la regla requiera sumar la mitad del vecino, siempre suma 5 si el dígito actual es impar. Esto compensa la pérdida de 0,5 en el cálculo del siguiente dígito.

Números y dígitos (base 10)

Los dígitos y los números son dos nociones diferentes. El número T consta de n dígitos c_n... c₁.

Multiplicar por 2

Prueba

Regla:

1. Multiplique cada dígito por 2 (con carga).

Ejemplo: 8624 × 2

Trabajando de izquierda a derecha:

8+8=16,

6+6=12 (carry the 1),

2+2=4

4+4=8;

8624 × 2 = 17248

Ejemplo: 76892 × 2

Trabajando de izquierda a derecha:

7+7=14

6+6=12

8+8=16

9+9=18

2+2=4;

76892 × 2 = 153784

Multiplicar por 3

Prueba

Regla:

1. Subir el dígito más correcto de 10.
2. Subir los dígitos restantes de 9.
3. Doble el resultado.
4. Añadir la mitad del vecino a la derecha, más 5 si el dígito es extraño.
5. Para el primer cero, resta 2 de la mitad del vecino.

Ejemplo: 492 × 3 = 1476

Trabajando de derecha a izquierda:

(10 − 2) × 2 + mitad de 0 (0) = 16. Escribe 6, lleva 1.

(9 − 9) × 2 + mitad de 2 (1) + 5 (ya que 9 es raro) + 1 (carried) = 7. Escriba 7.

(9 − 4) × 2 + mitad de 9 (4) = 14. Escribe 4, lleva 1.

Medio de 4 (2) − 2 + 1 (carried) = 1. Escriba 1.

Multiplicar por 4

Prueba

Contenido relacionado