Sistema de numeración hindú-árabe

El Sistema de numeral hindú-árabe (también conocido como Sistema de numeral indorábico, Sistema de numeral hindú, Sistema de numeral árabe) es un sistema base de diez numerales para representar números enteros; su extensión a los no-integers es el sistema de numeral decimal, que es actualmente el sistema de numeral más común.
El sistema fue inventado entre los siglos I y IV por matemáticos indios. El sistema fue adoptado en las matemáticas árabes en el siglo IX. Se hizo más conocido gracias a los escritos en árabe del matemático persa Al-Khwārizmī (Sobre el cálculo con números hindúes, c. 825) y el matemático árabe Al-Kindi (Sobre el uso de los números hindúes, c. 830). El sistema se había extendido a la Europa medieval en la Alta Edad Media, especialmente después del Liber Abaci del siglo XIII de Fibonacci; Hasta la evolución de la imprenta en el siglo XV, el uso del sistema en Europa se limitaba principalmente al norte de Italia.
Se basa en diez glifos que representan los números del cero al nueve, y permite representar cualquier número natural mediante una secuencia única de estos glifos. Los símbolos (glifos) utilizados para representar el sistema son, en principio, independientes del sistema mismo. Los glifos en uso actual descienden de los números brahmi y se han dividido en varias variantes tipográficas desde la Edad Media.
Estos conjuntos de símbolos se pueden dividir en tres familias principales: números arábigos occidentales utilizados en el Gran Magreb y en Europa; Números arábigos orientales utilizados en Medio Oriente; y los números indios en diversas escrituras utilizadas en el subcontinente indio.
Orígenes
En algún momento alrededor del año 600 EC, comenzó un cambio en la escritura de fechas en las escrituras derivadas de Brāhmī de la India y el sudeste asiático, transformándose de un sistema aditivo con numerales separados para números de diferentes magnitudes a un sistema de valor posicional posicional con un un solo conjunto de glifos para el 1 al 9 y un punto para el cero, desplazando gradualmente las expresiones aditivas de números durante los siglos siguientes. Este sistema de numeración indio fue el primero en presentar la combinación de cifrado, notación posicional, cero y base decimal.
Cuando este sistema fue adoptado y extendido por los árabes y persas medievales, lo llamaron al-ḥisāb al-hindī ("aritmética india"). Estos números fueron adoptados gradualmente en Europa a partir del siglo X, probablemente transmitidos por los comerciantes árabes; Los matemáticos europeos medievales y renacentistas generalmente los reconocían como de origen indio; sin embargo, algunas fuentes influyentes los atribuyeron a los árabes y, con el tiempo, llegaron a ser conocidos generalmente como "números arábigos" (números arábigos). en Europa. Según algunas fuentes, este sistema numérico puede haberse originado en los números chinos Shang (1200 a. C.), que también era un sistema de numeración posicional decimal.
Notación posicional
El sistema hindú-árabe está diseñado para la notación posicional en un sistema decimal. En una forma más desarrollada, la notación posicional también utiliza un marcador decimal (al principio una marca sobre el dígito de las unidades, pero ahora más comúnmente un punto decimal o una coma decimal que separa las unidades de las décimas), y también un símbolo para & #34;estos dígitos se repiten ad infinitum". En el uso moderno, este último símbolo suele ser un vinculum (una línea horizontal colocada sobre los dígitos repetidos). En esta forma más desarrollada, el sistema numérico puede simbolizar cualquier número racional utilizando sólo 13 símbolos (los diez dígitos, el marcador decimal, el vinculum y un signo menos antepuesto para indicar un número negativo).
Aunque generalmente se encuentran en textos escritos con el abjad árabe ("alfabeto"), los números escritos con estos números también colocan el dígito más significativo a la izquierda, por lo que se leen de izquierda a derecha (aunque los dígitos no siempre se dicen en orden de mayor a menor). Los cambios necesarios en la dirección de lectura se encuentran en textos que combinan sistemas de escritura de izquierda a derecha con sistemas de derecha a izquierda.
Símbolos
Se utilizan varios conjuntos de símbolos para representar números en el sistema de numeración hindú-árabe, la mayoría de los cuales se desarrollaron a partir de los números Brahmi.
Los símbolos utilizados para representar el sistema se han dividido en diversas variantes tipográficas desde la Edad Media, ordenados en tres grupos principales:
- Los "números arábigos" occidentales extendidos utilizados con los alfabetos latinos, cirílicos y griegos en la tabla, descendieron de los "números árabes occidentales" que se desarrollaron en al-Andalus y el Magreb (hay dos estilos tipográficos para hacer números arábigos occidentales, conocidos como figuras de revestimiento y figuras de texto).
- Los números "árabe-indic" o "árabe oriental" utilizados con escritura árabe, desarrollados principalmente en lo que ahora es Irak. Una variante de los números arábigos orientales se utiliza en Persa y Urdu.
- Los números indios en uso con guiones de la familia Brahmic en India y el sudeste asiático. Cada uno de los principales scripts de la India tiene sus propios glifos numerales (como se notará al utilizar gráficos de caracteres Unicode).
Comparación de glifos
| Signatura | Usado con scripts | Números | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Árabe, latín, cirílico y griego | Números árabes |
| ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ | Árabe | Números árabes orientales |
| ۰ | ۱ | ۲ | ۳ | ۴ | . | . | ۷ | ۸ | ۹ | Persa / Dari / Pashto | |
| ۰ | ۱ | ۲ | ۳ | ۴ | . | . | ۷ | ۸ | ۹ | Urdu / Shahmukhi | |
| ⠚ | ⠁ | ⠃ | ⠉ | ⠙ | ⠑ | ⠋ | . | ⠓ | ⠊ | Braille | Números de braille |
| 𑁦 | 𑁧 | 𑁨 | 𑁩 | 𑁪 | 𑁫 | 𑁬 | 𑁭 | 𑁮 | 𑁯 | Brahmi | Números Brahmi |
| ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ | Devanagari | Números de devanagari |
| ௦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ | Tamil | Números Tamil |
| ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ | Eastern Nagari | Números de Bengali |
| 𐴰 | 𐴱 | 𐴲 | 𐴳 | 𐴴 | 𐴵 | 𐴶 | 𐴷 | 𐴸 | 𐴹 | Hanifi Rohingya | Hanifi Rohingya script § Números |
| ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ | Gurmukhi | Números de Gurmukhi |
| ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ | Gujarati | Números de Gujarati |
| 𑙐 | 𑙑 | 𑙒 | 𑙓 | 𑙔 | 𑙕 | 𑙖 | 𑙗 | 𑙘 | 𑙙 | Modi | Números de modi |
| 𑋰 | 𑋱 | 𑋲 | 𑋳 | 𑋴 | 𑋵 | 𑋶 | 𑋷 | 𑋸 | 𑋹 | Khudabadi | Khudabadi script § Numerals |
| ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ | Odia | Números de Odia |
| ᱐ | ᱑ | ᱒ | ᱓ | ᱔ | ᱕ | ᱖ | ᱗ | ᱘ | ᱙ | Santali | Números de Santali |
| 𑇐 | 𑇑 | 𑇒 | 𑇓 | 𑇔 | 𑇕 | 𑇖 | 𑇗 | 𑇘 | 𑇙 | Sharada | Números de Sharada |
| ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ | Telugu | Guión Telugu § Numerals |
| ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ | Kannada | Kannada script § Numerals |
| ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ | Malayalam | Números de malayalam |
| ꯰ | ꯱ | ꯲ | ꯳ | ꯴ | ꯵ | ꯶ | ꯷ | ꯸ | ꯹ | Meitei | Meitei script § Numerals |
| ෦ | ෧ | ෨ | ෩ | ෪ | ෫ | ෬ | ෭ | ෮ | ෯ | Sinhala | Números de Sinhala |
| 𑓐 | 𑓑 | 𑓒 | 𑓓 | 𑓔 | 𑓕 | 𑓖 | 𑓗 | 𑓘 | 𑓙 | Tirhuta Mithilakshar | Números Maithili |
| ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ | Tibetan | Números tibetanos |
| ᥆ | ᥇ | ᥈ | ᥉ | ᥊ | ᥋ | ᥌ | ᥍ | ᥎ | ᥏ | Limbu | Limbu script § Digits |
| ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ | Burmese | Números Birmanos |
| ᠐ | ᠑ | ᠒ | ᠓ | ᠔ | ᠕ | . | ᠗ | ᠘ | ᠙ | Mongolia | Números de Mongolia |
| ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ | Khmer | Números Khmer |
| . | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ | Tailandia | Números de Tailandia |
| ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ | Lao | Lao script § Numerals |
| ᧐ | ᧑/ | ᧒ | ᧓ | ᧔ | ᧕ | ᧖ | ᧗ | ᧘ | ᧙ | New Tai Lue | Nuevo Tai Lue script § Digits |
| ꩐ | ꩑ | ꩒ | ꩓ | ꩔ | ꩕ | ꩖ | ꩗ | ꩘ | ꩙ | Cham | Cham script § Numerals |
| 𑽐 | 𑽑 | 𑽒 | 𑽓 | 𑽔 | 𑽕 | 𑽖 | 𑽗 | 𑽘 | 𑽙 | Kawi | Kawi script § Digits |
| ꧐ | ꧑ | ꧒ | ꧓ | ꧔ | ꧕ | ꧖ | ꧗ | ꧘ | ꧙ | Javanese | Números Javaneses |
| ᭐ | ᭑ | ᭒ | ᭓ | ᭔ | ᭕ | ᭖ | ᭗ | ᭘ | ᭙ | Balinese | Números balineses |
| ᮰ | ᮱ | ᮲ | ᮳ | ᮴ | ᮵ | ᮶ | ᮷ | ᮸ | ᮹ | Sundanese | Números sundaneses |
Historia
Predecesores
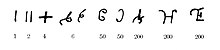
Los números Brahmi en la base del sistema son anteriores a la Era Común. Reemplazaron los primeros números Kharosthi utilizados desde el siglo IV a.C. Los números Brahmi y Kharosthi se utilizaron uno junto al otro en el período del Imperio Maurya, y ambos aparecieron en los edictos de Ashoka del siglo III a.C.

Las inscripciones budistas de alrededor de 300 BC utilizan los símbolos que se convirtieron en 1, 4 y 6. Un siglo después, se registró su uso de los símbolos que se convirtieron en 2, 4, 6, 7, y 9. Estos números Brahmi son los antepasados de los glifos hindú-árabes 1 a 9, pero no fueron utilizados como un sistema posicional con un cero, y había números bastante separados para cada uno de los diez (10, 20, 30, etc.).
El sistema numeral real, incluyendo notación posicional y uso de cero, es en principio independiente de los glifos utilizados, y significativamente más joven que los números Brahmi.
Desarrollo
El sistema de valor posicional se utiliza en el manuscrito Bakhshali; las primeras hojas datan del período 224-383 d. C. por radiocarbono. El desarrollo del sistema decimal posicional tiene su origen en las matemáticas indias durante el período Gupta. Alrededor del año 500, el astrónomo Aryabhata utiliza la palabra kha ("vacío") para marcar el "cero" en disposiciones tabulares de dígitos. El Brahmasphuta Siddhanta del siglo VII contiene una comprensión comparativamente avanzada del papel matemático del cero. La traducción sánscrita del texto cosmológico prakrit jaina perdido del siglo V Lokavibhaga puede preservar una instancia temprana de uso posicional de cero.
La primera inscripción fechada e indiscutible que muestra el uso de un símbolo para el cero aparece en una inscripción en piedra encontrada en el templo Chaturbhuja en Gwalior en India, fechada en 876.
Mundo islámico medieval
Estos avances indios se retomaron en las matemáticas islámicas en el siglo VIII, como se registra en la Cronología de los eruditos de al-Qifti (principios del siglo XIII).
En las matemáticas islámicas del siglo X, el sistema se amplió para incluir fracciones, como se registra en un tratado del matemático del califato abasí Abu'l-Hasan al-Uqlidisi, quien fue el primero en describir fracciones decimales posicionales. Según J. L. Breggren, los musulmanes fueron los primeros en representar los números como lo hacemos nosotros, ya que fueron ellos quienes inicialmente extendieron este sistema de numeración para representar partes de la unidad mediante fracciones decimales, algo que los hindúes no lograron. Por lo tanto, nos referimos al sistema como "hindú-árabe" bastante apropiadamente.
El sistema de numeración llegó a ser conocido tanto por el matemático persa Khwarizmi, que escribió un libro, Sobre el cálculo con números hindúes alrededor del año 825, como por el matemático árabe Al-Kindi, que escribió un libro, Sobre el uso de los números hindúes (كتاب في استعمال العداد الهندي [kitāb fī isti'māl al-'adād al-hindī]) alrededor del año 830. El científico persa Kushyar Gilani que escribió Kitab fi usul hisab al-hind (Principios del cálculo hindú) es uno de los manuscritos más antiguos que se conservan y utiliza números hindúes. Estos libros son los principales responsables de la difusión del sistema de numeración hindú en todo el mundo islámico y, en última instancia, también en Europa.
Adopción en Europa

En la Europa cristiana, la primera mención y representación de los números hindú-árabes (del uno al nueve, sin cero) se encuentra en el Codex Vigilanus (también conocido como Albeldensis), una recopilación iluminada de diversos documentos históricos del periodo visigodo en España, escrita en el año 976 por tres monjes. del monasterio riojano de San Martín de Albelda. Entre 967 y 969, Gerberto de Aurillac descubrió y estudió la ciencia árabe en las abadías catalanas. Posteriormente obtuvo de estos lugares el libro De multiplicatione et divisione ( Sobre multiplicación y división). Después de convertirse en Papa Silvestre II en el año 999, introdujo un nuevo modelo de ábaco, el llamado Ábaco de Gerberto, mediante la adopción de fichas que representan números hindú-árabes, del uno al nueve.
Leonardo Fibonacci trajo este sistema a Europa. Su libro Liber Abaci introdujo el Modus Indorum (el método de los indios), hoy conocido como sistema de numeración hindú-árabe o notación posicional de base 10, el uso del cero y el sistema de decimales en el mundo latino. El sistema de numeración pasó a denominarse "árabe" por los europeos. Se utilizó en las matemáticas europeas desde el siglo XII y entró en uso común a partir del siglo XV para reemplazar los números romanos.
La forma familiar de los glifos árabes occidentales tal como se usan ahora con el alfabeto latino (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) son producto de finales del siglo XV y principios del XVI. , cuando entraron en la composición tipográfica temprana. Los científicos musulmanes utilizaron el sistema de numeración babilónico y los comerciantes utilizaron los números de Abjad, un sistema similar al sistema de numeración griego y al sistema de numeración hebreo. De manera similar, la introducción del sistema por parte de Fibonacci en Europa estuvo restringida a círculos eruditos. El mérito de haber sido el primero en establecer una comprensión y un uso generalizados de la notación posicional decimal entre la población general es de Adam Ries, un autor del Renacimiento alemán, cuyo libro de 1522 Rechenung auff der linihen und federn (Calcular sobre líneas y con pluma) estaba dirigido a aprendices de empresarios y artesanos.
- Gregor Reisch, Madame Arithmatica, 1508
- Una tabla de cálculo, utilizado para aritmética utilizando números romanos
- Adam Ries, Rechenung auff der linihen und federn, 1522
- Dos libros aritméticos publicados en 1514 – Köbel (izquierda) utilizando una tabla de cálculo y Böschenteyn usando numerales
- Adam Ries, Rechenung auff der linihen und federn (2a Ed.), 1525
- Robert Recorde, El suelo de las artes, 1543
- Peter Apian, Kaufmanns Rechnung, 1527
- Adam Ries, Rechenung auff der linihen und federn (2a Ed.), 1525
Adopción en el este de Asia
En el año 690 d.C., la emperatriz Wu promulgó los caracteres zetianos, uno de los cuales era "〇". La palabra ahora se utiliza como sinónimo del número cero.
En China, Gautama Siddha introdujo los números hindúes con cero en el año 718, pero los matemáticos chinos no los encontraron útiles, ya que ya tenían las varillas de conteo posicionales decimales.
En los números chinos, se utiliza un círculo (〇) para escribir cero en los números de Suzhou. Muchos historiadores piensan que Gautama Siddha lo importó de números indios en 718, pero algunos eruditos chinos creen que fue creado a partir del relleno de espacio de texto chino "□".
Los chinos y los japoneses finalmente adoptaron los números hindú-árabes en el siglo XIX, abandonando las varillas para contar.
Propagación de la variante árabe occidental
El "árabe occidental" Los números, tal como eran de uso común en Europa desde el período barroco, han encontrado un uso secundario en todo el mundo junto con el alfabeto latino, e incluso significativamente más allá de la difusión contemporánea del alfabeto latino, introduciéndose en los sistemas de escritura en regiones donde otras variantes del alfabeto hindú. Los números arábigos se utilizaban, pero también junto con la escritura china y japonesa (ver números chinos, números japoneses).

![A calculation table [de], used for arithmetic using Roman numerals](https://upload.wikimedia.org/wikipedia/commons/thumb/e/e0/Rechentisch.png/120px-Rechentisch.png)





