Sistema de Lorenz

El sistema de Lorenz es un sistema de ecuaciones diferenciales ordinarias estudiado por primera vez por el matemático y meteorólogo Edward Lorenz. Es notable por tener soluciones caóticas para ciertos valores de parámetros y condiciones iniciales. En particular, el atractor de Lorenz es un conjunto de soluciones caóticas del sistema de Lorenz. El término "efecto mariposa" en los medios populares puede provenir de las implicaciones del mundo real del atractor de Lorenz, es decir, que pequeños cambios en las condiciones iniciales evolucionan hacia trayectorias completamente diferentes. Esto subraya que los sistemas caóticos pueden ser completamente deterministas y, sin embargo, ser inherentemente imprácticos o incluso imposibles de predecir durante períodos de tiempo más largos. Por ejemplo, incluso el pequeño aleteo de las alas de una mariposa podría hacer que la atmósfera de la Tierra siga una trayectoria muy diferente, en la que, por ejemplo, se produce un huracán donde de otra manera no se habría producido (ver puntos de silla). La forma del propio atractor de Lorenz, cuando se representa gráficamente en el espacio de fases, también puede parecerse a una mariposa.

En 1963, Edward Lorenz, con la ayuda de Ellen Fetter, responsable de las simulaciones numéricas y las figuras, y de Margaret Hamilton, que colaboró en los cálculos numéricos iniciales que condujeron a los hallazgos del modelo de Lorenz, desarrolló un modelo matemático simplificado para la convección atmosférica. El modelo es un sistema de tres ecuaciones diferenciales ordinarias conocidas actualmente como ecuaciones de Lorenz:

${\fnMicrosoft Sans Serif} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrom {\f} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\f} {\f}\fnMicrosoft}\fnMicrosoft}}\f}\f}\f}\f}\fnMicrom}\fnMicrom} {\fnMicrom}\fnMicrosoft}\fnMicrosoft}\fnMicrosoft}\f}\fnMinMicrosoft}\fnMientras,\fnMinMinMinun}\fnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMin$

Las ecuaciones relacionan las propiedades de una capa de fluido bidimensional calentada uniformemente desde abajo y enfriada desde arriba. En particular, las ecuaciones describen la tasa de cambio de tres cantidades con respecto al tiempo: x es proporcional a la tasa de convección, y a la variación de temperatura horizontal y z a la variación de temperatura vertical. Las constantes σ, ρ y β son parámetros del sistema proporcionales al número de Prandtl, al número de Rayleigh y a ciertas dimensiones físicas de la propia capa.

Las ecuaciones de Lorenz pueden surgir en modelos simplificados para láseres, dinamos, termosifones, motores de corriente continua sin escobillas, circuitos eléctricos, reacciones químicas y ósmosis directa. Las ecuaciones de Lorenz también son las ecuaciones que rigen en el espacio de Fourier la rueda hidráulica de Malkus. La rueda hidráulica de Malkus exhibe un movimiento caótico en el que, en lugar de girar en una dirección a una velocidad constante, su rotación se acelerará, se ralentizará, se detendrá, cambiará de dirección y oscilará de un lado a otro entre combinaciones de tales comportamientos de manera impredecible.

Desde un punto de vista técnico, el sistema de Lorenz es no lineal, aperiódico, tridimensional y determinista. Las ecuaciones de Lorenz han sido objeto de cientos de artículos de investigación y de al menos un estudio extenso.

Normalmente se supone que los parámetros σ, ρ y β son positivos. Lorenz utilizó los valores σ = 10, β = ⁠8/3⁠ y ρ = 28. El sistema muestra un comportamiento caótico para estos valores (y otros cercanos).

Si ρ < 1 entonces solo hay un punto de equilibrio, que está en el origen. Este punto corresponde a la ausencia de convección. Todas las órbitas convergen al origen, que es un atractor global, cuando ρ < 1.

Una bifurcación de horquilla ocurre en *** = 1, y *** ■ 1 dos puntos críticos adicionales aparecen en $${\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\beta {\rho -1)}}\rho -1\right)\quad {\text{y}\quad\left(-{\sqrt {\beta (\rho -1)},-{\sqh}\f} {\f}\f}\f}}\f}\f}\f}\f}\f}\f}\f}\f}\f}\f}\p]}\f}\f}\fnun}\p]}\fnMinMinMinMinun}\fnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMientras no es mientras no es mientras no es mientras no es mientras no es mientras no me gusta, no me gusta. }$$ Estos corresponden a la convección constante. Este par de puntos de equilibrio es estable sólo si

${\sigma +\beta +3}{\sigma -\beta -1}}}$

lo cual sólo puede cumplirse para valores positivos de ρ si σ > β + 1. En el valor crítico, ambos puntos de equilibrio pierden estabilidad a través de una bifurcación de Hopf subcrítica.

Cuando ρ = 28, σ = 10 y β = ⁠8/3⁠, el sistema de Lorenz tiene soluciones caóticas (pero no todas las soluciones son caóticas). Casi todos los puntos iniciales tenderán a un conjunto invariante –el atractor de Lorenz–, un atractor extraño, un fractal y un atractor autoexcitado con respecto a los tres equilibrios. Su dimensión de Hausdorff se estima a partir de la dimensión de Lyapunov (dimensión de Kaplan-Yorke) como 2,06±0,01, y la dimensión de correlación se estima como 2,05±0,01. La fórmula exacta de la dimensión de Lyapunov del atractor global se puede encontrar analíticamente bajo restricciones clásicas sobre los parámetros:

${\displaystyle 3-{\frac {2(\sigma +\beta +1)}{\sigma +1+{\sqrt {\left(\sigma -1\right)^{2}+4\sigma \rho }$

El atractor de Lorenz es difícil de analizar, pero la acción de la ecuación diferencial sobre el atractor se describe mediante un modelo geométrico bastante simple. La demostración de que esto es así es el decimocuarto problema de la lista de problemas de Smale. Este problema fue el primero en ser resuelto por Warwick Tucker en 2002.

Para otros valores de ρ, el sistema muestra órbitas periódicas anudadas. Por ejemplo, con ρ = 99,96 se convierte en un nudo toroidal T(3,2).

Soluciones de ejemplo del sistema Lorenz para diferentes valores de ***
*** = 14, σ = 10, β = ⁠8/3⁠ (Agrandar)	*** = 13, σ = 10, β = ⁠8/3⁠ (Agrandar)
*** = 15, σ = 10, β = ⁠8/3⁠ (Agrandar)	*** = 28, σ = 10, β = ⁠8/3⁠ (Agrandar)
Para valores pequeños de ***, el sistema es estable y evoluciona a uno de los dos puntos de atracción fijo. Cuando *** √≥ 24.74, los puntos fijos se vuelven repulsores y la trayectoria es repelida por ellos de una manera muy compleja.

La dependencia sensible de la condición inicial
Hora t = 1 (Agrandar)	Hora t = 2 (Agrandar)	Hora t = 3 (Agrandar)
Estas cifras se hacen utilizando *** = 28, σ = 10 y β = ⁠8/3⁠ — mostrar tres segmentos de tiempo de la evolución 3-D de dos trayectorias (una en azul, la otra en amarillo) en el atraedor Lorenz comenzando en dos puntos iniciales que difieren sólo por 10; 5 - en el x- coordinado. Inicialmente, las dos trayectorias parecen coincidir (sólo el amarillo se puede ver, como se dibuja sobre el azul) pero, después de algún tiempo, la divergencia es obvia.

Divergencia de trayectorias cercanas.
Evolución de tres trayectorias inicialmente cercanas del sistema Lorenz. En esta animación la ecuación está integrada numéricamente usando una rutina Runge-Kutta, hecha a partir de tres condiciones iniciales (0.9,0,0) (verde) (1.0,0,0) (azul) y (1,0,0) (red). Producido con WxMaxima.
Los parámetros son: ${\displaystyle \rho =28}$, ${\displaystyle \sigma =10}$ y ${\displaystyle \beta =8/3}$. La divergencia Siginificante se ve alrededor ${\displaystyle t=24.0}$, más allá de lo cual las trayectorias se vuelven incorrelacionadas. El gráfico de tamaño completo se puede acceder aquí.

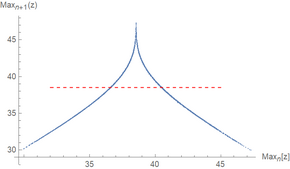
En la Figura 4 de su artículo, Lorenz trazó un gráfico del valor máximo relativo en la dirección z alcanzado por el sistema contra el máximo relativo anterior en la dirección z. Este procedimiento se conoció posteriormente como mapa de Lorenz (que no debe confundirse con un gráfico de Poincaré, que traza las intersecciones de una trayectoria con una superficie prescrita). El gráfico resultante tiene una forma muy similar al mapa de tienda de campaña. Lorenz también descubrió que cuando el valor máximo de z está por encima de un cierto límite, el sistema cambiará al siguiente lóbulo. Combinando esto con el caos que se sabe que exhibe el mapa de tienda de campaña, demostró que el sistema cambia entre los dos lóbulos de manera caótica.

En los últimos años, una serie de artículos sobre modelos Lorenz de alta dimensión han dado lugar a un modelo Lorenz generalizado, que puede simplificarse en el modelo clásico Lorenz para tres variables estatales o el siguiente modelo Lorenz de cinco dimensiones para cinco variables estatales: $${\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft} {\fnMicrosoft}} {\f}\f} {\f} {\f}\f}\f}\f}\f}\f} {\f}\fnMicrom}\f}\f} {\fnMicrom}\f}\f}\fnK\f}\f}\f}\f}\f}\f}\f}\fnK\f} {\fnMinMissc\f}\fnK\f}\fnK\f}\fnMis}\fnMicrosoft}\fnK\f}\fnK\f}\fnK\f}\fnK\ t} {=2xy_{1}-4\beta z_{1}\end{aligned}}$$

Una elección del parámetro ${\fnMicrosoftstyle D_{0}={\dfrac {}{3}}}$ se ha aplicado para ser coherente con la elección de los otros parámetros. Ver detalles.

utilizando Parcelas# define el atractivo Lorenz@kwdef mutable struct Lorenz ♪::Float64 = 0,02 σ::Float64 = 10 ***::Float64 = 28 β::Float64 = 8/3 x::Float64 = 2 Sí.::Float64 = 1 z::Float64 = 1finalfunción ¡Paso!()l::Lorenz) dx = l.σ * ()l.Sí. - l.x); l.x += l.♪ * dx dy = l.x * ()l.*** - l.z) - l.Sí.; l.Sí. += l.♪ * dy dz = l.x * l.Sí. - l.β * l.z; l.z += l.♪ * dzfinaltractor = Lorenz()# inicializar un complot 3D con 1 serie vacíaplt = plot3d() 1, xlim = ()-30, 30), Ylim = ()-30, 30), zlim = ()0, 60), Título = "Lorenz Attractor", marcador = 2,)# Construir un gif animado empujando nuevos puntos a la trama, ahorrando cada décimo marco@gif para i=1:1500 ¡Paso!()tractor) ¡Empujen!()plt, tractor.x, tractor.Sí., tractor.z)final cada uno 10

deq := [diff()x()t), t) = 10*()Sí.()t) - x()t), diff()Sí.()t), t) = 28*x()t) - Sí.()t) - x()t)*z()t), diff()z()t), t) = x()t)*Sí.()t) - 8/3*z()t):con()DEtools):DEplot3d()deq, {}x()t), Sí.()t), z()t), t = 0 .. 100, [[2]x()0) = 10, Sí.()0) = 10, z()0) = 10]], adopción de medidas = 0,01, x = -20 .. 20, Sí. = -25 .. 25, z = 0 .. 50, linecolour = pecado()t*Pi/3), espesor = 1, orientación = [-40, 80], Título = `Lorenz Chaotic Attractor `);

[sigma, rho, beta]: [10, 28, 8/3]$eq: [sigma*()Sí.-x), x*()rho-z)-Sí., x*Sí.-beta*z]$Sol: rk()eq, [x, Sí., z] [1, 0, 0] [t, 0, 50, 1/100])Len: longitud()Sol)$x: lista()Sol[k[ ]2] k, Len)$Sí.: lista()Sol[k[ ]3] k, Len)$z: lista()Sol[k[ ]4] k, Len)$dibujo3d()points_joined=verdadero, point_type=1, puntos()x, Sí., z), proporcional_axes=xyz)$

% Resolver a intervalos de tiempo [0,100] con condiciones iniciales [1,1]% ''f'' es conjunto de ecuaciones diferenciales% ''a' es matriz que contiene variables x, y% 't' es variable tiemposigma = 10;beta = 8/3;rho = 28;f = @(t,a) [-sigma*a()1) + sigma*a()2); rho*a()1) - a()2) - a()1)*a()3); -beta*a()3) + a()1)*a()2);[t,a] = ode45()f,[0 100], [1 1 1]); % Runge-Kutta 4th/5th order ODE solverparcela3()a(:1),a(:2),a(:3)

Método estándar:

tiende = 50;eq = {}x'[t] == σ ()Sí.[t] - x[t]),  Sí.'[t] == x[t] ()*** - z[t]) - Sí.[t]  z'[t] == x[t] Sí.[t] - β z[t]}init = {}x[0] == 10, Sí.[0] == 10, z[0] == 10};pares = {}σ- No.10, ***- No.28, β- No.8/3};{}xs, Ys, z} =  NDSolveValue[ {}eq /. pares, init} {}x, Sí., z} {}t, 0, tiende}]ParametricPlot3D[ {}xs[t] Ys[t] z[t] {}t, 0, tiende}

Menos verboso:

Lorenz = NonlinearStateSpaceModel[{}σ ()Sí. - x), x ()*** - z) - Sí., x Sí. - β z} {} {}x, Sí., z} {}σ, ***, β}]Soln[#] = StateResponse[ {}Lorenz, {}10, 10, 10} {}10, 28, 8/3} {}t, 0, 50}]ParametricPlot3D[Soln[t] {}t, 0, 50}

importación matplotlib.pyplot como pltimportación numposo como npdef Lorenz()xyz, *, s=10, r=28, b=2.667): " Parámetros -------- xyz: tipo array, forma (3,) Punto de interés en el espacio tridimensional. s, r, b: flotador Parámetros que definen el atractor Lorenz. Devoluciones --- xyz_dot: array, shape (3,) Valores de los derivados parciales de Lorenz a *xyz*. " x, Sí., z = xyz x_dot = s*()Sí. - x) Y... = r*x - Sí. - x*z z_dot = x*Sí. - b*z Regreso np.array([2]x_dot, Y..., z_dot])♪ = 0,01num_steps = 10000xyzs = np.vacío(()num_steps + 1, 3) # Necesita uno más para los valores inicialesxyzs[0] = ()0., 1., 1.05) # Establecer valores iniciales# Paso a través del "tiempo", calculando los derivados parciales en el punto actual# y utilizarlos para estimar el siguiente puntopara i dentro rango()num_steps): xyzs[i + 1] = xyzs[i] + Lorenz()xyzs[i]) * ♪# Plotax = plt.gráfico().add_subplot()proyección='3d ')ax.parcela()*xyzs.T, #=0.6)ax.set_xlabel()"X Axis")ax.set_ylabel()"Y Axis")ax.set_zlabel()"Z Axis")ax.set_title()"Lorenz Attractor")plt.show()

biblioteca()deSolve)biblioteca()conspiración)# Parámetrosprm . lista()sigma = 10, rho = 28, beta = 8/3)# valores inicialesvarini . c() X = 1, Y = 1,  Z = 1)Lorenz . función ()t, Vars, prm) {} con()as.list()Vars), {} dX . prm$sigma*()Y - X) d Y . X*()prm$rho - Z) - Y dZ . X*Y - prm$beta*Z Regreso()lista()c()dX, d Y, dZ)) })}veces . seq()desde = 0, a = 100, por = 0,01)# Call ode solverFuera. . ode()Sí. = varini, veces = veces, func = Lorenz, parms = prm)# para asignar color a puntosGfill . función ()rep Arr, largo) {} rep()rep Arr, techo()largo/longitud()rep Arr) [)1:largo]}dout . as.data.frame()Fuera.)dout$color . Gfill()arco iris()10), #()dout)# Producción gráfica con Plotly:plot_ly() datos=dout, x = ~X, Sí. = ~Y, z = ~Z, Tipo = 'scatter3d ', modo = 'líneas ', opacidad = 1, línea = lista()ancho = 6, color = ~color, reverendoscale = FALSE))

Como se muestra en el artículo original de Lorenz, el sistema de Lorenz es una versión reducida de un sistema más grande estudiado anteriormente por Barry Saltzman. Las ecuaciones de Lorenz se derivan de la aproximación de Oberbeck-Boussinesq a las ecuaciones que describen la circulación de fluidos en una capa superficial de fluido, calentada uniformemente desde abajo y enfriada uniformemente desde arriba. Esta circulación de fluidos se conoce como convección de Rayleigh-Bénard. Se supone que el fluido circula en dos dimensiones (vertical y horizontal) con condiciones de contorno rectangulares periódicas.

Las ecuaciones diferenciales parciales que modelan la función de corriente y la temperatura del sistema se someten a una aproximación espectral de Galerkin: los campos hidrodinámicos se expanden en series de Fourier, que luego se truncan severamente a un solo término para la función de corriente y dos términos para la temperatura. Esto reduce las ecuaciones del modelo a un conjunto de tres ecuaciones diferenciales ordinarias no lineales acopladas. Se puede encontrar una derivación detallada, por ejemplo, en textos de dinámica no lineal de Hilborn (2000), Apéndice C; Bergé, Pomeau y Vidal (1984), Apéndice D; o Shen (2016), Materiales complementarios.

La comunidad científica acepta que las características caóticas encontradas en los modelos de Lorenz de baja dimensión podrían representar características de la atmósfera de la Tierra (), lo que da lugar a la afirmación de que “el clima es caótico”. En comparación, basándose en el concepto de coexistencia de atractores dentro del modelo generalizado de Lorenz y el modelo original de Lorenz (), Shen y sus coautores propusieron una visión revisada de que “el clima posee tanto caos como orden con una predictibilidad distintiva”. La visión revisada, que es una ampliación de la visión convencional, se utiliza para sugerir que “las características caóticas y regulares encontradas en los modelos teóricos de Lorenz podrían representar mejor las características de la atmósfera de la Tierra”.

El 14o problema de Smale dice: '¿Las propiedades de la atracción Lorenz exhiben aquello de un extraño atracción?'. El problema fue respondido afirmativamente por Warwick Tucker en 2002. Para probar este resultado, Tucker utilizó métodos numéricos rigurosos como formas aritméticas y normales de intervalo. Primero, Tucker definió una sección transversal ${\displaystyle \Sigma \subset \{x_{3}=r-1\}$ que se corta transversalmente por las trayectorias de flujo. De este modo, se puede definir el mapa de primera vuelta ${\displaystyle P}$, que asigna a cada uno ${\displaystyle x\in \Sigma }$ el punto ${\displaystyle P(x)}$ donde la trayectoria de ${\displaystyle x}$ primer intersectos ${\displaystyle \Sigma$.

Entonces la prueba se divide en tres puntos principales que se prueban e implican la existencia de un atractor extraño. Los tres puntos son:

• Existe una región ${\displaystyle N\subset \Sigma }$ invariante bajo el mapa de primera vuelta, lo que significa ${\displaystyle P(N)\subset N}$.
• El mapa de retorno admite un campo de cono invariable.
• Los vectores dentro de este campo de cono invariante se expanden uniformemente por el derivado ${\displaystyle DP}$ del mapa de retorno.

Para probar el primer punto, notamos que la sección transversal ${\displaystyle \Sigma$ es cortado por dos arcos formados por ${\displaystyle P(\Sigma)}$. Tucker cubre la ubicación de estos dos arcos por pequeños rectángulos ${\displaystyle R_{i}$, la unión de estos rectángulos da ${\displaystyle N}$. Ahora, el objetivo es probar que para todos los puntos en ${\displaystyle N}$, el flujo traerá de vuelta los puntos en ${\displaystyle \Sigma$, dentro ${\displaystyle N}$. Para hacer eso, tomamos un plan ${\displaystyle \Sigma}$ infra ${\displaystyle \Sigma$ a distancia ${\displaystyle h}$ pequeño, luego tomando el centro ${\displaystyle C_{i}$ de ${\displaystyle R_{i}$ y utilizando el método de integración Euler, se puede estimar dónde traerá el flujo ${\displaystyle C_{i}$ dentro ${\displaystyle \Sigma}$ que nos da un nuevo punto ${\displaystyle c_{i}}$. Entonces, se puede estimar dónde están los puntos ${\displaystyle \Sigma$ será mapeado en ${\displaystyle \Sigma}$ usando la expansión de Taylor, esto nos da un nuevo rectángulo ${\displaystyle R_{i}$ centrado en ${\displaystyle C_{i}$. Así sabemos que todos los puntos ${\displaystyle R_{i}$ será mapeado en ${\displaystyle R_{i}$. El objetivo es hacer este método recursivamente hasta que el flujo regrese a ${\displaystyle \Sigma$ y obtenemos un rectángulo ${\displaystyle Rf_{i}$ dentro ${\displaystyle \Sigma$ tal que sabemos que ${\displaystyle P(R_{i})\subset Rf_{i}$. El problema es que nuestra estimación puede llegar a ser imprecisa después de varias iteraciones, así lo que hace Tucker es dividir ${\displaystyle R_{i}$ en rectángulos más pequeños ${\displaystyle R_{i,j}$ y luego aplicar el proceso recursivamente. Otro problema es que al aplicar este algoritmo, el flujo se vuelve más 'horizontal', lo que conduce a un aumento dramático de la imprecisión. Para evitarlo, el algoritmo cambia la orientación de las secciones transversales, convirtiéndose en horizontal o vertical.

• 
  Una solución en el atractivo Lorenz trazado en alta resolución en el xz avión.
• 
  Una solución en el atacante Lorenz que se convirtió en SVG.
• Una animación que muestra trayectorias de múltiples soluciones en un sistema Lorenz.
• 
  Una solución en el atraedor Lorenz que se ha convertido en un alambre de metal para mostrar dirección y estructura 3D.
• Una animación que muestra la divergencia de soluciones cercanas al sistema Lorenz.
• 
  Una visualización del atractivo Lorenz cerca de un ciclo intermitente.
• 
  Dos aerodinámicas en un sistema Lorenz, desde *** = 0 a *** = 28 ()σ = 10, β = ⁠8/3⁠).
• 
  Animación de un sistema Lorenz con dependencia rho.
• 
  Animación del atractivo Lorenz en la caja de herramientas de la dinámica del cerebro.

• Conjetura de Edén en la dimensión de Lyapunov
• Modelo Lorenz 96
• Lista de mapas caóticos
• Teorema de Taken

• Bergé, Pierre; Pomeau, Yves; Vidal, Christian (1984). Orden dentro de Caos: Hacia un enfoque definiinista de la Turbulencia. Nueva York: John Wiley & Sons. ISBN 978-0-471-84967-4.
• Cuomo, Kevin M.; Oppenheim, Alan V. (1993). "Aplicación precisa del caos sincronizado con aplicaciones a las comunicaciones". Cartas de revisión física. 71 (1): 65–68. Código:1993PhRvL..71...65C. doi:10.1103/PhysRevLett.71.65. ISSN 0031-9007. PMID 10054374.
• Gorman, M.; Widmann, P.J.; Robbins, K.A. (1986). "Dinamismos no lineales de un bucle de convección: Comparación cuantitativa del experimento con la teoría". Fisica D. 19 (2): 255–267. Bibcode:1986PhyD...19..255G. doi:10.1016/0167-2789(86)90022-9.
• Grassberger, P.; Procaccia, I. (1983). "Measuring the strangeness of strange attractors". Fisica D. 9 (1–2): 189–208. Bibcode:1983PhyD....9..189G. doi:10.1016/0167-2789(83)90298-1.
• Haken, H. (1975). "Analogía entre inestabilidades superiores en fluidos y láseres". Cartas Físicas A. 53 (1): 77–78. Bibcode:1975PhLA...53...77H. doi:10.1016/0375-9601(75)90353-9.
• Hemati, N. (1994). "Atractores extraños en motores DC sin cepillos". Transacciones IEEE en circuitos y sistemas I: Teoría fundamental y aplicaciones. 41 (1): 40–45. doi:10.1109/81.260218. ISSN 1057-7122.
• Hilborn, Robert C. (2000). Dinámica de Caos y Nolinear: Introducción para Científicos e Ingenieros (segunda edición). Oxford University Press. ISBN 978-0-19-850723-9.
• Hirsch, Morris W.; Smale, Stephen; Devaney, Robert (2003). Ecuaciones diferenciales, sistemas dinámicos, " Introducción al caos (Segunda edición). Boston, MA: Prensa Académica. ISBN 978-0-12-349703-1.
• Knobloch, Edgar (1981). "Chaos en la dinamo de disco segmentado". Cartas Físicas A. 82 (9): 439-440. Bibcode:1981PhLA...82..439K doi:10.1016/0375-9601(81)90274-7.
• Kolář, Miroslav; Gumbs, Godfrey (1992). "Teoría para la observación experimental del caos en una rueda giratoria de agua". Examen físico A. 45 (2): 626-637. Código:1992PhRvA..45..626K. doi:10.1103/PhysRevA.45.626. PMID 9907027.
• Leonov, G.A.; Kuznetsov, N.V.; Korzhemanova, N.A.; Kusakin, D.V. (2016). "Fórmula de dimensión de Lyapunov para el atraccióndor global del sistema Lorenz". Comunicaciones en ciencias no lineales y simulación numérica. 41: 84-103. arXiv:1508.07498. Bibcode:2016CNSNS..41...84L. doi:10.1016/j.cnsns.2016.04.032. S2CID 119614076.
• Lorenz, Edward Norton (1963). " Flujo no perpeúdico definitivo". Journal of the Atmospheric Sciences. 20 (2): 130–141. Bibcode:1963JAtS...20..130L. doi:10.1175/1520-0469(1963)020 100130:DNF confía2.0.CO;2.
• Mishra, Aashwin; Sanghi, Sanjeev (2006). "Un estudio de la rueda asimétrica de Malkus: Las ecuaciones de Lorenz sesgadas". Caos: Revista Interdisciplinaria de Ciencias Nolineales. 16 (1): 013114. Bibcode:2006Chaos..16a3114M. doi:10.1063/1.2154792. PMID 16599745.
• Pchelintsev, A.N. (2014). "Modelación numérica y física de la dinámica del sistema Lorenz". Análisis numérico y aplicaciones. 7 (2): 159–167. doi:10.1134/S1995423914020098. S2CID 123023929.
• Polonia, Douglas (1993). "Catálisis cooperativa y caos químico: un modelo químico para las ecuaciones de Lorenz". Fisica D. 65 (1): 86–99. Código:1993...65...86P. doi:10.1016/0167-2789(93)90006-M.
• Saltzman, Barry (1962). "Finite Amplitude Free Convection como un problema de valor inicial—I". Journal of the Atmospheric Sciences. 19 (4): 329-341. Bibcode:1962JAtS...19..329S. doi:10.1175/1520-0469(1962)019 100329:FAFCAA confía2.0.CO;2.
• Shen, B.-W. (2015-12-21). "Retroalimentación no lineal en un modelo Lorenz de seis dimensiones: impacto de un término de calefacción adicional". Procesos no lineales en Geofísica. 22 (6): 749–764. doi:10.5194/npg-22-749-2015. ISSN 1607-7946.
• Sparrow, Colin (1982). Ecuaciones Lorenz: Bifurcaciones, Caos y Extraños Attractores. Springer.
• Tucker, Warwick (2002). "Un resolver de ODE riguroso y el 14o problema de Smale" (PDF). Fundaciones de Matemáticas Computacionales. 2 (1): 53-117. CiteSeerX 10.1.1.545.3996. doi:10.1007/s002080010018. S2CID 353254.
• Tzenov, Stephan (2014). "Atractores extraños caracterizando la inestabilidad osmótica". arXiv:1406.0979v1 [physics.flu-dyn].
• Viana, Marcelo (2000). "¿Qué hay de nuevo en Lorenz extraños atractivos?". The Mathematical Intelligencer. 22 (3): 6–19. doi:10.1007/BF03025276. S2CID 121427433.
• Lorenz, Edward N. (1960). "La predicción estadística de soluciones de ecuaciones dinámicas" (PDF). Simposium on Numerical Weather Prediction in Tokyo. Archivado desde el original (PDF) on 2019-05-23. Retrieved 2020-09-16.

• G.A. Leonov " N.V. Kuznetsov (2015). "Sobre diferencias y similitudes en el análisis de sistemas Lorenz, Chen y Lu". Matemáticas aplicadas y computación. 256: 334-343. arXiv:1409.8649. doi:10.1016/j.amc.2014.12.132.
• Pchelintsev, A.N. (2022). "En un método de alta precisión para estudiar atractores de sistemas dinámicos y sistemas de tipo explosivo". Matemáticas. 10 (8): 1207. arXiv:2206.08195. doi:10.3390/math10081207.

• "Lorenz attractor", Enciclopedia de Matemáticas, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Lorenz attractor". MathWorld.
• Lorenz de atracción por Rob Morris, Wolfram Demonstrations Project.
• Ecuación de Lorenz Archivado 2009-06-07 en la Máquina Wayback en planetmath.org
• Caos sincronizados y comunicaciones privadas, con Kevin Cuomo. La implementación de Lorenz en un circuito electrónico.
• Animación interactiva de Lorenz (necesita el plugin de Adobe Shockwave)
• 3D Attractores: programa Mac para visualizar y explorar el atractivo Lorenz en 3 dimensiones
• Lorenz Attractor implementado en electrónica analógica
• Animación interactiva Lorenz Attractor (implementada en Ada con GTK+. Fuentes ejecutables
• Interactive web based Lorenz Attractor made with Iodide