Sistema de ecuaciones lineales

En matemáticas, un sistema de ecuaciones lineales (o sistema lineal) es una colección de una o más ecuaciones lineales que involucran las mismas variables.

Un sistema lineal en tres variables determina una colección de planos El punto de intersección es la solución.

Por ejemplo,

${displaystyle {begin{cases}3x+2y-z=12x-2y+4z=-2\\-x+{ {1}{2}y-z=0end{cases}}$

es un sistema de tres ecuaciones en las tres variables x, y, z. Una solución a un sistema lineal es una asignación de valores a las variables tal que todas las ecuaciones se satisfagan simultáneamente. Una solución al sistema anterior viene dada por el triple ordenado

${displaystyle (x,y,z)=(1,-2,-2),}$

ya que hace que las tres ecuaciones sean válidas. La palabra "sistema" indica que las ecuaciones deben considerarse colectivamente, en lugar de individualmente.

En matemáticas, la teoría de los sistemas lineales es la base y parte fundamental del álgebra lineal, materia que se utiliza en la mayor parte de las matemáticas modernas. Los algoritmos computacionales para encontrar las soluciones son una parte importante del álgebra lineal numérica y juegan un papel destacado en la ingeniería, la física, la química, la informática y la economía. Un sistema de ecuaciones no lineales a menudo se puede aproximar mediante un sistema lineal (ver linealización), una técnica útil al hacer un modelo matemático o una simulación por computadora de un sistema relativamente complejo.

Muy a menudo, los coeficientes de las ecuaciones son números reales o complejos y las soluciones se buscan en el mismo conjunto de números, pero la teoría y los algoritmos aplican para coeficientes y soluciones en cualquier campo. Para soluciones en un dominio integral como el anillo de los enteros, o en otras estructuras algebraicas, se han desarrollado otras teorías, consulte Ecuación lineal sobre un anillo. La programación lineal entera es una colección de métodos para encontrar el "mejor" solución entera (cuando hay muchas). La teoría de la base de Gröbner proporciona algoritmos cuando los coeficientes y las incógnitas son polinomios. También la geometría tropical es un ejemplo de álgebra lineal en una estructura más exótica.

Ejemplos elementales

Ejemplo trivial

El sistema de una ecuación en una incógnita

${displaystyle 2x=4}$

tiene la solución

${displaystyle x=2.}$

Sin embargo, se suele considerar que un sistema lineal tiene al menos dos ecuaciones.

Ejemplo simple no trivial

El tipo más simple de sistema lineal no trivial implica dos ecuaciones y dos variables:

${displaystyle {begin{alignedat}{5}2x limitándose;+; limitada3y reducida;=; limitada6 limitada\4x limitada;+; limitada9y reducida;=; limitante {cHFF}}}}}}$

Un método para resolver ese sistema es el siguiente. Primero, resolver la ecuación superior para ${displaystyle x}$ en términos de ${displaystyle y}$:

${displaystyle x=3-{frac Sí.$

Ahora sustituya esta expresión por x en la ecuación inferior:

${displaystyle 4left(3-{2}yright)+9y=15.}$

Esto resulta en una sola ecuación que implica solamente la variable ${displaystyle y}$. La solución da ${displaystyle y=1}$, y sustituir esto de nuevo en la ecuación para ${displaystyle x}$ rendimientos ${displaystyle x={frac {3}{2}}$. Este método generaliza los sistemas con variables adicionales (ver "elimination of variables" abajo, o el artículo sobre álgebra elemental).

Forma general

Un sistema general de m ecuaciones lineales con n incógnitas y coeficientes se puede escribir como

${displaystyle {begin{cases}a_{11}x_{1}+a_{12}x_{2}+dots +a_{1n}x_{n}+b_{1}=0a_{21}x_{1}+a_{22}x_{2}+dots +a_{2n}x_{n}+b_{2}=0\\vdots \a_{m1}x_{1}+a_{m2}x_{2}+dots - ¿Qué?$

Donde ${displaystyle x_{1},x_{2},dotsx_{n}$ son los desconocidos, ${displaystyle a_{11},a_{12},dotsa_{mn}$ son los coeficientes del sistema, y ${displaystyle B_{1},b_{2},dotsb_{m}$ son los términos constantes.

A menudo, los coeficientes y las incógnitas son números reales o complejos, pero también se ven números enteros y racionales, así como polinomios y elementos de una estructura algebraica abstracta.

Ecuación vectorial

Una vista extremadamente útil es que cada incógnita es un peso para un vector de columna en una combinación lineal.

${displaystyle x_{1}{begin{bmatrix}a_{11}a_{21}\\vdots \a_{m1}end{bmatrix}+x_{2}{begin{bmatrix}a_{12}a_{22}\\vdots \a_{m2}end{bmatrix}dots ##x_{n}{bmatrix}a_{1n}a_{2n}\\vdots \a_{mn}end{bmatrix}+{begin{bmatrix}b_{1}b_{2}\\vdots {fnK}=0}$

Esto permite que todo el lenguaje y la teoría de los espacios vectoriales (o más generalmente, módulos) se apliquen. Por ejemplo, la colección de todas las combinaciones lineales posibles de los vectores en el lado izquierdo se llama su span, y las ecuaciones tienen una solución justo cuando el vector de la derecha está dentro de ese lapso. Si cada vector dentro de ese lapso tiene exactamente una expresión como combinación lineal de los vectores de la izquierda dados, entonces cualquier solución es única. En cualquier caso, el lapso tiene una base de vectores linealmente independientes que garantizan exactamente una expresión; y el número de vectores en esa base (su dimensión) no puede ser mayor que m o n, pero puede ser menor. Esto es importante porque si tenemos m vectores independientes, se garantiza una solución independientemente del lado derecho y, de lo contrario, no se garantiza.

Ecuación matricial

La ecuación vectorial es equivalente a una ecuación matricial de la forma

${displaystyle Amathbf {x} =mathbf {b}$

donde A es una matriz m×n, x es un vector columna con n entradas, y b es un vector de columna con m entradas.

${displaystyle A={begin{bmatrix}a_{11} limita_{12} "A_{1n}a_{21} 'a_{2n}\vdots > 'vdots > {mn}end{bmatrix}},quad mathbf {x} ={begin{bmatrix}x_{1}x_{2}vdots \x_{n}end{bmatrix}},quad mathbf {b} ={begin{bmatrix}b_{1}b_{2}\\vdots {fnK}}$

El número de vectores en una base para el lapso ahora se expresa como el rango de la matriz.

Conjunto de soluciones

La solución para las ecuaciones x − Sí. = 1 - y 3x + Sí. = 9 es el único punto (2, 3).

Una solución de un sistema lineal es una asignación de valores a las variables x₁, < i>x₂,..., x_n tales que cada una de las ecuaciones se satisface. El conjunto de todas las soluciones posibles se denomina conjunto de soluciones.

Un sistema lineal puede comportarse de cualquiera de las tres formas posibles:

1. El sistema tiene infinitamente muchas soluciones.
2. El sistema tiene un solo solución única.
3. El sistema tiene sin solución.

Interpretación geométrica

Para un sistema que involucra dos variables (x e y), cada ecuación lineal determina una línea en el plano xy. Debido a que una solución a un sistema lineal debe satisfacer todas las ecuaciones, el conjunto solución es la intersección de estas líneas y, por lo tanto, es una línea, un solo punto o el conjunto vacío.

Para tres variables, cada ecuación lineal determina un plano en el espacio tridimensional y el conjunto de soluciones es la intersección de estos planos. Así, el conjunto solución puede ser un plano, una línea, un solo punto o el conjunto vacío. Por ejemplo, como tres planos paralelos no tienen un punto común, el conjunto solución de sus ecuaciones está vacío; el conjunto solución de las ecuaciones de tres planos que se cortan en un punto es un solo punto; si tres planos pasan por dos puntos, sus ecuaciones tienen al menos dos soluciones comunes; de hecho, el conjunto solución es infinito y consiste en toda la línea que pasa por estos puntos.

Para n variables, cada ecuación lineal determina un hiperplano en un espacio n-dimensional. El conjunto solución es la intersección de estos hiperplanos, y es un plano, que puede tener cualquier dimensión inferior a n.

Comportamiento general

La solución establecida para dos ecuaciones en tres variables es, en general, una línea.

En general, el comportamiento de un sistema lineal está determinado por la relación entre el número de ecuaciones y el número de incógnitas. Aquí, "en general" significa que un comportamiento diferente puede ocurrir para valores específicos de los coeficientes de las ecuaciones.

• En general, un sistema con menos ecuaciones que desconocidos tiene infinitamente muchas soluciones, pero puede no tener ninguna solución. Este sistema se conoce como un sistema subdeterminado.
• En general, un sistema con el mismo número de ecuaciones y desconocidos tiene una única solución.
• En general, un sistema con más ecuaciones que desconocidos no tiene solución. Este sistema también se conoce como un sistema sobredeterminado.

En el primer caso, la dimensión del conjunto solución es, en general, igual a n − m, donde n es el número de variables y m es el número de ecuaciones.

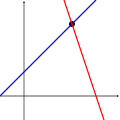
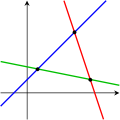
Las siguientes imágenes ilustran esta tricotomía en el caso de dos variables:

Una ecuación	Dos ecuaciones	Tres ecuaciones

El primer sistema tiene infinitas soluciones, es decir, todos los puntos de la línea azul. El segundo sistema tiene una única solución única, a saber, la intersección de las dos líneas. El tercer sistema no tiene soluciones, ya que las tres líneas no comparten un punto común.

Debe tenerse en cuenta que las imágenes de arriba muestran solo el caso más común (el caso general). Es posible que un sistema de dos ecuaciones y dos incógnitas no tenga solución (si las dos líneas son paralelas), o que un sistema de tres ecuaciones y dos incógnitas sea solucionable (si las tres líneas se cruzan en un solo punto).

Un sistema de ecuaciones lineales se comporta de manera diferente al caso general si las ecuaciones son linealmente dependientes, o si es inconsistente y no tiene más ecuaciones que incógnitas.

Propiedades

Independencia

Las ecuaciones de un sistema lineal son independientes si ninguna de las ecuaciones se puede derivar algebraicamente de las demás. Cuando las ecuaciones son independientes, cada ecuación contiene nueva información sobre las variables, y eliminar cualquiera de las ecuaciones aumenta el tamaño del conjunto de soluciones. Para ecuaciones lineales, la independencia lógica es lo mismo que la independencia lineal.

Las ecuaciones x − 2Sí. = 1 -, 3x + 5Sí. = 8, y 4x + 3Sí. = 7 dependen linealmente.

Por ejemplo, las ecuaciones

${displaystyle 3x+2y=6;;;;{y};;;;;6x+4y=12}$

no son independientes: son la misma ecuación cuando se escalan por un factor de dos, y producirían gráficos idénticos. Este es un ejemplo de equivalencia en un sistema de ecuaciones lineales.

Para un ejemplo más complicado, las ecuaciones

${displaystyle {begin{alignedat}{5}x limitada;-; limitada2y reducida;=; limitada-1 implica\3x recíprocamente\;+; implicancia5y recíproca;=; < > > > >;.$

no son independientes, porque la tercera ecuación es la suma de las otras dos. De hecho, cualquiera de estas ecuaciones se puede derivar de las otras dos, y cualquiera de las ecuaciones se puede eliminar sin afectar el conjunto de soluciones. Las gráficas de estas ecuaciones son tres rectas que se cortan en un solo punto.

Coherencia

Las ecuaciones 3x + 2Sí. = 6 y 3x + 2Sí. = 12 son inconsistentes.

Un sistema lineal es inconsistente si no tiene solución, en caso contrario se dice que es consistente. Cuando el sistema es inconsistente, es posible derivar una contradicción de las ecuaciones, que siempre se puede reescribir como la afirmación 0 = 1.

Por ejemplo, las ecuaciones

${displaystyle 3x+2y=6;;;;{y};;;;;3x+2y=12}$

son inconsistentes. De hecho, restando la primera ecuación de la segunda y multiplicando ambos lados del resultado por 1/6, obtenemos 0 = 1. Las gráficas de estas ecuaciones en el plano xy son un par de líneas paralelas.

Es posible que tres ecuaciones lineales sean inconsistentes, aunque dos de ellas sean consistentes juntos. Por ejemplo, las ecuaciones

${displaystyle {begin{alignedat}{7}x tendrían problemas;+; tendrían una relación igual;=; limitada1 tendrían una relación2x implican;+; estarían viviendo un punto muerto;=; restanten]$

son inconsistentes. Sumar las dos primeras ecuaciones da 3x + 2y = 2, que se puede restar de la tercera ecuación para rendimiento 0 = 1. Cualquiera de estas dos ecuaciones tiene una solución común. El mismo fenómeno puede ocurrir para cualquier número de ecuaciones.

En general, se producen incoherencias si los lados izquierdos de las ecuaciones de un sistema son linealmente dependientes y los términos constantes no satisfacen la relación de dependencia. Un sistema de ecuaciones cuyos lados izquierdos son linealmente independientes siempre es consistente.

Dicho de otro modo, según el teorema de Rouché-Capelli, cualquier sistema de ecuaciones (sobredeterminado o no) es inconsistente si el rango de la matriz aumentada es mayor que el rango de la matriz de coeficientes. Si, por el contrario, los rangos de estas dos matrices son iguales, el sistema debe tener al menos una solución. La solución es única si y solo si el rango es igual al número de variables. De lo contrario, la solución general tiene k parámetros libres donde k es la diferencia entre el número de variables y el rango; por tanto, en tal caso hay una infinidad de soluciones. El rango de un sistema de ecuaciones (es decir, el rango de la matriz aumentada) nunca puede ser mayor que [el número de variables] + 1, lo que significa que un sistema con cualquier número de ecuaciones siempre puede reducirse a un sistema que tiene un número de ecuaciones independientes que es como máximo igual a [el número de variables] + 1.

Equivalencia

Dos sistemas lineales que utilizan el mismo conjunto de variables son equivalentes si cada una de las ecuaciones del segundo sistema puede derivarse algebraicamente de las ecuaciones del primer sistema y viceversa. Dos sistemas son equivalentes si ambos son inconsistentes o cada ecuación de cada uno de ellos es una combinación lineal de las ecuaciones del otro. De ello se deduce que dos sistemas lineales son equivalentes si y sólo si tienen el mismo conjunto solución.

Resolver un sistema lineal

Existen varios algoritmos para resolver un sistema de ecuaciones lineales.

Describir la solución

Cuando el conjunto de soluciones es finito, se reduce a un solo elemento. En este caso, la solución única es descrita por una secuencia de ecuaciones cuyos lados izquierdos son los nombres de los desconocidos y los lados derecho son los valores correspondientes, por ejemplo, ${displaystyle (x=3,;y=-2,;z=6)}$. Cuando se ha fijado un orden sobre los desconocidos, por ejemplo el orden alfabético, la solución puede describirse como un vector de valores, como ${displaystyle (3,,-2,,6)}$ por el ejemplo anterior.

Para describir un conjunto con un número infinito de soluciones, normalmente algunas de las variables se designan como libres (o independientes, o como parámetros), lo que significa que se les permite tomar cualquier valor, mientras que las variables restantes son dependientes de los valores de las variables libres.

Por ejemplo, considere el siguiente sistema:

${displaystyle {begin{alignedat}{7}x limitada;+; limitándose a tres y tres tardes;-; limitada2z limitándose\;=; curva5 implica3x curva;+; consecutivo5y lentamente;+; positivo 6z consecutivo;=;=; Concluyéntese {alignedat}}}}$

La solución establecida para este sistema se puede describir mediante las siguientes ecuaciones:

${displaystyle x=-7z-1;;;;text{y};;;;y=3z+2{text{}}$

Aquí z es la variable libre, mientras que x e y dependen de z. Cualquier punto en el conjunto de soluciones se puede obtener eligiendo primero un valor para z y luego calculando los valores correspondientes para x e y.

Cada variable libre le da al espacio de la solución un grado de libertad, cuyo número es igual a la dimensión del conjunto de la solución. Por ejemplo, el conjunto de soluciones para la ecuación anterior es una línea, ya que se puede elegir un punto en el conjunto de soluciones especificando el valor del parámetro z. Una solución infinita de orden superior puede describir un plano o un conjunto de dimensiones superiores.

Diferentes opciones para las variables libres pueden conducir a diferentes descripciones del mismo conjunto de soluciones. Por ejemplo, la solución a las ecuaciones anteriores se puede describir alternativamente de la siguiente manera:

${displaystyle y=-{frac {3}{7}}x+{} {11} {7};;;;;{text{and};;;;;;;z={frac} {1}{7}x-{frac {1} {text{}}}} {fnMicrosoft Sans Serif}$

Aquí x es la variable libre, y y y z son dependientes.

Eliminación de variables

El método más simple para resolver un sistema de ecuaciones lineales es eliminar variables repetidamente. Este método se puede describir de la siguiente manera:

1. En la primera ecuación, resolver para una de las variables en términos de las demás.
2. Sustituir esta expresión en las ecuaciones restantes. Esto produce un sistema de ecuaciones con una ecuación menor y desconocida.
3. Repita los pasos 1 y 2 hasta que el sistema se reduzca a una sola ecuación lineal.
4. Resolver esta ecuación y luego volver a sustituir hasta que se encuentre toda la solución.

Por ejemplo, considere el siguiente sistema:

${displaystyle {begin{cases}x+3y-2z=53x+5y+6z=72x+4y+3z=8end{cases}}$

Resolviendo la primera ecuación para x da x = 5 + 2z - 3 y, y reemplazando esto en la segunda y tercera ecuación se obtiene

${displaystyle {begin{cases}y=3z+2y={tfrac {7}{2}z+1end{cases}}$

Dado que la LHS de ambas ecuaciones es igual a y, igualando la RHS de las ecuaciones. Ahora tenemos:

${displaystyle {begin{aligned}3z+2={tfrac {7}{2}z+1\\ Rightarrow z=2end{aligned}$

Sustitución z = 2 en la segunda o tercera ecuación da Sí. = 8, y los valores de Sí. y z en los primeros rendimientos de la ecuación x = −15. Por lo tanto, el conjunto de la solución es el triple ordenado ${displaystyle (x,y,z)=(-15,8,2)}$.

Reducción de filas

En la reducción por filas (también conocida como eliminación gaussiana), el sistema lineal se representa como una matriz aumentada:

${displaystyle left[{begin{array}{rrr habitr}1⁄3 rest3 reducir53 rest5 péndulo6 péndulo72 péndulo3 péndulo8end{array}right]{text{}}}}}}}$

Esta matriz luego se modifica utilizando operaciones de fila elementales hasta que alcanza la forma escalonada de fila reducida. Hay tres tipos de operaciones de fila elementales:

Tipo 1: Cierra las posiciones de dos filas.

Tipo 2: Multiply a row by a nonzero scalar.

Tipo 3: Añadir a una fila un escalar múltiple de otro.

Debido a que estas operaciones son reversibles, la matriz aumentada producida siempre representa un sistema lineal que es equivalente al original.

Existen varios algoritmos específicos para reducir por filas una matriz aumentada, los más simples son la eliminación de Gauss y la eliminación de Gauss-Jordan. El siguiente cálculo muestra la eliminación de Gauss-Jordan aplicada a la matriz anterior:

${$