Sistema de coordenadas Cartesianas

Ilustración de un avión de coordenadas cartesiano. Cuatro puntos están marcados y etiquetados con sus coordenadas: (2, 3) en verde, (3, 1) en rojo, (1,5, 2, 5) en azul, y el origen (0, 0) en púrpura.

Un sistema de coordenadas cartesianas (,) en un plano es un sistema de coordenadas que especifica cada punto de forma única mediante un par de coordenadas numéricas, que son las distancias con signo al punto de dos líneas orientadas perpendiculares fijas, medidas en la misma unidad de longitud. Cada línea de coordenadas de referencia se denomina eje de coordenadas o simplemente eje (plural ejes) del sistema, y el punto donde se encuentran es su origen, en el par ordenado (0, 0). Las coordenadas también se pueden definir como las posiciones de las proyecciones perpendiculares del punto sobre los dos ejes, expresadas como distancias con signo desde el origen.

Uno puede usar el mismo principio para especificar la posición de cualquier punto en el espacio tridimensional por tres coordenadas cartesianas, sus distancias firmadas a tres planos mutuamente perpendiculares (o, de manera equivalente, por su proyección perpendicular sobre tres líneas mutuamente perpendiculares). En general, las coordenadas cartesianas n (un elemento del espacio n real) especifican el punto en un espacio euclidiano n-dimensional para cualquier dimensión n. Estas coordenadas son iguales, hasta el signo, a las distancias del punto a n hiperplanos mutuamente perpendiculares.

Sistema de coordenadas cartesiano con un círculo de radio 2 centrado en el origen marcado en rojo. La ecuación de un círculo es ()x − a)² +Sí. − b)² = r² Donde a y b son las coordenadas del centro ()a, b) y r es el radio.

La invención de las coordenadas cartesianas en el siglo XVII por René Descartes (nombre en latín: Cartesius) revolucionó las matemáticas al proporcionar el primer vínculo sistemático entre la geometría euclidiana y el álgebra. Usando el sistema de coordenadas cartesianas, las formas geométricas (como las curvas) se pueden describir mediante ecuaciones cartesianas: ecuaciones algebraicas que involucran las coordenadas de los puntos que se encuentran en la forma. Por ejemplo, un círculo de radio 2, centrado en el origen del plano, puede describirse como el conjunto de todos los puntos cuyas coordenadas x e y satisfacen la ecuación x² + y² = 4.

Las coordenadas cartesianas son la base de la geometría analítica y proporcionan interpretaciones geométricas esclarecedoras para muchas otras ramas de las matemáticas, como el álgebra lineal, el análisis complejo, la geometría diferencial, el cálculo multivariante, la teoría de grupos y más. Un ejemplo familiar es el concepto de la gráfica de una función. Las coordenadas cartesianas también son herramientas esenciales para la mayoría de las disciplinas aplicadas que se ocupan de la geometría, incluidas la astronomía, la física, la ingeniería y muchas más. Son el sistema de coordenadas más común utilizado en gráficos por computadora, diseño geométrico asistido por computadora y otro procesamiento de datos relacionado con la geometría.

Historia

El adjetivo Cartesiano hace referencia al matemático y filósofo francés René Descartes, quien publicó esta idea en 1637 mientras residía en los Países Bajos. Fue descubierto de forma independiente por Pierre de Fermat, quien también trabajó en tres dimensiones, aunque Fermat no publicó el descubrimiento. La clériga francesa Nicole Oresme utilizó construcciones similares a las coordenadas cartesianas mucho antes de la época de Descartes y Fermat.

Tanto Descartes como Fermat utilizaron un solo eje en sus tratamientos y tienen una longitud variable medida en referencia a este eje. El concepto de usar un par de hachas se introdujo más tarde, después de que Descartes lo hiciera. La Géométrie fue traducida al latín en 1649 por Frans van Schooten y sus alumnos. Estos comentaristas introdujeron varios conceptos al tratar de aclarar las ideas contenidas en el trabajo de Descartes.

El desarrollo del sistema de coordenadas cartesianas jugaría un papel fundamental en el desarrollo del cálculo de Isaac Newton y Gottfried Wilhelm Leibniz. La descripción de dos coordenadas del plano se generalizó más tarde en el concepto de espacios vectoriales.

Desde Descartes se han desarrollado muchos otros sistemas de coordenadas, como las coordenadas polares para el plano y las coordenadas esféricas y cilíndricas para el espacio tridimensional.

Descripción

Una dimensión

Elegir un sistema de coordenadas cartesianas para un espacio unidimensional, es decir, para una línea recta, implica elegir un punto O de la línea (el origen), una unidad de longitud y un orientación para la línea. Una orientación elige cuál de las dos semirrectas determinadas por O es la positiva y cuál la negativa; entonces decimos que la línea "está orientada" (o "puntos") desde la mitad negativa hacia la mitad positiva. Luego, cada punto P de la línea se puede especificar por su distancia desde O, tomada con un signo + o − dependiendo de qué semilínea contiene P.

Una recta con un sistema cartesiano elegido se llama recta numérica. Cada número real tiene una ubicación única en la línea. Por el contrario, cada punto de la línea se puede interpretar como un número en un continuo ordenado, como los números reales.

Dos dimensiones

Un sistema de coordenadas cartesianas en dos dimensiones (también llamado sistema de coordenadas rectangulares o sistema de coordenadas ortogonales) está definido por un par ordenado de líneas perpendiculares (ejes), una sola unidad de longitud para ambos ejes y una orientación para cada eje. El punto donde se encuentran los ejes se toma como origen de ambos, convirtiendo así cada eje en una recta numérica. Para cualquier punto P, se dibuja una línea a través de P perpendicular a cada eje, y la posición donde se encuentra con el eje se interpreta como un número. Los dos números, en ese orden elegido, son las coordenadas cartesianas de P. La construcción inversa permite determinar el punto P dadas sus coordenadas.

La primera y segunda coordenadas se denominan abscisa y ordenada de P, respectivamente; y el punto donde se encuentran los ejes se llama el origen del sistema de coordenadas. Las coordenadas generalmente se escriben como dos números entre paréntesis, en ese orden, separados por una coma, como en (3, −10.5). Así, el origen tiene coordenadas (0, 0), y los puntos en los semiejes positivos, a una unidad del origen, tienen coordenadas (1, 0) y (0, 1).

En matemáticas, física e ingeniería, el primer eje suele definirse o representarse como horizontal y orientado hacia la derecha, y el segundo eje es vertical y orientado hacia arriba. (Sin embargo, en algunos contextos de gráficos por computadora, el eje de ordenadas puede estar orientado hacia abajo). El origen a menudo se denomina O y las dos coordenadas a menudo se indican con las letras X y Y, o x y y. Los ejes pueden denominarse eje X y eje Y. Las elecciones de letras provienen de la convención original, que consiste en utilizar la última parte del alfabeto para indicar valores desconocidos. La primera parte del alfabeto se utilizó para designar valores conocidos.

Un plano euclidiano con un sistema de coordenadas cartesianas elegido se denomina plano cartesiano . En un plano cartesiano se pueden definir representantes canónicos de ciertas figuras geométricas, como el círculo unitario (con radio igual a la unidad de longitud y centro en el origen), el cuadrado unitario (cuya diagonal tiene extremos en (0, 0) y (1, 1)), la hipérbola de la unidad, etc.

Los dos ejes dividen el plano en cuatro ángulos rectos, llamados cuadrantes. Los cuadrantes se pueden nombrar o numerar de varias formas, pero el cuadrante en el que todas las coordenadas son positivas generalmente se denomina primer cuadrante.

Si las coordenadas de un punto son (x, y), entonces sus distancias desde el El eje X y desde el eje Y son |y| y |x|, respectivamente; donde | · | denota el valor absoluto de un número.

Tres dimensiones

Un sistema tridimensional de coordenadas cartesianas, con origen O y líneas de eje X, Y y Z, orientado como se muestra por las flechas. Las marcas de garrapata en los ejes son una unidad de longitud separada. El punto negro muestra el punto con coordenadas x = 2, Sí. = 3, y z = 4, o (2, 3, 4).

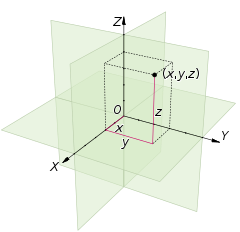
Un sistema de coordenadas cartesianas para un espacio tridimensional consta de un triplete ordenado de líneas (los ejes) que pasan por un punto común (el origen), y son pares perpendiculares; una orientación para cada eje; y una sola unidad de longitud para los tres ejes. Como en el caso bidimensional, cada eje se convierte en una recta numérica. Para cualquier punto P del espacio, uno considera un hiperplano a través de P perpendicular a cada eje de coordenadas, e interpreta el punto donde ese hiperplano corta el eje como un número. Las coordenadas cartesianas de P son esos tres números, en el orden elegido. La construcción inversa determina el punto P dadas sus tres coordenadas.

Alternativamente, cada coordenada de un punto P puede tomarse como la distancia de P al hiperplano definido por los otros dos ejes, con el signo determinado por la orientación del eje correspondiente.

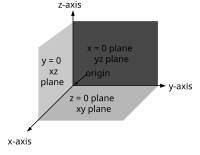
Cada par de ejes define un hiperplano de coordenadas. Estos hiperplanos dividen el espacio en ocho octantes. Los octantes son:

()+x,+Sí.,+z)()− − x,+Sí.,+z)()+x,− − Sí.,+z)()+x,+Sí.,− − z)()+x,− − Sí.,− − z)()− − x,+Sí.,− − z)()− − x,− − Sí.,+z)()− − x,− − Sí.,− − z){displaystyle {begin{aligned}(+x,+y,+z) reducida(-x,+y,+z) limitada(+x,-y,+z) limitada(+x,+x,-y,-z)(+x,-y,-z) distante(-x,+y,-z)

Las coordenadas generalmente se escriben como tres números (o fórmulas algebraicas) entre paréntesis y separados por comas, como en (3, −2.5, 1) o (t, u + v, π/2). Por lo tanto, el origen tiene coordenadas (0, 0, 0), y los puntos unitarios en los tres ejes son (1, 0, 0) , (0, 1, 0) y (0, 0, 1).

No hay nombres estándar para las coordenadas en los tres ejes (sin embargo, a veces se usan los términos abscisa, ordenada y aplicar). Las coordenadas a menudo se indican con las letras X, Y y Z, o x, y y z. Los ejes pueden denominarse eje X, eje Y y eje Z, respectivamente. Entonces, los hiperplanos de coordenadas pueden denominarse plano XY, plano YZ y plano XZ.

En contextos de matemáticas, física e ingeniería, los primeros dos ejes a menudo se definen o representan como horizontales, con el tercer eje apuntando hacia arriba. En ese caso, la tercera coordenada puede llamarse altura o altitud. La orientación generalmente se elige de modo que el ángulo de 90 grados desde el primer eje hasta el segundo eje se vea en sentido contrario a las agujas del reloj cuando se ve desde el punto (0, 0, 1); una convención que comúnmente se llama la regla de la mano derecha.

Las superficies de las coordenadas cartesianas ()x, Sí., z). El z-eje es vertical y el x-eje se destaca en verde. Así, el hiperplano rojo muestra los puntos con x = 1, el hiperplano azul muestra los puntos con z = 1, y el hiperplano amarillo muestra los puntos con Sí. = 1 -. Las tres superficies se intersectan en el punto P (shown como esfera negra) con las coordenadas cartesianas (1 −1, 1).

Dimensiones más altas

Puesto que las coordenadas cartesianas son únicas y no ambiguas, los puntos de un plano cartesiano se pueden identificar con pares de números reales; es decir, con el producto cartesiano R2=R× × R{displaystyle mathbb {R} {2}=Mathbb {R} times mathbb {R}, donde R{displaystyle mathbb {R} es el conjunto de todos los números reales. Del mismo modo, los puntos en cualquier espacio euclidiano de dimensión n ser identificado con los tuples (listas) n números reales; es decir, con el producto cartesiano Rn{displaystyle mathbb {R} {} {}} {fn}}.

Generalizaciones

El concepto de coordenadas cartesianas se generaliza para permitir ejes que no son perpendiculares entre sí y/o diferentes unidades a lo largo de cada eje. En ese caso, cada coordenada se obtiene proyectando el punto sobre un eje en una dirección paralela al otro eje (o, en general, al hiperplano definido por todos los demás ejes). En un sistema de coordenadas oblicuas de este tipo, los cálculos de distancias y ángulos deben modificarse con respecto a los sistemas cartesianos estándar, y muchas fórmulas estándar (como la fórmula de Pitágoras para la distancia) no se cumplen (ver plano afín).

Notaciones y convenciones

Las coordenadas cartesianas de un punto se suelen escribir entre paréntesis y separadas por comas, como en (10, 5) o (3, 5, 7). El origen a menudo se etiqueta con la letra mayúscula O. En la geometría analítica, las coordenadas desconocidas o genéricas a menudo se indican con las letras (x, y) en el plano y (x, y, z) en el espacio tridimensional. Esta costumbre proviene de una convención de álgebra, que usa letras cerca del final del alfabeto para valores desconocidos (como las coordenadas de puntos en muchos problemas geométricos) y letras cerca del principio para cantidades dadas.

Estos nombres convencionales se usan a menudo en otros dominios, como la física y la ingeniería, aunque se pueden usar otras letras. Por ejemplo, en un gráfico que muestre cómo varía la presión con el tiempo, las coordenadas del gráfico se pueden indicar como p y t. Cada eje suele llevar el nombre de la coordenada que se mide a lo largo de él; entonces uno dice el eje x, el eje y, el eje t, etc.

Otra convención común para nombrar coordenadas es usar subíndices, como (x₁, x₂,..., x_n) para las coordenadas n en un n- espacio dimensional, especialmente cuando n es mayor que 3 o no especificado. Algunos autores prefieren la numeración (x₀, x₁,..., x_n−1). Estas notaciones son especialmente ventajosas en la programación de computadoras: al almacenar las coordenadas de un punto como una matriz, en lugar de un registro, el subíndice puede servir para indexar las coordenadas.

En ilustraciones matemáticas de sistemas cartesianos bidimensionales, la primera coordenada (tradicionalmente llamada abscisa) se mide a lo largo de un eje horizontal, orientado de izquierda a derecha. La segunda coordenada (la ordenada) se mide a lo largo de un eje vertical, generalmente orientado de abajo hacia arriba. Los niños pequeños que aprenden el sistema cartesiano suelen aprender el orden para leer los valores antes de consolidar los conceptos de los ejes x-, y- y z, comenzando con mnemónicos 2D (por ejemplo, 'Camina por el pasillo y luego sube las escaleras' similar a cruzar el eje x y luego subir verticalmente a lo largo de y-eje).

Sin embargo, los gráficos por computadora y el procesamiento de imágenes a menudo usan un sistema de coordenadas con el eje y orientado hacia abajo en la pantalla de la computadora. Esta convención se desarrolló en la década de 1960 (o antes) a partir de la forma en que las imágenes se almacenaban originalmente en los búferes de visualización.

Para los sistemas tridimensionales, una convención es representar el plano xy horizontalmente, con el eje z agregado para representar la altura (positivo hacia arriba). Además, existe una convención para orientar el eje x hacia el espectador, sesgado hacia la derecha o hacia la izquierda. Si un diagrama (proyección 3D o dibujo en perspectiva 2D) muestra los ejes x e y horizontal y verticalmente, respectivamente, entonces el z- el eje debe mostrarse apuntando "fuera de la página" hacia el espectador o la cámara. En un diagrama 2D de este tipo de un sistema de coordenadas 3D, el eje z aparecería como una línea o un rayo apuntando hacia abajo y hacia la izquierda o hacia abajo y hacia la derecha, dependiendo de la perspectiva del espectador o de la cámara.. En cualquier diagrama o pantalla, la orientación de los tres ejes, como un todo, es arbitraria. Sin embargo, la orientación de los ejes entre sí siempre debe cumplir con la regla de la mano derecha, a menos que se indique específicamente lo contrario. Todas las leyes de la física y las matemáticas asumen este carácter diestro, lo que garantiza la coherencia.

Para diagramas 3D, los nombres " abscissa " y " Ordenate " rara vez se usan para x y y , respectivamente. Cuando son, el z -coordenate a veces se llama aplicate . Las palabras abscisa , ordinate y aplican a veces se utilizan para referirse a los ejes de coordenadas en lugar de los valores de coordenadas.

Cuadrantes y octantos

Los cuatro cuadrantes de un sistema de coordenadas cartesiano

Los ejes de un sistema cartesiano bidimensional dividen el plano en cuatro regiones infinitas, llamados cuadrantes , cada uno limitado por dos medios ejes. Estos a menudo están numerados del 1 al 4 y denotados por los números romanos: I (donde las coordenadas tienen signos positivos), II (donde la abscisa es negativa - y la ordenada es positiva +), III (donde tanto la abscisa como la ordenada son -) y IV (abscisa +, ordenado -). Cuando los ejes se dibujan de acuerdo con la costumbre matemática, la numeración va en sentido antihorario a partir de la parte superior derecha (" cuadrante noreste ").

Del mismo modo, un sistema cartesiano tridimensional define una división del espacio en ocho regiones o octantantes , según los signos de las coordenadas de los puntos. La convención utilizada para nombrar a un octante específico es enumerar sus señales; Por ejemplo, (+ + +) o (- + -) . La generalización del cuadrante y el octante a un número arbitrario de dimensiones es el ortante , y se aplica un sistema de nombres similar.

fórmulas cartesianas para el avión

Distancia entre dos puntos

La distancia euroclidiana entre dos puntos del avión con coordenadas cartesianas ()x1,Sí.1){displaystyle (x_{1},y_{1}} y ()x2,Sí.2){displaystyle (x_{2},y_{2}} es

d=()x2− − x1)2+()Sí.2− − Sí.1)2.{displaystyle d={sqrt {(x_{2}-x_{1}}{2}+(y_{2}-y_{1}}}}}

Esta es la versión cartesiana del teorema de Pitágoras. En espacio tridimensional, la distancia entre puntos ()x1,Sí.1,z1){displaystyle (x_{1},y_{1},z_{1}} y ()x2,Sí.2,z2){displaystyle (x_{2},y_{2},z_{2}} es

d=()x2− − x1)2+()Sí.2− − Sí.1)2+()z2− − z1)2,{displaystyle d={sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1}}}}} {2}}}}}}}}}}}}}}

que se puede obtener mediante dos aplicaciones consecutivas de Pythágoras ' teorema.

transformaciones euclidianas

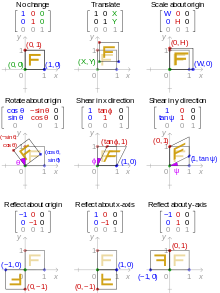
Las transformaciones euclidianas o los movimientos euclidianos son las asignaciones (bijetivas) de puntos del plano euclidiano a sí mismos que preservan distancias entre puntos. Hay cuatro tipos de estas asignaciones (también llamadas isometrías): traducciones, rotaciones, reflexiones y reflejos de deslizamiento.

traducción

Traducir un conjunto de puntos del plano, preservando las distancias y direcciones entre ellos, es equivalente a agregar un par fijo de números ( a , , b ) a las coordenadas cartesianas de cada punto del conjunto. Es decir, si las coordenadas originales de un punto son ( x , y ) , después de la traducción serán

()x.,Sí..)=()x+a,Sí.+b).{displaystyle (x',y')=(x+a,y+b). }

Rotación

Para girar una figura en sentido contrario alrededor del origen por algún ángulo Silencio Silencio {displaystyle theta } es equivalente a reemplazar cada punto por coordenadas (x,Sí.) por el punto con coordenadas (x ',Sí. '), donde

x.=x#⁡ ⁡ Silencio Silencio − − Sí.pecado⁡ ⁡ Silencio Silencio Sí..=xpecado⁡ ⁡ Silencio Silencio +Sí.#⁡ ⁡ Silencio Silencio .{displaystyle {begin{aligned}x'ciendo=xcos theta -ysin theta \y' recur=xsin theta Y 'cos theta.

Así:

()x.,Sí..)=()()x#⁡ ⁡ Silencio Silencio − − Sí.pecado⁡ ⁡ Silencio Silencio ),()xpecado⁡ ⁡ Silencio Silencio +Sí.#⁡ ⁡ Silencio Silencio )).{displaystyle (x',y')=(xcos theta -ysin theta ,),(xsin theta +ycos theta ,)}

Reflexión

Si ()x, Sí.) son las coordenadas cartesianas de un punto, entonces () -x, Sí.) son las coordenadas de su reflejo a través del segundo eje de coordenadas (el eje y), como si esa línea fuera un espejo. Igualmente, ()x, −Sí.) son las coordenadas de su reflejo a través del primer eje de coordenadas (el eje x). En mayor generalidad, la reflexión a través de una línea a través del origen haciendo un ángulo Silencio Silencio {displaystyle theta } con el eje x, es equivalente a reemplazar cada punto por coordenadas ()x, Sí.) por el punto con coordenadas ()x′,Sí.′), donde

x.=x#⁡ ⁡ 2Silencio Silencio +Sí.pecado⁡ ⁡ 2Silencio Silencio Sí..=xpecado⁡ ⁡ 2Silencio Silencio − − Sí.#⁡ ⁡ 2Silencio Silencio .{displaystyle {begin{aligned}x'ciendo=xcos 2theta +ysin 2theta \y'ciendo=xsin 2theta -ycos 2theta.

Así:

()x.,Sí..)=()()x#⁡ ⁡ 2Silencio Silencio +Sí.pecado⁡ ⁡ 2Silencio Silencio ),()xpecado⁡ ⁡ 2Silencio Silencio − − Sí.#⁡ ⁡ 2Silencio Silencio )).{displaystyle (x',y')=(xcos 2theta +ysin 2theta ,),(xsin 2theta -ycos 2theta ,)}

Reflexión de deslizamiento

Una reflexión de deslizamiento es la composición de una reflexión a través de una línea seguida de una traducción en la dirección de esa línea. Se puede ver que el orden de estas operaciones no importa (la traducción puede ser lo primero, seguido de la reflexión).

Forma de matriz general de las transformaciones

Todas las transformaciones afines del avión se pueden describir de forma uniforme usando matrices. Para ello las coordenadas ()x,Sí.){displaystyle (x,y)} de un punto se representan comúnmente como la matriz de columna ()xSí.).{displaystyle {begin{pmatrix}xyend{pmatrix}}} El resultado ()x.,Sí..){displaystyle (x',y')} de aplicar una transformación afinada a un punto ()x,Sí.){displaystyle (x,y)} es dado por la fórmula

()x.Sí..)=A()xSí.)+b,{displaystyle {begin{pmatrix}x'y'end{pmatrix}=A{begin{pmatrix}x\yend{pmatrix}+b,}

A=()A1,1A1,2A2,1A2,2){displaystyle A={begin{pmatrix}A_{1,1} {1,2}A_{2,1} {2}end{pmatrix}}

b=()b1b2){displaystyle b={begin{pmatrix}b_{1}b_{2}end{pmatrix}}

x.=xA1,1+Sí.A1,1+b1Sí..=xA2,1+Sí.A2,2+b2.{displaystyle {begin{aligned}x' limit=xA_{1,1}+yA_{1,1}+b_{1}\\\y' limit=xA_{2,1}+yA_{2,2}+b_{2}end{aligned}}}}}}}}}}}}

Entre las transformaciones afines, las transformaciones euclidianas se caracterizan por el hecho de que la matriz A{displaystyle A} es ortogonal; es decir, sus columnas son vectores ortogonales de la norma Euclideana, o, explícitamente,

A1,1A1,2+A2,1A2,2=0{displaystyle A_{1,1}A_{1,2}+A_{2,1}A_{2,2}=0}

A1,12+A2,12=A1,22+A2,22=1.{displaystyle A_{1,1}{2}+A_{2,1} {2}=A_{1,2}{2}+A_{2,2}^{2}=1.}

Esto es equivalente a decir que a veces su transposición es la matriz de identidad. Si estas condiciones no se mantienen, la fórmula describe una transformación afina más general.

La transformación es una traducción si y solo si a es la matriz de identidad. La transformación es una rotación alrededor de algún punto si y solo si a es una matriz de rotación, lo que significa que es ortogonal y

A1,1A2,2− − A2,1A1,2=1.{displaystyle A_{1,1}A_{2,2}-A_{2,1}A_{1,2}=1.

se obtiene un reflejo de reflexión o deslizamiento cuando,

A1,1A2,2− − A2,1A1,2=− − 1.{displaystyle A_{1,1}A_{2,2}-A_{2,1}A_{1,2}=-1.}

Suponiendo que las traducciones no se utilicen (es decir, b1=b2=0{displaystyle B_{1}=b_{2}=0}) transformaciones se pueden componer simplemente multiplicando las matrices de transformación asociadas. En el caso general, es útil utilizar la matriz aumentada de la transformación; es decir, reescribir la fórmula de transformación

()x.Sí..1)=A.()xSí.1),{fnMicrosoftware}=A'{begin{pmatrix}xy1end{pmatrix}}=A'{begin{pmatrix}xy1end{pmatrix}}}

A.=()A1,1A1,2b1A2,1A2,2b2001).{displaystyle A'={begin{pmatrix}A_{1,1} limitA_{1,2} limitb_{1}\A_{2,1} {2} {2} {b_{2}} 3end{pmatrix}}

transformación afina

Efecto de la aplicación de varias matrices de transformación de afinas 2D en un cuadrado de unidad (las reflexiones son casos especiales de escalado)

Las transformaciones afines del plano euclidiano son transformaciones que asignan líneas a líneas, pero pueden cambiar distancias y ángulos. Como se dijo en la sección anterior, pueden representarse con matrices aumentadas:

()A1,1A2,1b1A1,2A2,2b2001)()xSí.1)=()x.Sí..1).{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {}} {}}} {cH0} {cH0} {cH0} {cH0}cH00}cH00}cH00}cH0}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH0cH0}cH00cH00}cH00}cH00}cH0cH00}cH00}cH00}cH00}cH00cH00}cH00cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH

Las transformaciones euclidianas son las transformaciones afines tal que la matriz 2×2 de la Ai,j{displaystyle A_{i,j} es ortogonal.

La matriz aumentada que representa la composición de dos transformaciones afines se obtiene multiplicando sus matrices aumentadas.

Algunas transformaciones afines que no son transformaciones euclidianas han recibido nombres específicos.

escala

Un ejemplo de una transformación afina que no es euclidiana es dado por escala. Hacer una cifra más grande o más pequeña es equivalente a multiplicar las coordenadas cartesianas de cada punto por el mismo número positivo m . If ( x , y ) son las coordenadas de un punto en la figura original, el punto correspondiente en la figura escalada tiene coordenadas

()x.,Sí..)=()mx,mSí.).{displaystyle (x',y')=(mx,my). }

if m es mayor que 1, la figura se hace más grande; Si m está entre 0 y 1, se vuelve más pequeño.

Shearing

Una transformación de cizallamiento empujará la parte superior de un lado cuadrado para formar un paralelogramo. El cizallamiento horizontal se define por:

()x.,Sí..)=()x+Sí.s,Sí.){displaystyle (x',y')=(x+ys,y)}

El cizallamiento también se puede aplicar verticalmente:

()x.,Sí..)=()x,xs+Sí.){displaystyle (x',y')=(x,xs+y)}

Orientación y mano

en dos dimensiones

La regla de la mano derecha

Arreglar o elegir el eje x --Axis determina el y -xis hasta la dirección. A saber, el eje y ----Ansis es necesariamente el perpendicular al x --alxis a través del punto marcado 0 en el x -xis. Pero hay una elección de las dos medias líneas en la perpendicular para designar como positiva y cuáles como negativas. Cada una de estas dos opciones determina una orientación diferente (también llamada Handedness ) del plano cartesiano.

La forma habitual de orientar el plano, con el eje x positivo apuntando a la derecha y el positivo y -exis apuntando hacia arriba (y el x -exis es el " primero " y el y -axis el " segundo " eje), se considera el positivo o orientación estándar , también llamada orientación diestra .

Una mnemónica comúnmente utilizada para definir la orientación positiva es la regla de la derecha . Colocando una mano derecha algo cerrada en el plano con el pulgar apuntando hacia arriba, los dedos apuntan desde el eje x --eje al eje y --eje, en un sistema de coordenadas orientado positivamente.

La otra forma de orientar el plano está siguiendo la regla de la mano izquierda , colocando la mano izquierda en el avión con el pulgar apuntando hacia arriba.

Al apuntar el pulgar lejos del origen a lo largo de un eje hacia positivo, la curvatura de los dedos indica una rotación positiva a lo largo de ese eje.

Independientemente de la regla utilizada para orientar el plano, girar el sistema de coordenadas preservará la orientación. Cambiar cualquier eje revertirá la orientación, pero el cambio de ambos dejará la orientación sin cambios.

en tres dimensiones

Fig. 7 – La orientación zurda se muestra a la izquierda, y la derecha a la derecha.

Fig. 8 – El sistema de coordenadas cartesiano de mano derecha que indica los planos de coordenadas.

Una vez que se especifican x -y y --Axes, determinan la línea a lo largo de la cual debe estar el eje z ---xis, pero allí son dos posibles orientación para esta línea. Los dos posibles sistemas de coordenadas que resultado se llaman ' diestro ' y ' zurdo '. La orientación estándar, donde el plano xy es horizontal y el z -exis señala (y el x -y el y y el y -Axis forma un sistema de coordenadas bidimensional orientado positivamente en el plano xy --Plane si se observa desde arriba el xy -plano) se llama diestro o positivo .

Cobertura cartesiana 3D

El nombre deriva de la regla de la derecha. Si el dedo índice de la mano derecha se apunta hacia adelante, el dedo medio doblado hacia adentro en ángulo recto y el pulgar colocado en ángulo recto a ambos, los tres dedos indican la orientación relativa de x -, y -y z -axes en un sistema diestro . El pulgar indica el x -xis, el dedo índice el y -xis y el dedo medio el z -axis. Por el contrario, si lo mismo se hace con la mano izquierda, se produce un sistema zurdo.

La Figura 7 representa un sistema de coordenadas izquierdo y diestro. Porque se representa un objeto tridimensional en la pantalla bidimensional, el resultado de la distorsión y la ambigüedad. El eje que apunta hacia abajo (y hacia la derecha) también está destinado a apuntar hacia el observador, mientras que el eje de "-Middle " -es está destinado a apuntar lejos del observador. El círculo rojo es paralelo al plan de xy -xy e indica rotación del x -xis al y -Axis (en ambos casos). Por lo tanto, la flecha roja pasa frente a el z -exis.

La Figura 8 es otro intento de representar un sistema de coordenadas diestro. Nuevamente, existe una ambigüedad causada por proyectar el sistema de coordenadas tridimensional en el plano. Muchos observadores ven la Figura 8 como " volteando y fuera " entre un cubo convexo y un cóncavo " esquina ". Esto corresponde a las dos posibles orientaciones del espacio. Ver la figura como convexo ofrece un sistema de coordenadas zurdos. Así, el " correcto " La forma de ver la Figura 8 es imaginar el eje x --Axis como apuntando hacia el observador y, por lo tanto, viendo una esquina cóncava.

representando un vector en la base estándar

Un punto en el espacio en un sistema de coordenadas cartesiano también puede ser representado por un vector de posición, que se puede considerar como una flecha apuntando desde el origen del sistema de coordenadas hasta el punto. Si las coordenadas representan posiciones espaciales (desplazamientos), es común representar el vector desde el origen hasta el punto de interés como r{displaystyle mathbf {r}. En dos dimensiones, el vector desde el origen hasta el punto con coordenadas cartesianas (x, y) puede ser escrito como:

r=xi+Sí.j,{displaystyle mathbf {r} =xmathbf {i} Y Mathbf {j}

Donde i=()10){displaystyle mathbf {i} {begin{pmatrix}1end{pmatrix}} y j=()01){displaystyle mathbf {j} {begin{pmatrix}01end{pmatrix}}} son vectores de unidad en la dirección de la x-eje y Sí.-eje respectivamente, generalmente referido como el Bases estándar (en algunas áreas de aplicación, éstas también pueden ser referidas como revisores). Del mismo modo, en tres dimensiones, el vector desde el origen hasta el punto con coordenadas cartesianas ()x,Sí.,z){displaystyle (x,y,z)} puede ser escrito como:

r=xi+Sí.j+zk,{displaystyle mathbf {r} =xmathbf {i} Y Mathbf {j} - No.

Donde i=()100),{displaystyle mathbf {i} = {begin{pmatrix}1end{pmatrix}}} j=()010),{displaystyle mathbf {j} ={begin{pmatrix}01end{pmatrix}}}} y k=()001).{displaystyle mathbf {k} ={begin{pmatrix}01end{pmatrix}}}

No hay Interpretación natural de los vectores multiplicadores para obtener otro vector que funcione en todas las dimensiones, sin embargo, hay una manera de usar números complejos para proporcionar dicha multiplicación. En un plano cartesiano bidimensional, identifique el punto con coordenadas ( x , y ) con el número complejo z = x + iy . Aquí, i es la unidad imaginaria y se identifica con el punto con coordenadas (0, 1) , por lo que es no El vector unitario en la dirección del x -exis. Dado que los números complejos se pueden multiplicar dando otro número complejo, esta identificación proporciona un medio para " multiplicar " vectores. En un espacio cartesiano tridimensional se puede hacer una identificación similar con un subconjunto de los cuaterniones.

aplicaciones

Las coordenadas cartesianas son una abstracción que tiene una multitud de posibles aplicaciones en el mundo real. Sin embargo, tres pasos constructivos están involucrados en la superposición de coordenadas en una aplicación de problemas.

1. Las unidades de distancia deben decidir definir el tamaño espacial representado por los números utilizados como coordenadas.
2. Un origen debe ser asignado a una ubicación espacial específica o un hito, y
3. la orientación de los ejes debe definirse usando cues direccionales disponibles para todos menos un eje.

Considere como un ejemplo superponiendo las coordenadas cartesianas 3D sobre todos los puntos en la tierra (es decir, 3D geoespacial). Los kilómetros son una buena opción de unidades, ya que la definición original del kilómetro era geoespacial, con 10,000 km igualando la distancia de la superficie desde el ecuador hasta el Polo Norte. Basado en la simetría, el centro gravitacional de la tierra sugiere una ubicación natural del origen (que se puede detectar a través de órbitas satelitales). El eje de la rotación de la Tierra proporciona una orientación natural para los ejes x , y y z , fuertemente asociados con " arriba vs. Down ", tan positivo z puede adoptar la dirección desde el geocentro hasta el Polo Norte. Se necesita una ubicación en el ecuador para definir el eje x --Axis, y el meridiano principal se destaca como una orientación de referencia, por lo que el eje x ---eje toma la orientación del geocentro Out to 0 grados longitude, 0 grados latitud. Tenga en cuenta que con tres dimensiones, y dos orientaciones de ejes perpendiculares fijadas para x y z , el eje y ---Axis está determinado por las dos primeras opciones. Para obedecer la regla de la mano derecha, el eje y ----Amis debe señalar desde el geocentro a < 90 grados longitud, 0 grados latitud. Desde una longitud de −73.985 656 grados , una latitud 40.748 433 grados y un radio de tierra de 40,000/2 π km, y transformándose de coordenadas esféricas a cartesianas, se pueden estimar las coordenadas geocéntricas del Empire State Building, ( x , y , z ) = ( 1,330.53 km , 4,635.75 km , 4,155.46 km ) . La navegación GPS se basa en tales coordenadas geocéntricas.

En proyectos de ingeniería, el acuerdo sobre la definición de coordenadas es una base crucial. No se puede suponer que las coordenadas vienen predefinidas para una aplicación novedosa, por lo que el conocimiento de cómo erigir un sistema de coordenadas donde anteriormente no había tal sistema de coordenadas es esencial para aplicar René Descartes ' pensando.

Si bien las aplicaciones espaciales emplean unidades idénticas a lo largo de todos los ejes, en aplicaciones comerciales y científicas, cada eje puede tener diferentes unidades de medición asociadas con ella (como kilogramos, segundos, libras, etc.). Aunque los espacios de cuatro y dimensiones superiores son difíciles de visualizar, el álgebra de las coordenadas cartesianas se puede extender relativamente fácilmente a cuatro o más variables, por lo que se pueden hacer ciertos cálculos que involucran muchas variables. (Este tipo de extensión algebraica es lo que se usa para definir la geometría de espacios de dimensiones más altas). Por el contrario, a menudo es útil usar la geometría de las coordenadas cartesianas en dos o tres dimensiones para visualizar las relaciones algebraicas entre dos o tres de muchos no -Calvarias spaciales.

El gráfico de una función o relación es el conjunto de todos los puntos que satisfacen esa función o relación. Para una función de una variable, f , el conjunto de todos los puntos ( x , y ) , donde y = f ( x ) es el gráfico de la función f . Para una función g de dos variables, el conjunto de todos los puntos ( x , y , z ) , donde z = g ( x , y ) es el gráfico de la función g . Un bosquejo de la gráfica de dicha función o relación consistiría en todas las partes sobresalientes de la función o relación que incluiría su extremo relativo, su concavidad y puntos de inflexión, cualquier punto de discontinuidad y su comportamiento final. Todos estos términos están más definidos en el cálculo. Dichos gráficos son útiles en el cálculo para comprender la naturaleza y el comportamiento de una función o relación.