Sistema de control difuso

Un sistema de control difuso es un sistema de control basado en lógica difusa, un sistema matemático que analiza los valores de entrada analógica en términos de variables lógicas que toman valores continuos entre 0 y 1, en contraste con el clásico o lógica digital, que opera con valores discretos de 1 o 0 (verdadero o falso, respectivamente).

Resumen

La lógica difusa se usa mucho en el control de máquinas. El término "borroso" se refiere al hecho de que la lógica involucrada puede manejar conceptos que no pueden expresarse como "verdadero" o "falso" sino más bien como "parcialmente cierto". Aunque los enfoques alternativos, como los algoritmos genéticos y las redes neuronales, pueden funcionar tan bien como la lógica difusa en muchos casos, la lógica difusa tiene la ventaja de que la solución al problema se puede expresar en términos que los operadores humanos puedan entender, de modo que su experiencia pueda ser utilizado en el diseño del controlador. Esto facilita la mecanización de tareas que los humanos ya realizan con éxito.

Historia y aplicaciones

La lógica difusa fue propuesta por Lotfi A. Zadeh de la Universidad de California en Berkeley en un artículo de 1965. Explicó sus ideas en un artículo de 1973 que introdujo el concepto de "variables lingüísticas", que en este artículo equivale a una variable definida como un conjunto borroso. Siguieron otras investigaciones, con la primera aplicación industrial, un horno de cemento construido en Dinamarca, que entró en funcionamiento en 1975.

Los sistemas difusos se implementaron inicialmente en Japón.

• Seiji Yasunobu y Soji Miyamoto de Hitachi, que en 1985 proporcionaron simulaciones que demostraron la viabilidad de sistemas de control borrosos para el metro de Sendai. Sus ideas fueron adoptadas, y los sistemas borrosos se utilizaron para controlar la aceleración, frenado y parar cuando la Línea Namboku abrió en 1987.
• En 1987, Takeshi Yamakawa demostró el uso del control borroso, a través de un conjunto de simples chips de lógica borrosa dedicados, en un experimento de "pendulum invertido". Este es un problema de control clásico, en el que un vehículo intenta mantener un poste montado en su parte superior por una bisagra vertical moviéndose hacia atrás y hacia adelante. Yamakawa posteriormente hizo la demostración más sofisticada al montar una copa de vino que contiene agua e incluso un ratón vivo en la parte superior del péndulo: el sistema mantuvo la estabilidad en ambos casos. Yamakawa eventualmente continuó organizando su propio laboratorio de investigación de sistemas fuzzy para ayudar a explotar sus patentes en el campo.
• Posteriormente, los ingenieros japoneses desarrollaron una amplia gama de sistemas borrosos tanto para aplicaciones industriales como para consumidores. En 1988 Japón estableció el Laboratorio de Ingeniería Internacional Fuzzy (LIFE), un acuerdo de cooperación entre 48 empresas para realizar investigaciones borrosas. La empresa automotriz Volkswagen fue el único miembro corporativo extranjero de LIFE, enviando un investigador durante tres años.
• Los bienes de consumo japoneses a menudo incorporan sistemas borrosos. Las aspiradoras de Matsushita utilizan microcontroladores que ejecutan algoritmos borrosos para interrogar sensores de polvo y ajustar el poder de succión en consecuencia. Las máquinas de lavado Hitachi utilizan controladores borrosos para sensores de peso, tejido-mix y suciedad y establecen automáticamente el ciclo de lavado para el mejor uso de potencia, agua y detergente.
• Canon desarrolló una cámara de enfoque automático que utiliza un dispositivo de carga (CCD) para medir la claridad de la imagen en seis regiones de su campo de visión y utilizar la información proporcionada para determinar si la imagen está en foco. También rastrea la tasa de cambio de movimiento de lentes durante el enfoque, y controla su velocidad para prevenir la sobresuelción. El sistema de control borroso de la cámara utiliza 12 entradas: 6 para obtener los datos de claridad actuales proporcionados por la CCD y 6 para medir la tasa de cambio de movimiento de lentes. La salida es la posición de la lente. El sistema de control borroso utiliza 13 reglas y requiere 1,1 kilobytes de memoria.
• Un aire acondicionado industrial diseñado por Mitsubishi utiliza 25 reglas de calefacción y 25 reglas de refrigeración. Un sensor de temperatura proporciona entrada, con salidas de control alimentadas a un inversor, una válvula de compresión y un motor de ventilador. En comparación con el diseño anterior, el controlador borroso calienta y se enfría cinco veces más rápido, reduce el consumo de energía en un 24%, aumenta la estabilidad de temperatura por un factor de dos, y utiliza menos sensores.
• Otras aplicaciones investigadas o implementadas incluyen: reconocimiento de carácter y escritura; sistemas de fuzzy ópticos; robots, incluyendo uno para hacer arreglos de flores japonesas; helicópteros robot controlados por voz (el empuje es un "acto de equilibrio" más bien similar al problema del péndulo invertido); robótica de rehabilitación para proporcionar soluciones específicas para el paciente (por ejemplo, para controlar la frecuencia cardíaca y la presión arterial); control de flujo de polvos en la fabricación de película; sistemas de ascensor; etc.

También se está trabajando en sistemas difusos en América del Norte y Europa, aunque a una escala menos extensa que en Japón.

• La Agencia de Protección Ambiental de EE.UU. ha investigado el control borroso para motores eficientes en energía, y la NASA ha estudiado el control borroso para el acoplamiento automatizado del espacio: las simulaciones muestran que un sistema de control borroso puede reducir considerablemente el consumo de combustible.
• Firmas como Boeing, General Motors, Allen-Bradley, Chrysler, Eaton y Whirlpool han trabajado en lógica borrosa para su uso en frigoríficos de baja potencia, transmisiones automotrices mejoradas y motores eléctricos eficientes en energía.
• En 1995 Maytag introdujo un lavaplatos "inteligente" basado en un controlador borroso y un "modulo de detección único" que combina un termistor, para la medición de temperatura; un sensor de conductividad, para medir el nivel de disuasión de los iones presentes en el lavado; un sensor de turbididad que mide la luz dispersa y transmitida para medir el ensuciamiento del lavado; y un sensor magnetostrictivo para leer la velocidad de la columna. El sistema determina el ciclo de lavado óptimo para cualquier carga para obtener los mejores resultados con la menor cantidad de energía, detergente y agua. Incluso se ajusta para los alimentos secos siguiendo la última vez que se abrió la puerta, y estima el número de platos por el número de veces que se abrió la puerta.
• En 2017 Xiera Technologies Inc. desarrolló el primer auto-tuner para la base de conocimiento del controlador lógico borroso conocido como edeX. Esta tecnología fue probada por Mohawk College y fue capaz de resolver problemas multifunción no lineales 2x2 y 3x3 multi-input.

La investigación y el desarrollo también continúan en aplicaciones difusas en software, a diferencia del firmware, el diseño, incluidos los sistemas expertos difusos y la integración de lógica difusa con redes neuronales y la llamada "genética" sistemas de software, con el objetivo final de construir "autoaprendizaje" sistemas de control difuso. Estos sistemas se pueden emplear para controlar plantas dinámicas no lineales complejas, por ejemplo, el cuerpo humano.

Conjuntos borrosos

Las variables de entrada en un sistema de control borroso se asignan en general mediante conjuntos de funciones de pertenencia similares a esta, conocidas como "conjuntos borrosos". El proceso de convertir un valor de entrada nítido en un valor difuso se denomina 'fuzzificación'. Se consideró el enfoque basado en la lógica difusa mediante el diseño de dos sistemas difusos, uno para el ángulo de rumbo del error y el otro para el control de la velocidad.

Un sistema de control también puede tener varios tipos de entradas de interruptor, o "ON-OFF", junto con sus entradas analógicas, y tales entradas de interruptor, por supuesto, siempre tendrán un valor de verdad igual a 1 o 0, pero el esquema puede tratarlos como funciones difusas simplificadas que resultan tener un valor u otro.

Dadas las "asignaciones" de variables de entrada en funciones de pertenencia y valores de verdad, el microcontrolador luego toma decisiones sobre qué acción tomar, en función de un conjunto de "reglas", cada una de la forma:

 Si la temperatura del freno es cálida y la velocidad no es muy rápida
Luego la presión de freno disminuye ligeramente.

En este ejemplo, las dos variables de entrada son "temperatura del freno" y "velocidad" que tienen valores definidos como conjuntos borrosos. La variable de salida, "presión de freno" también está definido por un conjunto difuso que puede tener valores como "estático" o "ligeramente aumentado" o "ligeramente disminuido" etc.

Control difuso en detalle

Los controladores difusos son conceptualmente muy simples. Constan de una etapa de entrada, una etapa de procesamiento y una etapa de salida. La etapa de entrada asigna el sensor u otras entradas, como interruptores, ruedecillas, etc., a las funciones de membresía y valores de verdad apropiados. La etapa de procesamiento invoca cada regla apropiada y genera un resultado para cada una, luego combina los resultados de las reglas. Finalmente, la etapa de salida convierte el resultado combinado nuevamente en un valor de salida de control específico.

La forma más común de las funciones de pertenencia es triangular, aunque también se utilizan curvas trapezoidales y de campana, pero la forma generalmente es menos importante que el número de curvas y su ubicación. De tres a siete curvas son generalmente apropiadas para cubrir el rango requerido de un valor de entrada, o el "universo de discurso" en una jerga confusa.

Como se discutió anteriormente, la etapa de procesamiento se basa en una colección de reglas lógicas en forma de declaraciones IF-THEN, donde la parte IF se denomina "antecedente" y la parte ENTONCES se llama "consecuente". Los sistemas típicos de control difuso tienen docenas de reglas.

Considere una regla para un termostato:

 IF (temperatura es "frío") A continuación gira (el calentador es "alto")

Esta regla usa el valor de verdad de la "temperatura" entrada, que es un valor de verdad de "frío", para generar un resultado en el conjunto borroso para el "calentador" salida, que es un valor de "alto". Este resultado se usa con los resultados de otras reglas para generar finalmente la salida compuesta nítida. Obviamente, cuanto mayor sea el valor de verdad de 'frío', mayor será el valor de verdad de 'alto', aunque esto no significa necesariamente que la salida en sí se establecerá en ' alta" ya que esta es solo una regla entre muchas. En algunos casos, las funciones de membresía pueden ser modificadas por "coberturas" que son equivalentes a los adverbios. Los setos comunes incluyen "alrededor de", "cerca de", "cerca de", "aproximadamente", "muy", & #34;ligeramente", "demasiado", "extremadamente" y "algo". Estas operaciones pueden tener definiciones precisas, aunque las definiciones pueden variar considerablemente entre diferentes implementaciones. "Muy", por ejemplo, funciones de membresía cuadradas; dado que los valores de pertenencia siempre son menores que 1, esto reduce la función de pertenencia. "Extremadamente" reduce al cubo los valores para dar una mayor reducción, mientras que "algo" amplía la función sacando la raíz cuadrada.

En la práctica, los conjuntos de reglas difusas suelen tener varios antecedentes que se combinan mediante operadores difusos, como AND, OR y NOT, aunque nuevamente las definiciones tienden a variar: AND, en una definición popular, simplemente usa el peso mínimo de todos los antecedentes, mientras que OR utiliza el valor máximo. También hay un operador NOT que resta una función de membresía de 1 para dar el "complementario" función.

Hay varias formas de definir el resultado de una regla, pero una de las más comunes y sencillas es la "max-min" método de inferencia, en el que a la función de pertenencia de salida se le da el valor de verdad generado por la premisa.

Las reglas se pueden resolver en paralelo en hardware o secuencialmente en software. Los resultados de todas las reglas que se han activado se "desfuzzifican" a un valor nítido por uno de varios métodos. Hay docenas, en teoría, cada uno con varias ventajas o inconvenientes.

El "centroide" método es muy popular, en el que el "centro de masa" del resultado proporciona el valor nítido. Otro enfoque es la "altura" método, que toma el valor del mayor contribuyente. El método del centroide favorece la regla con la salida de mayor área, mientras que el método de la altura obviamente favorece la regla con el mayor valor de salida.

El siguiente diagrama muestra la inferencia máxima-mínima y la defuzzificación del centroide para un sistema con variables de entrada "x", "y" y "z" y una variable de salida 'n'. Tenga en cuenta que "mu" es la nomenclatura estándar de lógica difusa para "valor de verdad":

Observe cómo cada regla proporciona un resultado como un valor de verdad de una función de pertenencia particular para la variable de salida. En la defuzzificación del centroide, los valores se OR'd, es decir, se utiliza el valor máximo y no se suman los valores, y los resultados se combinan mediante un cálculo del centroide.

El diseño del sistema de control difuso se basa en métodos empíricos, básicamente un enfoque metódico de prueba y error. El proceso general es el siguiente:

• Documente las especificaciones operativas y las entradas y salidas del sistema.
• Documenta los conjuntos borrosos para las entradas.
• Documenta el conjunto de reglas.
• Determinar el método de desactivación.
• Ejecute a través de la suite de pruebas para validar el sistema, ajustar los detalles según sea necesario.
• Documento completo y liberación a la producción.

Como ejemplo general, considere el diseño de un controlador difuso para una turbina de vapor. El diagrama de bloques de este sistema de control es el siguiente:

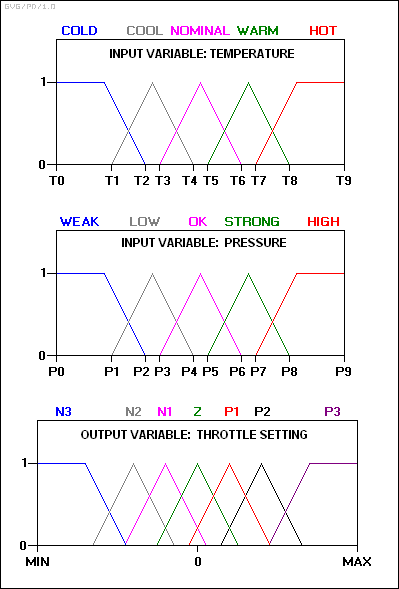
Las variables de entrada y salida se asignan al siguiente conjunto borroso:

- Donde:

 N3: Gran negativo.
N2: Media negativa.
N1: Pequeño negativo.
Cero.
P1: Pequeño positivo.
P2: Medio positivo.
P3: Grande positivo.

El conjunto de reglas incluye reglas como:

Regla 1: Si la temperatura es fresca y la presión es débil,
Entonces el acelerador es P3.

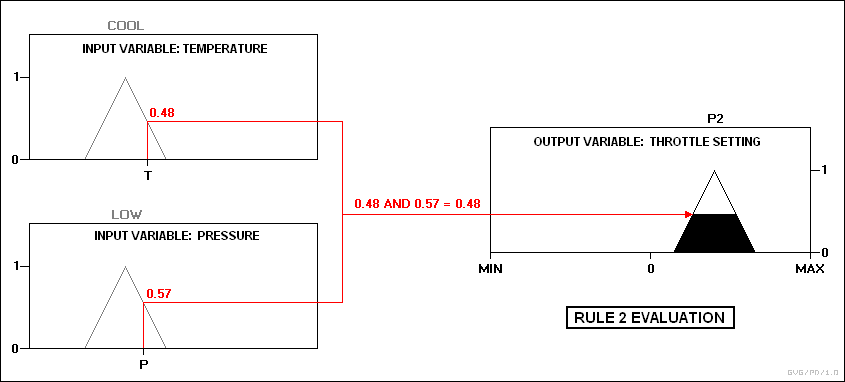
Regla 2: Si la temperatura es fresca y la presión es baja,
Entonces el acelerador es P2.

regla 3: Si la temperatura es fresca y la presión está bien,
Entonces el acelerador es Z.

regla 4: Si la temperatura es fresca y la presión es fuerte,
Entonces el acelerador es N2.

En la práctica, el controlador acepta las entradas y las asigna a sus funciones de pertenencia y valores de verdad. Estas asignaciones luego se introducen en las reglas. Si la regla especifica una relación AND entre las asignaciones de las dos variables de entrada, como lo hacen los ejemplos anteriores, se usa el mínimo de los dos como el valor de verdad combinado; si se especifica un OR, se utiliza el máximo. Se selecciona el estado de salida apropiado y se le asigna un valor de pertenencia al nivel de verdad de la premisa. A continuación, los valores de verdad se desdibujan. Por ejemplo, suponga que la temperatura está en el rango "fresco" y la presión está en el nivel "bajo" y "bien" estados Los valores de presión aseguran que solo se disparen las reglas 2 y 3:

Luego, las dos salidas se eliminan mediante la eliminación del centroide:

 ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

confidencialidad Z P2
1 -+ *
*
*
*
Silencio * 222222222
Silencio * 222222222222
Silencio 3333332222222222222
+---333333222222222222222222222--
^
+150
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

El valor de salida ajustará el acelerador y luego el ciclo de control comenzará nuevamente para generar el siguiente valor.

Construyendo un controlador difuso

Considere implementar con un chip microcontrolador un controlador de retroalimentación simple:

Se define un conjunto borroso para la variable de error de entrada "e", y el cambio de error derivado, "delta", así como la "salida", como sigue:

 LP: gran positivo
SP: pequeño positivo
ZE: cero
SN: pequeño negativo
LN: gran negativo

Si el error oscila entre -1 y +1, con el convertidor de analógico a digital utilizado con una resolución de 0,25, entonces el conjunto borroso de la variable de entrada (que, en este caso, también se aplica a la variable de salida) se puede describir de manera muy simple como una tabla, con los valores de error/delta/salida en la fila superior y los valores de verdad para cada función de membresía dispuestos en filas debajo:

 ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

-1 0,75 -0,5 -0,25 0 0,25 0,25 0,75 0,75 1
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

mu(LP) 0 0 0 0 0 0 0 0 0 0 0,7 1
mu(SP) 0 0 0 0 0 0,3 0,7 0,3 0,7 0,3 0
mu(ZE) 0 0 0 0,3 0,7 0 0 0
mu(SN) 0,3 0,7 0,3 0 0 0
mu(LN) 1 0,7 0 0 0 0 0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ —o, en forma gráfica (donde cada "X" tiene un valor de 0.1):

 LN SN ZE SP LP
+----------------------------------+
Silencio
-1.0 Silencio XXXXXXX XXX::: Silencio
-0.75 Silencio XXXXXXX XXXXXXX::: Silencio
XXXXXXXXXXXX XXX: Silencio
-0.25 Silencio: XXXXXXX XXXXXXX: Silencio
0.0 Silencio: XXX XXXXXXX XXX: Silencio
0,25 Silencio:: XXXXXXX XXXX: Silencio
0,5 Silencio: XXX XXXXXXX XXX XXX 
0,75 Silencio::: XXXXXXX XXXX
1.0 Silencio::: XXX XXXXXXXXXX Silencio
Silencio
+----------------------------------+

Supongamos que este sistema difuso tiene la siguiente base de reglas:

 regla 1: IF e = ZE AND delta = ZE THEN output = ZE
regla 2: IF e = ZE AND delta = SP THEN output = SN
regla 3: IF e = SN AND delta = SN THEN output = LP
regla 4: IF e = LP OR delta = LP THEN salida = LN

Estas reglas son típicas para aplicaciones de control en las que los antecedentes consisten en la combinación lógica de las señales de error y error-delta, mientras que el consecuente es una salida de comando de control. Las salidas de la regla se pueden desfuzzificar mediante un cálculo de centroide discreto:

 SUM(I = 1 TO 4 OF (mu(I) * output(I))) / SUM(I = 1 TO 4 OF mu(I))

Ahora, supongamos que en un momento dado:

 e = 0,25
delta = 0,5

Entonces esto da:

 ____________________________

e delta
____________________________

mu(LP) 0 0.3
mu(SP) 0.7 1
mu(ZE) 0.7 0.3
mu(SN) 0 0
mu(LN) 0 0
____________________________

Conectar esto a la regla 1 da:

 regla 1: IF e = ZE AND delta = ZE THEN output = ZE

mu(1) = MIN(0.7, 0.3) = 0.3
producto(1) = 0

-- donde:

• mu(1): Valor de la verdad de la función de membresía de resultados para la regla 1. En términos de cálculo del centroide, esta es la "masa" de este resultado para este caso discreto.
• Resultado(1): Valor (para la regla 1) donde la función de membresía de resultados (ZE) es máxima sobre el rango de conjunto variable de salida borrosa. Es decir, en términos de cálculo del centroide, la ubicación del "centro de masa" para este resultado individual. Este valor es independiente del valor del "mu". Simplemente identifica la ubicación de ZE a lo largo del rango de salida.

Las otras reglas dan:

 regla 2: IF e = ZE AND delta = SP THEN output = SN

mu 2) = MIN(0,7) = 0,7
producción (2) = 0,5

 regla 3: IF e = SN AND delta = SN THEN output = LP

mu(3) = MIN(0.0, 0.0) = 0
producto(3) = 1

 regla 4: IF e = LP OR delta = LP THEN salida = LN

mu(4) = MAX(0.0, 0.3) = 0.3
producción(4) = 1

El cálculo del centroide produce:

        m u () 1 ) ⋅ ⋅  o u t p u t () 1 ) + m u () 2 ) ⋅ ⋅  o u t p u t () 2 ) + m u () 3 ) ⋅ ⋅  o u t p u t () 3 ) + m u () 4 ) ⋅ ⋅  o u t p u t () 4 )   m u () 1 ) + m u () 2 ) + m u () 3 ) + m u () 4 )      {displaystyle {frac {cMi(1)cdot output(1)+mu(2)cdot output(2)+mu(3)cdot output(3)+mu(4)cdot output(4)}{(1)+mu(2)+mu(3)+mu(4)}}}}}}}}} {      =    () 0.3 ⋅ ⋅  0 ) + () 0.7 ⋅ ⋅  − −  0.5 ) + () 0 ⋅ ⋅  1 ) + () 0.3 ⋅ ⋅  − −  1 )   0.3 + 0.7 + 0 + 0.3      {displaystyle ={frac {(0.3cdot 0)+(0.7cdot -0.5)+(0cdot 1)+(0.3cdot -1)}{0.3+0.7+0.3}}}}      = − −  0.5   {displaystyle = 0,5} - para la salida final de control. Simple. Por supuesto, la parte difícil es averiguar qué reglas realmente funcionan correctamente en la práctica.

Si usted tiene problemas para determinar la ecuación centroide, recuerde que un centroide se define resumiendo todos los momentos (tiempos de ubicación masa) alrededor del centro de gravedad y equiparando la suma a cero. Así que si X0{displaystyle X_{0} es el centro de gravedad, Xi{displaystyle X_{i} es la ubicación de cada masa, y Mi{displaystyle M_{i} es cada masa, esto da:

     0 = ()  X  1   − −   X  0   ) ⋅ ⋅   M  1   + ()  X  2   − −   X  0   ) ⋅ ⋅   M  2   + ......  + ()  X  n   − −   X  0   ) ⋅ ⋅   M  n     {displaystyle 0=(X_{1}-X_{0})cdot M_{1}+(X_{2}-X_{0})cdot M_{2}+ldots +(X_{n}-X_{0})cdot M_{n}      0 = ()  X  1   ⋅ ⋅   M  1   +  X  2   ⋅ ⋅   M  2   + ......  +  X  n   ⋅ ⋅   M  n   ) − −   X  0   ⋅ ⋅  ()  M  1   +  M  2   + ......  +  M  n   )   {displaystyle 0=(X_{1}cdot M_{1}+X_{2}cdot M_{2}+ldots +X_{n}cdot M_{n}-X_{0}cdot (M_{1}+M_{2}+ldots +M_{n}}       X  0   ⋅ ⋅  ()  M  1   +  M  2   + ......  +  M  n   ) =  X  1   ⋅ ⋅   M  1   +  X  2   ⋅ ⋅   M  2   + ......  +  X  n   ⋅ ⋅   M  n     {displaystyle X_{0}cdot (M_{1}+M_{2}+ldots - Sí. M_{1}+X_{2}cdot M_{2}+ldots +X_{n}cdot M_{n}       X  0   =     X  1   ⋅ ⋅   M  1   +  X  2   ⋅ ⋅   M  2   + ......  +  X  n   ⋅ ⋅   M  n      M  1   +  M  2   + ......  +  M  n        {displaystyle X_{0}={frac {X_{1}cdot M_{1}+X_{2}cdot M_{2}+ldots +X_{n}cdot M_{n}{1}+M_{2}+ldots # 

En nuestro ejemplo, los valores de mu corresponden a las masas y los valores de X a la ubicación de las masas (mu, sin embargo, solo 'corresponde a las masas' si la 'masa' inicial de las funciones de salida son todas iguales/equivalentes. Si no son iguales, es decir, algunas son estrechas triángulos, mientras que otros pueden ser trapezoides anchos o triángulos con hombros, entonces se debe conocer o calcular la masa o el área de la función de salida. Es esta masa la que luego se escala por mu y se multiplica por su ubicación X_i).

Este sistema se puede implementar en un microprocesador estándar, pero ahora hay disponibles chips difusos dedicados. Por ejemplo, Adaptive Logic INC de San José, California, vende un 'chip difuso', el AL220, que puede aceptar cuatro entradas analógicas y generar cuatro salidas analógicas. A continuación se muestra un diagrama de bloques del chip:

 +--------+ +...
analog --4-- Confío análogo Silencio Silencio mux / +--4-- análogo
en la vida silenciosa
+--+----+ +...
↑
V NOVEDAD
+------------+ +--+--+
Silencio ADC / latch Silencio Silencio Silencio
+----+------+ +...
↑
Silencio
8 Y...
Silencio
Silencio
. +------------+ Silencio
+--+--+
+----+-----+ +------------+
↑
. Silencio
Silencio Silencio Silencio Silencio
+- Confeccionista +...+
Silencio (50 reglas)
+----+------+
Silencio
+----+------+
Silencioso parametros
Silencioso de la memoria
Silencio 256 x 8 Silencio
+------------+

ADC: convertidor analógico a digital
DAC: convertidor digital a digital
SH: muestre/hold

Frenos antibloqueo

Como ejemplo, considere un sistema de frenos antibloqueo, dirigido por un chip microcontrolador. El microcontrolador debe tomar decisiones en función de la temperatura del freno, la velocidad y otras variables del sistema.

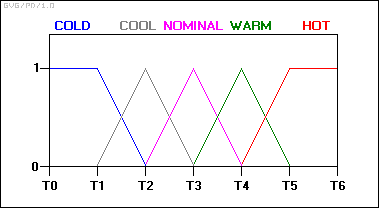
La variable "temperatura" en este sistema se puede subdividir en un rango de "estados": "frío", "frío", "moderado", " tibio, 'caliente', 'muy caliente'. La transición de un estado al siguiente es difícil de definir.

Se podría establecer un umbral estático arbitrario para dividir "tibio" de "caliente". Por ejemplo, exactamente a 90 grados, termina caliente y comienza caliente. Pero esto daría como resultado un cambio discontinuo cuando el valor de entrada supere ese umbral. La transición no sería suave, como sería necesario en situaciones de frenado.

La forma de evitar esto es hacer que los estados sean borrosos. Es decir, permitirles cambiar gradualmente de un estado a otro. Para ello, debe establecerse una relación dinámica entre diferentes factores.

Comience definiendo los estados de temperatura de entrada usando "funciones de membresía":

Con este esquema, el estado de la variable de entrada ya no salta abruptamente de un estado al siguiente. En cambio, a medida que cambia la temperatura, pierde valor en una función de membresía mientras gana valor en la siguiente. En otras palabras, su clasificación en la categoría de frío disminuye a medida que obtiene una clasificación más alta en la categoría más cálida.

En cualquier período de tiempo muestreado, el "valor de verdad" de la temperatura del freno casi siempre formará parte en algún grado de dos funciones de pertenencia: es decir, '0,6 nominal y 0,4 cálido', o '0,7 nominal y 0,3 frío', y así sucesivamente.

El ejemplo anterior demuestra una aplicación simple, usando la abstracción de valores de múltiples valores. Esto solo representa un tipo de datos, sin embargo, en este caso, la temperatura.

La adición de sofisticación adicional a este sistema de frenado podría realizarse mediante factores adicionales como la tracción, la velocidad, la inercia, configurados en funciones dinámicas, de acuerdo con el sistema difuso diseñado.

Interpretación lógica del control difuso

A pesar de la apariencia existen varias dificultades para dar una interpretación lógica rigurosa de las reglas SI-ENTONCES. Como ejemplo, interprete una regla como SI (la temperatura es "fría") ENTONCES (el calentador es "alto") por la fórmula de primer orden Fría (x)→High(y) y suponga que r es una entrada tal que Cold(r) es falso. Entonces la fórmula Cold(r)→High(t) es verdadera para cualquier t y por lo tanto cualquier t da un control correcto dado r. En el libro de Hájek (ver Capítulo 7) se da una justificación lógica rigurosa del control difuso, donde el control difuso se representa como una teoría de la lógica básica de Hájek.

En Gerla 2005 se propone otro enfoque lógico para el control difuso basado en la programación de lógica difusa: Denotar por f la función difusa que surge de un sistema de reglas SI-ENTONCES. Entonces este sistema se puede traducir a un programa borroso P que contiene una serie de reglas cuyo encabezado es "Bueno(x,y)". La interpretación de este predicado en el modelo Herbrand menos borroso de P coincide con f. Esto proporciona más herramientas útiles para el control difuso.

Simulación cualitativa difusa

Antes de que un sistema de inteligencia artificial pueda planificar la secuencia de acción, se necesita algún tipo de modelo. Para los videojuegos, el modelo es igual a las reglas del juego. Desde la perspectiva de la programación, las reglas del juego se implementan como un motor de física que acepta una acción de un jugador y calcula si la acción es válida. Después de ejecutar la acción, el juego está en estado de seguimiento. Si el objetivo no es solo jugar juegos matemáticos sino determinar las acciones para aplicaciones del mundo real, el cuello de botella más obvio es que no hay reglas de juego disponibles. El primer paso es modelar el dominio. La identificación del sistema se puede realizar con ecuaciones matemáticas precisas o con reglas difusas.

Usar lógica difusa y sistemas ANFIS (sistema de inferencia difusa basado en red adaptativa) para crear el modelo directo para un dominio tiene muchas desventajas. Una simulación cualitativa no puede determinar el estado de seguimiento correcto, pero el sistema solo adivinará qué sucederá si se tomó la acción. La simulación cualitativa Fuzzy no puede predecir los valores numéricos exactos, pero utiliza un lenguaje natural impreciso para especular sobre el futuro. Toma la situación actual más las acciones del pasado y genera el estado de seguimiento esperado del juego.

La salida del sistema ANFIS no proporciona información correcta, sino solo una notación de conjunto difuso, por ejemplo [0,0.2,0.4,0]. Después de convertir la notación establecida nuevamente en valores numéricos, la precisión empeora. Esto hace que la simulación cualitativa Fuzzy sea una mala elección para aplicaciones prácticas.

Aplicaciones

Los sistemas de control difuso son adecuados cuando la complejidad del proceso es alta, incluida la incertidumbre y el comportamiento no lineal, y no hay modelos matemáticos precisos disponibles. Se han informado aplicaciones exitosas de sistemas de control difuso en todo el mundo, principalmente en Japón, con soluciones pioneras desde los años 80.

Algunas aplicaciones reportadas en la literatura son:

• Aire acondicionado
• Sistemas de enfoque automáticos en cámaras
• Electrodomésticos (refrigeradores, lavadoras...)
• Control y optimización de procesos y sistemas industriales
• Sistemas de escritura
• Eficiencia de combustible en motores
• para el Medio Ambiente
• Sistemas de expertos
• Árboles de decisión
• Robot
• Vehículos autónomos