![{begin{aligned}y(t)&={frac {a_{0}}{2}}+sum _{k=1}^{infty }left[a_{k}cos(2pi kf_{0}t)-b_{k}sin(2pi kf_{0}t)right]\&={frac {a_{0}}{2}}+sum _{k=1}^{infty }r_{k}cos left(2pi kf_{0}t+phi _{k}right)\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/522ace082a6d8990934113a639987f09a885cf02)
![y[n],](https://wikimedia.org/api/rest_v1/media/math/render/svg/e73a8042c0d1a4c5d264982972d2ef33eda55e34)
![{begin{aligned}y[n]&=y(nT)=sum _{k=1}^{K}r_{k}(nT)cos left(2pi int _{0}^{nT}f_{k}(u) du+phi _{k}right)\&=sum _{k=1}^{K}r_{k}(nT)cos left(2pi sum _{i=1}^{n}int _{(i-1)T}^{iT}f_{k}(u) du+phi _{k}right)\&=sum _{k=1}^{K}r_{k}(nT)cos left(2pi sum _{i=1}^{n}(Tf_{k}[i])+phi _{k}right)\&=sum _{k=1}^{K}r_{k}[n]cos left({frac {2pi }{f_{mathrm {s} }}}sum _{i=1}^{n}f_{k}[i]+phi _{k}right)\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/235e423ed6dcd7564ba02d91eee3b6a012e84ce4)
![r_{k}[n]=r_{k}(nT),](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a91ccc3b0935394fad361cdc119c27a51b0c278)
![f_{k}[n]={frac {1}{T}}int _{(n-1)T}^{nT}f_{k}(t) dt,](https://wikimedia.org/api/rest_v1/media/math/render/svg/1043b3eaee212fedc8c9c8d408aad44dce3c4af1)
![y[n]=sum _{k=1}^{K}r_{k}[n]cos left(theta _{k}[n]right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbce88acb5e1e6a4ef32dd0be9bd49b78325a7de)
![{begin{aligned}theta _{k}[n]&={frac {2pi }{f_{mathrm {s} }}}sum _{i=1}^{n}f_{k}[i]+phi _{k}\&=theta _{k}[n-1]+{frac {2pi }{f_{mathrm {s} }}}f_{k}[n]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9b7b0acccac5e1f4c4d5739654caf234277411e)
![theta _{k}[0]=phi _{k}.,](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea1d7745c11e8890b24efb6c72f8c5a320d8b27e)
Instituto Americano de Estándares Nacionales
El Instituto Nacional Estadounidense de Estándares es una organización privada sin fines de lucro que supervisa el desarrollo de estándares de consenso... (leer más)
Síntesis aditiva
Ajustar Imprimir Citar
La síntesis aditiva es una técnica de síntesis de sonido que crea un timbre sumando ondas sinusoidales.
A la luz de la teoría de Fourier, se puede considerar que el timbre de los instrumentos musicales consiste en múltiples parciales armónicos o inarmónicos o sobretonos. Cada parcial es una onda sinusoidal de diferente frecuencia y amplitud que crece y decae con el tiempo debido a la modulación de una envolvente ADSR o un oscilador de baja frecuencia.
La síntesis aditiva genera sonido de manera más directa agregando la salida de múltiples generadores de onda sinusoidal. Las implementaciones alternativas pueden usar tablas de ondas precalculadas o la transformada rápida inversa de Fourier.
Explicación
Los sonidos que se escuchan en la vida cotidiana no se caracterizan por una sola frecuencia. En cambio, consisten en una suma de frecuencias sinusoidales puras, cada una con una amplitud diferente. Cuando los humanos escuchamos estas frecuencias simultáneamente, podemos reconocer el sonido. Esto es cierto tanto para "no musicales" sonidos (por ejemplo, salpicaduras de agua, hojas crujiendo, etc.) y para "sonidos musicales" (por ejemplo, una nota de piano, el canto de un pájaro, etc.). Este conjunto de parámetros (frecuencias, sus amplitudes relativas y cómo cambian las amplitudes relativas con el tiempo) están encapsulados por el timbre del sonido. El análisis de Fourier es la técnica que se utiliza para determinar estos parámetros de timbre exactos a partir de una señal de sonido general; a la inversa, el conjunto resultante de frecuencias y amplitudes se denomina serie de Fourier de la señal de sonido original.
En el caso de una nota musical, la frecuencia más baja de su timbre se designa como la frecuencia fundamental del sonido. Para simplificar, a menudo decimos que la nota se toca en esa frecuencia fundamental (por ejemplo, "do central es 261,6 Hz"), aunque el sonido de esa nota también consta de muchas otras frecuencias. El conjunto de las frecuencias restantes se denomina sobretonos (o armónicos, si sus frecuencias son múltiplos enteros de la frecuencia fundamental) del sonido. En otras palabras, la frecuencia fundamental por sí sola es responsable del tono de la nota, mientras que los sobretonos definen el timbre del sonido. Los armónicos de un piano que toca el Do central serán bastante diferentes de los armónicos de un violín que toca la misma nota; eso es lo que nos permite diferenciar los sonidos de los dos instrumentos. Incluso hay diferencias sutiles en el timbre entre diferentes versiones del mismo instrumento (por ejemplo, un piano vertical frente a un piano de cola).
La síntesis aditiva tiene como objetivo explotar esta propiedad del sonido para construir el timbre desde cero. Al sumar frecuencias puras (ondas sinusoidales) de diferentes frecuencias y amplitudes, podemos definir con precisión el timbre del sonido que queremos crear.
Definiciones
Esquema de síntesis aditiva. Las entradas a los osciladores son frecuencias fk{displaystyle f_{k} y amplitudes rk{displaystyle R_{k}.
La síntesis aditiva armónica está estrechamente relacionada con el concepto de serie de Fourier, que es una forma de expresar una función periódica como la suma de funciones sinusoidales con frecuencias iguales a múltiplos enteros de una frecuencia fundamental común. Estas sinusoides se denominan armónicos, armónicos o, en general, parciales. En general, una serie de Fourier contiene un número infinito de componentes sinusoidales, sin límite superior a la frecuencia de las funciones sinusoidales e incluye un componente de CC (uno con frecuencia de 0 Hz). Las frecuencias fuera del rango audible humano se pueden omitir en la síntesis aditiva. Como resultado, solo un número finito de términos sinusoidales con frecuencias que se encuentran dentro del rango audible se modelan en la síntesis aditiva.
Se dice que una forma de onda o función es periódica si
- Sí.()t)=Sí.()t+P){displaystyle y(t)=y(t+P)}
para todos t{displaystyle t} y durante algún período P{displaystyle P}.
La serie de Fourier de una función periódica se expresa matemáticamente como:
- Sí.()t)=a02+.. k=1JUEGO JUEGO [ak# ()2π π kf0t)− − bkpecado ()2π π kf0t)]=a02+.. k=1JUEGO JUEGO rk# ()2π π kf0t+φ φ k){displaystyle {begin{aligned}y(t) {a_{0}{2}+} ¿Por qué? kf_{0}t)-b_{k}sin(2pi kf_{0}t)right]\ {a_{0}{2}+} ¿Qué? }r_{k}cos left(2pi kf_{0}t+phi _{k}right)\end{aligned}}
dónde
- f0=1/P{displaystyle F_{0}=1/P} es la frecuencia fundamental de la onda y es igual a la recíproca del período,
- ak=rk# ()φ φ k)=2f0∫ ∫ 0PSí.()t)# ()2π π kf0t)dt,k≥ ≥ 0{displaystyle A_{k}=r_{k}cos(phi) ¿Qué? ¿Por qué? 0}
- bk=rkpecado ()φ φ k)=− − 2f0∫ ∫ 0PSí.()t)pecado ()2π π kf0t)dt,k≥ ≥ 1{displaystyle ¿Qué? - Sí. ¿Por qué? 1}
- rk=ak2+bk2{displaystyle r_{k}={sqrt {fnK}} {fn}}}}} es la amplitud de la k{displaystyle k}T armónico,
- φ φ k=atan2 ()bk,ak){displaystyle phi _{k}=operatorname {atan2} (b_{k},a_{k}} es el offset de la fase k{displaystyle k}T armónico. atan2 es la función arctangente de cuatro cuadrantes,
Ser inaudible, el componente DC, a0/2{displaystyle A_{0}/2}, y todos los componentes con frecuencias superiores a algún límite finito, Kf0{displaystyle Kf_{0}, se omiten en las siguientes expresiones de síntesis aditiva.
Forma armónica
La síntesis aditiva armónica más simple se puede expresar matemáticamente como:
- Sí.()t)=.. k=1Krk# ()2π π kf0t+φ φ k),{displaystyle y(t)=sum ¿Por qué?
()1)
Donde Sí.()t){displaystyle y(t)} es la salida de síntesis, rk{displaystyle R_{k}, kf0{displaystyle kf_{0}, y φ φ k{displaystyle phi _{k} son la amplitud, frecuencia y la fase offset, respectivamente, de la k{displaystyle k}t armónico parcial de un total de K{displaystyle K} parciales armónicos, y f0{displaystyle f_{0} es la frecuencia fundamental de la onda y la frecuencia de la nota musical.
Amplitudes dependientes del tiempo
 | Ejemplo de síntesis aditiva armónica en la que cada armónico tiene una amplitud dependiente del tiempo. La frecuencia fundamental es de 440 Hz. ¿Problemas para escuchar este archivo? Ver ayuda de medios |
Más generalmente, la amplitud de cada armónico puede ser prescrita como una función del tiempo, rk()t){displaystyle r_{k}(t)}, en cuyo caso la salida de síntesis es
- Sí.()t)=.. k=1Krk()t)# ()2π π kf0t+φ φ k){displaystyle y(t)=sum ¿Por qué?.
()2)
Cada sobre rk()t){displaystyle r_{k}(t),} debe variar lentamente en relación con el espaciamiento de frecuencia entre los sinusoides adyacentes. El ancho de banda de rk()t){displaystyle r_{k}(t)} debe ser significativamente menor que f0{displaystyle f_{0}.
Forma inarmónica
La síntesis aditiva también puede producir sonidos inarmónicos (que son formas de onda aperiódicas) en los que los armónicos individuales no necesitan tener frecuencias que sean múltiplos enteros de alguna frecuencia fundamental común. Si bien muchos instrumentos musicales convencionales tienen parciales armónicos (por ejemplo, un oboe), algunos tienen parciales inarmónicos (por ejemplo, campanas). La síntesis aditiva inarmónica se puede describir como
- Sí.()t)=.. k=1Krk()t)# ()2π π fkt+φ φ k),{displaystyle y(t)=sum ¿Por qué?
Donde fk{displaystyle f_{k} es la frecuencia constante k{displaystyle k}T parcial.
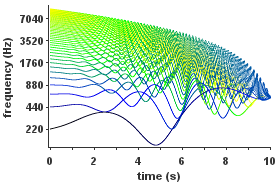 | Ejemplo de síntesis aditiva inharmónica en la que la amplitud y frecuencia de cada parcial son dependientes del tiempo. ¿Problemas para escuchar este archivo? Ver ayuda de medios |
Frecuencias dependientes del tiempo
En el caso general, la frecuencia instantánea de un sinusoide es el derivado (con respecto al tiempo) del argumento de la función sine o cosine. Si esta frecuencia está representada en hertz, en lugar de en forma de frecuencia angular, entonces este derivado se divide por 2π π {displaystyle 2pi}. Este es el caso de si el parcial es armónico o inharmónico y si su frecuencia es constante o variando tiempo.
En la forma más general, la frecuencia de cada parcial no-armónico es una función no negativa del tiempo, fk()t){displaystyle f_{k}(t)}, rendimiento
- Sí.()t)=.. k=1Krk()t)# ()2π π ∫ ∫ 0tfk()u)du+φ φ k).{displaystyle y(t)=sum ###{k=1} {K}r_{k}(t)cos left(2pi int ¿Qué?
()3)
Definiciones más amplias
Síntesis aditiva más ampliamente puede significar técnicas de síntesis de sonido que suman elementos simples para crear timbres más complejos, incluso cuando los elementos no son ondas sinusoidales. Por ejemplo, F. Richard Moore enumeró la síntesis aditiva como una de las "cuatro categorías básicas" de síntesis de sonido junto con síntesis sustractiva, síntesis no lineal y modelado físico. En este sentido amplio, los órganos de tubos, que también tienen tubos que producen formas de onda no sinusoidales, pueden considerarse como una variante de los sintetizadores aditivos. La suma de los componentes principales y las funciones de Walsh también se han clasificado como síntesis aditiva.
Métodos de implementación
Las implementaciones modernas de síntesis aditiva son principalmente digitales. (Consulte la sección Ecuaciones de tiempo discreto para conocer la teoría subyacente del tiempo discreto)
Síntesis de banco de osciladores
La síntesis aditiva se puede implementar utilizando un banco de osciladores sinusoidales, uno para cada parcial.
Síntesis de tablas de ondas
En el caso de tonos musicales armónicos cuasi periódicos, la síntesis de tabla de ondas puede ser tan general como la síntesis aditiva variable en el tiempo, pero requiere menos cálculos durante la síntesis. Como resultado, se puede lograr una implementación eficiente de la síntesis aditiva variable en el tiempo de tonos armónicos mediante el uso de síntesis de tabla de ondas.
Síntesis aditiva de grupo
La síntesis aditiva grupal es un método para agrupar parciales en grupos armónicos (que tienen diferentes frecuencias fundamentales) y sintetizar cada grupo por separado con síntesis de tabla de ondas antes de mezclar los resultados.
Síntesis FFT inversa
Se puede usar una transformada rápida de Fourier inversa para sintetizar de manera eficiente frecuencias que dividen uniformemente el período de transformación o "fotograma". Mediante una cuidadosa consideración de la representación del dominio de frecuencia DFT, también es posible sintetizar eficientemente sinusoides de frecuencias arbitrarias utilizando una serie de cuadros superpuestos y la transformada rápida inversa de Fourier.
Análisis aditivo/resíntesis
.svg)
Sinusoidal analysis/synthesis system for Sinusoidal Modeling (based on McAulay & Quatieri 1988, p. 161)
Es posible analizar los componentes de frecuencia de un sonido grabado dando una "suma de sinusoides" representación. Esta representación se puede volver a sintetizar mediante síntesis aditiva. Un método para descomponer un sonido en parciales sinusoidales que varían en el tiempo es el análisis de McAulay-Quatieri basado en la transformada de Fourier de tiempo corto (STFT).
Al modificar la representación de la suma de sinusoides, se pueden realizar alteraciones tímbricas antes de la resíntesis. Por ejemplo, un sonido armónico podría reestructurarse para que suene inarmónico y viceversa. Hibridación de sonido o "morphing" ha sido implementado por resíntesis aditiva.
El análisis/resíntesis aditivos se ha empleado en una serie de técnicas que incluyen el modelado sinusoidal, la síntesis de modelado espectral (SMS) y el modelo de sonido aditivo mejorado con ancho de banda reasignado. El software que implementa el análisis/resíntesis aditivo incluye: SPEAR, LEMUR, LORIS, SMSTools, ARSS.
Productos
Re-síntesis aditiva usando concatenación de timbre-frame:
Concatenación con crossfades (en Synclavier)
Concatenación con interpolación de sobre espectral (en Vocaloid)
New England Digital Synclavier tenía una función de resíntesis en la que las muestras podían analizarse y convertirse en ”marcos de timbres" que formaban parte de su motor de síntesis aditiva. Technos acxel, lanzado en 1987, utilizó el modelo de resíntesis/análisis aditivo, en una implementación de FFT.
También un sintetizador vocal, Vocaloid se ha implementado sobre la base de análisis/resíntesis aditivos: su modelo de voz espectral llamado Excitation plus Resonances (EpR) se amplía basándose en Spectral Modeling Synthesis (SMS), y su síntesis concatenativa de difonos se procesa usando Técnica de procesamiento de picos espectrales (SPP) similar al codificador de voz de bloqueo de fase modificado (un codificador de voz de fase mejorado para el procesamiento de formantes). Usando estas técnicas, los componentes espectrales (formantes) que consisten en parciales puramente armónicos pueden transformarse adecuadamente en la forma deseada para el modelado de sonido y la secuencia de muestras cortas (difones o fonemas) que constituyen la frase deseada, se pueden conectar sin problemas mediante la interpolación de picos de formantes y parciales coincidentes, respectivamente, en la región de transición insertada entre diferentes muestras. (Véase también Timbres dinámicos)
Aplicaciones
Instrumentos musicales
La síntesis aditiva se utiliza en instrumentos musicales electrónicos. Es la principal técnica de generación de sonido utilizada por Eminent Organs.
Síntesis de voz
En la investigación lingüística, la síntesis aditiva armónica se utilizó en la década de 1950 para reproducir espectrogramas de voz sintéticos y modificados.
Más tarde, a principios de la década de 1980, se llevaron a cabo pruebas de escucha en habla sintética sin señales acústicas para evaluar su importancia. Las frecuencias y amplitudes de los formantes variables en el tiempo derivadas de la codificación predictiva lineal se sintetizaron de forma aditiva como silbidos de tono puro. Este método se llama síntesis de onda sinusoidal. También se sabe que el modelado sinusoidal compuesto (CSM) utilizado en una función de síntesis de voz cantada en Yamaha CX5M (1984) utiliza un enfoque similar que se desarrolló de forma independiente durante 1966-1979. Estos métodos se caracterizan por la extracción y recomposición de un conjunto de picos espectrales significativos correspondientes a los diversos modos de resonancia ocurridos en la cavidad oral y la cavidad nasal, desde un punto de vista acústico. Este principio también se utilizó en un método de síntesis de modelado físico, llamado síntesis modal.
Historia
La máquina de predecir mareas de Lord Kelvin
Sintetizador armónico
Analizador armónico
El análisis armónico fue descubierto por Joseph Fourier, quien publicó un extenso tratado de su investigación en el contexto de la transferencia de calor en 1822. La teoría encontró una aplicación temprana en la predicción de mareas. Alrededor de 1876, William Thomson (más tarde ennoblecido como Lord Kelvin) construyó un predictor mecánico de mareas. Consistía en un analizador de armónicos y un sintetizador de armónicos, como se les llamaba ya en el siglo XIX. El análisis de las mediciones de mareas se realizó utilizando la máquina integradora de James Thomson. Los coeficientes de Fourier resultantes se ingresaron en el sintetizador, que luego usó un sistema de cuerdas y poleas para generar y sumar parciales sinusoidales armónicos para la predicción de futuras mareas. En 1910, se construyó una máquina similar para el análisis de formas de onda periódicas de sonido. El sintetizador dibujó un gráfico de la forma de onda de combinación, que se utilizó principalmente para la validación visual del análisis.
Resonador de Helmholtz
Tone-generator utilizándolo
Georg Ohm aplicó la teoría de Fourier al sonido en 1843. La línea de trabajo fue muy avanzada por Hermann von Helmholtz, quien publicó sus ocho años de investigación en 1863. Helmholtz creía que la percepción psicológica del color del tono es sujeto al aprendizaje, mientras que la audición en el sentido sensorial es puramente fisiológica. Apoyó la idea de que la percepción del sonido se deriva de las señales de las células nerviosas de la membrana basilar y que los apéndices elásticos de estas células vibran simpáticamente mediante tonos sinusoidales puros de frecuencias apropiadas. Helmholtz estuvo de acuerdo con el hallazgo de Ernst Chladni de 1787 de que ciertas fuentes de sonido tienen modos de vibración inarmónicos.
Analizador de sonido de Rudolph Koenig y sintetizador
sintetizador de sonido
analizador de sonido
En la época de Helmholtz, la amplificación electrónica no estaba disponible. Para la síntesis de tonos con parciales armónicos, Helmholtz construyó una serie de diapasones excitados eléctricamente y cámaras de resonancia acústica que permitían el ajuste de las amplitudes de los parciales. Construidos al menos en 1862, estos fueron a su vez refinados por Rudolph Koenig, quien demostró su propia configuración en 1872. Para la síntesis armónica, Koenig también construyó un gran aparato basado en su sirena de onda. Era neumático y utilizaba ruedas tonales recortadas, y fue criticado por la baja pureza de sus tonos parciales. También los tubos de tibia de los órganos de tubos tienen formas de onda casi sinusoidales y se pueden combinar en forma de síntesis aditiva.
En 1938, con nueva e importante evidencia de apoyo, se informó en las páginas de Popular Science Monthly que las cuerdas vocales humanas funcionan como una sirena de incendios para producir un tono rico en armónicos, que luego es filtrado por el tracto vocal para producir diferentes tonos de vocales. En ese momento, el órgano Hammond aditivo ya estaba en el mercado. La mayoría de los primeros fabricantes de órganos electrónicos pensaron que era demasiado costoso fabricar la pluralidad de osciladores requeridos por los órganos aditivos y, en cambio, comenzaron a construir los sustractivos. En una reunión del Instituto de Ingenieros de Radio de 1940, el ingeniero jefe de campo de Hammond explicó que el nuevo Novachord de la compañía tenía un "sistema sustractivo" en contraste con el órgano Hammond original en el que "los tonos finales se construyeron combinando ondas de sonido". Alan Douglas usó los calificativos aditivo y sustractivo para describir diferentes tipos de órganos electrónicos en un artículo de 1948 presentado a la Royal Musical Association. La redacción contemporánea síntesis aditiva y síntesis sustractiva se puede encontrar en su libro de 1957 La producción eléctrica de la música, en el que enumera categóricamente tres métodos de formación de tonos-colores musicales, en los apartados titulados Síntesis aditiva, Síntesis sustractiva, y Otras formas de combinación.
Un sintetizador aditivo moderno típico produce su salida como una señal analógica eléctrica o como audio digital, como en el caso de los sintetizadores de software, que se hicieron populares alrededor del año 2000.
Cronología
La siguiente es una cronología de sintetizadores y dispositivos analógicos y digitales destacados histórica y tecnológicamente que implementan la síntesis aditiva.
| Aplicación o publicación de investigaciones | Disponible comercialmente | Empresa o institución | Sintetizador o dispositivo de síntesis | Descripción | Muestras de audio |
|---|---|---|---|---|---|
| 1900 | 1906 | New England Electric Music Company | Telharmonium | El primer sintetizador de música polifónico y sensible al tacto. Ejecutado síntesis aditiva sinuosoidal utilizando tonewheels y alternadores. Invenido por Thaddeus Cahill. | no grabaciones conocidas |
| 1933 | 1935 | Hammond Organ Company | Hammond Organ | Un sintetizador aditivo electrónico que fue comercialmente más exitoso que Telharmonium. Ejecutado síntesis aditiva sinusoidal usando tonewheels y pastillas magnéticas. Inventada por Laurens Hammond. |  Modelo A(help·info) |
| 1950 o antes | Haskins Laboratories | Pattern Playback | Un sistema de síntesis de discursos que controlaba las amplitudes de las parciales armónicas por un espectrograma que fue dibujado a mano o un resultado de análisis. Las parciales fueron generadas por un tonewheel óptico de múltiples vías. | muestras | |
| 1958 | ANS | Un sintetizador aditivo que jugó puntuaciones como espectrograma microtonal usando múltiples tonewheels ópticos multipista. Invenido por Evgeny Murzin. Un instrumento similar que utilizó osciladores electrónicos, el Osciltor Bank, y su dispositivo de entrada Espectrograma fueron realizados por Hugh Le Caine en 1959. | 1964 modelo(help·info) | ||
| 1963 | MIT | Un sistema fuera de línea para el análisis espectral digital y la síntesis del ataque y partes estables de instrumentos musicales timbres por David Luce. | |||
| 1964 | University of Illinois | Armonic Tone Generator | Un sistema de síntesis aditivo electrónico y armónico inventado por James Beauchamp. | muestras (info) | |
| 1974 o antes | 1974 | RMI | Sintetizador Armónico | El primer producto sintetizador que implementó síntesis aditiva utilizando osciladores digitales. El sintetizador también tenía un filtro analógico que cudía tiempo. RMI era una subsidiaria de Allen Organ Company, que había lanzado el primer órgano comercial de la iglesia digital, el Allen Computer Organ, en 1971, utilizando tecnología digital desarrollada por North American Rockwell. | 1 2 3 4 |
| 1974 | EMS (Londres) | Oscilador digital Banco | Banco de osciladores digitales con formas de onda arbitrarias, controles individuales de frecuencia y amplitud, destinados a utilizar en análisis-resíntesis con la digital Analysing Filter Bank (AFB) también construido en EMS. También conocido como: DOB. | en el nuevo sonido de la música | |
| 1976 | 1976 | Fairlight | Qasar M8 | Un sintetizador todo digital que utilizó la rápida transformación de Fourier para crear muestras de envolturas de amplitud dibujadas interactivamente de armónicos. | muestras |
| 1977 | Bell Labs | Sintetizador digital | Un sintetizador aditivo digital en tiempo real que ha sido llamado el primer sintetizador digital verdadero. También conocido como: Alles Machine, Alice. | muestra (info) | |
| 1979 | 1979 | New England Digital | Synclavier II | Un sintetizador digital comercial que permitió el desarrollo de timbre a lo largo del tiempo mediante movimientos cruzados suaves entre ondas generadas por síntesis aditiva. | Jon Appleton - Sashasonjon(help·info) |
Ecuaciones de tiempo discreto
En las implementaciones digitales de síntesis aditiva, se utilizan ecuaciones discretas en lugar de las ecuaciones de síntesis de tiempo continuo. Una convención notacional para señales discretas utiliza soportes, es decir. Sí.[n]{displaystyle y[n],} y el argumento n{displaystyle n,} puede ser valores enteros. Si la salida de síntesis de tiempo continuo Sí.()t){displaystyle y(t),} se espera que esté suficientemente limitado; por debajo de la mitad de la tasa de muestreo o fs/2{displaystyle f_{mathrm}/2,}, basta probar directamente la expresión de tiempo continuo para obtener la ecuación discreta de síntesis. La salida de síntesis continua puede ser reconstruida posteriormente a partir de las muestras utilizando un convertidor digital-a-analógico. El período de muestreo es T=1/fs{displaystyle T=1/f_{mathrm {s},}.
Empezando con (3),
- Sí.()t)=.. k=1Krk()t)# ()2π π ∫ ∫ 0tfk()u)du+φ φ k){displaystyle y(t)=sum ###{k=1} {K}r_{k}(t)cos left(2pi int ¿Por qué?
y muestreo en tiempos discretos t=nT=n/fs{displaystyle t=nT=n/f_{mathrm {s},} resultados en
- Sí.[n]=Sí.()nT)=.. k=1Krk()nT)# ()2π π ∫ ∫ 0nTfk()u)du+φ φ k)=.. k=1Krk()nT)# ()2π π .. i=1n∫ ∫ ()i− − 1)TiTfk()u)du+φ φ k)=.. k=1Krk()nT)# ()2π π .. i=1n()Tfk[i])+φ φ k)=.. k=1Krk[n]# ()2π π fs.. i=1nfk[i]+φ φ k){displaystyle {begin{aligned}y[n] _{k=1} {K}r_{k}(nT)cos left(2pi int ¿Qué? du+phi ¿Por qué? ¿Por qué? du+phi ¿Por qué? _{k=1} {K}r_{k}(nT)cos left(2pi sum ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ }{f_{mathrm { s}}sum ¿Por qué?
dónde
- rk[n]=rk()nT){displaystyle [n]=r_{k}(nT),} es el sobre de amplitud variable de tiempo discreto
- fk[n]=1T∫ ∫ ()n− − 1)TnTfk()t)dt{displaystyle f_{k}[n]={frac {1}{T}int _{(n-1)T}{nT}f_{k}(t) dt,} es la diferencia discreta-time atrasada frecuencia instantánea.
Esto es equivalente a
- Sí.[n]=.. k=1Krk[n]# ()Silencio Silencio k[n]){displaystyle y[n]=sum ¿Por qué?
dónde
- Silencio Silencio k[n]=2π π fs.. i=1nfk[i]+φ φ k=Silencio Silencio k[n− − 1]+2π π fsfk[n]{displaystyle {begin{aligned}theta _{k}[n] }{f_{mathrm { s}}sum ¿Por qué? ¿Qué? {f} {f} {f} {f}}\\f}}}}} para todos 0,}" xmlns="http://www.w3.org/1998/Math/MathML">n■0{displaystyle n título0,}
0," aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/947e5ee625b999ff1849997c89a25281e60d2240" style="vertical-align: -0.338ex; width:6.043ex; height:2.176ex;"/>
y
- Silencio Silencio k[0]=φ φ k.{displaystyle theta _{k}[0]=phi _{k}
- Te puede interesar
- Te puede interesar
Berlín (banda)
Berlin es una banda estadounidense de new wave formada en Los Ángeles en 1978. La banda obtuvo éxito comercial en la década de 1980 con sencillos como... (leer más)
- Te puede interesar
Composicion musical
Composición musical puede referirse a una pieza original u obra musical, ya sea vocal o instrumental, la estructura de una pieza musical o el proceso de... (leer más)
Más resultados...