Simulación de accidente
Una simulación de choque es una recreación virtual de una prueba de choque destructiva de un automóvil o un sistema de barandillas de carretera utilizando una simulación por computadora para examinar el nivel de seguridad del automóvil y sus ocupantes. Los fabricantes de automóviles utilizan simulaciones de accidentes durante el análisis de ingeniería asistida por computadora (CAE) para determinar la resistencia a los accidentes en el proceso de diseño asistido por computadora (CAD) de modelado de automóviles nuevos. Durante una simulación de accidente, la energía cinética, o energía de movimiento, que tiene un vehículo antes del impacto se transforma en energía de deformación, principalmente por deformación plástica (plasticidad) del material de la carrocería (Body in White), al final del impacto.
Los datos obtenidos de una simulación de accidente indican la capacidad de la carrocería del automóvil o de la estructura de la barandilla para proteger a los ocupantes del vehículo durante una colisión (y también a los peatones atropellados por un automóvil) contra lesiones. Los resultados importantes son las deformaciones (por ejemplo, intrusiones del volante) del espacio de los ocupantes (conductor, pasajeros) y las desaceleraciones (por ejemplo, aceleración de la cabeza) que sienten, que deben caer por debajo de los valores umbral fijados por las normas legales de seguridad para automóviles. Para modelar pruebas de choque reales, las simulaciones de choques actuales incluyen modelos virtuales de maniquíes de pruebas de choque y de dispositivos de seguridad pasiva (cinturones de seguridad, airbags, tableros de instrumentos amortiguadores, etc.). Las pruebas del riel guía evalúan la desaceleración del vehículo y el potencial de vuelco, así como la penetración de la barrera por parte de los vehículos.
Historia
En los años 1970 se intentó simular accidentes automovilísticos con sistemas de masa-resorte no lineales después de la calibración, lo que requería como entrada los resultados de pruebas físicas destructivas de laboratorio, necesarias para determinar el comportamiento mecánico de aplastamiento de cada componente del resorte de el sistema modelado. "Primer principio" Sin embargo, las simulaciones como modelos de elementos finitos más elaborados solo necesitan la definición de la geometría estructural y las propiedades básicas del material (reología del acero de la carrocería, vidrio, piezas de plástico, etc.) como entrada para generar el modelo numérico.
Los orígenes de la simulación industrial computarizada de accidentes automovilísticos de primer principio se encuentran en aplicaciones de defensa militar, espacio exterior y plantas de energía nuclear civiles. Tras la presentación por parte del Grupo ESI de una simulación del accidente accidental de un avión de combate militar contra una central nuclear el 30 de mayo de 1978, en una reunión organizada por la Verein Deutscher Ingenieure (VDI) en Stuttgart, los fabricantes de automóviles fueron alertados sobre la posibilidad de utilizar esta tecnología para la simulación de pruebas destructivas de accidentes automovilísticos (Haug 1981).
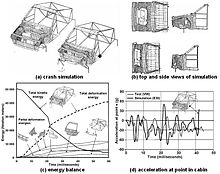
En los años siguientes, los fabricantes de automóviles alemanes produjeron estudios de simulación de accidentes más complejos, simulando el comportamiento en caso de choque de componentes individuales de la carrocería, conjuntos de componentes y carrocerías de un cuarto y media carrocería en blanco (BIW). Estos experimentos culminaron en un proyecto conjunto de la Forschungsgemeinschaft Automobil-Technik (FAT), un conglomerado de los siete fabricantes de automóviles alemanes (Audi, BMW, Ford, Mercedes-Benz, Opel, Porsche y Volkswagen), que probó la aplicabilidad de dos códigos emergentes de simulación de accidentes comerciales. Estos códigos de simulación recrearon un impacto frontal de la estructura completa de un automóvil de pasajeros (Haug 1986) y se ejecutaron hasta su finalización en una computadora durante la noche. Ahora que el tiempo de respuesta entre dos envíos de trabajos consecutivos (ejecuciones por computadora) no excedía un día, los ingenieros pudieron comprender mejor el comportamiento del choque y realizar mejoras eficientes y progresivas en la estructura de la carrocería del automóvil analizada. El software de ingeniería asistida por ordenador (CAE) se ha convertido últimamente en una norma en la simulación de pruebas de choque. La combinación de herramientas de aprendizaje automático y CAE permitió una aceleración mucho mejor del software de simulación. Los ingenieros utilizaron ML para predecir:
- La aceleración del pecho muñeco
- El desplazamiento hacia delante del muñeco
- La aceleración máxima del pecho y el criterio de lesión en la cabeza.
Aplicación
Las simulaciones de choques se utilizan para investigar la seguridad de los ocupantes del automóvil durante los impactos en la estructura frontal del automóvil en una "colisión frontal" o "impacto frontal", la estructura lateral del automóvil en una “colisión lateral” o “impacto lateral”, la estructura trasera de un automóvil en una "colisión trasera" o “impacto trasero”, y la estructura del techo del automóvil cuando éste vuelca durante un "vuelco". Las simulaciones de accidentes también se pueden utilizar para evaluar las lesiones sufridas por los peatones atropellados por un coche.
Beneficios
Una simulación de accidente produce resultados sin pruebas destructivas reales de un nuevo modelo de automóvil. De esta forma, se pueden realizar pruebas de forma rápida y económica en un ordenador, lo que permite optimizar el diseño antes de que se haya fabricado un prototipo real del coche. Mediante una simulación, se pueden resolver problemas antes de gastar tiempo y dinero en una prueba de choque real. La gran flexibilidad de la salida impresa y la visualización gráfica permite a los diseñadores resolver algunos problemas que habrían sido casi imposibles sin la ayuda de una computadora.
Análisis
Un gran número de simulaciones de accidentes utilizan un método de análisis llamado método de elementos finitos. Los problemas complejos se resuelven dividiendo una superficie en un número grande pero finito de elementos y determinando el movimiento de estos elementos durante períodos de tiempo muy pequeños. Otro enfoque para las simulaciones de accidentes se realiza mediante la aplicación del método de elementos macro. La diferencia entre las dos metodologías mencionadas anteriormente es que la estructura en el caso del método de elementos macro consta de un número menor de elementos. El algoritmo de cálculo de la deformación de la estructura se basa en datos experimentales en lugar de calcularse a partir de ecuaciones diferenciales parciales.
Pam-Crash inició la simulación de accidentes y, junto con LS-DYNA, es un paquete de software que se utiliza ampliamente para la aplicación del método de elementos finitos. Este método permite el modelado detallado de una estructura, pero la desventaja radica en los altos requisitos de unidades de procesamiento y el tiempo de cálculo. Visual Crash Studio utiliza la metodología de elementos macro. En comparación con FEM, tiene algunas limitaciones de modelado y condiciones de contorno, pero su aplicación no requiere computadoras avanzadas y el tiempo de cálculo es incomparablemente menor. Los dos métodos presentados se complementan. El método de elementos macro es útil en las primeras etapas del proceso de diseño de estructuras, mientras que el método de elementos finitos funciona bien en sus etapas finales.
Análisis estructural
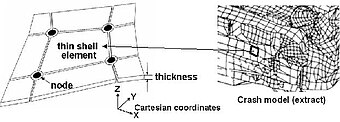
En una simulación de accidente típica, la estructura de la carrocería del automóvil se analiza mediante discretización espacial, es decir, dividiendo el movimiento continuo de la carrocería en tiempo real en cambios más pequeños de posición en pasos de tiempo pequeños y discretos. La discretización implica subdividir la superficie de las piezas delgadas de chapa metálica que las componen en un gran número (cerca de un millón en 2006) de regiones cuadriláteras o triangulares, cada una de las cuales abarca el área entre los "nodos" y las superficies de los nodos. al que se fijan sus esquinas. Cada elemento tiene masa, que se distribuye como masas concentradas y como momentos de inercia de masa a sus nodos de conexión. Cada nodo tiene 6 grados de libertad cinemáticos, es decir, un nodo puede moverse en tres direcciones lineales bajo traslación y puede girar alrededor de tres ejes independientes. Las coordenadas espaciales (x), desplazamiento (u), velocidad (v) y aceleración (a) de cada nodo se expresa principalmente en un sistema de coordenadas cartesianas rectangular tridimensional con ejes X, Y y Z.
Si los nodos se mueven durante una simulación de choque, los elementos conectados se mueven, se estiran y se doblan con sus nodos, lo que hace que impartan fuerzas y momentos a sus conexiones nodales. Las fuerzas y momentos en los nodos corresponden a las fuerzas y momentos de inercia, causados por sus aceleraciones traslacionales (lineales) y angulares y a las fuerzas y momentos transmitidos por la resistencia del material estructural de los elementos conectados a medida que se deforman. A veces, se aplican cargas estructurales externas adicionales, como cargas de gravedad provenientes del peso propio de las piezas o cargas agregadas de masas externas.
Las fuerzas y momentos de todos los nodos se recogen en un vector de columna (o matriz de columna), y las ecuaciones de movimiento dependientes del tiempo (en equilibrio dinámico) se pueden escribir de la siguiente manera.
donde vector (máximo vector de aceleración) recoge las fuerzas inercias en los nodos, recoge las cargas nodal externas, y recoge las fuerzas de resistencia internas de la deformación del material. M es una matriz diagonal de las masas nodal. Cada vector (u, v, a, F, etc.) tiene dimensión 6 veces el número total de nodos en el modelo de choque (alrededor de 6 millones de “grados de libertad” por cada 1 millón de "nodos" en los modelos de elementos finitos de cáscara delgada 3-D).
Análisis de tiempo
Una simulación de accidente también utiliza la discretización del tiempo para separar los cambios continuos en el tiempo en segmentos muy pequeños y utilizables. Las ecuaciones dinámicas de movimiento se mantienen en todo momento durante una simulación de choque y deben integrarse en el tiempo, t, a partir de una condición inicial en el tiempo cero, que es justo antes del choque. Según el método explícito de integración de tiempo de diferencias finitas utilizado por la mayoría de los códigos de accidentes, las aceleraciones, velocidades y desplazamientos del cuerpo están relacionados mediante las siguientes ecuaciones.
En estas ecuaciones los subscriptos n±1/2, n, n+1 denota tiempos pasados, presentes y futuros, t, a mitad y intervalos de tiempo completo con pasos de tiempo y , respectivamente.
Solución
El sistema anterior de ecuaciones lineales se resuelve para las aceleraciones, Las velocidades, y los desplazamientos, , en cada punto discreto en el tiempo, t, durante la duración del accidente. Esta solución es trivial, ya que la matriz de masa es diagonal. El tiempo de la computadora es proporcional al número de elementos finitos y el número de pasos de tiempo de solución. El paso del tiempo de solución estable, , se limita a la estabilidad numérica, como se expresa en la condición Courant-Friedrichs-Lewy (CFL), en la que se afirma que “en cualquier simulación computarizada del tiempo, el paso del tiempo debe ser inferior al tiempo para que ocurra alguna acción significativa, y preferiblemente menos”. En una simulación de choque, las acciones más importantes son las señales acústicas que viajan dentro del material estructural.
La velocidad de la onda de tensión elástica sólida asciende a
Donde es el módulo elástico inicial (antes de la deformación plástica) del material y es la densidad de masa. Por lo tanto, el mayor paso de tiempo estable para un material dado es
- ,
Donde es la distancia más pequeña entre los dos nodos del modelo numérico de simulación de choque.
Dado que esta distancia puede cambiar durante una simulación, el paso de tiempo estable cambia y debe actualizarse continuamente a medida que la solución avanza en el tiempo. Cuando se utiliza acero, el valor típico del paso de tiempo estable es de aproximadamente un microsegundo cuando la distancia de nodo discreto más pequeña en la malla del modelo de elementos finitos es de aproximadamente 5 milímetros. Se necesitan entonces más de 100.000 intervalos de tiempo para resolver un accidente que dura una décima de segundo. Esta cifra se supera en muchos modelos de accidentes industriales que exigen solucionadores de accidentes optimizados con funciones de informática de alto rendimiento (HPC), como vectorización y computación paralela.
Véase también
- Método de elementos finitos en la mecánica estructural
- Análisis de elementos finitos
- Prueba de choque
Referencias
- ^ Belaid, Mohamed Karim; Rabus, Maximilian; Krestel, Ralf (1 de julio de 2021). "CrashNet: una arquitectura encoder-decoder para predecir los resultados de la prueba de fallos". Data Mining and Knowledge Discovery. 35 (4): 1688-1709. doi:10.1007/s10618-021-00761-9. ISSN 1573-756X.
- ^ Rabus, Maximilian; Belaid, Mohamed Karim; Maurer, Simon Alexander; Hiermaier, Stefan (23 de junio de 2022). "Desarrollo de un modelo para la predicción de cargas ocupantes en accidentes de vehículos: introducción del Críter de Carga de Ocupación Real para Predicción (ROLC$_p$)". Tecnología Automotriz y Motor. 7 (3–4): 229–244. doi:10.1007/s41104-022-00111-x. ISSN 2365-5135. S2CID 249996973.
- ^ Lim, Jae Moon (1 de junio de 2021). "Un método para predecir HIC15, Chest G's y Chest Deflection basado en los resultados de las pruebas de impacto frontal de USNCAP". International Journal of Automotive Technology. 22 (3): 657–663. doi:10.1007/s12239-021-0061-z. ISSN 1976-3832. S2CID 236395205.
- Haug, E. (1981) "Iniciar el análisis de seguridad mediante experimentos numéricos destructivos", EUROMECH 121, Academia Polaca de Ciencias, Operaciones de Ingeniería 29(1), 39–49.
- Haug, E., T. Scharnhorst, P. Du Bois (1986) "FEM-Crash, Berechnung eines Fahrzeugfrontalaufpralls", VDI Berichte 613, 479–505.

















