Símplex

Los cuatro sencillos que se pueden representar plenamente en el espacio 3D.

En geometría, un simple (plural: simples o simples) es una generalización de la noción de un triángulo o tetraedro a dimensiones arbitrarias. El simplex se llama así porque representa el politopo más simple posible en cualquier dimensión dada. Por ejemplo,

• un simplex 0-dimensional es un punto,
• a 1-dimensional simplex es un segmento de línea,
• a 2-dimensional simplex es un triángulo,
• un simplex tridimensional es un tetraedro, y
• un simplex 4-dimensional es un 5-cel.

Específicamente, a k-simplex es un k- politopa dimensional que es el casco convexo de su k+ 1 vértices. Más formalmente, suponga el k+ 1 puntos u0,...... ,uk▪ ▪ Rk{displaystyle u_{0},dotsu_{k}in mathbb {R} ^{k} son afinadamente independientes, lo que significa u1− − u0,...... ,uk− − u0{displaystyle ¿Qué? son linealmente independientes. Entonces, el simplex determinado por ellos es el conjunto de puntos

C={}Silencio Silencio 0u0+⋯ ⋯ +Silencio Silencio kukSilencio.. i=0kSilencio Silencio i=1ySilencio Silencio i≥ ≥ 0parai=0,...... ,k}{displaystyle C=lefttheta ¿Qué? + 'theta ¿Qué? Bigg, ¿qué tal? - ¿Por qué?

Esta representación en términos de vértices ponderados se conoce como sistema de coordenadas baricéntrico.

Un símplex regular es un símplex que también es un politopo regular. Un k-símplex regular se puede construir a partir de un (k − 1)-simplex regular conectando un nuevo vértice a todos los vértices originales por la longitud de la arista común.

El símplex estándar o símplex de probabilidad es el símplex k - 1 dimensional cuyos vértices son el estándar k vectores unitarios, o

{}x▪ ▪ Rk:x0+⋯ ⋯ +xk− − 1=1,xi≥ ≥ 0parai=0,...... ,k− − 1}.{displaystyle left{xin mathbb [R] ^{k}:x_{0}+dots +x_{k-1}=1,x_{i}geq 0{text{ for }i=0,dotsk-1right}

En topología y combinatoria, es común "pegar juntos" simples para formar un complejo simplicial. La estructura combinatoria asociada se denomina complejo simplicio abstracto, en cuyo contexto la palabra "simple" simplemente significa cualquier conjunto finito de vértices.

Historia

El concepto de símplex lo conocía William Kingdon Clifford, quien escribió sobre estas formas en 1886 pero las llamó "confines principales". Henri Poincaré, al escribir sobre topología algebraica en 1900, los llamó "tetraedros generalizados". En 1902, Pieter Hendrik Schoute describió el concepto primero con el superlativo latino simplicissimum ("simplest") y luego con el mismo adjetivo latino en la forma normal simplex ("sencillo").

La familia simplex regular es la primera de tres familias de politopos regulares, etiquetadas por Donald Coxeter como α_n, siendo las otras dos las familia de politopos cruzados, etiquetada como β_n, y los hipercubos, etiquetados como γ_n. Una cuarta familia, la teselación del espacio n-dimensional por infinitos hipercubos, la etiquetó como δ_n.

Elementos

El casco convexo de cualquier subconjunto no vacío del n+ 1 puntos que definen un n- El complejo se llama cara del simplex. Los rostros son simplices. En particular, el casco convexo de un subconjunto de tamaño m+ 1 (del n+ 1 puntos de definición) es un m-simplex, llamado un m- Cara de la n-simplex. Los 0-caras (es decir, los puntos definidos como conjuntos de tamaño 1) se llaman los vertices (singular: vértice), los 1-caras se llaman el bordes, eln− 1)-caras se llaman facetas, y la suela n- La cara es toda n- Simplex en sí. En general, el número de m-caras es igual al coeficiente binomio ()n+1m+1){displaystyle {tbinom} {n+1}{m+1}}. En consecuencia, el número de m-caras de un n-simplex se puede encontrar en la columna (m+ 1) de fila (n+ 1) del triángulo de Pascal. Un simplex A es un coface de un simplex B si B es una cara de A. Cara y faceta puede tener diferentes significados al describir tipos de simplices en un complejo simplicial; ver complejo simplical para más detalle.

El número de caras 1 (aristas) del n-simple es el número del triángulo n-ésimo, el número de caras 2 del n-simple es el (n − 1) número de tetraedro, el número de 3 caras del n-simple es el (n − 2) número de 5 celdas, y así sucesivamente.

n- Elementos simples

Δn	Nombre	Schläfli Coxeter	0- caras (vicios)	1- caras (edges)	2- caras (caras)	3- caras (células)	4- caras	5- caras	6- caras	7- caras	8- caras	9- caras	10- caras	Sum = 2n+ 1− 1
Δ0	0-simple (punto)	()	1											1
Δ1	1-simple (sección de línea)	{ } = () ∨ () = 2 ⋅ ()	2	1										3
Δ2	2-simple (triángulo)	{3} = 3 ⋅ ()	3	3	1									7
Δ3	3-simple (tetraedro)	{3,3} = 4 ⋅ ()	4	6	4	1								15
Δ4	4-simple (5 celdas)	{3}3} = 5 ⋅ ()	5	10	10	5	1							31
Δ5	5-simplex	{3}4} = 6 ⋅ ()	6	15	20	15	6	1						63
Δ6	6-simplex	{3}5} = 7 ⋅ ()	7	21	35	35	21	7	1					127
Δ7	7-simplex	{3}6} = 8 ⋅ ()	8	28	56	70	56	28	8	1				255
Δ8	8-simplex	{3}7} = 9 ⋅ ()	9	36	84	126	126	84	36	9	1			511
Δ9	9-simplex	{3}8} = 10 ⋅ ()	10	45	120	210	252	210	120	45	10	1		1023
Δ10	10-simplex	{3}9} = 11 ⋅ ()	11	55	165	330	462	462	330	165	55	11	1	2047

En términos sencillos, un n-simplex es una forma simple (un polígono) que requiere n dimensiones. Considere un segmento de línea AB como una "forma" en un espacio unidimensional (el espacio unidimensional es la línea en la que se encuentra el segmento). Se puede colocar un nuevo punto C en algún lugar fuera de la línea. La nueva forma, triángulo ABC, requiere dos dimensiones; no puede caber en el espacio unidimensional original. El triángulo es el 2-simplex, una forma simple que requiere dos dimensiones. Considere un triángulo ABC, una forma en un espacio bidimensional (el plano en el que reside el triángulo). Se puede colocar un nuevo punto D en algún lugar fuera del plano. La nueva forma, tetraedro ABCD, requiere tres dimensiones; no puede caber en el espacio bidimensional original. El tetraedro es el 3-simplex, una forma simple que requiere tres dimensiones. Considere el tetraedro ABCD, una forma en un espacio tridimensional (el espacio tridimensional en el que se encuentra el tetraedro). Se puede colocar un nuevo punto E en algún lugar fuera del espacio tridimensional. La nueva forma ABCDE, llamada 5 celdas, requiere cuatro dimensiones y se llama 4-simplex; no puede caber en el espacio tridimensional original. (Tampoco se puede visualizar fácilmente). Esta idea se puede generalizar, es decir, agregar un solo punto nuevo fuera del espacio ocupado actualmente, lo que requiere ir a la siguiente dimensión superior para mantener la nueva forma. Esta idea también se puede trabajar al revés: el segmento de línea con el que comenzamos es una forma simple que requiere un espacio unidimensional para contenerlo; el segmento de línea es el 1-simplex. El segmento de línea en sí se formó comenzando con un solo punto en el espacio de 0 dimensiones (este punto inicial es el 0-simple) y agregando un segundo punto, lo que requirió el aumento al espacio de 1 dimensión.

Más formalmente, un (n + 1)-simple se puede construir como una unión (operador ∨) de un n-simple y un punto, (). Un (m + n + 1)-simple se puede construir como una unión de un m-simple y un n-simple. Los dos simples están orientados para ser completamente normales entre sí, con traslación en una dirección ortogonal a ambos. Un 1-simplex es la unión de dos puntos: () ∨ () = 2 ⋅ (). Un 2-simplex general (triángulo escaleno) es la unión de tres puntos: () ∨ () ∨ (). Un triángulo isósceles es la unión de un 1-simple y un punto: { } ∨ (). Un triángulo equilátero es 3 ⋅ () o {3}. Un 3-simplex general es la unión de 4 puntos: () ∨ () ∨ () ∨ (). Un 3-simplex con simetría especular se puede expresar como la unión de una arista y dos puntos: { } ∨ () ∨ (). Un 3-simplex con simetría triangular se puede expresar como la unión de un triángulo equilátero y 1 punto: 3.()∨() o {3}∨(). Un tetraedro regular es 4 ⋅ () o {3,3} y así sucesivamente.

Los números de caras en la tabla anterior son los mismos que en el triángulo de Pascal, sin la diagonal izquierda.

El número total de caras es siempre un poder de dos menos uno. Esta figura (una proyección del tesseract) muestra los centroides de las 15 caras del tetraedro.

En algunas convenciones, el conjunto vacío se define como un (−1)-simple. La definición del símplex anterior todavía tiene sentido si n = −1. Esta convención es más común en aplicaciones a la topología algebraica (como la homología simplicial) que al estudio de politopos.

Gráficas simétricas de simples regulares

Estos polígonos de Petrie (proyecciones ortogonales sesgadas) muestran todos los vértices del símplex regular en un círculo y todos los pares de vértices conectados por aristas.

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20

El símplex estándar

El estándar 2-simplex dentro R³

El estándar n-simple (o unidad n-simple) es el subconjunto de Rⁿ⁺¹ dado por

Δ Δ n={}()t0,...... ,tn)▪ ▪ Rn+1Silencio.. i=0nti=1yti≥ ≥ 0parai=0,...... ,n}{displaystyle Delta ^{n}=left{(t_{0},dotst_{n}in mathbb {R} {fn}~ {fn}} {fn}} {fn}} {fn} {cH00}}}} {fn}}} {fn}}} {fn}} {fn}}}} {\\fn}}}}}}\\\fn}}}}\\\\\\\\\\\\\\\\\\fn}\\\\\\\\\\\\fn}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} Bigg. ¿Por qué?

El simplex Δⁿ se encuentra en el hiperplano afín obtenido al eliminar la restricción t_i ≥ 0 en la definición anterior.

Los n + 1 vértices del estándar n-simplex son los puntos e_i ∈ Rⁿ⁺¹, donde

e₀ = (1, 0, 0,..., 0),

e₁ = (0, 1, 0,..., 0),

⋮

e_n = (0, 0, 0,..., 1).

Hay un mapa canónico desde el estándar n-simple hasta un arbitrario n-simple con vértices (v₀,..., v_n) dado por

()t0,...... ,tn)↦ ↦ .. i=0ntivi{displaystyle (t_{0},ldotst_{n}mapsto sum ¿Qué?

Los coeficientes t_i se denominan coordenadas baricéntricas de un punto en el n-simple. Tal símplex general a menudo se denomina afín n-simplex, para enfatizar que el mapa canónico es una transformación afín. A veces también se denomina orientado afín n-simplex para enfatizar que el mapa canónico puede conservar o invertir la orientación.

Más generalmente, hay un mapa canónico desde el estándar ()n− − 1){displaystyle (n-1)}-simplex (con n vertices) sobre cualquier politopo con n vértices, dados por la misma ecuación (indización modificadora):

()t1,...... ,tn)↦ ↦ .. i=1ntivi{displaystyle (t_{1},ldotst_{n}mapsto sum ¿Qué?

Estas son conocidas como coordenadas barícentricas generalizadas, y expresan cada politopo como el imagen de un simplex: Δ Δ n− − 1↠ ↠ P.{displaystyle Delta ^{n-1}twoheadrightarrow P.}

Una función comúnmente utilizada Rⁿ al interior del estándar ()n− − 1){displaystyle (n-1)}-simplex es la función softmax, o función exponencial normalizada; esto generaliza la función logística estándar.

Ejemplos

• Δ⁰ es el punto 1 en R¹.
• Δ¹ es el segmento de línea (1, 0) y (0, 1) en R².
• Δ² es el triángulo equilátero con vértices (1, 0, 0), (0, 1, 0) y (0, 0, 1) en R³.
• Δ³ es el tetraedro regular con vértices (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0) y (0, 0, 0, 1) en R⁴.
• Δ⁴ es la 5 celdas regulares con vértices (1, 0, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0, 0), (0, 0, 0, 1, 0) y (0, 0, 0, 0, 1) en R⁵.

Coordenadas crecientes

Se obtiene un sistema de coordenadas alternativo tomando la suma indefinida:

s0=0s1=s0+t0=t0s2=s1+t1=t0+t1s3=s2+t2=t0+t1+t2⋮ ⋮ sn=sn− − 1+tn− − 1=t0+t1+⋯ ⋯ +tn− − 1sn+1=sn+tn=t0+t1+⋯ ⋯ +tn=1{fnMicrosoft Sans {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {0}=t_{0}=t_{0}s_{2}=s_{1}+t_}=t_{0}=t_{1}}} {0}=0} {0}=0}}} {0} {t_}}}}}}}}cc}cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccH0}cccH0}ccc \s_{n}=s_{n-1}+t_{n-1}=t_{0}+t_{1}+cdots ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################

Esto produce la presentación alternativa por orden, es decir, como tuplas n no decrecientes entre 0 y 1:

Δ Δ Alternativa Alternativa n={}()s1,...... ,sn)▪ ▪ Rn▪ ▪ 0=s0≤ ≤ s1≤ ≤ s2≤ ≤ ⋯ ⋯ ≤ ≤ sn≤ ≤ sn+1=1}.{displaystyle Delta En mathbb {R} {fn}mid} 0=s_{0}leq s_{1}leq s_{2}leq dots leq s_{n}leq S_{n+1}=1right}

Geométricamente, esto es un n- subconjunto dimensional Rn{displaystyle mathbb {R} {} {}} {fn}} (dimensión aproximada, codimensión 0) en lugar de Rn+1{displaystyle mathbb {R} {n+1} (codimensión 1). Las facetas, que en el simplex estándar corresponden a una coordenadas desapareciendo, ti=0,{displaystyle T_{i}=0,} aquí corresponde a coordenadas sucesivas siendo iguales, si=si+1,{displaystyle S_{i}=s_{i+1} mientras que el interior corresponde a las desigualdades que se están convirtiendo estricto (aumento de secuencias).

Una distinción clave entre estas presentaciones es el comportamiento bajo coordenadas permutadoras – el simplex estándar se estabiliza por coordenadas permutadoras, mientras que elementos permutadores del "ordenado simplex" no lo dejan invariante, ya que la permutación de una secuencia ordenada generalmente lo hace sin orden. De hecho, el simplex ordenado es un (cerrado) dominio fundamental para la acción del grupo simétrico sobre el n-cubo, lo que significa que la órbita del simplex ordenado bajo el n! elementos del grupo simétrico divide los n- ¡Cabrón! n!{displaystyle n!} principalmente simplices disjoint (disjoint excepto los límites), mostrando que este simplex tiene volumen 1/n!{displaystyle 1/n!} Alternativamente, el volumen puede ser calculado por una integral iterada, cuyos sucesivos componentes son 1,x,x2/2,x3/3!,...... ,xn/n!{displaystyle 1,x,x^{2}/2,x^{3}/3!,dotsx^{n}/n!

Otra propiedad de esta presentación es que usa el orden pero no la suma y, por lo tanto, puede definirse en cualquier dimensión sobre cualquier conjunto ordenado y, por ejemplo, puede usarse para definir un símplex de dimensión infinita sin problemas de convergencia de sumas

Proyección sobre el símplex estándar

Especialmente en aplicaciones numéricas de la teoría de la probabilidad una proyección sobre el simplex estándar es de interés. Dado ()pi)i{displaystyle (p_{i})_{i} con entradas posiblemente negativas, el punto más cercano ()ti)i{displaystyle left(t_{i}right)_{i} en el simplex tiene coordenadas

ti=max{}pi+Δ Δ ,0},{displaystyle t_{i}=max{p_{i}+ Delta ,0},}

Donde Δ Δ {displaystyle Delta } es elegido tal que .. imax{}pi+Δ Δ ,0}=1.{textstyle sum ¿Por qué? Delta ,0}=1.}

Δ Δ {displaystyle Delta } se puede calcular fácilmente desde la clasificación pi{displaystyle P_{i}. El enfoque de clasificación toma O()nlog⁡ ⁡ n){displaystyle O(nlog n)} complejidad, que puede mejorarse O()n){displaystyle O(n)} complejidad a través de algoritmos de determinación mediana. Proyectar sobre el simplex es computacionalmente similar a proyectar sobre el l l 1{displaystyle ell _{1} Bola.

Esquina del cubo

Finalmente, una variante simple es reemplazar "sumando 1" con "suma de como máximo 1"; esto aumenta la dimensión en 1, por lo que para simplificar la notación, la indexación cambia:

Δ Δ cn={}()t1,...... ,tn)▪ ▪ RnSilencio.. i=1nti≤ ≤ 1yti≥ ≥ 0para todosi}.{displaystyle Delta _{c}{n}=left{(t_{1},ldotst_{n})in mathbb {R} ^{n}~{ Bigg. ################################################################################################################################################################################################################################################################

Esto produce un n-simplex como una esquina del n-cubo, y es un simplex ortogonal estándar. Este es el simplex utilizado en el método simplex, que se basa en el origen y modela localmente un vértice en un politopo con n facetas.

Coordenadas cartesianas para un símplex regular n-dimensional en Rn

Una forma de escribir un periódico n-simplex en Rⁿ es elegir dos puntos para ser los dos primeros vértices, elegir un tercer punto para hacer un triángulo equilátero, elegir un cuarto punto para hacer un tetraedro regular, y así sucesivamente. Cada paso requiere ecuaciones satisfactorias que aseguren que cada vértice recién elegido, junto con los vértices previamente elegidos, forma un simplex regular. Hay varios conjuntos de ecuaciones que se pueden escribir y utilizar para este propósito. Estos incluyen la igualdad de todas las distancias entre vértices; la igualdad de todas las distancias de vértices al centro del simplex; el hecho de que el ángulo subtended a través del nuevo vértice por cualquier dos vértices previamente elegidos es π π /3{displaystyle pi /3}; y el hecho de que el ángulo subtended a través del centro del simplex por cualquier dos vértices es arccos⁡ ⁡ ()− − 1/n){displaystyle arccos(-1/n)}.

También es posible escribir directamente un n-simple regular particular en Rⁿ que puede luego traducirse, rotarse y escalarse como se desee. Una forma de hacer esto es la siguiente. Denote los vectores base de Rⁿ por e₁ hasta e _n. Comience con el (n − 1)-simplex estándar, que es la envolvente convexa de los vectores base. Al agregar un vértice adicional, estos se convierten en una cara de un n-simplex normal. El vértice adicional debe estar en la línea perpendicular al baricentro del símplex estándar, por lo que tiene la forma (α/n,..., α/n) para algún número real α. Dado que la distancia al cuadrado entre dos vectores base es 2, para que el vértice adicional forme un n-simple regular, la distancia al cuadrado entre él y cualquiera de los vectores base también debe ser 2. Esto produce una ecuación cuadrática para α. Resolver esta ecuación muestra que hay dos opciones para el vértice adicional:

1n()1± ± n+1)⋅ ⋅ ()1,...... ,1).{displaystyle {frac {1}{n}}left(1pm {sqrt {n+1}right)cdot (1,dots1). }

Cualquiera de estos, junto con los vectores base estándar, produce un n-simple regular.

El n-simple regular anterior no está centrado en el origen. Se puede trasladar al origen restando la media de sus vértices. Al cambiar la escala, se le puede dar la longitud del lado de la unidad. Esto da como resultado el símplex cuyos vértices son:

12ei− − 1n2()1± ± 1n+1)⋅ ⋅ ()1,...... ,1),{displaystyle {frac {1} {fnK}fnK} {f} {fnMicrosoft} ¿Qué? {1}{n{sqrt {2}} {bigg} {frac {1}{sqrt {n+1}}{bigg)}cdot (1,dots1),}}}

para 1≤ ≤ i≤ ≤ n{displaystyle 1leq ileq n}, y

± ± 12()n+1)⋅ ⋅ ()1,...... ,1).{displaystyle pm {frac {1}{sqrt {2(n+1)}}cdot (1,dots1). }

Tenga en cuenta que hay dos conjuntos de vértices descritos aquí. Un conjunto utiliza +{displaystyle +} en cada cálculo. El otro conjunto utiliza − − {displaystyle -} en cada cálculo.

Este sencillo se inscribe en una hipersfera de radio n/()2()n+1)){displaystyle {sqrt {n/(2(n+1)}}}.

Un cambio de escala diferente produce un símplex que se inscribe en una hiperesfera unitaria. Cuando se hace esto, sus vértices son

1+n− − 1⋅ ⋅ ei− − n− − 3/2()n+1± ± 1)⋅ ⋅ ()1,...... ,1),{displaystyle {sqrt {1+n^{-1}cdot} "Mathbf {e" ¿Por qué?

Donde 1≤ ≤ i≤ ≤ n{displaystyle 1leq ileq n}, y

± ± n− − 1/2⋅ ⋅ ()1,...... ,1).{displaystyle pm n^{-1/2}cdot (1,dots1). }

La longitud lateral de este simplex es 2()n+1)/n{fn}.

Una forma altamente simétrica de construir un n-simplex regular es usar una representación del grupo cíclico Z_n+1 por matrices ortogonales. Esta es una matriz ortogonal n × n Q tal que Qⁿ⁺¹ = I es la matriz de identidad, pero ninguna potencia inferior de Q lo es. La aplicación de potencias de esta matriz a un vector apropiado v producirá los vértices de un n-simple. Para llevar a cabo esto, primero observe que para cualquier matriz ortogonal Q, hay una elección de base en la que Q es una matriz diagonal de bloques

Q=diag⁡ ⁡ ()Q1,Q2,...... ,Qk),{displaystyle Q=operatorname {diag} (Q_{1},Q_{2},dotsQ_{k}),}

donde cada Q_i es ortogonal y 2 × 2 o 1 × 1. Para que Q tenga el orden n + 1, todos de estas matrices deben tener un orden que divida n + 1. Por lo tanto, cada Q_i es un 1 × 1 matriz cuya única entrada es 1 o, si n es impar, −1; o es una matriz 2 × 2 de la forma

()#⁡ ⁡ 2π π ⋅ ⋅ in+1− − pecado⁡ ⁡ 2π π ⋅ ⋅ in+1pecado⁡ ⁡ 2π π ⋅ ⋅ in+1#⁡ ⁡ 2π π ⋅ ⋅ in+1),{displaystyle {begin{pmatrix}cos {2fnMicroc} omega - ¿Qué? {fnMicroc} omega - ¿Qué? {fnMicroc {2ccH00} omega - ¿Qué? {fnMicroc} omega {} {n+1}end{pmatrix}}}

donde cada ω_i es un número entero entre cero y n inclusive. Una condición suficiente para que la órbita de un punto sea un símplex regular es que las matrices Q_i forman una base para las representaciones reales irreducibles no triviales de Z_n+1, y el vector que se está girando no está estabilizado por ninguno de ellos.

En términos prácticos, para n incluso esto significa que cada matriz Q _i es 2 × 2, hay una igualdad de conjuntos

{}⋅ ⋅ 1,n+1− − ⋅ ⋅ 1,...... ,⋅ ⋅ n/2,n+1− − ⋅ ⋅ n/2}={}1,...... ,n},{displaystyle {omega _{1},n+1-omega _{1},dotsomega _{n/2},n+1-omega ¿Qué?

y, para cada Q_i, las entradas de v sobre la cual Q_i los actos no son ambos cero. Por ejemplo, cuando n = 4, una matriz posible es

()#⁡ ⁡ ()2π π /5)− − pecado⁡ ⁡ ()2π π /5)00pecado⁡ ⁡ ()2π π /5)#⁡ ⁡ ()2π π /5)0000#⁡ ⁡ ()4π π /5)− − pecado⁡ ⁡ ()4π π /5)00pecado⁡ ⁡ ()4π π /5)#⁡ ⁡ ()4π π /5)).{displaystyle {begin{pmatrix}cos(2pi} /5) limitada-sin(2pi /5) limitada0\sin(2pi /5) /5) afectando 0 0 afectando 0 crecencos(4pi /5)sin(4pi /5) sufren0 sufrensin(4pi /5) afectandocos(4pi /5)end{pmatrix}.}

Aplicando esto al vector (1, 0, 1, 0) da como resultado el símplex cuyos vértices son

()1010),()#⁡ ⁡ ()2π π /5)pecado⁡ ⁡ ()2π π /5)#⁡ ⁡ ()4π π /5)pecado⁡ ⁡ ()4π π /5)),()#⁡ ⁡ ()4π π /5)pecado⁡ ⁡ ()4π π /5)#⁡ ⁡ ()8π π /5)pecado⁡ ⁡ ()8π π /5)),()#⁡ ⁡ ()6π π /5)pecado⁡ ⁡ ()6π π /5)#⁡ ⁡ ()2π π /5)pecado⁡ ⁡ ()2π π /5)),()#⁡ ⁡ ()8π π /5)pecado⁡ ⁡ ()8π π /5)#⁡ ⁡ ()6π π /5)pecado⁡ ⁡ ()6π π /5)),{end{pmatrix}}} {begin{pmatrix}cos(2pi} /5)\sin(2pi /5)\cos(4pi /5)\\sin(4pi /5)end{pmatrix}}},{begin{pmatrix}cos(4pi} /5)\sin(4pi /5)\cos(8pi /5)\\sin(8pi /5)end{pmatrix}}},{begin{pmatrix}cos(6pi} /5)\sin(6pi /5)\cos(2pi /5)\sin(2pi /5)end{pmatrix}},{begin{pmatrix}cos(8pi /5)\sin(8pi /5)\cos(6pi /5)\cos(6pi5pe0}end{pMatrix}

cada uno de los cuales tiene una distancia √5 de los demás. Cuando n es impar, la condición significa que exactamente uno de los bloques diagonales es 1 × 1, igual a −1, y actúa sobre una entrada distinta de cero de v; mientras que los bloques diagonales restantes dicen Q₁,..., Q_{(n − 1) / 2}, son 2 × 2, existe una igualdad de conjuntos

{}⋅ ⋅ 1,− − ⋅ ⋅ 1,...... ,⋅ ⋅ ()n− − 1)/2,− − ⋅ ⋅ n− − 1)/2}={}1,...... ,()n− − 1)/2,()n+3)/2,...... ,n},{displaystyle left{omega ################################################################################################################################################################################################################################################################ _{1},dotsomega _{(n-1)/2},-omega ¿Por qué?

y cada bloque diagonal actúa sobre un par de entradas de v que no son cero. Entonces, por ejemplo, cuando n = 3, la matriz puede ser

()0− − 1010000− − 1).{displaystyle {begin{pmatrix}0 ventaja-1 limitada01 doble0}}}

Para el vector (1, 0, 1/√ 2), el símplex resultante tiene vértices

()101/√ √ 2),()01− − 1/√ √ 2),()− − 101/√ √ 2),()0− − 1− − 1/√ √ 2),{fnMicrosoft Sans Serif}, {fnMicrosoft Sans Serif}, {begin{pmatrix}011111end{pmatrix}},{begin{pmatrix}-1p1p1}pmp1p1pMatrixcH0}

cada uno de los cuales tiene una distancia de 2 de los demás.

Propiedades geométricas

Volumen

El volumen de un n-simplex en un espacio n-dimensional con vértices (v₀,..., v_n) es

Volume=1n!SilencioDet()v1− − v0v2− − v0⋯ ⋯ vn− − v0)Silencio{displaystyle mathrm {Volume} ={frac {1}}}}left upondet {begin{pmatrix}v_{1}-v_{0} limitv_{2}-v_{0} {0} {0} {0} {0} {0}}}}}}}}derech}

donde cada columna de la n×n determinante es un vector que apunta desde el vértice v₀ a otro vértice v_k. Esta fórmula es particularmente útil cuando v0{displaystyle V_{0} es el origen.

La expresión

Volume=1n!Det[()v1T− − v0Tv2T− − v0T⋮ ⋮ vnT− − v0T)()v1− − v0v2− − v0⋯ ⋯ vn− − v0)]1/2{displaystyle mathrm {Volume} ={frac {1}}det left[{begin{pmatrix}v_{1} {T}-v_{0}\v_{2} {0} {0} {0} {0}\cH0}\cdots\cdots}\cdots}cdots} {0} {0}}}\cH00}cH00}cH0}cH00}cH00}cH00}cH00}cH00}}cH00}ccH00}ccH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}ccH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}ccH00} \v_{n} {T}-v_{0} {T}end{pmatrix}{begin{pmatrix}v_{1}-v_{0} limitv_{2}-v_{0} {fn} {fn} {fnMicrosoft}} {fnMicrosoft}}

emplea un determinante Gram y funciona incluso cuando el n- Los vértices del complejo están en un espacio euclidiano con más que n dimensiones, por ejemplo, un triángulo en R3{displaystyle mathbb {R} {} {}}}.

Una manera más simétrica de calcular el volumen de un n-simplex en Rn{displaystyle mathbb {R} {} {}} {fn}} es

Volume=1n!SilencioDet()v0v1⋯ ⋯ vn11⋯ ⋯ 1)Silencio.{displaystyle mathrm {Volume} ={1 over n!}left toleradet {begin{pmatrix}v_{0} limitv_{1} Ahora mismo.

Otra forma común de calcular el volumen del simplex es a través del determinante de Cayley-Menger, que funciona incluso cuando los vértices del n-simplex están en un espacio euclidiano con más de n dimensiones.

Sin el 1/n! es la fórmula para el volumen de un n- Parallelotope. Esto puede entenderse como sigue: Supongamos que P es un n-parallelotope construido sobre una base ()v0,e1,...... ,en){displaystyle (v_{0},e_{1},ldotse_{n}} de Rn{displaystyle mathbb {R} {} {}} {fn}}. Dada una permutación σ σ {displaystyle sigma } de {}1,2,...... ,n}{displaystyle {1,2,ldotsn}, llame a una lista de vértices v0,v1,...... ,vn{displaystyle v_{0}, v_{1},ldotsv_{n} a n- Si.

v1=v0+eσ σ ()1),v2=v1+eσ σ ()2),...... ,vn=vn− − 1+eσ σ ()n){displaystyle v_{1}=v_{0}+e_{sigma (1)}, v_{2}=v_{1}+e_{sigma (2)},ldotsv_{n}=v_{n-1}+e_{sigma (n)}

(así que hay n!n-patas y vn{displaystyle V_{n} no depende de la permutación). Las siguientes afirmaciones sostienen:

Si P es la unidad n-hipercubo, entonces la unión de los n-simples formados por el casco convexo de cada n-path es P, y estos símplex son congruentes y no se superponen por pares. En particular, el volumen de tal símplex es

Vol⁡ ⁡ ()P)n!=1n!.{displaystyle {frac {fnMicroc} {Vol} {fn}}={frac} {1} {n}}}.}

Si P es un paraleótopo general, las mismas afirmaciones sostienen excepto que ya no es verdad, en la dimensión 2, que los simplexes necesitan ser congruentes pares; sin embargo sus volúmenes permanecen iguales, porque los n-parallelotope es la imagen de la unidad n-hipercubo por el isomorfismo lineal que envía la base canónica de Rn{displaystyle mathbb {R} {} {}} {fn}} a e1,...... ,en{displaystyle e_{1},ldotse_{n}. Como antes, esto implica que el volumen de un simplex procedente de un n- El camino es:

Vol⁡ ⁡ ()P)n!=Det()e1,...... ,en)n!.{displaystyle {frac {fnMicroc} {Vol} {fn}}={frac {det(e_{1},ldotse_{n}} {n}}}}}}} {n}} {fn}} {fn}}} {fn}}}} {fn}} {fn}}}} {fn}} {fn}}}}}}} {f}}}}} {fn}}}} {fn}}}}}} {f}}}}} {f}}}}}} {f}}} {fn}}}}}}}}}}}}}}}}}}}}}}} {f}}} {f}}} {fn}}} {f}} {f} {f}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

Por el contrario, dada una n-simplex ()v0,v1,v2,...... vn){displaystyle (v_{0}, v_{1}, v_{2},ldots v_{n}} de Rn{displaystyle mathbf {R} {n}, se puede suponer que los vectores e1=v1− − v0,e2=v2− − v1,...... en=vn− − vn− − 1{displaystyle e_{1}=v_{1}-v_{0}, e_{2}=v_{1},ldots E_{n}=v_{n}-v_{n-1} forma una base de Rn{displaystyle mathbf {R} {n}. Considerando el paraleópo construido a partir de v0{displaystyle V_{0} y e1,...... ,en{displaystyle e_{1},ldotse_{n}, se ve que la fórmula anterior es válida para cada simplex.

Finalmente, la fórmula al principio de esta sección se obtiene observando que

Det()v1− − v0,v2− − v0,...... ,vn− − v0)=Det()v1− − v0,v2− − v1,...... ,vn− − vn− − 1).{displaystyle det(v_{1}-v_{0},v_{2}-v_{0},ldotsv_{n}-v_{0})=det(v_{1}-v_{0},v_{2}-v_{1},ldotsv_{n}-v_{n-1}). }

De esta fórmula, se deduce inmediatamente que el volumen bajo un estándar n-simplex (es decir, entre el origen y el simplex en R^{n +1}) es

1()n+1)!{displaystyle {1 over (n+1)!}

El volumen de un n-símplex regular con longitud de lado unidad es

n+1n!2n{displaystyle {frac {sqrt {n+1}{n!{sqrt {2}}}}

como se puede ver multiplicando la fórmula anterior por x^{n+ 1}, para conseguir el volumen bajo el n-simplex como una función de su distancia del vértice x del origen, diferenciando con respecto a x, a x=1/2{displaystyle x=1/{sqrt {2}}(donde n- Longitud lateral del complejo es 1), y normalización por la longitud dx/n+1{displaystyle dx/{sqrt {n+1}} del aumento, ()dx/()n+1),...... ,dx/()n+1)){displaystyle (dx/(n+1),ldotsdx/(n+1)}, a lo largo del vector normal.

Ángulos diedros del n-simple regular

Cualesquiera caras de dos (n − 1) dimensiones de un símplex regular de n dimensiones son regulares (n − 1)- simples dimensionales, y tienen el mismo ángulo diedro de cos⁻¹(1/n).

Esto se puede ver notando que el centro del simplex estándar es ()1n+1,...... ,1n+1){textstyle left {frac {1}{n+1}},dots{frac {1}{n+1}}right)}, y los centros de sus rostros se coordinan permutaciones ()0,1n,...... ,1n){textstyle left(0,{frac {1}{n}dots{frac {1}{n}right)}. Entonces, por simetría, el vector apuntando desde ()1n+1,...... ,1n+1){textstyle left {frac {1}{n+1}},dots{frac {1}{n+1}}right)} a ()0,1n,...... ,1n){textstyle left(0,{frac {1}{n}dots{frac {1}{n}right)} es perpendicular a las caras. Así que los vectores normales a las caras son permutaciones de ()− − n,1,...... ,1){displaystyle (-n,1,dots1)}, desde el cual se calculan los ángulos dihedral.

Simplifica con una "esquina ortogonal"

Una "esquina ortogonal" significa aquí que hay un vértice en el que todos los bordes adyacentes son ortogonales por pares. Inmediatamente se sigue que todas las caras adyacentes son ortogonales por pares. Tales simples son generalizaciones de triángulos rectángulos y para ellos existe una versión n-dimensional del teorema de Pitágoras:

La suma de los volúmenes dimensionales al cuadrado (n − 1) de las facetas adyacentes a la esquina ortogonal es igual al volumen dimensional al cuadrado (n − 1) de la cara opuesta a la esquina ortogonal.

.. k=1nSilencioAkSilencio2=SilencioA0Silencio2{displaystyle sum _{k=1}{n}SobrevivirA_{k} _{2}

Donde A1...... An{displaystyle A_{1}ldots A_{n} son facetas que son ortogonales pares entre sí pero no ortogonales para A0{displaystyle A_{0}, que es la faceta frente a la esquina ortogonal.

Para un 2-simple el teorema es el teorema de Pitágoras para triángulos con un ángulo recto y para un 3-simple es el teorema de Gua para un tetraedro con una esquina ortogonal.

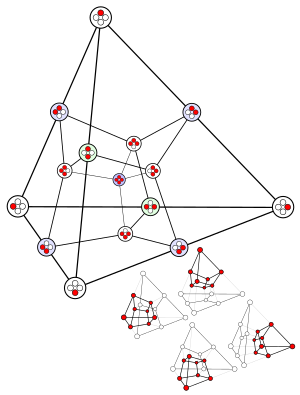
Relación con el hipercubo (n + 1)

El diagrama de Hasse de la red de caras de un n-simple es isomorfo al gráfico de las aristas del (n + 1)-hipercubo, con los vértices del hipercubo se asignan a cada uno de los elementos n-simplex, incluido el símplex completo y el politopo nulo como los puntos extremos de la red (asignados a dos vértices opuestos en el hipercubo). Este hecho se puede utilizar para enumerar eficientemente la red de caras del símplex, ya que los algoritmos de enumeración de redes de caras más generales son más costosos desde el punto de vista computacional.

El n-simplex es también la figura del vértice del (n + 1)-hipercubo. También es la faceta del (n + 1)-orthoplex.

Topología

Topológicamente, un n-simplex es equivalente a una n-bola. Cada n-simplex es una variedad n-dimensional con esquinas.

Probabilidad

En la teoría de la probabilidad, los puntos del estándar n-simple en (n + 1)-espacio forman el espacio de posibles distribuciones de probabilidad en un conjunto finito que consta de n + 1 resultados posibles. La correspondencia es la siguiente: Para cada distribución descrita como una tupla ordenada (n+ 1) de probabilidades cuya suma es (necesariamente) 1, asociamos el punto del símplex cuyas coordenadas baricéntricas son precisamente aquellas probabilidades Es decir, se asigna al késimo vértice del símplex para que tenga la késima probabilidad de la tupla (n + 1) como su coeficiente baricéntrico. Esta correspondencia es un homeomorfismo afín.

Compuestos

Dado que todos los simples son autoduales, pueden formar una serie de compuestos;

• Dos triángulos forman un hexagrama {6/2}.
• Dos tetrahedra forman un compuesto de dos tetrahedra o estelar octangula.
• Dos 5 celdas forman un compuesto de dos 5 celdas en cuatro dimensiones.

Topología algebraica

En la topología algebraica, los simples se utilizan como bloques de construcción para construir una clase interesante de espacios topológicos llamados complejos simpliciales. Estos espacios se construyen a partir de simples pegados entre sí de forma combinatoria. Los complejos simpliciales se utilizan para definir un cierto tipo de homología llamada homología simplicial.

Un conjunto finito de k-simplex incrustados en un subconjunto abierto de Rⁿ se denomina cadena afín k. Los simples en una cadena no necesitan ser únicos; pueden ocurrir con multiplicidad. En lugar de utilizar la notación de conjunto estándar para denotar una cadena afín, la práctica estándar es utilizar signos más para separar cada miembro del conjunto. Si algunos de los símplex tienen la orientación opuesta, se anteponen con un signo menos. Si algunos de los símplexes aparecen en el conjunto más de una vez, se anteponen con un número entero. Así, una cadena afín toma la forma simbólica de una suma con coeficientes enteros.

Tenga en cuenta que cada faceta de un n-simple es un afín (n − 1)-simple y, por lo tanto, el límite de un n-simplex es una cadena afín (n − 1). Por lo tanto, si denotamos un símplex afín positivamente orientado como

σ σ =[v0,v1,v2,...... ,vn]{displaystyle sigma =[v_{0},v_{1},v_{2},ldotsv_{n}}

con el vj{displaystyle v_{j} denotando los vértices, luego el límite ∂ ∂ σ σ {displaystyle partial sigma } de σ es la cadena

∂ ∂ σ σ =.. j=0n()− − 1)j[v0,...... ,vj− − 1,vj+1,...... ,vn].{displaystyle partial sigma =sum _{j=0}{n}(-1)^{j}[v_{0},ldotsv_{j-1},v_{j+1},ldotsv_{n}].}

Se deduce de esta expresión, y de la linealidad del operador de límite, que el límite del límite de un símplex es cero:

∂ ∂ 2σ σ =∂ ∂ ().. j=0n()− − 1)j[v0,...... ,vj− − 1,vj+1,...... ,vn])=0.{displaystyle partial ^{2}sigma =partial left(sum _{j=0}{n}(-1)^{j}[v_{0},ldotsv_{j-1},v_{j+1},ldotsv_{n}]right)=0}

Asimismo, el límite del límite de una cadena es cero: ∂ ∂ 2*** *** =0{displaystyle partial ^{2}rho =0}.

Más generalmente, un simplex (y una cadena) se puede incrustar en un múltiple por medio de mapa suave y diferenciable f:: Rn→ → M{displaystyle fcolon mathbb {R}{n}to M.. En este caso, tanto la convención de summation para denotar el conjunto, como la operación de límite concuerda con la incrustación. Eso es,

f().. iaiσ σ i)=.. iaif()σ σ i){displaystyle fleft(sum nolimits ¿Qué? _{i}right)=sum nolimits _{i}a_{i}f(sigma _{i})}

Donde ai{displaystyle A_{i} son los enteros denotando orientación y multiplicidad. Para el operador de límites ∂ ∂ {displaystyle partial }, uno tiene:

∂ ∂ f()*** *** )=f()∂ ∂ *** *** ){displaystyle partial f(rho)=f(partial rho)}

donde ρ es una cadena. La operación de contorno conmuta con el mapeo porque, al final, la cadena se define como un conjunto y poco más, y la operación de conjunto siempre conmuta con la operación de mapeo (por definición de un mapeo).

Un mapa continuo f:σ σ → → X{displaystyle f:sigma to X} a un espacio topológico X se conoce con frecuencia como singular n-simplex. (Un mapa generalmente se llama "singular" si no tiene alguna propiedad deseable como la continuidad y, en este caso, el término está destinado a reflejar el hecho de que el mapa continuo no necesita ser una incrustación.)

Geometría algebraica

Dado que la geometría algebraica clásica permite hablar de ecuaciones polinómicas pero no de desigualdades, el estándar algebraico n-simplex se define comúnmente como el subconjunto de afines (n + 1)-espacio dimensional, donde todas las coordenadas suman 1 (dejando así fuera la parte de la desigualdad). La descripción algebraica de este conjunto es

Δ Δ n:={}x▪ ▪ An+1Silencio.. i=1n+1xi=1},{displaystyle Delta ^{n}:=left{xin mathbb {A} ^{n+1}~{ Bigg. ¿Qué?

que equivale a la descripción teórica del esquema Δ Δ n()R)=Específico⁡ ⁡ ()R[Δ Δ n]){displaystyle Delta _{n}(R)=operatorname (R[Delta ^{n})} con

R[Δ Δ n]:=R[x1,...... ,xn+1]/()1− − .. xi){displaystyle R[Delta ^{n}]:=R[x_{1},ldotsx_{n+1}left/left(1-sum x_{i}right)right.}

el anillo de funciones regulares en el algebraico n-simplex (para cualquier anillo) R{displaystyle R.).

Usando las mismas definiciones que para el clásico n-simplex, el n-simplices para diferentes dimensiones n ensamblar en un objeto simplicial, mientras los anillos R[Δ Δ n]{displaystyle R[Delta ^{n} ensamblar en un objeto cosimplicial R[Δ Δ ∙ ∙ ]{displaystyle R[Delta ^{bullet] (en la categoría de esquemas resp. anillos, ya que los mapas faciales y degenerativos son todos polinomios).

Los n-simples algebraicos se utilizan en la teoría K superior y en la definición de grupos Chow superiores.

Aplicaciones

• En las estadísticas, los simplices son espacios de muestra de datos compositivos y también se utilizan en cantidades de trama que suman a 1, como proporciones de subpoblaciones, como en una parcela ternaria.
• En las estadísticas industriales surgen simplices en la formulación de problemas y en solución algorítmica. En el diseño del pan, el productor debe combinar levadura, harina, agua, azúcar, etc. En tales mezclas, sólo importan las proporciones relativas de los ingredientes: Para una mezcla óptima de pan, si la harina se dobla, la levadura debe doblarse. Este problema de mezcla se formula a menudo con limitaciones normalizadas, de modo que los componentes no negativos se suman a uno, en cuyo caso la región viable forma un simplex. La calidad de las mezclas de pan se puede estimar utilizando metodología de superficie de respuesta, y luego se puede calcular un máximo local utilizando un método de programación no lineal, como la programación cuadrática secuencial.
• En la investigación de operaciones, los problemas de programación lineal pueden ser resueltos por el algoritmo simplex de George Dantzig.
• En el diseño geométrico y gráficos de computadora, muchos métodos primero realizan triangulaciones simpliciales del dominio y luego encajan polinomios interpoladores a cada simplex.
• En la química, los hidratos de la mayoría de los elementos del p-block pueden parecerse a un simplex si se quiere conectar cada átomo. Neon no reacciona con hidrógeno y como tal es un punto, los enlaces fluorinos con un átomo de hidrógeno y forma un segmento de línea, los enlaces de oxígeno con dos átomos de hidrógeno en una forma doblada que se asemejan a un triángulo, nitrógeno reacciona para formar un tetraedro, y el carbono forma una estructura que se parece a un diagrama de Schlegel de las 5 células. Esta tendencia continúa por los análogos más pesados de cada elemento, así como si el átomo de hidrógeno es reemplazado por un átomo de halógeno.
• En algunos enfoques de la gravedad cuántica, como Regge cálculo y triangulaciones dinámicas causales, los simplices se utilizan como bloques de construcción de discretizaciones de tiempo espacial; es decir, para construir manifolds simpliciales.