Simón Stevin

Simon Stevin (holandés: [ˈsimɔn ˈsteːvɪn]; 1548–1620), a veces llamado Stevinus, fue un matemático, científico y teórico de la música flamenco. Hizo diversas contribuciones en muchas áreas de la ciencia y la ingeniería, tanto teóricas como prácticas. También tradujo varios términos matemáticos al holandés, convirtiéndolo en uno de los pocos idiomas europeos en los que la palabra matemáticas, wiskunde (wis y kunde, es decir, "el conocimiento de lo que es cierto"), no era un préstamo del griego sino un calco vía latín. También reemplazó la palabra chemie, el holandés para química, por scheikunde ("el arte de separar"), hecho en analogía con wiskunde .

Biografía

Se sabe muy poco con certeza sobre la vida de Simon Stevin, y lo que sabemos se infiere principalmente de otros hechos registrados. La fecha exacta de nacimiento y la fecha y lugar de su muerte son inciertas. Se supone que nació en Brujas, ya que se matriculó en la Universidad de Leiden con el nombre de Simon Stevinus Brugensis (que significa "Simon Stevin de Brujas"). Su nombre generalmente se escribe como Stevin, pero algunos documentos sobre su padre usan la ortografía Stevijn (pronunciación [ˈste:vεɪn]); este fue un cambio ortográfico común en el holandés del siglo XVI. La madre de Simon Stevin, Cathelijne (o Catelyne), era hija de una familia rica de Ypres; su padre Hubert era un pobre de Brujas. Cathelijne se casaría más tarde con Joost Sayon, quien estaba involucrado en el comercio de alfombras y seda y era miembro de schuttersgilde Sint-Sebastiaan. A través de su matrimonio, Cathelijne se convirtió en miembro de una familia de calvinistas; se cree que Simon Stevin probablemente se crió en la fe calvinista.

Se cree que Stevin creció en un ambiente relativamente próspero y disfrutó de una buena educación. Probablemente fue educado en una escuela de latín en su ciudad natal.

Los viajes de Simon Stevin

Stevin salió de Brujas en 1571 aparentemente sin un destino particular. Lo más probable es que Stevin fuera calvinista, ya que un católico probablemente no habría ascendido al puesto de confianza que más tarde ocupó con Mauricio, Príncipe de Orange. Se supone que salió de Brujas para escapar de la persecución religiosa de los protestantes por parte de los gobernantes españoles. Sobre la base de referencias en su obra "Wisconstighe Ghedaechtenissen" (Memorias matemáticas), se ha inferido que debe haberse mudado primero a Amberes, donde comenzó su carrera como comerciante' empleado de s. Algunos biógrafos mencionan que viajó a Prusia, Polonia, Dinamarca, Noruega y Suecia y otras partes del norte de Europa, entre 1571 y 1577. Es posible que realizara estos viajes en un período de tiempo más largo. En 1577, Simon Stevin regresó a Brujas y los concejales de Brujas lo nombraron secretario municipal, cargo que ocupó entre 1577 y 1581. Trabajó en la oficina de Jan de Brune de Brugse Vrije, la castellanía de Brujas.

No está claro por qué había regresado a Brujas en 1577. Puede haber estado relacionado con los acontecimientos políticos de ese período. Brujas fue escenario de intensos conflictos religiosos. Católicos y calvinistas controlaban alternativamente el gobierno de la ciudad. Por lo general, se oponían entre sí, pero ocasionalmente colaboraban para contrarrestar los dictados del rey Felipe II de España. En 1576 se decretó un cierto nivel de tolerancia religiosa oficial. Esto podría explicar por qué Stevin regresó a Brujas en 1577. Más tarde, los calvinistas tomaron el poder en muchas ciudades flamencas y encarcelaron a clérigos católicos y gobernadores seculares que apoyaban a los gobernantes españoles. Entre 1578 y 1584 Brujas estuvo gobernada por los calvinistas.

Simon Stevin en Holanda

En 1581, Stevin volvió a dejar su Brujas natal y se mudó a Leiden, donde asistió a la escuela de latín. El 16 de febrero de 1583 se matriculó, bajo el nombre de Simon Stevinus Brugensis (que significa "Simon Stevin de Brujas"), en la Universidad de Leiden, que había sido fundada por Guillermo el Silencioso en 1575. Aquí se hizo amigo del segundo hijo y heredero de Guillermo el Silencioso, el príncipe Mauricio, el conde de Nassau. Stevin figura en los registros de la Universidad hasta 1590 y aparentemente nunca se graduó.

Tras el asesinato de Guillermo el Silencioso y la toma de posesión del cargo de su padre por parte del príncipe Mauricio, Stevin se convirtió en el principal asesor y tutor del príncipe Mauricio. El príncipe Mauricio le pidió consejo en muchas ocasiones y lo nombró funcionario público: en primer director del llamado "waterstaet" (la autoridad gubernamental para las obras públicas, especialmente la gestión del agua) desde 1592, y más tarde intendente general del ejército de los Estados Generales. El príncipe Mauricio también le pidió a Stevin que fundara una escuela de ingeniería dentro de la Universidad de Leiden.

Stevin se mudó a La Haya donde compró una casa en 1612. Se casó en 1610 o 1614 y tuvo cuatro hijos. Se sabe que dejó viuda con dos hijos a su muerte en Leiden o La Haya en 1620.

• 

  Estatua de Simon Stevin por Eugène Simonis, en el Simon Stevinplein[nl] en Brujas

• 

  Estatua de Stevin (detalle)

• 

  Estatua (detalle): Diagrama de plano inclinado

• 

  Estatua (detalle) mostrando experimentos en equilibrio hidrostático

Descubrimientos e inventos

Carro de viento o yate terrestre (Zeilwagen) diseñado por Simon Stevin para el Príncipe Maurice de Orange (grabado por Jacques de Gheyn).

Stevin es responsable de muchos descubrimientos e inventos. Fue un pionero del desarrollo y la aplicación práctica de las ciencias (relacionadas con la ingeniería) como las matemáticas, la física y las ciencias aplicadas como la ingeniería hidráulica y la agrimensura. Se pensó que había inventado las fracciones decimales hasta mediados del siglo XX, cuando los investigadores descubrieron que las fracciones decimales habían sido previamente introducidas por el erudito islámico medieval al-Uqlidisi en un libro escrito en 952. Además, un desarrollo sistemático de fracciones decimales fue dada mucho antes que Stevin en el libro Miftah al-Hisab escrito en 1427 por Al-Kashi.

Sus contemporáneos quedaron muy impresionados por su invención del llamado yate terrestre, un carruaje con velas, del cual se conservó un modelo en Scheveningen hasta 1802. El carruaje en sí se había perdido mucho antes. Alrededor del año 1600, Stevin, con el príncipe Mauricio de Orange y otros veintiséis, utilizaron el carruaje en la playa entre Scheveningen y Petten. El carruaje era impulsado únicamente por la fuerza del viento y adquiría una velocidad que excedía a la de los caballos.

Gestión de cursos de agua

El trabajo de Stevin en el waterstaet implicó mejoras en las esclusas y aliviaderos para controlar inundaciones, ejercicios de ingeniería hidráulica. Los molinos de viento ya estaban en uso para bombear el agua, pero en Van de Molens (On mills), sugirió mejoras, incluidas ideas de que las ruedas deberían moverse lentamente con un mejor sistema para engrane de los dientes del engranaje. Estos triplicaron la eficiencia de los molinos de viento utilizados para bombear agua fuera de los pólderes. Recibió una patente sobre su innovación en 1586.

Filosofía de la ciencia

El objetivo de Stevin era generar una segunda era de sabiduría, en la que la humanidad habría recuperado todo su conocimiento anterior. Dedujo que la lengua hablada en esta época tendría que ser el holandés, porque, como demostró empíricamente, en esa lengua se podían indicar más conceptos con palabras monosilábicas que en cualquiera de las lenguas (europeas) con las que la había comparado. Esta fue una de las razones por las que escribió todas sus obras en holandés y dejó su traducción para que la hicieran otros. La otra razón era que quería que sus obras fueran útiles en la práctica para personas que no dominaban el lenguaje científico común de la época, el latín. Gracias a Simon Stevin, el idioma holandés obtuvo su vocabulario científico adecuado, como "wiskunde" ("kunst van het gewisse of zekere" el arte de lo que se sabe o lo que es cierto) para las matemáticas, "natuurkunde" (el "arte de la naturaleza") para la física, "scheikunde" (el "arte de la separación") para química, "sterrenkunde" (el "arte de las estrellas") para astronomía, "meetkunde" (el "arte de medir") para la geometría.

Geometría, física y trigonometría

La prueba de Stevin de la ley del equilibrio en un plano inclinado, conocido como el "Epitaph de Stevinus".

Stevin fue el primero en mostrar cómo modelar poliedros regulares y semirregulares delineando sus marcos en un plano. También distinguió los equilibrios estables de los inestables.

Stevin contribuyó a la trigonometría con su libro, De Driehouckhandel.

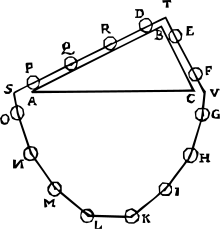
En EL PRIMER LIBRO DE LOS ELEMENTOS DEL ARTE DE PESAR, Segunda parte: De las proposiciones [Las Propiedades de los Pesos Oblicuos], Página 41, Teorema XI, Proposición XIX, derivó la condición para el equilibrio de fuerzas en planos inclinados utilizando un diagrama con una "corona de flores" que contiene masas redondas espaciadas uniformemente que descansan sobre los planos de un prisma triangular (ver la ilustración al lado). Llegó a la conclusión de que los pesos requeridos eran proporcionales a la longitud de los lados sobre los que descansaban, suponiendo que el tercer lado fuera horizontal y que el efecto de un peso se reducía de manera similar. Está implícito que el factor de reducción es la altura del triángulo dividida por el lado (el seno del ángulo del lado con respecto a la horizontal). El diagrama de prueba de este concepto se conoce como el "Epitafio de Stevinus". Como señaló E. J. Dijksterhuis, la prueba del equilibrio de Stevin en un plano inclinado puede criticarse por usar el movimiento perpetuo para implicar una reducción al absurdo. Dijksterhuis dice que Stevin "intuitivamente hizo uso del principio de conservación de la energía... mucho antes de que fuera formulado explícitamente".

Demostró la resolución de fuerzas ante Pierre Varignon, lo que no había sido comentado anteriormente, aunque es una simple consecuencia de la ley de su composición.

Stevin descubrió la paradoja hidrostática, que establece que la presión en un líquido es independiente de la forma del recipiente y el área de la base, pero depende únicamente de su altura.

También dio la medida de la presión en cualquier parte del costado de un recipiente.

Fue el primero en explicar las mareas usando la atracción de la luna.

En 1586 demostró que dos objetos de diferente peso caen con la misma aceleración.

Teoría musical

Van de Spiegheling der singconst.

La primera mención del temperamento igual relacionado con la raíz doceava de dos en Occidente apareció en el manuscrito inacabado de Simon Stevin Van de Spiegheling der singconst(ca 1605) publicado póstumamente hace trescientos años. más tarde en 1884; sin embargo, debido a la precisión insuficiente de su cálculo, muchos de los números (para la longitud de la cadena) que obtuvo estaban separados por una o dos unidades de los valores correctos. Parece haberse inspirado en los escritos del laudista y teórico musical italiano Vincenzo Galilei (padre de Galileo Galilei), antiguo alumno de Gioseffo Zarlino.

Contabilidad

Es posible que Stevin conociera la contabilidad por partida doble, ya que era un empleado en Amberes en su juventud, ya sea prácticamente o a través de las obras de autores italianos como Luca Pacioli y Gerolamo Cardano. Sin embargo, Stevin fue el primero en recomendar el uso de cuentas impersonales en el hogar nacional. Lo puso en práctica para el príncipe Mauricio y lo recomendó al estadista francés Sully.

Fracciones decimales

Stevin escribió un folleto de 35 páginas llamado De Thiende ("el arte de las décimas"), publicado por primera vez en holandés en 1585 y traducido al francés como La Disme . El título completo de la traducción al inglés era Aritmética decimal: enseñanza de cómo realizar todos los cálculos con números enteros sin fracciones, mediante los cuatro principios de la aritmética común: suma, resta, multiplicación y división. Los conceptos a los que se hace referencia en el folleto incluyen fracciones unitarias y fracciones egipcias. Los matemáticos musulmanes fueron los primeros en utilizar decimales en lugar de fracciones a gran escala. El libro de Al-Kashi, Clave de la aritmética, fue escrito a principios del siglo XV y fue el estímulo para la aplicación sistemática de decimales a números enteros y fracciones de los mismos. Pero nadie estableció su uso diario antes que Stevin. Sintió que esta innovación era tan significativa que declaró que la introducción universal de monedas, medidas y pesos decimales era simplemente una cuestión de tiempo.

Su notación es bastante difícil de manejar. El punto que separa los números enteros de las fracciones decimales parece ser invención de Bartholomaeus Pitiscus, en cuyas tablas trigonométricas (1612) aparece, y fue aceptado por John Napier en sus artículos logarítmicos (1614 y 1619).

Stevin imprimió pequeños círculos alrededor de los exponentes de las diferentes potencias de una décima. Que Stevin pretendía que estos números encerrados en un círculo denotaran meros exponentes queda claro por el hecho de que empleó el mismo símbolo para potencias de cantidades algebraicas. No evitó los exponentes fraccionarios; sólo los exponentes negativos no aparecen en su obra.

Stevin escribió sobre otros temas científicos, por ejemplo, óptica, geografía, astronomía, y varios de sus escritos fueron traducidos al latín por W. Snellius (Willebrord Snell). Hay dos ediciones completas en francés de sus obras, ambas impresas en Leiden, una en 1608 y la otra en 1634.

Matemáticas

Oeuvres mathematiques, 1634

Stevin escribió su Aritmética en 1594. El trabajo trajo al mundo occidental por primera vez una solución general de la ecuación cuadrática, documentada originalmente casi un milenio antes por Brahmagupta en la India.

Según Van der Waerden, Stevin eliminó "la restricción clásica de 'números' a números enteros (Euclides) oa fracciones racionales (Diophantos)... los números reales formaban un continuo. Su noción general de un número real fue aceptada, tácita o explícitamente, por todos los científicos posteriores. Un estudio reciente atribuye un mayor papel a Stevin en el desarrollo de los números reales de lo que han reconocido los seguidores de Weierstrass. Stevin demostró el teorema del valor intermedio para polinomios, anticipándose a la demostración de Cauchy. Stevin utiliza un procedimiento de divide y vencerás, subdividiendo el intervalo en diez partes iguales. Los decimales de Stevin fueron la inspiración para el trabajo de Isaac Newton sobre las series infinitas.

Neologismos

Stevin pensó que el idioma holandés era excelente para la redacción científica y tradujo muchos de los términos matemáticos al holandés. Como resultado, el holandés es uno de los pocos idiomas de Europa occidental que tiene muchos términos matemáticos que no se derivan del griego ni del latín. Esto incluye el mismo nombre wiskunde (matemáticas).

Su ojo para la importancia de que el lenguaje científico sea el mismo que el lenguaje del artesano puede mostrarse en la dedicatoria de su libro De Thiende ('The Disme' o 'The Tenth'): 'Simon Stevin les desea buena suerte a los observadores de estrellas, topógrafos, medidores de alfombras, medidores corporales en general, medidores de monedas y comerciantes.' Más adelante en el mismo folleto, escribe: "[este texto] nos enseña todos los cálculos que necesita la gente sin usar fracciones. Se pueden reducir todas las operaciones a sumar, restar, multiplicar y dividir con números enteros."

Algunas de las palabras que inventó evolucionaron: 'aftrekken' (restar) y 'eliminar' (dividir) permaneció igual, pero con el tiempo 'menigvuldigen' se convirtió en 'vermenigvuldigen' (multiplicar, el agregado 'ver' enfatiza el hecho de que es una acción). 'Vergaderen' (reunión) se convirtió en 'optellen' (añadir lit. contar).

Otro ejemplo es la palabra holandesa para diámetro: 'middellijn', lit.: línea a través del medio.

La palabra 'zomenigmaal' (cociente lit. 'que muchas veces') se ha convertido en el tal vez menos poético 'quotiënt' en holandés moderno.

Otros términos no llegaron al holandés matemático moderno, como 'teerling' (morir, aunque todavía se usa en el sentido de morir), en lugar de cubo. Sus libros fueron best-sellers.

Curiosidades

• La asociación de estudio de ingeniería mecánica en el Technische Universiteit Eindhoven, W.S.V. Simon Stevin, es nombrado por Simon Stevin. En la memoria de Stevin, la asociación llama a su bar "De Weeghconst" y posee una flota autoconstruida de yates terrestres.
• Stevin, citado como Stevinus, es uno de los autores favoritos – si no el autor favorito: del tío Toby Shandy en Laurence Sterne La vida y las opiniones de Tristram Shandy Gentleman.
• Cita: Un hombre en enojo no es un astuto.
• En Brujas hay una plaza Simon Stevin que sostiene una estatua de Stevin hecha por Eugène Simonis. La estatua incorpora el diagrama de plano inclinado de Stevin.
• Operando desde el puerto de Ostend es un barco de reconocimiento RV Simon Stevin llamado por él.

Publicaciones

Las fortificaciones Moers diseñadas por Simon Stevin.

Entre otros, publicó:

• Tafelen van Interest (Tablas de interés) en 1582 con problemas de valor actual de cuadros de interés e interés simples y compuestos que anteriormente habían sido inéditos por los banqueros;
• Problemata geométricaa en 1583;
• De Thiende ()La Disme, La décima) en 1585 en la que se introdujeron decimales en Europa;
• La pratique d'arithmétique en 1585;
• L'arithmétique en 1585 en el que presentó un tratamiento uniforme para resolver ecuaciones algebraicas;
• Dialectike ofte bewysconst (Diáctica, o Arte de Demostración) en 1585 en Leyden por Christoffel Plantijn. Publicado de nuevo en 1621 en Rotterdam por Jan van Waesberge de Jonge.
• De Beghinselen Der Weeghconst en 1586, acompañado De Weeghdaet;
• De Beghinselen des Waterwichts (Principios sobre el peso del agua) en 1586 sobre el tema de la hidrostática;
• Vita Politica. Nombre Burgherlick leven (Vida civil) en 1590;
• De Stercktenbouwing (La construcción de fortificaciones) publicada en 1594;
• De Havenvinding (Position finding) publicado en 1599;
• De Hemelloop en 1608 en el que expresó apoyo a la teoría del Copérnico.
• In Wiskonstighe Ghedachtenissen (Memoirs Matemáticos, latín: Hypomnemata Mathematica) de 1605 a 1608. Esto incluía obras anteriores de Simon Stevin como De Driehouckhandel (Trigonometría), De Meetdaet (Práctica de medición), y Deursichtighe (Perspectiva), que editó y publicó.
• Castrametatio, dat es legermeting y Nieuwe Maniere van Stercktebou door Spilsluysen (Nuevas formas de construcción de esclusas) publicadas en 1617;
• De Spiegheling der Singconst (Teoría del arte del canto).
• "Ovares mathématiques..., Leiden, 1634