Simetría de reflexión

En matemáticas, simetría de reflexión, simetría de línea, simetría de espejo o simetría de imagen de espejo es simetría. con respecto a una reflexión. Es decir, una figura que no cambia al sufrir una reflexión tiene simetría reflexiva.

En 2D hay un eje de simetría, en 3D un plano de simetría. Un objeto o figura que es indistinguible de su imagen transformada se llama espejo simétrico. En conclusión, un eje de simetría divide la forma por la mitad y esas mitades deberían ser idénticas.

Función simétrica

En términos formales, un objeto matemático es simétrico con respecto a una operación dada como reflexión, rotación o traslación, si, cuando se aplica al objeto, esta operación preserva alguna propiedad del objeto. El conjunto de operaciones que preservan una determinada propiedad del objeto forman un grupo. Dos objetos son simétricos entre sí con respecto a un grupo dado de operaciones si uno se obtiene del otro mediante alguna de las operaciones (y viceversa).

La función simétrica de una figura bidimensional es una recta tal que, para cada perpendicular construida, si la perpendicular cruza la figura a una distancia 'd' desde el eje a lo largo de la perpendicular, entonces existe otra intersección de la forma y la perpendicular, a la misma distancia 'd' desde el eje, en dirección opuesta a lo largo de la perpendicular.

Otra forma de pensar en la función simétrica es que si la forma se doblara por la mitad sobre el eje, las dos mitades serían idénticas: las dos mitades son imágenes especulares de la otra.

Por lo tanto, un cuadrado tiene cuatro ejes de simetría, porque hay cuatro formas diferentes de doblarlo y hacer que todos los bordes coincidan. Un círculo tiene infinitos ejes de simetría.

Formas geométricas simétricas

2D formas w / simetría reflexiva

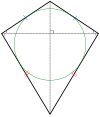isosceles trapezoid and kite
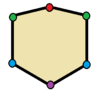Hexagons
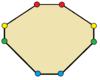octagones

Los triángulos con simetría de reflexión son isósceles. Los cuadriláteros con simetría de reflexión son cometas, deltoides (cóncavos), rombos y trapecios isósceles. Todos los polígonos de lados pares tienen dos formas reflectantes simples, una con líneas de reflejos a través de los vértices y otra a través de los bordes.

Para una forma arbitraria, la axialidad de la forma mide qué tan cerca está de ser bilateralmente simétrica. Es igual a 1 para formas con simetría de reflexión y entre 2/3 y 1 para cualquier forma convexa.

Tipos avanzados de simetría de reflexión

Para tipos de reflexión más generales, existen correspondientemente tipos más generales de simetría de reflexión. Por ejemplo:

• con respecto a una involución afina no isométrica (una reflexión oblicua en una línea, plano, etc.)
• con respecto a la inversión del círculo.

En la naturaleza

Los animales que son simétricos bilateralmente tienen simetría de reflexión en el plano sagital, que divide el cuerpo verticalmente en mitades izquierda y derecha, con uno de cada par de órganos sensoriales y extremidades a cada lado. La mayoría de los animales son bilateralmente simétricos, probablemente porque esto favorece el movimiento hacia adelante y la racionalización.

En arquitectura

La simetría espejo se utiliza a menudo en la arquitectura, como en la fachada de Santa Maria Novella, Florencia. También se encuentra en el diseño de estructuras antiguas como Stonehenge. La simetría era un elemento central en algunos estilos de arquitectura, como el Palladianismo.