Símbolo Levi-Civita

Ajustar Compartir Imprimir Citar

Antisymmetric permutation object acting on tensors

En matemáticas, particularmente en álgebra lineal, análisis de tensores y geometría diferencial, el símbolo de Levi-Civita o Levi-Civita epsilon representa una colección de números; definido a partir del signo de una permutación de los números naturales $1, 2,..., n$ , para algún entero positivo $n$ . Lleva el nombre del matemático y físico italiano Tullio Levi-Civita. Otros nombres incluyen el símbolo de permutación, símbolo antisimétrico o símbolo alterno, que se refieren a su propiedad antisimétrica y definición en términos de permutaciones.

Las letras estándar para denotar el símbolo de Levi-Civita son las minúsculas griegas épsilon $ε$ o $ϵ$ , o menos comúnmente la minúscula latina $e$ . La notación de índice permite mostrar las permutaciones de una manera compatible con el análisis tensorial:

{displaystyle varepsilon _{i_{1}i_{2}dots i_{n}}}

cada uno

i 1, i 2,... i n

1, 2,... n

n n

ε i 1 i 2 ... i n

n

anticipo total

{displaystyle varepsilon _{dots i_{p}dots i_{q}dots }=-varepsilon _{dots i_{q}dots i_{p}dots }.}

Si dos índices cualesquiera son iguales, el símbolo es cero. Cuando todos los índices son desiguales, tenemos:

{displaystyle varepsilon _{i_{1}i_{2}dots i_{n}}=(-1)^{p}varepsilon _{1,2,dots n},}

p

i 1, i 2,... i n

1, 2,... n

(1)- p

ε 1 2... n

ε 1 2... n = +1

El término " $n$ -dimensional símbolo Levi-Civita" se refiere al hecho de que el número de índices en el símbolo $n$ coincide con la dimensionalidad del espacio vectorial en cuestión, que puede ser Euclidean o no-Euclidean, por ejemplo, $mathbb {R} ^{3}$ o espacio Minkowski. Los valores del símbolo Levi-Civita son independientes de cualquier tensor métrico y sistema de coordenadas. Además, el término específico "símbolo" enfatiza que no es un tensor debido a cómo se transforma entre sistemas de coordenadas; sin embargo, puede ser interpretado como una densidad de tensor.

El símbolo de Levi-Civita permite que el determinante de una matriz cuadrada y el producto vectorial de dos vectores en el espacio euclidiano tridimensional se expresen en notación de índice de Einstein.

Definición

El símbolo de Levi-Civita se usa con mayor frecuencia en tres y cuatro dimensiones, y hasta cierto punto en dos dimensiones, por lo que se dan aquí antes de definir el caso general.

Dos dimensiones

En dos dimensiones, el símbolo de Levi-Civita se define por:

{displaystyle varepsilon _{ij}={begin{cases}+1&{text{if }}(i,j)=(1,2)\-1&{text{if }}(i,j)=(2,1)\;;,0&{text{if }}i=jend{cases}}}

{displaystyle {begin{pmatrix}varepsilon _{11}&varepsilon _{12}\varepsilon _{21}&varepsilon _{22}end{pmatrix}}={begin{pmatrix}0&1\-1&0end{pmatrix}}}

El uso del símbolo bidimensional es común en la materia condensada y en ciertos temas especializados de alta energía como la supersimetría y la teoría del twistor, donde aparece en el contexto de 2-espinores.

Tres dimensiones

Para los índices

() i, j, k)

dentro

ε ijk

, los valores

1, 2, 3

en el Orden cíclica

(1, 2, 3)

corresponde a

ε = +1

, mientras que ocurre en orden cíclico inverso corresponde a

ε = 1 -

, de lo contrario

ε = 0

En tres dimensiones, el símbolo de Levi-Civita se define por:

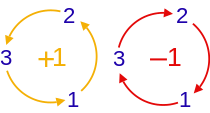
{displaystyle varepsilon _{ijk}={begin{cases}+1&{text{if }}(i,j,k){text{ is }}(1,2,3),(2,3,1),{text{ or }}(3,1,2),\-1&{text{if }}(i,j,k){text{ is }}(3,2,1),(1,3,2),{text{ or }}(2,1,3),\;;,0&{text{if }}i=j,{text{ or }}j=k,{text{ or }}k=iend{cases}}}

Es decir, $ε ijk$ es $1$ si $(i, j, k)$ es una permutación par de $(1, 2, 3)$ , $-1$ si es una permutación impar y 0 si se repite algún índice. Solo en tres dimensiones, las permutaciones cíclicas de $(1, 2, 3)$ son todas permutaciones pares, de manera similar, las permutaciones anticíclicas son todas permutaciones impares. Esto significa que en 3D es suficiente tomar permutaciones cíclicas o anticíclicas de $(1, 2, 3)$ y obtener fácilmente todas las permutaciones pares o impares.

Al igual que las matrices bidimensionales, los valores del símbolo Levi-Civita tridimensional se pueden organizar en una matriz 3 × 3 × 3:

donde $i$ es la profundidad (blue: $i = 1$ ; rojo: $i = 2$ ; verde: $i = 3$ ), $j$ es la fila y $k$ es la columna.

Algunos ejemplos:

{displaystyle {begin{aligned}varepsilon _{color {BrickRed}{1}color {Violet}{3}color {Orange}{2}}=-varepsilon _{color {BrickRed}{1}color {Orange}{2}color {Violet}{3}}&=-1\varepsilon _{color {Violet}{3}color {BrickRed}{1}color {Orange}{2}}=-varepsilon _{color {Orange}{2}color {BrickRed}{1}color {Violet}{3}}&=-(-varepsilon _{color {BrickRed}{1}color {Orange}{2}color {Violet}{3}})=1\varepsilon _{color {Orange}{2}color {Violet}{3}color {BrickRed}{1}}=-varepsilon _{color {BrickRed}{1}color {Violet}{3}color {Orange}{2}}&=-(-varepsilon _{color {BrickRed}{1}color {Orange}{2}color {Violet}{3}})=1\varepsilon _{color {Orange}{2}color {Violet}{3}color {Orange}{2}}=-varepsilon _{color {Orange}{2}color {Violet}{3}color {Orange}{2}}&=0end{aligned}}}

Cuatro dimensiones

En cuatro dimensiones, el símbolo de Levi-Civita se define por:

{displaystyle varepsilon _{ijkl}={begin{cases}+1&{text{if }}(i,j,k,l){text{ is an even permutation of }}(1,2,3,4)\-1&{text{if }}(i,j,k,l){text{ is an odd permutation of }}(1,2,3,4)\;;,0&{text{otherwise}}end{cases}}}

Estos valores se pueden organizar en una matriz 4 × 4 × 4 × 4, aunque en 4 dimensiones y más es difícil de dibujar.

Algunos ejemplos:

{displaystyle {begin{aligned}varepsilon _{color {BrickRed}{1}color {RedViolet}{4}color {Violet}{3}color {Orange}{color {Orange}{2}}}=-varepsilon _{color {BrickRed}{1}color {Orange}{color {Orange}{2}}color {Violet}{3}color {RedViolet}{4}}&=-1\varepsilon _{color {Orange}{color {Orange}{2}}color {BrickRed}{1}color {Violet}{3}color {RedViolet}{4}}=-varepsilon _{color {BrickRed}{1}color {Orange}{color {Orange}{2}}color {Violet}{3}color {RedViolet}{4}}&=-1\varepsilon _{color {RedViolet}{4}color {Violet}{3}color {Orange}{color {Orange}{2}}color {BrickRed}{1}}=-varepsilon _{color {BrickRed}{1}color {Violet}{3}color {Orange}{color {Orange}{2}}color {RedViolet}{4}}&=-(-varepsilon _{color {BrickRed}{1}color {Orange}{color {Orange}{2}}color {Violet}{3}color {RedViolet}{4}})=1\varepsilon _{color {Violet}{3}color {Orange}{color {Orange}{2}}color {RedViolet}{4}color {Violet}{3}}=-varepsilon _{color {Violet}{3}color {Orange}{color {Orange}{2}}color {RedViolet}{4}color {Violet}{3}}&=0end{aligned}}}

Generalización a n dimensiones

Más generalmente, en n dimensiones, el símbolo de Levi-Civita se define por:

{displaystyle varepsilon _{a_{1}a_{2}a_{3}ldots a_{n}}={begin{cases}+1&{text{if }}(a_{1},a_{2},a_{3},ldotsa_{n}){text{ is an even permutation of }}(1,2,3,dotsn)\-1&{text{if }}(a_{1},a_{2},a_{3},ldotsa_{n}){text{ is an odd permutation of }}(1,2,3,dotsn)\;;,0&{text{otherwise}}end{cases}}}

Por lo tanto, es el signo de la permutación en el caso de una permutación y cero en caso contrario.

Usando la notación pi mayúscula $Π$ para la multiplicación ordinaria de números, una expresión explícita para el símbolo es:

<math alttext="{displaystyle {begin{aligned}varepsilon _{a_{1}a_{2}a_{3}ldots a_{n}}&=prod _{1leq iε ε a1a2a3...... an=∏ ∏ 1≤ ≤ i.j≤ ≤ nSgn⁡ ⁡ ()aj− − ai)=Sgn⁡ ⁡ ()a2− − a1)Sgn⁡ ⁡ ()a3− − a1)⋯ ⋯ Sgn⁡ ⁡ ()an− − a1)Sgn⁡ ⁡ ()a3− − a2)Sgn⁡ ⁡ ()a4− − a2)⋯ ⋯ Sgn⁡ ⁡ ()an− − a2)⋯ ⋯ Sgn⁡ ⁡ ()an− − an− − 1){displaystyle {begin{aligned}varepsilon ##{a_{1}a_{3}ldots {cH00} {cH00} {cH00}cH00}cH00}cH00} {cH00} {cH00}cH00} {cH00FF}cH00}<img alt="{displaystyle {begin{aligned}varepsilon _{a_{1}a_{2}a_{3}ldots a_{n}}&=prod _{1leq i

Sgn

n

n = 0

n = 1

O... n 2)

O... n log(n)

Propiedades

Un tensor cuyos componentes en base ortonormal están dados por el símbolo de Levi-Civita (un tensor de rango covariante $n$ ) a veces se denomina tensor de permutación.

Bajo las reglas de transformación ordinarias para tensores, el símbolo de Levi-Civita no cambia bajo rotaciones puras, consistente con que es (por definición) el mismo en todos los sistemas de coordenadas relacionados por transformaciones ortogonales. Sin embargo, el símbolo de Levi-Civita es un pseudotensor porque bajo una transformación ortogonal del determinante jacobiano −1, por ejemplo, un reflejo en un número impar de dimensiones, debería adquirir un signo menos si fuera un tensor. Como no cambia en absoluto, el símbolo de Levi-Civita es, por definición, un pseudotensor.

Como el símbolo de Levi-Civita es un pseudotensor, el resultado de tomar un producto vectorial es un pseudovector, no un vector.

Bajo un cambio general de coordenadas, los componentes del tensor de permutación se multiplican por el jacobiano de la matriz de transformación. Esto implica que en marcos de coordenadas diferentes de aquel en el que se definió el tensor, sus componentes pueden diferir de las del símbolo de Levi-Civita por un factor global. Si el marco es ortonormal, el factor será ±1 dependiendo de si la orientación del marco es la misma o no.

En la notación tensorial sin índice, el símbolo de Levi-Civita se reemplaza por el concepto del dual de Hodge.

Los símbolos de suma se pueden eliminar usando la notación de Einstein, donde un índice repetido entre dos o más términos indica la suma sobre ese índice. Por ejemplo,

varepsilon _{ijk}varepsilon ^{imn}equiv sum _{i=1,2,3}varepsilon _{ijk}varepsilon ^{imn}

En los siguientes ejemplos, se utiliza la notación de Einstein.

Dos dimensiones

En dos dimensiones, cuando todos $i, j, m, n$ cada uno toma los valores 1 y 2:

{displaystyle varepsilon _{ij}varepsilon ^{mn}={delta _{i}}^{m}{delta _{j}}^{n}-{delta _{i}}^{n}{delta _{j}}^{m}}

()1)

{displaystyle varepsilon _{ij}varepsilon ^{in}={delta _{j}}^{n}}

()2)

{displaystyle varepsilon _{ij}varepsilon ^{ij}=2.}

()3)

Tres dimensiones

Valores de índice y símbolo

En tres dimensiones, cuando todos $i, j, k, m, n$ toman cada uno los valores 1, 2 y 3:

{displaystyle varepsilon _{ijk}varepsilon ^{pqk}=delta _{i}{}^{p}delta _{j}{}^{q}-delta _{i}{}^{q}delta _{j}{}^{p}}

()4)

{displaystyle varepsilon _{jmn}varepsilon ^{imn}=2{delta _{j}}^{i}}

()5)

varepsilon _{ijk}varepsilon ^{ijk}=6.

()6)

Producto

El símbolo de Levi-Civita está relacionado con el delta de Kronecker. En tres dimensiones, la relación viene dada por las siguientes ecuaciones (las líneas verticales indican el determinante):

{displaystyle {begin{aligned}varepsilon _{ijk}varepsilon _{lmn}&={begin{vmatrix}delta _{il}&delta _{im}&delta _{in}\delta _{jl}&delta _{jm}&delta _{jn}\delta _{kl}&delta _{km}&delta _{kn}\end{vmatrix}}\[6pt]&=delta _{il}left(delta _{jm}delta _{kn}-delta _{jn}delta _{km}right)-delta _{im}left(delta _{jl}delta _{kn}-delta _{jn}delta _{kl}right)+delta _{in}left(delta _{jl}delta _{km}-delta _{jm}delta _{kl}right).end{aligned}}}

Un caso especial de este resultado es

{displaystyle sum _{i=1}^{3}varepsilon _{ijk}varepsilon _{imn}=delta _{jm}delta _{kn}-delta _{jn}delta _{km}}

a veces denominada "identidad épsilon contratada"

En la notación de Einstein, la duplicación del índice $i$ implica la suma en $i$ . Lo anterior se denota entonces $ε ijk ε imn = δ jm δ kn - δ jn δ km$ .

{displaystyle sum _{i=1}^{3}sum _{j=1}^{3}varepsilon _{ijk}varepsilon _{ijn}=2delta _{kn}}

N dimensiones

Valores de índice y símbolo

En $n$ dimensiones, cuando todas las $i 1,..., i n, j 1,..., j n$ toma valores $1, 2,..., n$ :

{displaystyle varepsilon _{i_{1}dots i_{n}}varepsilon ^{j_{1}dots j_{n}}=delta _{i_{1}dots i_{n}}^{j_{1}dots j_{n}}}

()7)

{displaystyle varepsilon _{i_{1}dots i_{k}~i_{k+1}dots i_{n}}varepsilon ^{i_{1}dots i_{k}~j_{k+1}dots j_{n}}=delta _{i_{1}ldots i_{k}~i_{k+1}ldots i_{n}}^{i_{1}dots i_{k}~j_{k+1}ldots j_{n}}=k!~delta _{i_{k+1}dots i_{n}}^{j_{k+1}dots j_{n}}}

()8)

varepsilon _{i_{1}dots i_{n}}varepsilon ^{i_{1}dots i_{n}}=n!

()9)

donde el signo de exclamación ( $!$ ) indica el factorial y $δ α ... β ...$ es el delta de Kronecker generalizado. Para cualquier $n$ , la propiedad

{displaystyle sum _{i,j,k,dots =1}^{n}varepsilon _{ijkdots }varepsilon _{ijkdots }=n!}

se sigue de los hechos que

cada permutación es incluso o extraño,
$(+1) 2 = (1)- 2 = 1$ , y
el número de permutaciones de cualquier $n$ -element set number es exactamente $n!$ .

The particular case of (8Con ${textstyle k=n-2}$ es

{displaystyle varepsilon _{i_{1}dots i_{n-2}jk}varepsilon ^{i_{1}dots i_{n-2}lm}=(n-2)!(delta _{j}^{l}delta _{k}^{m}-delta _{j}^{m}delta _{l}^{k}),.}

Producto

En general, para $n$ dimensiones, uno puede escribir el producto de dos símbolos de Levi-Civita como:

{displaystyle varepsilon _{i_{1}i_{2}dots i_{n}}varepsilon _{j_{1}j_{2}dots j_{n}}={begin{vmatrix}delta _{i_{1}j_{1}}&delta _{i_{1}j_{2}}&dots &delta _{i_{1}j_{n}}\delta _{i_{2}j_{1}}&delta _{i_{2}j_{2}}&dots &delta _{i_{2}j_{n}}\vdots &vdots &ddots &vdots \delta _{i_{n}j_{1}}&delta _{i_{n}j_{2}}&dots &delta _{i_{n}j_{n}}\end{vmatrix}}.}

Prueba:

{displaystyle i_{1}leq cdots leq i_{n},j_{1}leq cdots leq j_{n}}

{displaystyle i_{c}=i_{c+1}}

{displaystyle j_{c}=j_{c+1}}

<math alttext="{displaystyle i_{1}<cdots <i_{n},j_{1}<cdots i1.⋯ ⋯ .in,j1.⋯ ⋯ .jn{displaystyle i_{1} - No. #<img alt="{displaystyle i_{1}<cdots <i_{n},j_{1}<cdots

Pruebas

Para (1), ambos lados son antisimétricos con respecto a $ij$ y mn. Por lo tanto, solo necesitamos considerar el caso $i \neq j$ y $m \neq n$ . Por sustitución, vemos que la ecuación se cumple para $ε 12 ε 12$ , es decir, para $i = m = 1$ y $j = n = 2$ . (Ambos lados son entonces uno). Dado que la ecuación es antisimétrica en $ij$ y $mn$ , cualquier conjunto de valores para estos se puede reducir al caso anterior (que se cumple). Por lo tanto, la ecuación se cumple para todos los valores de $ij$ y $mn$ .

Usando (1), tenemos para (2)

varepsilon _{ij}varepsilon ^{in}=delta _{i}{}^{i}delta _{j}{}^{n}-delta _{i}{}^{n}delta _{j}{}^{i}=2delta _{j}{}^{n}-delta _{j}{}^{n}=delta _{j}{}^{n},.

Aquí usamos la convención de suma de Einstein con $i$ yendo de 1 a 2. Luego, (3) se sigue de manera similar de (2).

Para establecer (5), observe que ambos lados desaparecen cuando $i \neq j$ . De hecho, si $i \neq j$ , entonces uno no puede elegir $m$ y $n$ tales que ambos símbolos de permutación a la izquierda son distintos de cero. Luego, con $i = j$ fijos, solo hay dos formas de elegir el estilo $m$ y $n$ de los dos índices restantes. Para cualquiera de estos índices, tenemos

{displaystyle varepsilon _{jmn}varepsilon ^{imn}=left(varepsilon ^{imn}right)^{2}=1}

(sin suma), y el resultado sigue.

Entonces (6) sigue desde 3! = 6 y para cualquier índice distinto $i, j, k$ tomando valores 1, 2, 3, tenemos

{displaystyle varepsilon _{ijk}varepsilon ^{ijk}=1}

(sin summation, distinct

i, j, k

)

Aplicaciones y ejemplos

Determinantes

En álgebra lineal, el determinante de una matriz cuadrada 3 × 3 $A = [a ij]$ se puede escribir

det(mathbf {A})=sum _{i=1}^{3}sum _{j=1}^{3}sum _{k=1}^{3}varepsilon _{ijk}a_{1i}a_{2j}a_{3k}

Del mismo modo, el determinante de una matriz $n \times n$ $A = [a ij]$ se puede escribir como

{displaystyle det(mathbf {A})=varepsilon _{i_{1}dots i_{n}}a_{1i_{1}}dots a_{ni_{n}},}

donde cada $i r$ debe sumarse sobre $1,..., n$ , o equivalente:

{displaystyle det(mathbf {A})={frac {1}{n!}}varepsilon _{i_{1}dots i_{n}}varepsilon _{j_{1}dots j_{n}}a_{i_{1}j_{1}}dots a_{i_{n}j_{n}},}

donde ahora cada $i r$ y cada $j r$ debe sumarse sobre $1,..., n . Más generalmente, tenemos la identidad$

{displaystyle sum _{i_{1},i_{2},dots }varepsilon _{i_{1}dots i_{n}}a_{i_{1},j_{1}}dots a_{i_{n},j_{n}}=det(mathbf {A})varepsilon _{j_{1}dots j_{n}}}

Producto cruzado vectorial

Producto cruzado (dos vectores)

Vamos ${displaystyle (mathbf {e_{1}}mathbf {e_{2}}mathbf {e_{3}})}$ una base ortonormal positivamente orientada de un espacio vectorial. Si $() a 1, a 2, a 3)$ y $() b 1, b 2, b 3)$ son las coordenadas de los vectores $a$ y $b$ en esta base, entonces su producto cruzado se puede escribir como un determinante:

mathbf {atimes b} ={begin{vmatrix}mathbf {e_{1}} &mathbf {e_{2}} &mathbf {e_{3}} \a^{1}&a^{2}&a^{3}\b^{1}&b^{2}&b^{3}\end{vmatrix}}=sum _{i=1}^{3}sum _{j=1}^{3}sum _{k=1}^{3}varepsilon _{ijk}mathbf {e} _{i}a^{j}b^{k}

Por lo tanto, también se usa el símbolo de Levi-Civita, y más simplemente:

{displaystyle (mathbf {atimes b})^{i}=sum _{j=1}^{3}sum _{k=1}^{3}varepsilon _{ijk}a^{j}b^{k}.}

En la notación de Einstein, los símbolos de suma pueden omitirse y el $i$ ésimo componente de su producto vectorial es igual a

{displaystyle (mathbf {atimes b})^{i}=varepsilon _{ijk}a^{j}b^{k}.}

El primer componente es

{displaystyle (mathbf {atimes b})^{1}=a^{2}b^{3}-a^{3}b^{2},,}

luego, mediante permutaciones cíclicas de 1, 2, 3, los demás pueden derivarse inmediatamente, sin calcularlos explícitamente a partir de las fórmulas anteriores:

{displaystyle {begin{aligned}(mathbf {atimes b})^{2}&=a^{3}b^{1}-a^{1}b^{3},,\(mathbf {atimes b})^{3}&=a^{1}b^{2}-a^{2}b^{1},.end{aligned}}}

Producto escalar triple (tres vectores)

De la expresión anterior para el producto vectorial, tenemos:

mathbf {atimes b} =-mathbf {btimes a}

Si $c = (c 1, c 2, c 3)$ es un tercer vector, entonces el triple producto escalar es igual

mathbf {a} cdot (mathbf {btimes c})=varepsilon _{ijk}a^{i}b^{j}c^{k}.

De esta expresión, se puede ver que el triple producto escalar es antisimétrico al intercambiar cualquier par de argumentos. Por ejemplo,

mathbf {a} cdot (mathbf {btimes c})=-mathbf {b} cdot (mathbf {atimes c})

Curl (un campo de vector)

Si $F = F 1, F 2, F 3)$ es un campo vectorial definido en un conjunto abierto de $mathbb {R} ^{3}$ como función de la posición $x = x 1, x 2, x 3)$ (utilizando coordenadas cartesianas). Entonces el $i$ componente del rizo $F$ iguales

{displaystyle (nabla times mathbf {F})^{i}(mathbf {x})=varepsilon _{ijk}{frac {partial }{partial x^{j}}}F^{k}(mathbf {x}),}

que se deriva de la expresión de producto cruzado anterior, sustituyendo componentes del operador de vector de gradiente (nabla).

Densidad del tensor

En cualquier sistema de coordenadas curvilíneas arbitrarias e incluso en ausencia de una métrica en la variedad, el símbolo de Levi-Civita, tal como se definió anteriormente, puede considerarse un campo de densidad tensorial de dos maneras diferentes. Puede considerarse como una densidad tensorial contravariante de peso +1 o como una densidad tensorial covariante de peso −1. En n dimensiones usando el delta de Kronecker generalizado,

{displaystyle {begin{aligned}varepsilon ^{mu _{1}dots mu _{n}}&=delta _{,1,dots ,n}^{mu _{1}dots mu _{n}},\varepsilon _{nu _{1}dots nu _{n}}&=delta _{nu _{1}dots nu _{n}}^{,1,dots ,n},.end{aligned}}}

Observe que estos son numéricamente idénticos. En particular, el signo es el mismo.

Tensores Levi-Civita

En una variedad pseudo-riemanniana, se puede definir un campo tensorial covariante invariante de coordenadas cuya representación de coordenadas concuerda con el símbolo de Levi-Civita siempre que el sistema de coordenadas sea tal que la base del espacio tangente sea ortonormal con respecto a la métrica y coincide con una orientación seleccionada. Este tensor no debe confundirse con el campo de densidad del tensor mencionado anteriormente. La presentación en esta sección sigue de cerca a Carroll 2004.

El tensor covariante de Levi-Civita (también conocido como forma de volumen de Riemann) en cualquier sistema de coordenadas que coincida con la orientación seleccionada es

{displaystyle E_{a_{1}dots a_{n}}={sqrt {left|det[g_{ab}]right|}},varepsilon _{a_{1}dots a_{n}},,}

donde $g ab$ es la representación de la métrica en ese sistema de coordenadas. De manera similar, podemos considerar un tensor de Levi-Civita contravariante elevando los índices con la métrica como de costumbre,

{displaystyle E^{a_{1}dots a_{n}}=E_{b_{1}dots b_{n}}prod _{i=1}^{n}g^{a_{i}b_{i}},,}

pero tenga en cuenta que si la firma métrica contiene un número impar de negativos $q$ , entonces el signo de los componentes de este tensor difiere del estándar Símbolo de Levi-Civita:

{displaystyle E^{a_{1}dots a_{n}}={frac {operatorname {sgn} left(det[g_{ab}]right)}{sqrt {left|det[g_{ab}]right|}}},varepsilon ^{a_{1}dots a_{n}},}

Donde $sgn(det[g ab] = (-1) q$ , y ${displaystyle varepsilon ^{a_{1}dots a_{n}}}$ es el símbolo habitual de Levi-Civita discutido en el resto de este artículo. Más explícitamente, cuando el tensor y la orientación base son elegidos tal que ${textstyle E_{01dots n}=+{sqrt {left|det[g_{ab}]right|}}}$ , tenemos eso ${displaystyle E^{01dots n}={frac {operatorname {sgn}(det[g_{ab}])}{sqrt {left|det[g_{ab}]right|}}}}$ .

De esto podemos inferir la identidad,

{displaystyle E^{mu _{1}dots mu _{p}alpha _{1}dots alpha _{n-p}}E_{mu _{1}dots mu _{p}beta _{1}dots beta _{n-p}}=(-1)^{q}p!delta _{beta _{1}dots beta _{n-p}}^{alpha _{1}dots alpha _{n-p}},,}

dónde

{displaystyle delta _{beta _{1}dots beta _{n-p}}^{alpha _{1}dots alpha _{n-p}}=(n-p)!delta _{beta _{1}}^{lbrack alpha _{1}}dots delta _{beta _{n-p}}^{alpha _{n-p}rbrack }}

es el delta de Kronecker generalizado.

Ejemplo: espacio de Minkowski

En el espacio de Minkowski (el espacio-tiempo de cuatro dimensiones de la relatividad especial), el tensor covariante de Levi-Civita es

{displaystyle E_{alpha beta gamma delta }=pm {sqrt {left|det[g_{mu nu }]right|}},varepsilon _{alpha beta gamma delta },,}

donde el signo depende de la orientación de la base. El tensor de Levi-Civita contravariante es

{displaystyle E^{alpha beta gamma delta }=g^{alpha zeta }g^{beta eta }g^{gamma theta }g^{delta iota }E_{zeta eta theta iota },.}

Los siguientes son ejemplos de la identidad general anterior especializada en el espacio de Minkowski (con el signo negativo que surge del número impar de negativos en la firma del tensor métrico en cualquiera de las convenciones de signos):

{displaystyle {begin{aligned}E_{alpha beta gamma delta }E_{rho sigma mu nu }&=-g_{alpha zeta }g_{beta eta }g_{gamma theta }g_{delta iota }delta _{rho sigma mu nu }^{zeta eta theta iota }\E^{alpha beta gamma delta }E^{rho sigma mu nu }&=-g^{alpha zeta }g^{beta eta }g^{gamma theta }g^{delta iota }delta _{zeta eta theta iota }^{rho sigma mu nu }\E^{alpha beta gamma delta }E_{alpha beta gamma delta }&=-24\E^{alpha beta gamma delta }E_{rho beta gamma delta }&=-6delta _{rho }^{alpha }\E^{alpha beta gamma delta }E_{rho sigma gamma delta }&=-2delta _{rho sigma }^{alpha beta }\E^{alpha beta gamma delta }E_{rho sigma theta delta }&=-delta _{rho sigma theta }^{alpha beta gamma },.end{aligned}}}

Símbolo Levi-Civita

Definición

Dos dimensiones

Tres dimensiones

Cuatro dimensiones

Generalización a n dimensiones

Propiedades

Dos dimensiones

Tres dimensiones

Valores de índice y símbolo

Producto

N dimensiones

Valores de índice y símbolo

Producto

Pruebas

Aplicaciones y ejemplos

Determinantes

Producto cruzado vectorial

Producto cruzado (dos vectores)

Producto escalar triple (tres vectores)

Curl (un campo de vector)

Densidad del tensor

Tensores Levi-Civita

Ejemplo: espacio de Minkowski

Número de Erdős

Roberto Boyle

Factor de eficiencia