Series geométricas

En matemáticas, una serie geométrica es la suma de un número infinito de términos que tienen una razón constante entre términos sucesivos. Por ejemplo, la serie
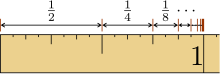
- 12+14+18+116+⋯ ⋯ {fnMicroc {fnMicroc},+,{frac {1}{4},+,{frac {1}{8}},+,{frac {1}}},+,cdots }
es geométrica, porque cada término sucesivo puede obtenerse multiplicando el término anterior por 1/2{displaystyle 1/2}. En general, una serie geométrica se escribe como a+ar+ar2+ar3+...{displaystyle a+ar+ar^{2}+ar^{3}+...}, donde a{displaystyle a} es el coeficiente de cada término y r{displaystyle r} es la relación común entre términos adyacentes. La serie geométrica tuvo un papel importante en el desarrollo temprano del cálculo, se utiliza a lo largo de las matemáticas, y puede servir como introducción a herramientas matemáticas frecuentemente usadas como la serie Taylor, la serie compleja Fourier, y la matriz exponencial.
El nombre serie geométrica indica que cada término es la media geométrica de sus dos términos vecinos, de forma similar a como el nombre serie aritmética indica que cada término es la media aritmética de sus dos términos vecinos. La secuencia de términos de series geométricas (sin ninguna de las adiciones) se denomina secuencia geométrica o progresión geométrica.
Formulación
Coeficiente a
La serie geométrica a + ar + ar2 + ar3 +... se escribe en forma desarrollada. Todos los coeficientes de la serie geométrica son iguales. Por el contrario, la serie de potencias escrita como a0 + a1r + a2r2 + a3r3 +... en forma desarrollada tiene coeficientes ai que pueden variar de un término a otro. En otras palabras, la serie geométrica es un caso especial de la serie de potencias. El primer término de una serie geométrica en forma desarrollada es el coeficiente a de esa serie geométrica.
Además de la forma desarrollada de la serie geométrica, existe una forma generadora de la serie geométrica escrita como
- .. k=0JUEGO JUEGO ark{displaystyle sum _{k=0} {infty}ar^{k}
y una forma cerrada de la serie geométrica escrita como
- <math alttext="{displaystyle {frac {a}{1-r}}{text{ for }}|r|a1− − rparaSilenciorSilencio.1.{displaystyle {frac {f}{text{ for }Principi}Principalmente, no lo sé.<img alt="{displaystyle {frac {a}{1-r}}{text{ for }}|r|
La derivación de la forma cerrada de la forma expandida se muestra en la sección § Suma de este artículo. Sin embargo, incluso sin esa derivación, el resultado se puede confirmar con una división larga: a dividido por (1 - r) da como resultado a + ar + ar2 + ar3 +... que es la forma expandida de la serie geométrica.
A menudo es conveniente en la notación establecer la serie igual a la suma s y trabajar con la serie geométrica
- s = a + ar + ar2 + ar3 + ar4 +... en su forma normalizada
- s / a = 1 + r + r2 + r3 + r4 +... o en su forma vectorial normalizada
- s / a [1 1 1 1 1...][1] r r2 r3 r4...]T o en su forma de serie parcial normalizada
- sn / a = 1 + r + r2 + r3 + r4 +... + rn, donde n es el poder (o grado) del último término incluido en la suma parcial sn.
Cambiar incluso uno de los coeficientes a algo que no sea el coeficiente a cambiaría la suma de funciones resultante a alguna función que no sea a / (1 − r ) dentro del rango |r| < 1. Como comentario aparte, la serie de Taylor define un cambio particularmente útil en los coeficientes, que describe cómo cambiar los coeficientes para que la suma de funciones converja a cualquier función seleccionada por el usuario, lo suficientemente suave dentro de un rango.
Proporción común r
La serie geométrica a + ar + ar2 + ar3 +... es una serie infinita definida por solo dos parámetros: coeficiente a y razón común r. Razón común r es la razón de cualquier término con el anterior de la serie. O, de manera equivalente, la razón común r es el término multiplicador que se usa para calcular el siguiente término de la serie. La siguiente tabla muestra varias series geométricas:
| a | r | Serie de ejemplos |
|---|---|---|
| 4 | 10 | 4 + 40 + 400 + 4000 + 40.000 + ··· |
| 3 | 1 | 3 + 3 + 3 + 3 + 3 + + ··· |
| 1 | 2/3 | 1 + 2/3 + 4/9 + 8/27 + 16/81 + ··· |
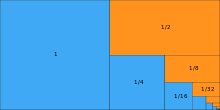
| 1/2 | 1/2 | 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ··· |
| 9 | 1/3 | 9 + 3 + 1 + 1/3 + 1/9 + ··· |
| 7 | 1/10 | 7 + 0,7 + 0,07 + 0,007 + 0,0007 +··· |
| 1 | 1/2− | 1 − 1/2 + 1/4 − 1/8 + 1/16 − 1/32 + ·· |
| 3 | −1 | 3 − 3 − 3 + 3 − 3 − ·· |
La convergencia de la serie geométrica depende del valor de la razón común r:
- Si viviéramosrTENIDO 1, los términos del enfoque de la serie cero en el límite (que se vuelve más pequeño y menor en magnitud), y la serie converge a la suma a / (1 - r).
- Si viviéramosrtención = 1, la serie no converge. Cuando r = 1, todos los términos de la serie son iguales y la serie es infinita. Cuando r = −1, los términos toman dos valores alternativamente (por ejemplo, 2, −2, 2, −2, 2,...). La suma de los términos oscila entre dos valores (por ejemplo, 2, 0, 2, 0, 2,...). Este es un tipo diferente de divergencia. Vea por ejemplo la serie Grandi: 1 − 1 + 1 − 1 + ···.
- Si viviéramosrLos términos de la serie se vuelven más grandes y más grandes en magnitud. La suma de los términos también se hace más grande y más grande, y la serie no converge a una suma. (La serie se sumerge.)
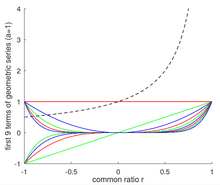
La tasa de convergencia también depende del valor de la razón común r. Específicamente, la tasa de convergencia se vuelve más lenta a medida que r se acerca a 1 o −1. Por ejemplo, la serie geométrica con a = 1 es 1 + r + r2 + r 3 +... y converge a 1 / (1 - r) cuando |r| < 1. Sin embargo, el número de términos necesarios para converger tiende a infinito cuando r tiende a 1 porque a / (1 - r) tiende a infinito y cada término de la serie es menor o igual a uno. Por el contrario, a medida que r se aproxima a −1, la suma de los primeros términos de la serie geométrica comienza a converger a 1/2, pero sube o baja ligeramente dependiendo de si el término agregado más recientemente tiene una potencia de r que es par o impar. Ese comportamiento de inversión cerca de r = −1 se ilustra en la imagen adyacente que muestra los primeros 11 términos de la serie geométrica con a = 1 y |r| < 1.
La razón común r y el coeficiente a también definen la progresión geométrica, que es una lista de los términos de la serie geométrica pero sin las adiciones. Por lo tanto la serie geométrica a + ar + ar2 + ar 3 +... tiene la progresión geométrica (también llamada secuencia geométrica) a, ar, ar2 , ar3,... La progresión geométrica, tan simple como es, modela una cantidad sorprendente de fenómenos naturales,
- de algunas de las observaciones más grandes como la expansión del universo donde la relación común r se define por la constante de Hubble,
- a algunas de las observaciones más pequeñas, como la desintegración de átomos radiactivos de carbono-14, donde la relación común r se define por la media vida del carbono-14.
Aparte, la razón común r puede ser un número complejo como |r|eiθ donde |r| es la magnitud (o longitud) del vector, θ es el ángulo (u orientación) del vector en el plano complejo e i2 = -1. Con una razón común |r|eiθ, la forma desarrollada de la serie geométrica es a + a|r|eiθ + a|r|2ei2θ + a|r| 3ei3θ +... Modelado del ángulo θ como un aumento lineal con el tiempo a razón de alguna frecuencia angular ω0 (en otras palabras, haciendo la sustitución θ = ω0t), la forma expandida de la serie geométrica se convierte en a + a|r|eiω0t + a|r|2ei2ω0t + a|r |3ei3ω0t +... donde el primer término es un vector de longitud a que no gira en absoluto, y todos los demás términos son vectores de diferentes longitudes que giran en armónicos de la frecuencia angular fundamental ω0. La restricción |r|<1 es suficiente para coordinar este número infinito de vectores de diferentes longitudes, todos girando a diferentes velocidades para trazar un círculo, como se muestra en el video adyacente. De manera similar a cómo la serie de Taylor describe cómo cambiar los coeficientes para que la serie converja a una función suficientemente suave seleccionada por el usuario dentro de un rango, la serie de Fourier describe cómo cambiar los coeficientes (que también pueden ser números complejos para especificar los ángulos iniciales). de vectores) para que la serie converja a una función periódica seleccionada por el usuario.
Suma

La suma de los primeros n términos de una serie geométrica, hasta el término r n-1 incluido, viene dada por la fórmula de forma cerrada:
donde r es la proporción común. Se puede derivar esa fórmula de forma cerrada para la suma parcial, sn, restando los muchos términos autosimilares de la siguiente manera:
A medida que n se acerca al infinito, el valor absoluto de r debe ser menor que uno para que la serie converja. La suma entonces se convierte en
La fórmula también es válida para r complejos, con la restricción correspondiente de que el módulo de r es estrictamente menor que uno.
Aparte, la pregunta de si una serie infinita converge es fundamentalmente una pregunta sobre la distancia entre dos valores: dados suficientes términos, ¿el valor de la suma parcial se acerca arbitrariamente al valor finito al que se aproxima? En la derivación anterior de la forma cerrada de la serie geométrica, la interpretación de la distancia entre dos valores es la distancia entre sus ubicaciones en la recta numérica. Esa es la interpretación más común de la distancia entre dos valores. Sin embargo, la métrica p-ádica, que se ha convertido en una noción crítica en la teoría de números moderna, ofrece una definición de distancia tal que la serie geométrica 1 + 2 + 4 + 8 +... con a = 1 y r = 2 en realidad convergen a a / (1 - r) = 1 / (1 - 2) = -1 aunque r está fuera del rango de convergencia típico |r| < 1.
Prueba de convergencia
Podemos probar que la serie geométrica converge usando la fórmula de suma para una progresión geométrica:
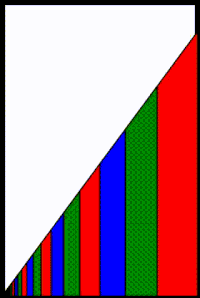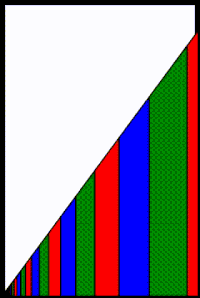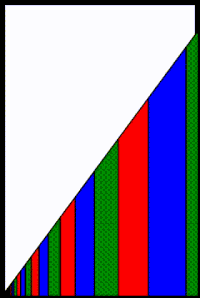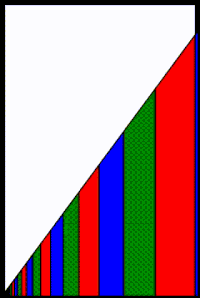
Como alternativa, en el diagrama adyacente se muestra una interpretación geométrica de la convergencia. El área del triángulo blanco es el resto de la serie = s − sn = arn+1 / (1 − r). Cada término adicional en la serie parcial reduce el área del resto del triángulo blanco por el área del trapezoide que representa el término agregado. Las áreas trapezoidales (es decir, los valores de los términos) se vuelven progresivamente más delgadas, más cortas y más cercanas al origen. En el límite, a medida que el número de trapecios se aproxima a infinito, el resto del triángulo blanco se desvanece cuando se llena de trapecios y, por lo tanto, sn converge en s, siempre que |r|<1. Por el contrario, si |r|>1, las áreas trapezoidales que representan los términos de la serie se vuelven progresivamente más anchas, más altas y más alejadas del origen, sin converger al origen y sin converger como una serie.
Tasa de convergencia
Después de saber que una serie converge, hay algunas aplicaciones en las que también es importante saber qué tan rápido converge la serie. Para la serie geométrica, una medida conveniente de la tasa de convergencia es cuánto disminuye el resto de la serie anterior debido al último término de la serie parcial. Dado que el último término es arn y el resto de la serie anterior es s - sn- 1 = arn / (1 - r)), esta medida de la tasa de convergencia de la serie geométrica es arn / (arn / (1 - r)) = 1 - r, si 0 ≤ r < 1.
Si r < 0, los términos adyacentes en la serie geométrica alternan entre ser positivos y negativos. Una interpretación geométrica de una serie geométrica alterna convergente se muestra en el diagrama adyacente en el que las áreas de los términos negativos se muestran debajo del eje x. Emparejar y sumar cada área positiva con su vecina de área más pequeña negativa da como resultado trapecios no superpuestos separados por espacios. Para eliminar los espacios, ensancha cada trapecio para cubrir el 1 - r2 más a la derecha del área del triángulo original en lugar de solo el 1 - |r más a la derecha >|. Sin embargo, para mantener las mismas áreas trapezoidales durante esta transformación de ampliación, se necesita escalar: scale*(1 - r2) = (1 - |r|), o escala = (1 - |r|) / (1 - r2) = (1 + r) / (1 - r2) = (1 + r) / ((1 + r)(1 - r)) = 1 / (1 - r) donde -1 < r ≤ 0. Tenga en cuenta que debido a que r < 0 esta escala disminuye la amplitud de los trapecios separados para llenar los huecos de separación. Por el contrario, para el caso r > 0 la misma escala 1 / (1 - r) aumenta la amplitud de los trapecios no superpuestos para tener en cuenta la pérdida de las áreas superpuestas.
Con los espacios eliminados, los pares de términos en una serie geométrica alterna convergente se convierten en una serie geométrica convergente (no alterna) con una razón común r2 para dar cuenta de la emparejamiento de términos, coeficiente a = 1 / (1 - r) para tener en cuenta el relleno del hueco, y el grado (es decir, el término de mayor potencia) de la serie parcial llamada m en lugar de n para enfatizar que los términos se han emparejado. Similar a r > 0 caso, el r < 0 tasa de convergencia = ar2m / (s - sm-1) = 1 - r 2, que es igual a la tasa de convergencia de una serie geométrica no alterna si sus términos estuvieran emparejados de manera similar. Por lo tanto, la tasa de convergencia no depende de n o my, lo que quizás sea más sorprendente, no depende del signo de la razón común. Una perspectiva que ayuda a explicar la tasa variable de convergencia que es simétrica con respecto a r = 0 es que cada término agregado de la serie parcial hace una contribución finita a la suma infinita en r = 1 y cada término sumado de la serie parcial hace una contribución finita a la pendiente infinita en r = -1.
Derivación
Series finitas
Para derivar esta fórmula, primero escribe una serie geométrica general como:
Podemos encontrar una fórmula más simple para esta suma multiplicando ambos lados de la ecuación anterior por 1 − r, y veremos que
ya que todos los demás términos se cancelan. Si r ≠ 1, podemos reorganizar lo anterior para obtener la fórmula conveniente para una serie geométrica que calcula la suma de n términos:
- Fórmulas relacionadas
Si uno comenzara la suma no de k=1 o 0 sino de un valor diferente, digamos m{displaystyle m}, entonces
Diferenciando esta fórmula con respecto a r{displaystyle r} nos permite llegar a fórmulas por sumas de la forma
Por ejemplo:
Para una serie geométrica que contiene sólo poderes de r{displaystyle r} multiplicado por 1− − r2{displaystyle 1-r^{2}:
Equivalentemente, toma r2{displaystyle r^{2} como la relación común y utilizar la formulación estándar.
Para una serie con sólo poderes extraños r{displaystyle r},
Una fórmula exacta para la suma generalizada Gs()n,r){displaystyle G_{s}(n,r)} cuando s▪ ▪ N{displaystyle sin mathbb {N} se expande por los números Stirling del segundo tipo como
Serie infinita
Una serie geométrica infinita es una serie infinita cuyos términos sucesivos tienen una razón común. Tal serie converge si y solo si el valor absoluto de la razón común es menor que uno (| r| < 1). Su valor se puede calcular a partir de la fórmula de suma finita
Desde:
Entonces:
Para una serie que contiene sólo poderes de r{displaystyle r},
En los casos en que la suma no comienza en k = 0,
Esta fórmula solo funciona para |r| < 1 también De esto se deduce que, para |r| < 1,
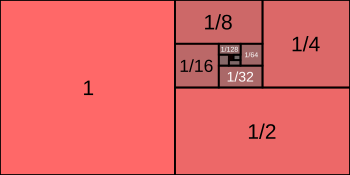
Además, la serie infinita 1/2 + 1/4 + 1/8 + 1/16 + ⋯ es un ejemplo elemental de una serie que converge absolutamente.
Es una serie geométrica cuyo primer término es 1/2 y cuya razón común es 1/2, por lo que su suma es
El inverso de la serie anterior es 1/2 − 1/4 + 1/8 − 1/16 + ⋯ es un ejemplo simple de una serie alterna que converge absolutamente.
Es una serie geométrica cuyo primer término es 1/2 y cuya razón común es −1/2, por lo que su suma es
Serie compleja
La fórmula de suma para series geométricas sigue siendo válida incluso cuando la razón común es un número complejo. En este caso, la condición de que el valor absoluto de r sea menor que 1 se convierte en que el módulo de r sea menor que 1. Es posible calcular las sumas de algunos no -series geométricas obvias. Por ejemplo, considere la proposición
La prueba de esto viene del hecho de que
Esta es la diferencia de dos series geométricas, por lo que es una aplicación sencilla de la fórmula para series geométricas infinitas que completa la demostración.
Historia
Zeno de Elea (c. 495 - c. 430 a. C.)
Hace 2500 años, los matemáticos griegos tenían un problema al caminar de un lugar a otro: pensaban que una lista infinitamente larga de números mayores que cero sumaban infinito. Por eso, fue una paradoja cuando Zenón de Elea señaló que para caminar de un lugar a otro, primero hay que caminar la mitad de la distancia, y luego hay que caminar la mitad de la distancia restante, y luego hay que caminar la mitad de esa distancia restante, y continúas reduciendo a la mitad las distancias restantes un número infinito de veces porque no importa cuán pequeña sea la distancia restante, todavía tienes que caminar la primera mitad. Así, Zeno de Elea transformó una distancia corta en una lista infinitamente larga de distancias restantes reducidas a la mitad, todas las cuales son mayores que cero. Y ese era el problema: ¿cómo puede una distancia ser corta cuando se mide directamente y también infinita cuando se suma sobre su lista infinita de residuos reducidos a la mitad? La paradoja reveló que algo andaba mal con la suposición de que una lista infinitamente larga de números mayores que cero sumaban infinito.
Euclides de Alejandría (c. 300 a. C.)
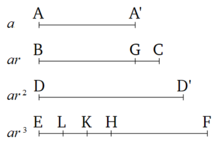
Elementos de Geometría de Euclides Libro IX, Proposición 35, prueba (de la proposición en el título del diagrama adyacente):
Que AA', BC, DD', EF sea cualquier multitud de números continuamente proporcionales, comenzando desde el menos A'. Y que BG y FH, cada uno igual a A', han sido restados de BC y EF. Digo que como GC es para AA', así que EH es para A', BC, DD'.
Para que FK sea igual a BC, y FL a DD'. Y dado que FK es igual a BC, de los cuales FH es igual a BG, el HK restante es así igual al GC restante. Y como EF es para DD', así DD' a BC, y BC a AA' [Prop. 7.13], y DD' igual a FL, y BC a FK, y AA' a FH, así como EF es a FL, así LF a FK, y FK a FH. Por separación, como EL a LF, así LK a FK, y KH a FH [Props. 7.11, 7.13]. Y así como uno de los principales es a uno de los siguientes, así (la suma de) todos los que conducen a (la suma de) todos los siguientes [Prop. 7.12]. Así, como KH es para FH, así que EL, LK, KH a LF, FK, HF. Y KH igual a CG, y FH a A', y LF, FK, HF a DD', BC, AA'. Así, como CG es para A', así que EH a D', BC, AA'. Así, como el exceso del segundo es al primero, así es el exceso del último es para todos los que la tienen. Lo mismo que debía mostrar.
La brevedad de las proposiciones y pruebas de Euclides puede haber sido una necesidad. Tal como está, Elements of Geometry tiene más de 500 páginas de proposiciones y pruebas. Hacer copias de este popular libro de texto requería mucho trabajo dado que la imprenta no se inventó hasta 1440. Y la popularidad del libro duró mucho tiempo: como se indica en la introducción citada de una traducción al inglés, Elements of Geometry "tiene la distinción de ser el libro de texto de matemáticas en uso continuo más antiguo del mundo." Así que ser muy conciso era ser muy práctico. La prueba de la Proposición 35 en el Libro IX podría haber sido aún más compacta si Euclides hubiera podido evitar de alguna manera igualar explícitamente las longitudes de segmentos de línea específicos de diferentes términos en la serie. Por ejemplo, la notación contemporánea para series geométricas (es decir, a + ar + ar2 + ar3 +... + arn) no etiqueta porciones específicas de términos que son iguales entre sí.
También en la introducción citada, el editor comenta:
La mayoría de los teoremas apareciendo en los Elementos no fueron descubiertos por el mismo Euclides, sino que fueron obra de los antiguos matemáticos griegos como Pythagoras (y su escuela), Hipócrates de Chios, Teaeteto de Atenas, y Eudoxus de Cnidos. Sin embargo, Euclid es generalmente acreditado con la organización de estos teoremas de una manera lógica, para demostrar (admitidamente, no siempre con el rigor demandado por las matemáticas modernas) que necesariamente siguen de cinco simples axiomas. Euclid también se acredita con la idea de una serie de pruebas particularmente ingeniosas de teoremas previamente descubiertos (por ejemplo, Teorema 48 en el Libro 1).
Para ayudar a traducir la proposición y la prueba en una forma que use la notación actual, hay un par de modificaciones en el diagrama. En primer lugar, las cuatro longitudes de línea horizontal que representan los valores de los primeros cuatro términos de una serie geométrica ahora se denominan a, ar, ar2, ar3 en el diagrama's margen izquierdo. En segundo lugar, las nuevas etiquetas A' y D' ahora están en la primera y la tercera línea para que todos los nombres de segmento de línea del diagrama especifiquen consistentemente el punto de inicio y el punto final del segmento.
Aquí hay una interpretación frase por frase de la proposición:
| Proposición | notación contemporánea |
|---|---|
| "Si hay alguna multitud de números continuamente proporcionales" | Tomando los primeros n+1 términos de una serie geométrica Sn = a + ar + ar2 + ar3 +... + arn |
| "y igual al primero se resta del segundo y el último" | y subcontratación a desde ar y arn |
| "entonces como el exceso del segundo al primero, por lo que el exceso del último será para todos los que lo preceden." | entonces...ar-a) a =arn-a♪a + ar + ar2 + ar3 +... + arn-1) =arn-a)n-1, que se puede reorganizar a la forma más familiar Sn-1 = a()rn-1) / (r-1). |
Del mismo modo, aquí hay una interpretación oración por oración de la prueba:
| Prueba | notación contemporánea |
|---|---|
| "Que AA', BC, DD', EF sea cualquier multitud de números continuamente proporcionales, comenzando desde el menos AA'." | Considere los primeros n+1 términos de una serie geométrica Sn = a + ar + ar2 + ar3 +... + arn para el caso rØ1 y n=3. |
| "Y que BG y FH, cada uno igual a AA', hayan sido restados de BC y EF." | Subtract a desde ar y ar3. |
| "Yo digo que como GC es para AA', así que EH es para A', BC, DD'." | Yo digo eso.ar-a) a =ar3-a♪a + ar + ar2). |
| "Por que FK sea igual a BC y FL a DD". | |
| "Y como FK es igual a BC, de la cual FH es igual a BG, el HK restante es así igual al GC restante." | |
| "Y como EF es para DD', así DD' a BC, y BC a AA' [Prop. 7.13], y DD' igual a FL, y BC a FK, y AA' a FH, así como EF es a FL, así LF a FK, y FK a FH." | |
| "Por separación, como EL a LF, así LK a FK, y KH a FH [Props. 7.11, 7.13]." | Por separación (ar3-ar2) ar2 =ar2-ar) ar =ar-a) a = r-1. |
| "Y así como uno de los principales es a uno de los siguientes, así (la suma de) todo lo que conduce a (la suma de) todo lo siguiente [Prop. 7.12]." | La suma de esos numeradores y la suma de esos denominadores forman la misma proporción: ((ar3-ar2) + (ar2-ar) + (ar-a) / (ar2 + ar + a) r-1. |
| "Y así como uno de los principales es a uno de los siguientes, así (la suma de) todo lo que conduce a (la suma de) todo lo siguiente [Prop. 7.12]." | Y esta suma de igual proporción puede extenderse más allá (ar3-ar2) ar2 incluir todas las proporciones hasta (arn-arn-1) arn-1. |
| "Así, como KH es para FH, así que EL, LK, KH a LF, FK, HF." | |
| "Y KH igual a CG, y FH a AA', y LF, FK, HF a DD', BC, AA'." | |
| "Así, como CG es para AA", así que EH a DD', BC, AA'." | |
| "Así, como el exceso del segundo es para el primero, así es el exceso del último es para todos los que lo tienen delante." | Así (ar-a) a =ar3-a)2. O más generalmente, (ar-a) a =arn-a)n-1, que se puede reorganizar en la forma más común Sn-1 = a()rn-1) / (r-1). |
| "Lo mismo que se requería para mostrar." | Q.E.D. |
Arquímedes de Siracusa (c.287 – c.212 a. C.)
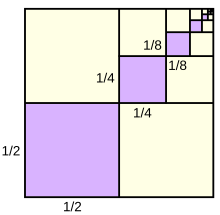
Arquímedes usó la suma de una serie geométrica para calcular el área encerrada por una parábola y una línea recta. Su método consistía en diseccionar el área en un número infinito de triángulos.
Arquímedes N.º 39; El teorema establece que el área total bajo la parábola es 4/3 del área del triángulo azul.
Arquímedes determinó que cada triángulo verde tiene 1/8 del área del triángulo azul, cada triángulo amarillo tiene 1/8 del área de un triángulo verde, y así sucesivamente.
Suponiendo que el triángulo azul tiene un área de 1, el área total es una suma infinita:
- 1+2()18)+4()18)2+8()18)3+⋯ ⋯ .{displaystyle 1,+,2left({frac {1}{8}right),+,4left({frac {1}{8}}}right)^{2},+,8left({frac {1}{8}}}}}derecha)},+,cdots}.
El primer término representa el área del triángulo azul, el segundo término las áreas de los dos triángulos verdes, el tercer término las áreas de los cuatro triángulos amarillos y así sucesivamente. Simplificando las fracciones da
- 1+14+116+164+⋯ ⋯ .{displaystyle 1,+,{frac {1}{4},+,{16},+,{frac {1}{64},+,cdots.}
Esta es una serie geométrica con razón común 1/4 y la parte fraccionaria es igual a
- .. n=0JUEGO JUEGO 4− − n=1+4− − 1+4− − 2+4− − 3+⋯ ⋯ =43.{displaystyle sum _{n=0}{infty }4^{-n}=1+4^{-1}+4^{-2}+4^{-3}+cdots ={4 over 3}
La suma es
- 11− − r=11− − 14=43.{fnMicroc} {1}{1-r};=;{frac} {1}{1-{frac {1}{4}};=;{frac} {4}{3}}
Este cálculo utiliza el método de agotamiento, una versión anterior de la integración. Usando cálculo, se podría encontrar la misma área mediante una integral definida.
Nicole Oresme (c. 1323 - 1382)
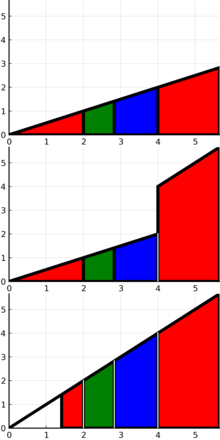
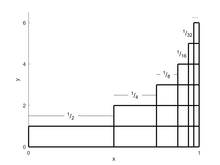
Entre sus ideas sobre las series infinitas, además de su demostración elegantemente sencilla de la divergencia de las series armónicas, Nicole Oresme demostró que la serie 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6/64 + 7/128 +... converge a 2. Su diagrama para su prueba geométrica, similar al diagrama adyacente, muestra una serie geométrica de dos dimensiones. La primera dimensión es horizontal, en la fila inferior muestra la serie geométrica S = 1/2 + 1/4 + 1/8 + 1/16 +... que es la serie geométrica con coeficiente a = 1/2 y razón común r = 1/2 que converge a S = a / (1- r) = (1/2) / (1-1/2) = 1. La segunda dimensión es vertical, donde la fila inferior es un nuevo coeficiente aT igual a S y cada fila subsiguiente por encima de ella está escalada por la misma razón común r = 1/2, haciendo otra serie geométrica T = 1 + 1/2 + 1/4 + 1/8 +..., que es la serie geométrica con coeficiente aT = S = 1 y razón común r = 1/2 que converge a T = aT / (1-r) = S / (1- r) = a / (1-r) / (1-r) = (1/2) / (1 -1/2) / (1-1/2) = 2.
Aunque es difícil de visualizar más allá de las tres dimensiones, la visión de Oresme se generaliza a cualquier dimensión d. Usar la suma de la dimensión d−1 de la serie geométrica como el coeficiente a en la dimensión d de la serie geométrica da como resultado un d-dimensional convergente a Sd / a = 1 / (1 -r)d dentro del rango |r|<1. El triángulo de Pascal y la división larga revelan los coeficientes de estas series geométricas multidimensionales, donde la forma cerrada es válida solo dentro del rango |r|<1.
- 111121133114641{displaystyle {begin{matrix}111114quad 2quad 111quad 3quad 3quad 111quad 4quad 6quad 4quad 1quad 1end{matrix}}}}}}}}}
| d{displaystyle d} | Sd{displaystyle S^{d} (forma cerrada) | Sd{displaystyle S^{d} (forma gastada) |
|---|---|---|
| 1{displaystyle 1} | 1/()1− − r){displaystyle 1/(1-r)} | 1+r+r2+r3+r4+⋯ ⋯ {displaystyle 1+r+r^{2}+r^{3}+r^{4}+cdots } |
| 2{displaystyle 2} | 1/()1− − r)2{displaystyle 1/(1-r)}{2} | 1+2r+3r2+4r3+5r4+⋯ ⋯ {displaystyle 1+2r+3r^{2}+4r^{3}+5r^{4}+cdots } |
| 3{displaystyle 3} | 1/()1− − r)3{displaystyle 1/(1-r)}{3} | 1+3r+6r2+10r3+15r4+⋯ ⋯ {displaystyle 1+3r+6r^{2}+10r^{3}+15r^{4}+cdots } |
| 4{displaystyle 4} | 1/()1− − r)4{displaystyle 1/(1-r)} {4} | 1+4r+10r2+20r3+35r4+⋯ ⋯ {displaystyle 1+4r+10r^{2}+20r^{3}+35r^{4}+cdots } |
Aparte, en lugar de usar la división larga, también es posible calcular los coeficientes de la serie geométrica d-dimensional integrando los coeficientes de dimensión d− 1. Este mapeo desde la división por 1-r en el dominio de la suma de la serie de potencias hasta la integración en el dominio del coeficiente de la serie de potencias es una forma discreta del mapeo realizado por la transformada de Laplace. El profesor del MIT, Arthur Mattuck, muestra cómo derivar la transformada de Laplace de la serie de potencias en este video de conferencia, donde la serie de potencias es un mapeo entre coeficientes discretos y una suma y la transformada de Laplace es un mapeo entre pesos continuos y una integral.
Aplicaciones
Economía
En economía, las series geométricas se utilizan para representar el valor presente de una anualidad (una suma de dinero a pagar en intervalos regulares).
Por ejemplo, supongamos que un pago de $100 se hará al propietario de la anualidad una vez al año (al final del año) en perpetuidad. Recibir $100 al año vale menos que un $100 inmediato, porque uno no puede invertir el dinero hasta que uno lo reciba. En particular, el valor actual de $100 al año en el futuro es de $100 / (1 +I{displaystyle Yo...), donde I{displaystyle Yo... es el tipo de interés anual.
Del mismo modo, un pago de $100 dos años en el futuro tiene un valor presente de $100 / (1 +I{displaystyle Yo...)2 (squared porque dos años de interés se pierde por no recibir el dinero ahora mismo). Por lo tanto, el valor actual de recibir $100 al año en perpetuidad es
- .. n=1JUEGO JUEGO $ $ 100()1+I)n,{displaystyle sum _{n=1} {infty}{frac {$100}{(1+I)^{n}}}}
que es la serie infinita:
- $ $ 100()1+I)+$ $ 100()1+I)2+$ $ 100()1+I)3+$ $ 100()1+I)4+⋯ ⋯ .{fnMicroc {$100},+,{fnMicroc {$100}{(1+I)}}},+,{\fc {$100}{(1+I)}}},+,{fc} {fnMicroc} {c}c}ccc}cc}cc}cc}cccc}cc}ccccc}cccccccccccccccccccc}cccccccccc}cccccccccccccccccccccccccccccc
Esta es una serie geométrica con relación común 1 / (1 +I{displaystyle Yo...). La suma es el primer término dividido por (uno menos la relación común):
- $ $ 100/()1+I)1− − 1/()1+I)=$ $ 100I.{displaystyle {frac {$100/(1+I)}{1-1/(1+I)};=;{frac {$100}{I}}
Por ejemplo, si el tipo de interés anual es del 10% (I{displaystyle Yo...= 0.10), entonces toda la anualidad tiene un valor presente de $100 / 0.10 = $1000.
Este tipo de cálculo se utiliza para calcular la APR de un préstamo (como un préstamo hipotecario). También se puede utilizar para estimar el valor actual de los dividendos esperados en acciones, o el valor terminal de un activo financiero suponiendo una tasa de crecimiento estable.
Geometría fractal
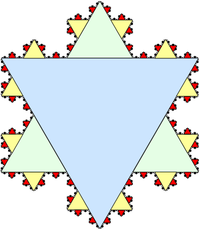
Por ejemplo, el área dentro del copo de nieve de Koch se puede describir como la unión de infinitos triángulos equiláteros (ver figura). Cada lado del triángulo verde es exactamente 1/3 del tamaño de un lado del triángulo azul grande y, por lo tanto, tiene exactamente 1/9 del área. De manera similar, cada triángulo amarillo tiene 1/9 del área de un triángulo verde, y así sucesivamente. Tomando el triángulo azul como unidad de área, el área total del copo de nieve es
- 1+3()19)+12()19)2+48()19)3+⋯ ⋯ .{displaystyle 1,+,3left({frac {1}{9}right),+,12left({frac {1}{9}}}right)^{2},+,48left({frac {1}{9}}}}}derecha),+,cdots}
El primer término de esta serie representa el área del triángulo azul, el segundo término el área total de los tres triángulos verdes, el tercer término el área total de los doce triángulos amarillos, y así sucesivamente. Excluyendo el 1 inicial, esta serie es geométrica con razón constante r = 4/9. El primer término de la serie geométrica es a = 3(1/9) = 1/3, por lo que la suma es
- 1+a1− − r=1+131− − 49=85.{displaystyle 1,+,{frac {a}{1-r};=;1,+,{frac {frac} {1}{1}{1-{frac {4}{9}};=;{frac} {8}{5}}
Por lo tanto, el copo de nieve de Koch tiene 8/5 del área del triángulo base.
Integración
El derivado de f()x)=arctan ()u()x))esf.()x)=u.()x)/()1+[u()x)]2){displaystyle f(x)=arctan(u(x){text{ is }f'(x)=u'(x)/(1+[u(x)]^{2}} porque, dejar Sí.yuRepresentaciónf()x)yu()x),{displaystyle y{text{ >}u {text{ represent }f(x){text{ > }u(x),}
- <math alttext="{displaystyle {begin{aligned}y&=arctan(u)&&quad {text{ implies }}\u&=tan(y)&&quad {text{ in the range }}-pi /2<ySí.=arctan ()u)implicaciónu=# ()Sí.)en el rango− − π π /2.Sí..π π /2yu.=sec2 Sí.⋅ ⋅ Sí..aplicando la regla del cociente# ()Sí.)=pecado ()Sí.)/# ()Sí.),Sí..=u./sec2 Sí.dividiendo ambos lados porsec2 Sí.,=u./()1+#2 Sí.)utilizando la identidad trigonométrica derivada de la divisiónpecado2 Sí.+#2 Sí.=1por#2 Sí.,=u./()1+u2)recordandou=# ()Sí.).################################################################################################################################################################################################################################################################<img alt="{displaystyle {begin{aligned}y&=arctan(u)&&quad {text{ implies }}\u&=tan(y)&&quad {text{ in the range }}-pi /2<y
Por lo tanto, dejando u()x)=x,arctan ()x){displaystyle u(x)=x,arctan(x)} es la integral
- <math alttext="{displaystyle {begin{aligned}arctan(x)&=int {frac {dx}{1+x^{2}}}quad &&{text{in the range }}-pi /2<arctan(x)arctan ()x)=∫ ∫ dx1+x2en el rango− − π π /2.arctan ()x).π π /2,=∫ ∫ dx1− − ()− − x2)por escrito integrado como forma cerrada de serie geométrica conr=− − x2,=∫ ∫ ()1+()− − x2)+()− − x2)2+()− − x2)3+⋯ ⋯ )dxpor escribir serie geométrica en forma ampliada,=∫ ∫ ()1− − x2+x4− − x6+⋯ ⋯ )dxcalculando el signo y el poder de cada término en componentes,=x− − x33+x55− − x77+⋯ ⋯ mediante la integración de cada término,=.. n=0JUEGO JUEGO ()− − 1)n2n+1x2n+1por escrito serie en forma de generador,{displaystyle {begin{aligned}arctan(x) recur=int {frac {f}{1+x^{2}}quad {text{in {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {x^{3}{3}}+{frac} {x^{5}{5}} {frac} {x^{7}}{7}+cdots quad ' Ivoire {text{by integrating each term}},\=sum _{n=0}{infty }{frac {(-1)^{n}{2n+1}x^{2n+1}quad >}{text{end}{=0}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}}}}}}{}{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}{}}}}}}}}}}}{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}<img alt="{displaystyle {begin{aligned}arctan(x)&=int {frac {dx}{1+x^{2}}}quad &&{text{in the range }}-pi /2<arctan(x)
que se denomina serie de Gregory y se atribuye comúnmente a Madhava de Sangamagrama (c. 1340 - c. 1425).
Instancias
- Serie de Grandi – La suma infinita de alternar 1 y -1 términos: 1 − 1 + 1 − 1 + ⋯
- 1 + 2 + 4 + 8 + ⋯ – Serie Infinita
- 1 − 2 + 4 - 8 + ⋯
- 1/2 + 1/4 + 1/8 + 1/16 + ⋯ – serie infinita matemática
- 1/2 − 1/4 + 1/8 − 1/16 + ⋯
- 1/4 + 1/16 + 1/64 + 1/256 + ⋯
- Una serie geométrica es una serie de unidades (la suma de la serie converge a una) si y sólo si TENrTENIDAS a + r = 1 (equivalente a la forma más familiar S = a / (1 - r) = 1 cuando.rTENIDO 1 Por lo tanto, una serie alterna es también una serie de unidades cuando -1 r 0 y a + r = 1 (por ejemplo, coeficiente a = 1,7 y ratio común r = 0,7).
- Los términos de una serie geométrica son también los términos de una secuencia generalizada de Fibonacci (Fn Fn-1 + Fn-2 pero sin necesidad F0 = 0 y F1 = 1) cuando una relación común de serie geométrica r satisfice la restricción 1 + r = r2, que según la fórmula cuadrática es cuando la relación común r iguala la relación de oro (es decir, la relación común r = (1 ± √5)/2).
- La única serie geométrica que es una serie unitaria y también tiene términos de una secuencia generalizada de Fibonacci tiene la relación de oro como su coeficiente a y la relación de oro conyugal como su relación común r (es decir, a = (1 + √5)/2 y r = (1 - √5)/2). Es una serie de unidades porque a + r = 1 y confidencialidadrTENIDO 1, es una secuencia generalizada de Fibonacci porque 1 + r = r2, y es una serie alternada porque r 0.
Serie geométrica

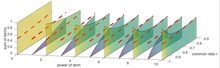
La serie geométrica tiene dos grados de libertad: uno por su coeficiente a y otro por su razón común r. En el mapa de polinomios, el gran círculo rojo representa el conjunto de todas las series geométricas.
Series geométricas convergentes
Solo converge un subconjunto de todas las series geométricas. Específicamente, una serie geométrica converge si y solo si su razón común |r| < 1. En el mapa de polinomios, el triángulo rojo representa el conjunto de series geométricas convergentes y, al dibujarse dentro del gran círculo rojo que representa el conjunto de todas las series geométricas, indica que la serie geométrica convergente es un subconjunto de la serie geométrica.
Decimales repetidos
Solo un subconjunto de todas las series geométricas convergentes convergen en fracciones decimales que tienen patrones repetidos que continúan para siempre (por ejemplo, 0,7777... o 0,9999... o 0,123412341234...). En el mapa de polinomios, el pequeño triángulo amarillo representa el conjunto de series geométricas que convergen en patrones decimales repetidos infinitamente. Se dibuja dentro del triángulo rojo para indicar que es un subconjunto de la serie geométrica convergente, que a su vez se dibuja dentro del gran círculo rojo que indica que tanto la serie geométrica convergente como la serie geométrica que converge en patrones repetidos infinitamente son subconjuntos de la serie geométrica. serie.
Aunque las fracciones con patrones decimales repetidos infinitamente solo se pueden aproximar cuando se codifican como números de punto flotante, siempre se pueden definir exactamente como la proporción de dos enteros y esos dos enteros se pueden calcular usando la serie geométrica. Por ejemplo, la fracción decimal repetida 0.7777... se puede escribir como la serie geométrica
- 0.7777...... =710+710110+7101102+7101103+⋯ ⋯ {fnMicrosoft Sans Serif} {fnMicroc} {fnMicroc} {fnMicroc {7} {} {fnMicroc} {c} {fnMicroc {7} {fnMicroc} {c} {c} {c} {fnMicroc} {c}} {c} {c} {c}}} {c}c} {c}c}c}c} {c} {c}c}c} {cccccc}ccccccccc}cccccccccc}ccccccccc}cccccc}ccc}cccccccccc
donde coeficiente a = 7/10 y razón común r = 1/10. La forma cerrada de la serie geométrica revela los dos números enteros que especifican el patrón repetido:
- 0.7777...... =a1− − r=7/101− − 1/10=7/109/10=79.{displaystyle 0.7777ldots ;=;{frac {a}{1-r};=;{frac} {7/10}{1-1/10};=;{frac {7/10}{9/10};=;{frac} {7}{9}.}
Este enfoque va más allá de los números de base diez. De hecho, cualquier fracción que tiene un patrón repetido infinitamente en números de base diez también tiene un patrón repetido infinitamente en números escritos en cualquier otra base. Por ejemplo, mirando la codificación de punto flotante para el número 0.7777...
julia> cadena de bits(Float32(0.77777777777777777777))
"00111111010001110001110001110010"
revela la fracción binaria 0.110001110001110001... donde el patrón binario 0b110001 se repite indefinidamente y se puede escribir en su mayoría (excepto las potencias) números binarios como
- 0.110001110001110001...... =1100011000000+110001100000011000000+1100011000000110000002+1100011000000110000003+⋯ ⋯ {displaystyle 0.110001110001110001ldots ;=;{frac {110001}{1000000},+,{frac {110001}{1000000}{frac {1}{1000000},+,{frac {110001}{1000000}{frac}{frac {1}{2}},+,{frac {110001}{frac}{frac} {Microc} {1}{000000000},+,cdots }
donde coeficiente a = 0b110001 / 0b1000000 = 49 / 64 y razón común r = 1 / 0b1000000 = 1 / 64. Usando la forma cerrada de la serie geométrica como antes
- 0.7777...... =0b0.110001110001110001...... =a1− − r=49/641− − 1/64=49/6463/64=4963=79.{displaystyle 0.7777ldots ;=;0b0.110001110001110001ldots ;=;{frac {a}{1-r};=;{frac} {49/64}{1-1/64};=;{frac {49/64}{63/64};=;{frac {49}{63};=;{frac} {7}{9}.}
Es posible que haya notado que la codificación de punto flotante no captura el patrón de repetición 0b110001 en los últimos bits (menos significativos). Esto se debe a que la codificación de punto flotante redondea el resto en lugar de truncarlo. Por lo tanto, si el bit más significativo del resto es 1, el bit menos significativo de la fracción codificada se incrementa y eso causará un acarreo si el bit menos significativo de la fracción ya es 1, lo que puede causar otro acarreo si ese bit de la fracción ya es un 1, lo que puede causar otro acarreo, etc. Este redondeo de punto flotante y la subsiguiente propagación del acarreo explican por qué la codificación de punto flotante para 0.99999... es exactamente la misma que la codificación de punto flotante para 1.
julia> cadena de bits(Float32(0.999999999999999999999))
"001111111000000000000000000000000"
julia> cadena de bits(Float32(1.0))
"001111111000000000000000000000000"
Como ejemplo que tiene cuatro dígitos en el patrón repetido, 0.123412341234... se puede escribir como la serie geométrica
- 0.123412341234...... =123410000+123410000110000+1234100001100002+1234100001100003+⋯ ⋯ {displaystyle 0.123412341234ldots ;=;{frac {1234}{10000},+,{frac {1234}{10000}{frac {1}{10000},+,{frac {1234}{10000}{frac}{frac {1}{10000}},+,{frac {1234}{10000}{frac} {frac}} {\fnMic} {1}{10000}},+,cdots }
donde coeficiente a = 1234/10000 y razón común r = 1/10000. La forma cerrada de la serie geométrica revela los dos números enteros que especifican el patrón repetido:
- 0.123412341234...... =a1− − r=1234/100001− − 1/10000=1234/100009999/10000=12349999.{displaystyle 0.123412341234ldots ;=;{frac {a}{1-r};=;{frac} {1234/10000}{1-1/10000};=;{frac {1234/10000}{9999/10000};=;{frac {1234}{9999}}
Serie de potencia
Al igual que la serie geométrica, la serie de potencias tiene un grado de libertad para su razón común r (a lo largo del eje x) pero tiene n+1 grados de libertad para sus coeficientes (a lo largo del eje y), donde n representa la potencia del último término de la serie parcial. En el mapa de polinomios, el gran círculo azul representa el conjunto de todas las series de potencias.
Serie Taylor
En matemáticas, la serie Taylor o Taylor expansión de una función es una suma infinita de términos que se expresan en términos de los derivados de la función en un solo punto. Para las funciones más comunes, la función y la suma de su serie Taylor son iguales cerca de este punto. Las series Taylor son nombradas por Brook Taylor, quien las presentó en 1715. Una serie Taylor también se llama una serie Maclaurin, cuando 0 es el punto en el que se consideran los derivados, después de Colin Maclaurin, que hizo uso amplio de este caso especial de la serie Taylor a mediados del siglo XVIII.
La suma parcial formada por la primera n + 1 términos de una serie Taylor es un polinomio de grado n que se llama nth Taylor polinomial of the function. Los polinomios de Taylor son aproximaciones de una función, que en general son mejores como n aumenta. El teorema de Taylor da estimaciones cuantitativas sobre el error introducido por el uso de tales aproximaciones. Si la serie Taylor de una función es convergente, su suma es el límite de la secuencia infinita de los polinomios Taylor. Una función puede diferir de la suma de su serie Taylor, incluso si su serie Taylor es convergente. Una función es analítica en un punto x si es igual a la suma de su Serie Taylor en un intervalo abierto (o disco abierto en el plano complejo) que contiene x. Esto implica que la función es analítica en cada punto del intervalo (o disco).Números codificados en binario
La serie geométrica de Zenón de Elea con coeficiente a=1/2 y razón común r=1/2 es la base de las aproximaciones de fracciones codificadas en binario en computadoras digitales. Concretamente, la serie geométrica escrita en su forma vectorial normalizada es s/a = [1 1 1 1 1 …][1 r r2 r3 r4 …]T. Manteniendo el vector columna de las funciones base [1 r r2 r3 r4 …]T lo mismo pero generalizando el vector fila [1 1 1 1 1 …] para que cada entrada pueda ser un 0 o un 1 permite una codificación aproximada de cualquier fracción. Por ejemplo, el valor v = 0,34375 se codifica como v/a = [0 1 0 1 1 0 …][1 r r2 r3 r4 …]T donde coeficiente a = 1/2 y razón común r = 1/2. Normalmente, el vector fila se escribe en la forma binaria más compacta v = 0,010110, que es 0,34375 en decimal.
Del mismo modo, la serie geométrica con coeficiente a=1 y razón común r=2 es la base para los enteros codificados en binario en las computadoras digitales. De nuevo, la serie geométrica escrita en su forma vectorial normalizada es s/a = [1 1 1 1 1 …][1 r r2 r3 r4 …]T. Manteniendo el vector columna de las funciones base [1 r r2 r3 r4 …]T lo mismo pero generalizando el vector fila [1 1 1 1 1 …] para que cada entrada pueda ser un 0 o un 1 permite una codificación de cualquier número entero. Por ejemplo, el valor v = 151 se codifica como v/a = [1 1 1 0 1 0 0 1 0 …][1 r r2 r3 r4 r5 r6 r7 r8 …]T donde el coeficiente a = 1 y la razón común r = 2. Por lo general, el vector fila se escribe en orden inverso (por lo que que el bit más significativo es el primero) en la forma binaria más compacta v = …010010111 = 10010111 que es 151 en decimal.
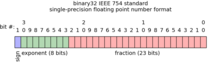
Como se muestra en la figura adyacente, la codificación binaria estándar de un número de coma flotante de 32 bits es una combinación de un entero codificado en binario y una fracción codificada en binario, comenzando en el bit más significativo con
- el bit de la señal, seguido por
- un campo de exponente entero de 8 bits con un supuesto offset de 127 (por lo que un valor de 127 representa un valor exponente de 0) y con una base de 2 significados que el valor exponente especifica un poco de cambio del campo de la fracción, seguido por
- un campo de fracción de 23 bits con un supuesto pero no codificado 1 sirviendo como el bit no cero más significativo de la fracción que estaría en posición 23 si fuera codificado.
Basándose en el ejemplo anterior de 0.34375 con codificación binaria de 0.010110, una codificación de punto flotante (según el estándar IEEE 754) de 0.34375 es
- el bit de señal que es 0 porque el número no es negativo,
- un campo de exponentes enteros de 8 bits que debe especificar un cambio que contrarresta el giro izquierdo de 2 bits para obtener la codificación binaria original de 0.010110 a 1.0110, y ese cambio contrario para recuperar la codificación binaria original es un cambio derecho de 2 bits que se especifica por un valor exponente de 125 (porque 125 − 127 = -2 que es un cambio derecho de 2 bits) que en binario es 0111 1101,
- un campo de fracción de 23 bits: 0,010 0000 0000 0000 000.
Aunque es posible codificar números de punto flotante a mano de esta manera, dejar que una computadora lo haga es más fácil y menos propenso a errores. El siguiente código de Julia confirma la codificación de punto flotante calculada a mano del número 0.34375:
julia> cadena de bits(Float32(0.34375))
"00111110101100000000000000000000"
Serie Laurent
Serie de Fourier compleja
Como ejemplo de la capacidad de la serie compleja de Fourier para trazar cualquier figura cerrada en 2D, en la animación adyacente, una serie compleja de Fourier traza la letra 'e' (para exponencial). Dada la intrincada coordinación de movimientos que se muestra en la animación, una definición de la compleja serie de Fourier puede ser sorprendentemente compacta en solo dos ecuaciones:
- s()t)=.. n=− − JUEGO JUEGO JUEGO JUEGO cne2π π intcn=∫ ∫ 01s()t)e− − 2π π intdt{displaystyle {begin{aligned}s(t) ventaja=sum _{n=-infty }{infty }c_{n}e^{2pi Intento ¿Qué?
donde la función parametrizada s(t) traza una figura cerrada 2D en el plano complejo a medida que el parámetro t avanza a través del período desde 0 a 1.
Para ayudar a dar sentido a estas ecuaciones compactas que definen la serie compleja de Fourier, tenga en cuenta que la suma de la serie compleja de Fourier se parece a la serie geométrica compleja excepto que la serie compleja de Fourier es básicamente dos series geométricas complejas (un conjunto de términos que giran en la dirección positiva y otro conjunto de términos que giran en la dirección negativa), y los coeficientes de la serie compleja de Fourier son constantes complejas que pueden variar de un término a otro. Al permitir que los términos giren en cualquier dirección, la serie se vuelve capaz de trazar cualquier figura cerrada en 2D. En cambio, la serie geométrica compleja tiene todos los términos girando en la misma dirección y solo puede trazar círculos. Permitir que los coeficientes de la serie geométrica compleja varíen de un término a otro ampliaría las formas que puede trazar, pero todas las formas posibles seguirían estando limitadas a ser hinchadas y parecidas a nubes, incapaces de trazar la forma de un segmento de línea simple., por ejemplo, yendo y viniendo entre 1 + i0 y -1 + i0. Sin embargo, la fórmula de Euler muestra que la suma de solo dos términos que giran en direcciones opuestas puede trazar ese segmento de línea entre 1 + i0 y -1 + i0:
- eiSilencio Silencio =# Silencio Silencio +ipecado Silencio Silencio e− − iSilencio Silencio =# Silencio Silencio − − ipecado Silencio Silencio # Silencio Silencio =eiSilencio Silencio +e− − iSilencio Silencio 2.{displaystyle {begin{aligned}e^{itheta ♪ ♪♪♪cos theta +isin theta \e^{-itheta ♪ ♪♪♪cos theta - isin theta \cos theta &={frac {e^{itheta }+e^{-itheta {fnMicrosoft Sans Serif}
En cuanto a la segunda ecuación compleja de la serie Fourier que define cómo calcular los coeficientes, el coeficiente del término no rotativo c0 se puede calcular integrando el complejo Serie Fourier primera ecuación en el rango de un período de 0 a 1. Sobre ese rango, todos los términos rotativos se integran a cero, dejando solo c0. Del mismo modo, cualquiera de los términos en la compleja serie Fourier primera ecuación se puede hacer para ser un término no rotativo multiplicando ambos lados de la ecuación por e− − 2π π int{displaystyle e^{-2pi int} antes de integrarse para calcular cn, y esa es la compleja serie Fourier segunda ecuación.
Matriz polinomio
En matemáticas, un polinomio matriz es un polinomio con matrices cuadradas como variables. Dado un polinomio normal y de valor escalar
- P()x)=.. i=0naixi=a0+a1x+a2x2+⋯ ⋯ +anxn,{displaystyle P(x)=sum ##{i=0} {n}{a_}x^{i}=a_{0}+a_{1}x+a_{2}x^{2}+cdots ¿Qué?
este polinomio evaluado en una matriz A es
- P()A)=.. i=0naiAi=a0I+a1A+a2A2+⋯ ⋯ +anAn,{displaystyle P(A)=sum ¿Por qué? ¿Qué?
Donde I es la matriz de identidad.
Una ecuación polinomial de matriz es una igualdad entre dos polinomios de matriz, que sostiene para las matrices específicas en cuestión. Una matriz de identidad polinomio es una ecuación polinomio matriz que sostiene para todos los matrices A en un anillo de matriz especificado Mn()R).Matriz exponencial
En matemáticas, la matriz exponencial es una función matriz en matrices cuadradas análogas a la función exponencial ordinaria. Se utiliza para resolver sistemas de ecuaciones diferenciales lineales. En la teoría de los grupos Lie, la matriz exponencial da el mapa exponencial entre una matriz Álgebra Lie y el correspondiente grupo Lie.
Vamos X ser un n×n matriz real o compleja. El exponencial de X, denotado por eX o exp(X), es el n×n matriz dada por la serie de potencia
Donde X0{displaystyle X^{0} se define como la matriz de identidad I{displaystyle Yo... con las mismas dimensiones X{displaystyle X}.
La serie anterior siempre converge, así que el exponencial de X está bien definido. Si X es una matriz 1×1 la matriz exponencial de X es una matriz 1×1 cuyo elemento único es el exponencial ordinario del elemento único X.Contenido relacionado
Desigualdad de Minkowski
Grupo solucionable
Problema de cumpleaños


























![{displaystyle G_{s}(n,r)=sum _{j=0}^{s}leftlbrace {s atop j}rightrbrace x^{j}{frac {d^{j}}{dx^{j}}}left[{frac {1-x^{n+1}}{1-x}}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf0345d5017a50622293433e999cc9a6f161b81c)













![{displaystyle sum _{k=0}^{infty }{frac {sin(kx)}{r^{k}}}={frac {1}{2i}}left[sum _{k=0}^{infty }left({frac {e^{ix}}{r}}right)^{k}-sum _{k=0}^{infty }left({frac {e^{-ix}}{r}}right)^{k}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25cf9f93893b1fd2d73c263c64a6850720217bca)


























![{displaystyle f(x)=arctan(u(x)){text{ is }}f'(x)=u'(x)/(1+[u(x)]^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eb96e30b5fb00c46b86214ae1895e618256d494)