Series de tiempo

En matemáticas, una serie temporal es una serie de puntos de datos indexados (o enumerados o graficados) en orden temporal. Más comúnmente, una serie de tiempo es una secuencia tomada en puntos sucesivos igualmente espaciados en el tiempo. Por tanto, es una secuencia de datos en tiempo discreto. Ejemplos de series temporales son las alturas de las mareas oceánicas, el recuento de manchas solares y el valor de cierre diario del Dow Jones Industrial Average.

Con mucha frecuencia, una serie temporal se traza mediante un gráfico de ejecución (que es un gráfico de líneas temporales). Las series de tiempo se utilizan en estadística, procesamiento de señales, reconocimiento de patrones, econometría, finanzas matemáticas, pronóstico del tiempo, predicción de terremotos, electroencefalografía, ingeniería de control, astronomía, ingeniería de comunicaciones y, en gran medida, en cualquier dominio de la ciencia e ingeniería aplicadas que implique mediciones temporales.

el análisis de series temporales comprende métodos para analizar datos de series temporales con el fin de extraer estadísticas significativas y otras características de los datos. La predicción de series temporales es el uso de un modelo para predecir valores futuros basándose en valores observados previamente. Si bien el análisis de regresión se emplea a menudo para probar las relaciones entre una o más series temporales diferentes, este tipo de análisis no suele denominarse "análisis de series temporales", que se refiere en particular a las relaciones entre diferentes puntos. en el tiempo dentro de una sola serie.

Los datos de series temporales tienen un orden temporal natural. Esto diferencia el análisis de series de tiempo de los estudios transversales, en los que no existe un orden natural de las observaciones (por ejemplo, explicar los salarios de las personas con referencia a sus respectivos niveles educativos, donde los datos de los individuos podrían ingresarse en cualquier orden). El análisis de series de tiempo también se diferencia del análisis de datos espaciales, donde las observaciones generalmente se relacionan con ubicaciones geográficas (por ejemplo, contabilizando los precios de las viviendas por ubicación, así como por las características intrínsecas de las casas). Un modelo estocástico para una serie temporal generalmente reflejará el hecho de que las observaciones cercanas en el tiempo estarán más estrechamente relacionadas que las observaciones más alejadas. Además, los modelos de series de tiempo a menudo harán uso del ordenamiento natural unidireccional del tiempo de modo que los valores de un período determinado se expresen como derivados de alguna manera de valores pasados, en lugar de valores futuros (ver reversibilidad temporal).

El análisis de series de tiempo se puede aplicar a datos continuos de valor real, datos numéricos discretos o datos simbólicos discretos (es decir, secuencias de caracteres, como letras y palabras en el idioma inglés).

Métodos de análisis

Los métodos para el análisis de series de tiempo se pueden dividir en dos clases: métodos en el dominio de la frecuencia y métodos en el dominio del tiempo. Los primeros incluyen análisis espectral y análisis de wavelets; estos últimos incluyen análisis de autocorrelación y correlación cruzada. En el dominio del tiempo, la correlación y el análisis se pueden realizar en forma de filtro utilizando correlación escalada, mitigando así la necesidad de operar en el dominio de la frecuencia.

Además, las técnicas de análisis de series de tiempo se pueden dividir en métodos paramétricos y no paramétricos. Los enfoques paramétricos suponen que el proceso estocástico estacionario subyacente tiene una determinada estructura que puede describirse utilizando un pequeño número de parámetros (por ejemplo, utilizando un modelo autorregresivo o de media móvil). En estos enfoques, la tarea es estimar los parámetros del modelo que describe el proceso estocástico. Por el contrario, los enfoques no paramétricos estiman explícitamente la covarianza o el espectro del proceso sin suponer que el proceso tenga una estructura particular.

Los métodos de análisis de series temporales también se pueden dividir en lineales y no lineales, univariados y multivariados.

Datos del panel

Una serie temporal es un tipo de datos de panel. Los datos de panel son la clase general, un conjunto de datos multidimensional, mientras que un conjunto de datos de series temporales es un panel unidimensional (al igual que un conjunto de datos transversal). Un conjunto de datos puede presentar características tanto de datos de panel como de datos de series temporales. Una forma de saberlo es preguntar qué hace que un registro de datos sea único respecto de los demás registros. Si la respuesta es el campo de datos de tiempo, entonces este es un candidato a conjunto de datos de series de tiempo. Si para determinar un registro único se requiere un campo de datos de tiempo y un identificador adicional que no está relacionado con el tiempo (por ejemplo, identificación de estudiante, símbolo bursátil, código de país), entonces es candidato a datos de panel. Si la diferenciación se basa en el identificador no temporal, entonces el conjunto de datos es un candidato a conjunto de datos transversal.

Análisis

Hay varios tipos de motivación y análisis de datos disponibles para series temporales que son apropiados para diferentes propósitos.

Motivación

En el contexto de la estadística, la econometría, las finanzas cuantitativas, la sismología, la meteorología y la geofísica, el objetivo principal del análisis de series de tiempo es la previsión. En el ámbito del procesamiento de señales, la ingeniería de control y la ingeniería de comunicaciones se utiliza para la detección de señales. Otras aplicaciones son la minería de datos, el reconocimiento de patrones y el aprendizaje automático, donde el análisis de series de tiempo se puede utilizar para agrupación, clasificación, consulta por contenido, detección de anomalías y pronósticos.

Análisis exploratorio

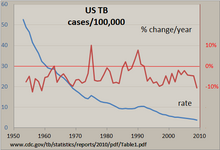
Una forma sencilla de examinar una serie temporal regular es manualmente con un gráfico de líneas. A la derecha se muestra un gráfico de ejemplo de la incidencia de tuberculosis en los Estados Unidos, elaborado con un programa de hoja de cálculo. El número de casos se estandarizó a una tasa por 100.000 y se calculó el cambio porcentual anual en esta tasa. La línea que cae casi de manera constante muestra que la incidencia de la tuberculosis estaba disminuyendo en la mayoría de los años, pero el cambio porcentual en esta tasa varió hasta +/- 10%, con "aumentos repentinos" en la mayoría de los años. en 1975 y alrededor de principios de los años 1990. El uso de ambos ejes verticales permite comparar dos series temporales en un solo gráfico.

Un estudio de analistas de datos corporativos encontró dos desafíos para el análisis exploratorio de series temporales: descubrir la forma de patrones interesantes y encontrar una explicación para estos patrones. Las herramientas visuales que representan datos de series temporales como matrices de mapas de calor pueden ayudar a superar estos desafíos.

Otras técnicas incluyen:

• Análisis de autocorrelación para examinar la dependencia serial
• Análisis espectral para examinar el comportamiento cíclico que no necesita estar relacionado con la estacionalidad. Por ejemplo, la actividad de manchas solares varía más de 11 ciclos anuales. Otros ejemplos comunes incluyen fenómenos celestes, patrones meteorológicos, actividad neuronal, precios de los productos básicos y actividad económica.
• Separación en componentes que representan tendencia, estacionalidad, variación lenta y rápida, e irregularidad cíclica: ver estimación de tendencias y descomposición de series temporales

Ajuste de curva

El ajuste de curvas es el proceso de construir una curva, o función matemática, que se ajuste mejor a una serie de puntos de datos, posiblemente sujeta a restricciones. El ajuste de curvas puede implicar interpolación, donde se requiere un ajuste exacto de los datos, o suavizado, en el que se obtiene un ajuste "suave" Se construye una función que se ajusta aproximadamente a los datos. Un tema relacionado es el análisis de regresión, que se centra más en cuestiones de inferencia estadística, como cuánta incertidumbre está presente en una curva que se ajusta a los datos observados con errores aleatorios. Las curvas ajustadas se pueden utilizar como ayuda para la visualización de datos, para inferir valores de una función cuando no hay datos disponibles y para resumir las relaciones entre dos o más variables. La extrapolación se refiere al uso de una curva ajustada más allá del rango de los datos observados y está sujeta a un grado de incertidumbre ya que puede reflejar el método utilizado para construir la curva tanto como refleja los datos observados.

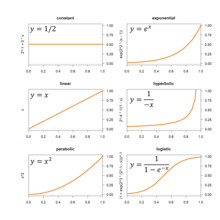
Para los procesos que generalmente se espera que crezcan en magnitud, una de las curvas en el gráfico de la derecha (y muchas otras) se puede ajustar estimando sus parámetros.

La construcción de series de tiempo económicas implica la estimación de algunos componentes para algunas fechas mediante interpolación entre valores ("benchmarks") para fechas anteriores y posteriores. La interpolación es la estimación de una cantidad desconocida entre dos cantidades conocidas (datos históricos), o sacar conclusiones sobre información faltante a partir de la información disponible ("lectura entre líneas"). La interpolación es útil cuando los datos que rodean a los datos faltantes están disponibles y se conocen su tendencia, estacionalidad y ciclos a más largo plazo. Esto se suele hacer utilizando una serie relacionada conocida para todas las fechas relevantes. Alternativamente, se utiliza la interpolación polinómica o la interpolación spline donde las funciones polinómicas por partes se ajustan en intervalos de tiempo de manera que encajen suavemente entre sí. Un problema diferente que está estrechamente relacionado con la interpolación es la aproximación de una función complicada mediante una función simple (también llamada regresión). La principal diferencia entre regresión e interpolación es que la regresión polinómica proporciona un polinomio único que modela todo el conjunto de datos. Sin embargo, la interpolación spline produce una función continua por partes compuesta de muchos polinomios para modelar el conjunto de datos.

La extrapolación es el proceso de estimar, más allá del rango de observación original, el valor de una variable en función de su relación con otra variable. Es similar a la interpolación, que produce estimaciones entre observaciones conocidas, pero la extrapolación está sujeta a una mayor incertidumbre y a un mayor riesgo de producir resultados sin sentido.

Aproximación de funciones

En general, un problema de aproximación de funciones nos pide que seleccionemos una función entre una clase bien definida que coincida estrechamente ("se aproxima") a una función objetivo de una manera específica de la tarea. Se pueden distinguir dos clases principales de problemas de aproximación de funciones: primero, para funciones objetivo conocidas, la teoría de la aproximación es la rama del análisis numérico que investiga cómo ciertas funciones conocidas (por ejemplo, funciones especiales) pueden ser aproximadas por una clase específica de funciones (por ejemplo, ejemplo, polinomios o funciones racionales) que a menudo tienen propiedades deseables (cálculos económicos, continuidad, valores integrales y límite, etc.).

En segundo lugar, la función objetivo, llámela g, puede ser desconocida; en lugar de una fórmula explícita, solo se proporciona un conjunto de puntos (una serie de tiempo) de la forma (x, g(x)). Dependiendo de la estructura del dominio y codominio de g, pueden ser aplicables varias técnicas para aproximar g. Por ejemplo, si g es una operación con números reales, se pueden utilizar técnicas de interpolación, extrapolación, análisis de regresión y ajuste de curvas. Si el codominio (rango o conjunto objetivo) de g es un conjunto finito, se trata de un problema de clasificación. Un problema relacionado con la aproximación de series temporales en línea es resumir los datos en una sola pasada y construir una representación aproximada que pueda admitir una variedad de consultas de series temporales con límites en el peor de los casos.

Hasta cierto punto, los diferentes problemas (regresión, clasificación, aproximación de aptitud) han recibido un tratamiento unificado en la teoría estadística del aprendizaje, donde se consideran problemas de aprendizaje supervisado.

Predicción y previsión

En estadística, la predicción es parte de la inferencia estadística. Un enfoque particular de dicha inferencia se conoce como inferencia predictiva, pero la predicción se puede realizar dentro de cualquiera de los diversos enfoques de la inferencia estadística. De hecho, una descripción de la estadística es que proporciona un medio para transferir conocimientos sobre una muestra de una población a toda la población y a otras poblaciones relacionadas, lo que no es necesariamente lo mismo que una predicción en el tiempo. Cuando la información se transfiere a lo largo del tiempo, a menudo a momentos específicos, el proceso se conoce como pronóstico.

• Modelos estadísticos totalmente formados para fines de simulación estocástica, a fin de generar versiones alternativas de la serie de tiempo, representando lo que podría suceder en períodos de tiempo no específicos en el futuro
• Modelos estadísticos simples o totalmente formados para describir el posible resultado de la serie de tiempo en el futuro inmediato, dado conocimiento de los resultados más recientes (previsión).
• El pronóstico de la serie de tiempo se hace generalmente utilizando paquetes de software estadístico automatizados y lenguajes de programación, como Julia, Python, R, SAS, SPSS y muchos otros.
• El pronóstico de datos a gran escala se puede hacer con Apache Spark usando la biblioteca Spark-TS, un paquete de terceros.

Clasificación

Asignar un patrón de serie temporal a una categoría específica, por ejemplo, identificar una palabra basándose en una serie de movimientos de la mano en lenguaje de señas.

Estimación de señal

Este enfoque se basa en el análisis armónico y el filtrado de señales en el dominio de la frecuencia utilizando la transformada de Fourier y la estimación de la densidad espectral, cuyo desarrollo fue acelerado significativamente durante la Segunda Guerra Mundial por el matemático Norbert Wiener y los ingenieros eléctricos Rudolf E. Kálmán., Dennis Gabor y otros para filtrar señales del ruido y predecir valores de señales en un momento determinado. Consulte Filtro de Kalman, Teoría de estimación y Procesamiento de señales digitales.

Segmentación

Dividir una serie temporal en una secuencia de segmentos. A menudo ocurre que una serie temporal puede representarse como una secuencia de segmentos individuales, cada uno con sus propias propiedades características. Por ejemplo, la señal de audio de una conferencia telefónica se puede dividir en partes correspondientes a los momentos en que cada persona estuvo hablando. En la segmentación de series de tiempo, el objetivo es identificar los puntos límite del segmento en la serie de tiempo y caracterizar las propiedades dinámicas asociadas con cada segmento. Se puede abordar este problema utilizando la detección de puntos de cambio o modelando la serie temporal como un sistema más sofisticado, como un sistema lineal de salto de Markov.

Modelos

Los modelos para datos de series temporales pueden tener muchas formas y representar diferentes procesos estocásticos. Al modelar variaciones en el nivel de un proceso, tres grandes clases de importancia práctica son los modelos autorregresivos (AR), los modelos integrados (I) y los . modelos de media móvil (MA). Estas tres clases dependen linealmente de puntos de datos anteriores. Las combinaciones de estas ideas producen modelos de media móvil autorregresiva (ARMA) y de media móvil autorregresiva integrada (ARIMA). El modelo autorregresivo de media móvil fraccionariamente integrada (ARFIMA) generaliza los tres primeros. Las extensiones de estas clases para tratar datos con valores vectoriales están disponibles bajo el título de modelos multivariados de series de tiempo y, a veces, los acrónimos anteriores se amplían incluyendo una inicial "V" para "vector", como en VAR para vector autorregresión. Un conjunto adicional de extensiones de estos modelos está disponible para su uso cuando la serie temporal observada es impulsada por algún tipo de "forzamiento" series de tiempo (que pueden no tener un efecto causal en la serie observada): la diferencia con el caso multivariado es que la serie forzada puede ser determinista o estar bajo el control del experimentador. Para estos modelos, las siglas se amplían con una "X" para "exógeno".

La dependencia no lineal del nivel de una serie con respecto a puntos de datos anteriores es de interés, en parte debido a la posibilidad de producir una serie temporal caótica. Sin embargo, lo que es más importante, las investigaciones empíricas pueden indicar la ventaja de utilizar predicciones derivadas de modelos no lineales, sobre aquellas de modelos lineales, como por ejemplo en los modelos exógenos autorregresivos no lineales. Otras referencias sobre análisis de series de tiempo no lineales: (Kantz y Schreiber) y (Abarbanel)

Entre otros tipos de modelos de series temporales no lineales, existen modelos para representar los cambios de varianza a lo largo del tiempo (heterocedasticidad). Estos modelos representan heterocedasticidad condicional autorregresiva (ARCH) y la colección comprende una amplia variedad de representaciones (GARCH, TARCH, EGARCH, FIGARCH, CGARCH, etc.). Aquí los cambios en la variabilidad están relacionados con, o predichos por, valores pasados recientes de la serie observada. Esto contrasta con otras posibles representaciones de variabilidad que varía localmente, donde la variabilidad podría modelarse como impulsada por un proceso separado que varía en el tiempo, como en un modelo doblemente estocástico.

En trabajos recientes sobre análisis sin modelos, los métodos basados en transformadas wavelet (por ejemplo, wavelets localmente estacionarias y redes neuronales descompuestas en wavelets) han ganado popularidad. Las técnicas multiescala (a menudo denominadas multiresolución) descomponen una serie de tiempo determinada, intentando ilustrar la dependencia del tiempo en múltiples escalas. Véase también las técnicas de conmutación multifractal de Markov (MSMF) para modelar la evolución de la volatilidad.

Un modelo oculto de Markov (HMM) es un modelo estadístico de Markov en el que se supone que el sistema que se está modelando es un proceso de Markov con estados no observados (ocultos). Un HMM puede considerarse como la red bayesiana dinámica más simple. Los modelos HMM se utilizan ampliamente en el reconocimiento de voz, para traducir una serie temporal de palabras habladas en texto.

Notación

Se utilizan varias notaciones diferentes para el análisis de series temporales. Se escribe una notación común que especifica una serie de tiempo X indexada por números naturales.

X =X₁, X₂,...).

Otra notación común es

Y =Y_t: t ▪ T),

donde T es el conjunto de índices.

Condiciones

Hay dos conjuntos de condiciones bajo las cuales se construye gran parte de la teoría:

• Proceso estacionario
• Proceso ergonódico

La ergodicidad implica estacionariedad, pero lo contrario no es necesariamente el caso. La estacionariedad generalmente se clasifica en estacionariedad estricta y estacionariedad de sentido amplio o de segundo orden. Tanto los modelos como las aplicaciones pueden desarrollarse bajo cada una de estas condiciones, aunque los modelos en el último caso podrían considerarse sólo parcialmente especificados.

Además, el análisis de series de tiempo se puede aplicar cuando las series son estacionalmente estacionarias o no estacionarias. Las situaciones en las que las amplitudes de los componentes de frecuencia cambian con el tiempo se pueden abordar en el análisis tiempo-frecuencia que utiliza una representación tiempo-frecuencia de una serie temporal o señal.

Herramientas

Las herramientas para investigar datos de series temporales incluyen:

• Consideración de la función de autocorrelación y de la función de densidad espectral (también funciones de intercorrelación y funciones de densidad transversal)
• Funciones transversales y autocorrelación escaladas para eliminar las contribuciones de componentes lentos
• Realizar una transformación Fourier para investigar la serie en el dominio de frecuencia
• Divulgación, espectro continuo o mezclado de series temporales, dependiendo de si la serie de tiempo contiene una señal armónica (generalizada) o no
• Uso de un filtro para eliminar ruido no deseado
• Análisis de componentes principales (o análisis de funciones ortogonales empíricas)
• Análisis del espectro singular
• Modelos estructurales:
  • General State Space Models
  • Modelos de componentes no merecidos
• Machine Learning
  • Redes neuronales artificiales
  • Soporte de máquina vectorial
  • Fuzzy logic
  • Proceso gaisiano
  • Programación genética
  • Programación de expresión genética
  • Modelo Oculto Markov
  • Programación de múltiples expresiones
• Análisis de la teoría de búsqueda
• Gráfico de control
  • Gráfico de control individual Shewhart
  • Gráfico CUSUM
  • Gráfico EWMA
• Análisis de la fluctuación
• Modelo de efectos mixtos no lineales
• Tiempo dinámico en espera
• Dynamic Bayesian network
• Técnicas de análisis de frecuencias temporales:
  • Transformación rápida Fourier
  • Transformación de onda continua
  • Transformación de Fourier a corto plazo
  • Chirplet transform
  • Transformación de Fourier
• Análisis caótico
  • Dimensión de correlación
  • Parcelas de repetición
  • Análisis de la cuantificación de la repetición
  • Los exponentes de Lyapunov
  • Entropy encoding

Medidas

Métricas o funciones de series temporales que se pueden utilizar para la clasificación de series temporales o el análisis de regresión:

• Medidas lineales unilaterales
  • Momento (matemática)
  • Potencia de banda espectral
  • Frecuencia del borde espectral
  • Energía acumulada (proceso de firmas)
  • Características de la función de autocorrelación
  • Parámetros de honor
  • Parámetros FFT
  • Parámetros del modelo autoregresivo
  • Prueba Mann-Kendall
• Medidas no lineales univariadas
  • Medidas basadas en la suma de correlación
  • Dimensión de correlación
  • Correlación integral
  • Densidad de correlación
  • Correlación entropía
  • Entropía aproximada
  • Muestra entropía
  • Fourier entropyuk
  • Wavelet entropy
  • Dispersión entropía
  • Entropía de dispersión de fluctuación
  • Rényi entropy
  • Métodos de orden superior
  • Previsibilidad marginal
  • Índice de similitud dinámica
  • Medidas de disimilaridad del espacio estatal
  • Lyapunov exponent
  • Métodos de permutación
  • Corriente local
• Otras medidas univarias
  • Complejidad algorítmica
  • Estimaciones de complejidad de Kolmogorov
  • Hidden Markov Estados modelo
  • Rough path signature
  • Recorrido de series temporales y corrección de surroga
  • Pérdida de recurrencia (grado de no estacionalidad)
• Medidas lineales bivariadas
  • Máximo cruce lineal
  • Coherencia lineal (procesamiento de firmas)
• Medidas bivariadas no lineales
  • interdependencia no lineal
  • Formación dinámica (física)
  • Medidas adoptadas Sincronización de fase
  • Medidas Locking de fase
• Medidas de similitud:
  • Cruz-correlación
  • Tiempo dinámico Warping
  • Modelos de Markov ocultos
  • Editar distancia
  • Correlación total
  • Estimador de Newey-West
  • Prais – Transformación biológica
  • Datos como vectores en un espacio metrizable
    • Distancia Minkowski
    • Distancia Mahalanobis
  • Datos como serie de tiempo con sobres
    • Global standard deviation
    • Local standard deviation
    • Desviación estándar con ventana
  • Datos interpretados como series estocásticas
    • Coeficiente de correlación de productos de Pearson
    • Coeficiente de correlación de rango de Spearman
  • Datos interpretados como función de distribución de probabilidad
    • Prueba de Kolmogorov–Smirnov
    • Cramér-von Mises criterion

Visualización

Las series de tiempo se pueden visualizar con dos categorías de gráficos: gráficos superpuestos y gráficos separados. Los gráficos superpuestos muestran series de todos los tiempos en el mismo diseño, mientras que los gráficos separados las presentan en diferentes diseños (pero alineados para fines de comparación).

Gráficos superpuestos

• Gráficos trenzados
• Gráficos de línea
• Gráficos de pendiente
• GapChartfr

Gráficos separados

• Gráficos horizontales
• Tabla de línea reducida (pequeñas múltiples)
• Gráfico de Silhouette
• Gráfico de silueta circular