Serie convergente

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Serie matemática con una suma finita

En matemáticas, una serie es la suma de los términos de una secuencia infinita de números. Más precisamente, una secuencia infinita ${displaystyle (a_{1},a_{2},a_{3},ldots)}$ define una serie $S$ que se denota

{displaystyle S=a_{1}+a_{2}+a_{3}+cdots =sum _{k=1}^{infty }a_{k}.}

La $n$ ésima suma parcial $S n$ es la suma de los primeros $n$ términos de la secuencia; eso es,

{displaystyle S_{n}=a_{1}+a_{2}+cdots +a_{n}=sum _{k=1}^{n}a_{k}.}

Una serie es convergente (o convergencias) si y sólo si la secuencia ${displaystyle (S_{1},S_{2},S_{3},dots)}$ de sus sumas parciales tiende a un límite; eso significa que, al añadir una ${displaystyle a_{k}}$ después de la otra en el orden dado por los índices, uno obtiene sumas parciales que se acercan y se acercan a un número determinado. Más precisamente, una serie converge, si y sólo si existe un número ${displaystyle ell }$ tal que por cada número arbitrariomente pequeño positivo ${displaystyle varepsilon }$ , hay un (suficientemente grande) entero ${displaystyle N}$ tal que para todos ${displaystyle ngeq N}$ ,

<math alttext="{displaystyle left|S_{n}-ell right|SilencioSn− − l l Silencioc)ε ε .{displaystyle left habitS_{n}-ell right respondiendo correctamente buscadovarepsilon.}<img alt="{displaystyle left|S_{n}-ell right|

Si la serie es convergente, el número (necesariamente único) ${displaystyle ell }$ se llama suma de la serie.

La misma notación

{displaystyle sum _{k=1}^{infty }a_{k}}

se utiliza para la serie y, si es convergente, para su suma. Esta convención es similar a la que se utiliza para la suma: $a + b$ denota la operación de sumar $a$ y $b$ así como el resultado de esta suma, que se denomina suma de $a$ y $b$ .

Cualquier serie que no sea convergente se dice que es divergente o divergente.

Ejemplos de series convergentes y divergentes

Los recíprocos de los enteros positivos producen una serie divergente (serie tormónica):
${displaystyle {1 over 1}+{1 over 2}+{1 over 3}+{1 over 4}+{1 over 5}+{1 over 6}+cdots rightarrow infty.}$
Alternar los signos de los reciprocos de los enteros positivos produce una serie convergente (serie armónica alternante):
${displaystyle {1 over 1}-{1 over 2}+{1 over 3}-{1 over 4}+{1 over 5}-cdots =ln(2)}$
Los reciprocales de números primos producen una serie divergente (por lo que el conjunto de primos es "grande"; ver divergencia de la suma de los reciprocales de los primos):
${displaystyle {1 over 2}+{1 over 3}+{1 over 5}+{1 over 7}+{1 over 11}+{1 over 13}+cdots rightarrow infty.}$
Los recíprocos de los números triangulares producen una serie convergente:
${displaystyle {1 over 1}+{1 over 3}+{1 over 6}+{1 over 10}+{1 over 15}+{1 over 21}+cdots =2.}$
Los recíprocos de los factores producen una serie convergente (véase e):
${displaystyle {frac {1}{1}}+{frac {1}{1}}+{frac {1}{2}}+{frac {1}{6}}+{frac {1}{24}}+{frac {1}{120}}+cdots =e.}$
Los recíprocos de números cuadrados producen una serie convergente (el problema de Basilea):
${displaystyle {1 over 1}+{1 over 4}+{1 over 9}+{1 over 16}+{1 over 25}+{1 over 36}+cdots ={pi ^{2} over 6}.}$
Los poderes recíprocos de 2 producen una serie convergente (por lo que el conjunto de poderes de 2 es "pequeño"):
${displaystyle {1 over 1}+{1 over 2}+{1 over 4}+{1 over 8}+{1 over 16}+{1 over 32}+cdots =2.}$
Los recíprocos de poderes de cualquier n título1 producen una serie convergente:
${displaystyle {1 over 1}+{1 over n}+{1 over n^{2}}+{1 over n^{3}}+{1 over n^{4}}+{1 over n^{5}}+cdots ={n over n-1}.}$
Alternar los signos de reciprocos de poderes de 2 también produce una serie convergente:
${displaystyle {1 over 1}-{1 over 2}+{1 over 4}-{1 over 8}+{1 over 16}-{1 over 32}+cdots ={2 over 3}.}$
Alternating the signs of reciprocals of powers of any n título1 produces a convergent series:
${displaystyle {1 over 1}-{1 over n}+{1 over n^{2}}-{1 over n^{3}}+{1 over n^{4}}-{1 over n^{5}}+cdots ={n over n+1}.}$
Los recíprocos de los números Fibonacci producen una serie convergente (ver ):
${displaystyle {frac {1}{1}}+{frac {1}{1}}+{frac {1}{2}}+{frac {1}{3}}+{frac {1}{5}}+{frac {1}{8}}+cdots =psi.}$

Pruebas de convergencia

Existen varios métodos para determinar si una serie converge o diverge.

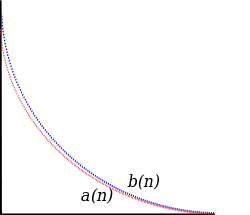
Prueba de comparación. Los términos de la secuencia ${displaystyle left{a_{n}right}}$ se comparan con los de otra secuencia ${displaystyle left{b_{n}right}}$ . Si, para todos n, ${displaystyle 0leq a_{n}leq b_{n}}$ , y ${textstyle sum _{n=1}^{infty }b_{n}}$ converge, entonces lo hace ${textstyle sum _{n=1}^{infty }a_{n}.}$

Sin embargo, si, para todos n, ${displaystyle 0leq b_{n}leq a_{n}}$ , y ${textstyle sum _{n=1}^{infty }b_{n}}$ divergencias, entonces lo hace ${textstyle sum _{n=1}^{infty }a_{n}.}$

Prueba de proporción. Supongamos que para todos n, ${displaystyle a_{n}}$ no es cero. Supongamos que existe ${displaystyle r}$ tales que

{displaystyle lim _{nto infty }left|{frac {a_{n+1}}{a_{n}}}right|=r.}

Si r < 1, entonces la serie es absolutamente convergente. Si r > 1, entonces la serie diverge. Si r = 1, la prueba de razón no es concluyente y la serie puede converger o divergir.

Prueba de raíz o nprueba de raíz. Supongamos que los términos de la secuencia en cuestión no son negativos. Defina r de la siguiente manera:

{displaystyle r=limsup _{nto infty }{sqrt[{n}]{|a_{n}|}},}

donde "lim sup" denota el límite superior (posiblemente ∞; si el límite existe es el mismo valor).

Si r < 1, entonces la serie converge. Si r > 1, entonces la serie diverge. Si r = 1, la prueba de la raíz no es concluyente y la serie puede converger o divergir.

La prueba de razón y la prueba de raíz se basan en la comparación con una serie geométrica y, como tales, funcionan en situaciones similares. De hecho, si la prueba de razón funciona (lo que significa que el límite existe y no es igual a 1), entonces también funciona la prueba de raíz; lo contrario, sin embargo, no es cierto. Por lo tanto, la prueba de la raíz es aplicable de manera más general, pero como cuestión práctica, el límite suele ser difícil de calcular para tipos de series que se ven comúnmente.

Prueba integral. La serie puede compararse con una integral para establecer convergencia o divergencia. Vamos. ${displaystyle f(n)=a_{n}}$ ser una función positiva y monotonicamente decreciente. Si

<math alttext="{displaystyle int _{1}^{infty }f(x),dx=lim _{tto infty }int _{1}^{t}f(x),dx∫ ∫ 1JUEGO JUEGO f()x)dx=limt→ → JUEGO JUEGO ∫ ∫ 1tf()x)dxc)JUEGO JUEGO ,{displaystyle int _{1}{infty }f(x),dx=lim _{tto infty }int _{1}}{t}f(x),dx se hizo infty}<img alt="{displaystyle int _{1}^{infty }f(x),dx=lim _{tto infty }int _{1}^{t}f(x),dx

entonces la serie converge. Pero si la integral diverge, entonces la serie también lo hace.

Prueba de comparación de límites. Si $0}" xmlns="http://www.w3.org/1998/Math/MathML">{}an},{}bn}■0{displaystyle ¿Qué?0}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/60f524fb94bd5400fed577bd71a499f8441dff62" style="vertical-align: -0.838ex; width:14.996ex; height:2.843ex;"/>$ , y el límite ${displaystyle lim _{nto infty }{frac {a_{n}}{b_{n}}}}$ existe y no es cero, entonces ${textstyle sum _{n=1}^{infty }a_{n}}$ converge si y sólo si ${textstyle sum _{n=1}^{infty }b_{n}}$ converge.

Prueba de serie alternada. También conocido como criterio de Leibniz, la prueba de serie alterna indica que para una serie alternada de la forma ${textstyle sum _{n=1}^{infty }a_{n}(-1)^{n}}$ , si ${displaystyle left{a_{n}right}}$ está disminuyendo monótonamente, y tiene un límite de 0 en el infinito, entonces la serie converge.

Prueba de condensación de Cauchy. Si ${displaystyle left{a_{n}right}}$ es una secuencia decreciente de monotona positiva, entonces ${textstyle sum _{n=1}^{infty }a_{n}}$ converge si y sólo si ${textstyle sum _{k=1}^{infty }2^{k}a_{2^{k}}}$ converge.

Prueba de Dirichlet

La prueba de Abel

Convergencia condicional y absoluta

Para cualquier secuencia ${displaystyle left{a_{1}, a_{2}, a_{3},dots right}}$ , ${displaystyle a_{n}leq left|a_{n}right|}$ para todos n. Por lo tanto,

{displaystyle sum _{n=1}^{infty }a_{n}leq sum _{n=1}^{infty }left|a_{n}right|.}

Esto significa que si ${textstyle sum _{n=1}^{infty }left|a_{n}right|}$ converge, entonces ${textstyle sum _{n=1}^{infty }a_{n}}$ también converge (pero no viceversa).

Si la serie ${textstyle sum _{n=1}^{infty }left|a_{n}right|}$ converge, entonces la serie ${textstyle sum _{n=1}^{infty }a_{n}}$ es absolutamente convergente. La serie Maclaurin de la función exponencial es absolutamente convergente para cada valor complejo de la variable.

Si la serie ${textstyle sum _{n=1}^{infty }a_{n}}$ converge pero la serie ${textstyle sum _{n=1}^{infty }left|a_{n}right|}$ divergencias, entonces la serie ${textstyle sum _{n=1}^{infty }a_{n}}$ es condicionalmente convergente. La serie Maclaurin de la función Logarithm ${displaystyle ln(1+x)}$ es condicionalmente convergente para $x = 1$ .

El teorema de la serie de Riemann establece que si una serie converge condicionalmente, es posible reordenar los términos de la serie de tal manera que la serie converja a cualquier valor, o incluso diverja.

Convergencia uniforme

Vamos. ${displaystyle left{f_{1}, f_{2}, f_{3},dots right}}$ ser una secuencia de funciones. La serie ${textstyle sum _{n=1}^{infty }f_{n}}$ se dice que convergen uniformemente a fsi la secuencia ${displaystyle {s_{n}}}$ de sumas parciales definidas por

{displaystyle s_{n}(x)=sum _{k=1}^{n}f_{k}(x)}

convege uniformemente a f.

Existe un análogo de la prueba de comparación para series infinitas de funciones llamada prueba M de Weierstrass.

Criterio de convergencia de Cauchy

El criterio de convergencia de Cauchy establece que una serie

{displaystyle sum _{n=1}^{infty }a_{n}}

converge si y sólo si la secuencia de sumas parciales es una secuencia Cauchy. Esto significa que para todos $0,}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0,{displaystyle varepsilon >0,}0,}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4d780d8dff4b26013c7d5d0efbc1acb92b60645b" style="vertical-align: -0.671ex; width:5.991ex; height:2.509ex;"/>$ hay un entero positivo ${displaystyle N}$ tal que para todos ${displaystyle ngeq mgeq N}$ tenemos

<math alttext="{displaystyle left|sum _{k=m}^{n}a_{k}right|Silencio. . k=mnakSilencioc)ε ε .{displaystyle left durablesum Bien escrito.<img alt="{displaystyle left|sum _{k=m}^{n}a_{k}right|

Esto equivale a

$m}left|sum _{k=m}^{n}a_{k}right|right)=0.}" xmlns="http://www.w3.org/1998/Math/MathML">limm→ → JUEGO JUEGO ()Supn■mSilencio. . k=mnakSilencio)=0.{displaystyle lim _{mto infty }left(sup _{n confidencialm}left durablesum ¿Por qué?m}left|sum _{k=m}^{n}a_{k}right|right)=0.}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c97ea9b029029777a0349f296d309d6c96e7606b" style="vertical-align: -3.171ex; width:25.377ex; height:7.509ex;"/>$

Más resultados...