Segundo momento polar del área

El segundo momento polar de la zona, también conocido (corrientemente, coloquialmente) como "momento de inercia" o incluso "momento de inercia", es una cantidad utilizada para describir la resistencia a la deformación torsional (deflexión), en objetos (o segmentos de un objeto) con una sección transversal invariante y sin disyunciones significativas o deformación externa. Es un componente del segundo momento de área, vinculado a través del teorema de eje perpendicular. Donde planar segundo momento de área describe la resistencia de un objeto a la deflexión (bender) cuando se somete a una fuerza aplicada a un plano paralelo al eje central, el polar segundo momento de área describe la resistencia de un objeto a la deflexión cuando se somete a un momento aplicado en un plano perpendicular al eje central del objeto (es decir, paralelo a la sección transversal). Similar a planar segundo momento de cálculos de área (${\displaystyle I_{x}$,${\displaystyle I_{y}$, y ${\displaystyle I_{xy}$), el polar segundo momento de área a menudo se denota como ${\displaystyle I_{z}$. Mientras que varios libros de texto de ingeniería y publicaciones académicas también lo denotan como ${\displaystyle J}$ o ${\displaystyle J_{z}$, esta designación debe ser dada cuidadosa atención para que no se confunda con la torsión constante, ${\displaystyle J_{t}$, utilizado para objetos no cilíndricos.

En términos simples, el momento polar de área es la resistencia de un eje o viga a ser distorsionado por torsión, en función de su forma. La rigidez proviene únicamente del área de la sección transversal del objeto y no depende de su composición material o módulo de corte. Cuanto mayor sea la magnitud del segundo momento polar de área, mayor será la rigidez torsional del objeto.

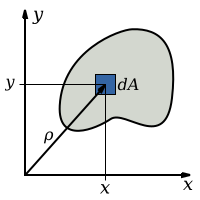
La ecuación que describe el momento polar del área es una integral múltiple sobre el área transversal, ${\displaystyle A}$, del objeto.

$${\displaystyle J=\iint ¿Qué?$$Donde ${\displaystyle r}$ es la distancia al elemento ${\displaystyle dA}$.

Sustituyendo a ${\displaystyle x}$ y ${\displaystyle y}$ componentes, utilizando el teorema pitagórico: $${\displaystyle J=\iint _{A}\left(x^{2}+y^{2}\right)dx\,dy}$$$${\displaystyle J= ¿Por qué? - Sí.$$

Dada la planar segundo momento de ecuaciones de área, donde: $${\displaystyle I_{x}=\iint - Sí.$$$${\displaystyle I_{y}=\iint ¿Qué?$$

Se muestra que el momento polar de la zona se puede describir como la suma de la ${\displaystyle x}$ y ${\displaystyle y}$ planar momentos de área, ${\displaystyle I_{x}$ y ${\displaystyle I_{y}$$${\displaystyle\therefore J=I_{z}=I_{x}+I_{y}$$

Esto también se muestra en el teorema del eje perpendicular. Para objetos que tengan simetría rotacional, como un cilindro o tubo hueco, la ecuación se puede simplificar para: $${\displaystyle J=2I_{x}$$ o $${\displaystyle J=2I_{y}$$

Para una sección circular con radio ${\displaystyle R.$: $${\displaystyle I_{z}= ################################################################################################################################################################################################################################################################ ¿Por qué? ¿Qué?$$

La unidad del SI para el segundo momento de área polar, al igual que el segundo momento de área planar, es el metro a la cuarta potencia (m⁴), y la pulgada a la cuarta potencia (in⁴) en unidades tradicionales de EE. UU. y unidades imperiales.

El segundo momento polar de la zona puede ser insuficiente para analizar las vigas y los ejes con secciones transversales no circulares, debido a su tendencia a la urdimbre cuando se torna, causando deformaciones fuera de plano. En tales casos, debe sustituirse una constante de torsión, cuando se incluya una constante de deformación adecuada para compensar el efecto de calentamiento. Dentro de esto, hay artículos que diferencian entre segundo momento polar de la zona, ${\displaystyle I_{z}$, y torsional constante, ${\displaystyle J_{t}$, ya no uso ${\displaystyle J}$ para describir el segundo momento polar de la zona.

En el caso de objetos con una variación significativa de la sección transversal (a lo largo del eje del par aplicado), que no se pueden analizar en segmentos, puede ser necesario utilizar un enfoque más complejo. Véase elasticidad 3D.

Aunque el segundo momento polar de la zona se utiliza con más frecuencia para calcular el desplazamiento angular de un objeto sometido a un momento (torque) aplicado paralelamente a la sección transversal, el valor proporcionado de la rigidez no tiene ningún impacto en la resistencia torsional proporcionada a un objeto como una función de sus materiales constitutivos. La rigidez proporcionada por el material de un objeto es una característica de su módulo de corte, ${\displaystyle G.$. Combinando estas dos características con la longitud del eje, ${\displaystyle L.$, se puede calcular la deflexión angular de un eje, ${\displaystyle \theta }$, debido al par aplicado, ${\displaystyle T}$: $${\displaystyle \theta ={\frac {TL}{JG}}$$

Como se muestra, cuanto mayor sea el módulo de corte y el momento polar del área del material (es decir, mayor área de la sección transversal), mayor será la resistencia a la deflexión torsional.

El segundo momento polar del área aparece en las fórmulas que describen la tensión torsional y el desplazamiento angular.

Presiones torsionales: $${\displaystyle \tau ={\frac {T\,R}{J_{z}}}$$Donde ${\displaystyle \tau }$ es el estrés torsional, ${\displaystyle T}$ es el par aplicado, ${\displaystyle r}$ es la distancia del eje central, y ${\displaystyle J_{z}$ es el segundo momento polar de la zona.

Nota: En un eje circular, la tensión cortante es máxima en la superficie del eje.

Cálculo del radio del eje de una turbina de vapor para un turbogrupo:

Suposiciones:

• La potencia transportada por el eje es 1000 MW; esto es típico para una gran central nuclear.
• Rendimiento del estrés del acero utilizado para hacer el eje (τ_rendimiento) es: 250 × 10⁶ N/m².
• Electricidad tiene una frecuencia de 50 Hz; esta es la frecuencia típica de Europa. En América del Norte la frecuencia es 60 Hz. Esto supone que hay una correlación 1:1 entre la velocidad rotacional de la turbina y la frecuencia de la potencia de las barras.

La frecuencia angular se puede calcular con la siguiente fórmula: $${\displaystyle \omega =2\pi f}$$

El par que lleva el eje está relacionado con el poder por la siguiente ecuación: $${\displaystyle P=T\omega }$$

Por lo tanto, la frecuencia angular es 314,16 rad/s y el par 3,1831 × 10⁶ N·m.

El par máximo es: $${\displaystyle T_{\max }={\frac {\tau _{\max - Sí.$$

Después de la sustitución de la segundo momento polar de la zona se obtiene la siguiente expresión: $${\displaystyle r={\sqrt[{3}{\frac {2T_{\max }{\pi \tau _{\max }$$

El radio es r=0,200 m = 200 mm, o un diámetro de 400 mm. Si se añade un factor de seguridad de 5 y se vuelve a calcular el radio con la tensión admisible igual a τ_adm=τ_{límite elástico}/5, el resultado es un radio de 0,343 m, o un diámetro de 690 mm, el tamaño aproximado del eje de un turboconjunto en una central nuclear.

Segundo momento de la zona polar: $${\displaystyle I_{z}={\frac {\pi\left(D^{4}-d^{4}\right)}{32}}$$

Momento de inercia: $${\displaystyle I_{c}=I_{z}\rho l={\frac {\pi\rho l\left(D^{4}-d^{4}\right)}{64}}$$

Segundo momento polar del área $${\displaystyle I_{z}={\frac {\pi} ¿Qué?$$

Momento de inercia $${\displaystyle I_{c}=I_{z}\rho l={\frac {\pi\rho ID^{4} {64}}$$Donde:

• ${\displaystyle d}$ es el diámetro interior en metros (m)
• ${\displaystyle D}$ es el diámetro exterior en metros (m)
• ${\displaystyle I_{c}$ es el momento de la inercia en kg· m²
• ${\displaystyle I_{z}$ es el segundo momento polar de la zona en metros a la cuarta potencia (m⁴)
• ${\displaystyle l}$ es la longitud de los cilindros en metros (m)
• ${\displaystyle \rho }$ es la masa específica en kg/m³

• Torsión constante
• Torsion spring
• Suspensión de la barra de torsión
• Segundo momento de área
• Modulo de la manguera
• Lista de segundos momentos de área

• Torsion of Shafts - engineeringtoolbox.com
• Propiedades elásticas y Young Modulus para algunos materiales - engineeringtoolbox.com
• Base de datos de propiedades materiales - matweb.com