Segunda ley de la termodinámica

La segunda ley de la termodinámica es una ley física basada en la experiencia universal sobre las interconversiones de calor y energía. Una declaración simple de la ley es que el calor siempre se mueve de los objetos más calientes a los objetos más fríos (o 'cuesta abajo'), a menos que se suministre energía de alguna forma para invertir la dirección del flujo de calor. Otra definición es: "No toda la energía térmica se puede convertir en trabajo en un proceso cíclico."

La segunda ley de la termodinámica en otras versiones establece el concepto de entropía como una propiedad física de un sistema termodinámico. Se puede utilizar para predecir si los procesos están prohibidos a pesar de obedecer el requisito de conservación de la energía expresado en la primera ley de la termodinámica y proporciona los criterios necesarios para los procesos espontáneos. La segunda ley puede formularse mediante la observación de que la entropía de los sistemas aislados que se dejan a la evolución espontánea no puede disminuir, ya que siempre llegan a un estado de equilibrio termodinámico donde la entropía es máxima a la energía interna dada. Un aumento en la entropía combinada del sistema y el entorno explica la irreversibilidad de los procesos naturales, a los que a menudo se hace referencia en el concepto de la flecha del tiempo.

Históricamente, la segunda ley fue un hallazgo empírico que se aceptó como un axioma de la teoría termodinámica. La mecánica estadística proporciona una explicación microscópica de la ley en términos de distribuciones de probabilidad de los estados de grandes conjuntos de átomos o moléculas. La segunda ley se ha expresado de muchas maneras. Su primera formulación, que precedió a la propia definición de entropía y se basó en la teoría calórica, es el teorema de Carnot, formulado por el científico francés Sadi Carnot, quien en 1824 demostró que la eficiencia de conversión de calor en trabajo en un calor motor tiene un límite superior. La primera definición rigurosa de la segunda ley basada en el concepto de entropía provino del científico alemán Rudolf Clausius en la década de 1850 e incluía su declaración de que el calor nunca puede pasar de un cuerpo más frío a uno más caliente sin que ocurra algún otro cambio, relacionado con él, en el Mismo tiempo.

La segunda ley de la termodinámica permite definir el concepto de temperatura termodinámica, apoyándose también en la ley cero de la termodinámica.

Introducción

Calor que fluye del agua caliente al agua fría

La primera ley de la termodinámica proporciona la definición de la energía interna de un sistema termodinámico, y expresa su cambio para un sistema cerrado en términos de trabajo y calor. Puede estar vinculada a la ley de conservación de la energía. La segunda ley se ocupa de la dirección de los procesos naturales. Afirma que un proceso natural funciona sólo en un sentido, y no es reversible. Por ejemplo, cuando se pone a disposición un camino de conducción o radiación, el calor siempre fluye espontáneamente de un cuerpo más caliente a un cuerpo más frío. Estos fenómenos se contabilizan en términos de cambio de entropía. Si un sistema aislado que contiene subsistemas distintos se mantiene inicialmente en equilibrio termodinámico interno partiendo internamente por paredes impermeables entre los subsistemas, y luego alguna operación hace que las paredes sean más permeables, entonces el sistema evoluciona espontáneamente para alcanzar un nuevo equilibrio termodinámico interno final, y su entropía total, ${displaystyle S.$, aumenta.

En un proceso reversible o cuasi estático idealizado de transferencia de energía como calor a un sistema termodinámico cerrado de interés, (que permite la entrada o salida de energía – pero no transferencia de materia), de un sistema termodinámico auxiliar, un incremento infinitesimal (${displaystyle mathrm {d} S}$) en la entropía del sistema de interés se define como resultado de una transferencia infinitesimal de calor (${displaystyle delta Q}$) al sistema de interés, dividido por la temperatura termodinámica común ${displaystyle (T)}$ del sistema de interés y el sistema termodinámico auxiliar:

${displaystyle mathrm {d} S={frac {delta ¿Qué?$

Se utilizan diferentes notaciones para una cantidad infinita de calor ${displaystyle (delta)}$ y cambio infinitesimal de entropía ${displaystyle (mathrm {d})}$ porque la entropía es una función de estado, mientras que el calor, como el trabajo, no lo es.

Para un proceso infinitesimal realmente posible sin intercambio de masa con el entorno, la segunda ley requiere que el incremento en la entropía del sistema cumpla la desigualdad

${displaystyle mathrm {d} Sió {frac {delta ¿Qué?$

Esto se debe a que un proceso general para este caso (sin intercambio de masa entre el sistema y su entorno) puede incluir trabajo realizado sobre el sistema por su entorno, que puede tener efectos de fricción o viscosos dentro del sistema, porque una reacción química puede estar en progreso, o porque la transferencia de calor solo ocurre de manera irreversible, impulsada por una diferencia finita entre la temperatura del sistema (T) y la temperatura del entorno (T_surr).

Tenga en cuenta que la igualdad aún se aplica para el flujo de calor puro (solo flujo de calor, sin cambios en la composición química y la masa),

${displaystyle mathrm {d} S={frac {delta ¿Qué?$

que es la base de la determinación precisa de la entropía absoluta de sustancias puras a partir de las curvas de capacidad calorífica medidas y los cambios de entropía en las transiciones de fase, es decir, por calorimetría.

Introducción de un conjunto de variables internas ${displaystyle xi }$ para describir la desviación de un sistema termodinámico de un estado de equilibrio químico en equilibrio físico (con la presión uniforme bien definida necesaria P y temperatura T), uno puede registrar la igualdad

${displaystyle mathrm {d} S={frac} {delta ¿Qué? {1}{T}sum _{j},Xi _{j},delta xi ¿Por qué?$

El segundo término representa el trabajo de las variables internas que pueden ser perturbadas por influencias externas, pero el sistema no puede realizar ningún trabajo positivo a través de las variables internas. Esta declaración introduce la imposibilidad de la reversión de la evolución del sistema termodinámico en el tiempo y puede considerarse como una formulación del segundo principio de la termodinámica: la formulación, que es, por supuesto, equivalente a la formulación del principio en términos de entropía.

La ley cero de la termodinámica en su breve enunciado habitual permite reconocer que dos cuerpos en una relación de equilibrio térmico tienen la misma temperatura, especialmente que un cuerpo de prueba tiene la misma temperatura que un cuerpo termométrico de referencia. Para un cuerpo en equilibrio térmico con otro, existen indefinidamente muchas escalas empíricas de temperatura, en general dependiendo respectivamente de las propiedades de un cuerpo termométrico de referencia particular. La segunda ley permite una escala de temperatura distinguida, que define una temperatura termodinámica absoluta, independiente de las propiedades de cualquier cuerpo termométrico de referencia en particular.

Diversas declaraciones de la ley

La segunda ley de la termodinámica se puede expresar de muchas maneras específicas, siendo las declaraciones clásicas más destacadas la declaración de Rudolf Clausius (1854), la declaración de Lord Kelvin (1851) y la declaración en termodinámica axiomática de Constantin Carathéodory (1909). Estas declaraciones expresan la ley en términos físicos generales citando la imposibilidad de ciertos procesos. Se ha demostrado que las declaraciones de Clausius y Kelvin son equivalentes.

Principio de Carnot

El origen histórico de la segunda ley de la termodinámica está en el análisis teórico del flujo de calor en las máquinas de vapor de Sadi Carnot (1824). La pieza central de ese análisis, ahora conocida como máquina de Carnot, es una máquina térmica ideal operada ficticiamente en el modo límite de lentitud extrema conocido como cuasi-estático, de modo que las transferencias de calor y trabajo se dan entre subsistemas que siempre están en su propio interior. Estados de equilibrio termodinámico. Representa la eficiencia máxima teórica de un motor térmico que opera entre dos depósitos térmicos o térmicos dados a diferentes temperaturas. El principio de Carnot fue reconocido por Carnot en un momento en que la teoría calórica representaba la comprensión dominante de la naturaleza del calor, antes del reconocimiento de la primera ley de la termodinámica y antes de la expresión matemática del concepto de entropía. Interpretado a la luz de la primera ley, el análisis de Carnot es físicamente equivalente a la segunda ley de la termodinámica y sigue siendo válido en la actualidad. Algunas muestras de su libro son:

...donde exista una diferencia de temperatura, se puede producir energía motriz.

La producción de energía móvil se debe entonces en motores de vapor no a un consumo real de calorías, pero a su transporte de un cuerpo caliente a un cuerpo frío...

El poder móvil del calor es independiente de los agentes empleados para realizarlo; su cantidad se fija únicamente por las temperaturas de los cuerpos entre los cuales se efectúa, finalmente, la transferencia de calorías.

En términos modernos, el principio de Carnot puede expresarse con mayor precisión:

La eficiencia de un ciclo de Carnot cuasi estático o reversible depende sólo de las temperaturas de los dos depósitos de calor, y es el mismo, sea cual sea la sustancia de trabajo. Un motor Carnot operado de esta manera es el motor de calor más eficiente posible utilizando esas dos temperaturas.

Declaración de Clausius

El científico alemán Rudolf Clausius sentó las bases de la segunda ley de la termodinámica en 1850 al examinar la relación entre la transferencia de calor y el trabajo. Su formulación de la segunda ley, que se publicó en alemán en 1854, se conoce como la declaración de Clausius:

El calor nunca puede pasar de un cuerpo más frío a un cuerpo más cálido sin algún otro cambio, conectado con él, que ocurre al mismo tiempo.

La declaración de Clausius utiliza el concepto de 'paso de calor'. Como es habitual en los debates sobre termodinámica, esto significa "transferencia neta de energía en forma de calor" y no se refiere a las transferencias contributivas en un sentido u otro.

El calor no puede fluir espontáneamente de regiones frías a regiones calientes sin que se realice un trabajo externo en el sistema, lo cual es evidente a partir de la experiencia ordinaria de refrigeración, por ejemplo. En un refrigerador, el calor se transfiere de frío a caliente, pero solo cuando es forzado por un agente externo, el sistema de refrigeración.

Declaraciones de Kelvin

Lord Kelvin expresó la segunda ley en varios términos.

Es imposible que una máquina de autoactuación, sin la ayuda de ninguna agencia externa, transmita el calor de un cuerpo a otro a una temperatura superior.

Es imposible, por medio de la agencia material inanimada, derivar efecto mecánico de cualquier parte de la materia enfriándola por debajo de la temperatura del más frío de los objetos circundantes.

Equivalencia de las declaraciones de Clausius y Kelvin

Declaración de Kelvin derivada de Clausius

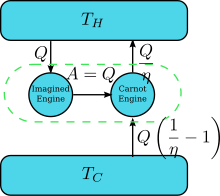
Supongamos que hay un motor que viola la declaración de Kelvin: es decir, uno que drena el calor y lo convierte completamente en trabajo (el calor drenado se convierte totalmente en trabajo) de una manera cíclica sin ningún otro resultado. Ahora emparejarlo con un motor Carnot inverso como se muestra por la figura correcta. La eficiencia de un motor de calor normal es . por lo que la eficiencia del motor de calor inverso es 1/.. El efecto neto y único del par combinado de motores es transferir calor ${textstyle Delta Q=Qleft({frac {1}{eta }-1right)}$ desde el embalse más fresco hasta el más caliente, que viola la declaración de Clausius. Esta es una consecuencia de la primera ley de la termodinámica, en cuanto a la energía total del sistema para seguir siendo la misma; ${textstyle {text{Input}}+{text{Output}=0implies (Q+Q_{c})-{frac {Q}{eta }=0}$, por lo tanto ${textstyle Q_{c}=Qleft({frac {1}{eta }-1right)}$, donde (1) se utiliza la convención de señal de calor en la que el calor entra (saliendo de) un motor es positivo (negativo) y (2) ${displaystyle {frac}{eta} }$ se obtiene por la definición de eficiencia del motor cuando la operación del motor no se invierte. Así, una violación de la declaración de Kelvin implica una violación de la declaración de Clausius, es decir, la declaración de Clausius implica la declaración de Kelvin. Podemos demostrar de manera similar que la declaración de Kelvin implica la declaración de Clausius, y por lo tanto los dos son equivalentes.

La propuesta de Planck

Planck ofreció la siguiente proposición como derivada directamente de la experiencia. Esto a veces se considera como su declaración de la segunda ley, pero lo consideró como un punto de partida para la derivación de la segunda ley.

Es imposible construir un motor que funcionará en un ciclo completo, y no producirá ningún efecto excepto la elevación de un peso y el enfriamiento de un depósito de calor.

Relación entre el enunciado de Kelvin y la proposición de Planck

Es casi habitual en los libros de texto hablar de la "declaración de Kelvin-Planck" de la ley, como por ejemplo en el texto de ter Haar y Wergeland. Esta versión, también conocida como el enunciado del motor térmico, de la segunda ley establece que

Es imposible diseñar un dispositivo cíclicamente operativo, cuyo único efecto es absorber energía en forma de calor desde un único reservorio térmico y entregar una cantidad equivalente de trabajo.

Declaración de Planck

Planck estableció la segunda ley de la siguiente manera.

Cada proceso que ocurre en la naturaleza procede en el sentido en que se aumenta la suma de las entropías de todos los cuerpos que participan en el proceso. En el límite, es decir, para procesos reversibles, la suma de las entropías sigue sin cambiar.

Algo parecido a la afirmación de Planck es la de Uhlenbeck y Ford para los fenómenos irreversibles.

... en un cambio irreversible o espontáneo de un estado de equilibrio a otro (como por ejemplo la igualdad de temperatura de dos cuerpos A y B, cuando se pone en contacto) la entropía siempre aumenta.

Principio de Carathéodory

Constantin Carathéodory formuló la termodinámica sobre una base axiomática puramente matemática. Su declaración de la segunda ley se conoce como el Principio de Carathéodory, que puede formularse de la siguiente manera:

En cada barrio de cualquier estado S de un sistema cerrado adiabaticamente hay estados inaccesibles de S.

Con esta formulación, describió por primera vez el concepto de accesibilidad adiabática y proporcionó la base para un nuevo subcampo de termodinámica clásica, a menudo llamada termodinámica geométrica. Se deriva del principio de Carathéodory de que la cantidad de energía transferida cuasi estáticamente como calor es una función de proceso holonomic, en otras palabras, ${displaystyle delta Q=TdS}$.

Aunque es casi habitual en los libros de texto decir que el principio de Carathéodory expresa la segunda ley y tratarlo como equivalente a los enunciados de Clausius o de Kelvin-Planck, ese no es el caso. Para obtener todo el contenido de la segunda ley, el principio de Carathéodory debe complementarse con el principio de Planck, que el trabajo isocórico siempre aumenta la energía interna de un sistema cerrado que inicialmente estaba en su propio equilibrio termodinámico interno.

Principio de Planck

En 1926, Max Planck escribió un importante artículo sobre los fundamentos de la termodinámica. Indicó el principio

La energía interna de un sistema cerrado se incrementa por un proceso adiabático, durante el cual el volumen del sistema permanece constante.

Esta formulación no menciona el calor y no menciona la temperatura, ni siquiera la entropía, y no necesariamente se basa implícitamente en esos conceptos, pero implica el contenido de la segunda ley. Una declaración estrechamente relacionada es que "La presión de fricción nunca hace un trabajo positivo". Planck escribió: "La producción de calor por fricción es irreversible".

Sin mencionar la entropía, este principio de Planck se expresa en términos físicos. Está muy relacionado con la declaración de Kelvin dada justo arriba. Es relevante que para un sistema a volumen y número de moles constantes, la entropía es una función monótona de la energía interna. Sin embargo, este principio de Planck no es en realidad el enunciado preferido de Planck de la segunda ley, que se cita anteriormente, en una subsección anterior de la presente sección de este artículo, y se basa en el concepto de entropía.

Borgnakke y Sonntag hacen una declaración que, en cierto sentido, es complementaria al principio de Planck. No lo ofrecen como una declaración completa de la segunda ley:

... sólo hay una manera en la que se puede disminuir la entropía de un sistema [cerrado], y eso es transferir el calor del sistema.

A diferencia del principio anterior de Planck, este se aplica explícitamente en términos de cambio de entropía. La eliminación de materia de un sistema también puede disminuir su entropía.

Enunciado para un sistema que tiene una expresión conocida de su energía interna en función de sus variables de estado extensivas

Se ha demostrado que la segunda ley es equivalente a que la energía interna U sea una función débilmente convexa, cuando se escribe en función de propiedades extensivas (masa, volumen, entropía,...).

Corolarios

Movimiento perpetuo de segunda especie

Antes del establecimiento de la segunda ley, muchas personas que estaban interesadas en inventar una máquina de movimiento perpetuo habían tratado de eludir las restricciones de la primera ley de la termodinámica extrayendo la energía interna masiva del entorno como potencia de la máquina. Tal máquina se llama "máquina de movimiento perpetuo del segundo tipo". La segunda ley declaraba la imposibilidad de tales máquinas.

Teorema de Carnot

El teorema de Carnot (1824) es un principio que limita la eficiencia máxima para cualquier motor posible. La eficiencia depende únicamente de la diferencia de temperatura entre los depósitos térmicos fríos y calientes. El teorema de Carnot establece:

• Todos los motores de calor irreversibles entre dos depósitos de calor son menos eficientes que un motor Carnot operando entre los mismos depósitos.
• Todos los motores de calor reversibles entre dos depósitos de calor son igualmente eficientes con un motor Carnot operando entre los mismos depósitos.

En su modelo ideal, el calor del calórico convertido en trabajo podría restablecerse invirtiendo el movimiento del ciclo, un concepto conocido posteriormente como reversibilidad termodinámica. Carnot, sin embargo, postuló además que algo de caloría se pierde y no se convierte en trabajo mecánico. Por lo tanto, ninguna máquina térmica real podía darse cuenta de la reversibilidad del ciclo de Carnot y estaba condenada a ser menos eficiente.

Aunque se formuló en términos de calórico (ver la teoría calórica obsoleta), en lugar de entropía, esta fue una primera visión de la segunda ley.

Desigualdad de Clausius

El teorema de Clausius (1854) establece que en un proceso cíclico

${displaystyle oint {frac {delta ¿Qué? 0.}$

La igualdad se cumple en el caso reversible y la desigualdad estricta se cumple en el caso irreversible, con T_surr como la temperatura del baño de calor (alrededor) aquí. El caso reversible se utiliza para introducir la función de estado entropía. Esto se debe a que en los procesos cíclicos la variación de una función de estado es cero a partir de la funcionalidad de estado.

Temperatura termodinámica

Para un motor térmico arbitrario, la eficiencia es:

${displaystyle eta ={frac {fnh} {fnh} {fnh} {fnh}} {fnh}}} {fnfn}}} {fn}}}}}} {fnfnfnfnfn}}} {fnf}}}}fnfnfnfnfnh}}}}}}}}}}}}}}\\\\fnfnfnfnfnfnfn\fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnh}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnh}}}}}}fn {q_{H}+q_{C} {q_{H}=1-{frac} {fnK} {fnK}} {fnK}}}} {fn}}}}} {cH}}}} {fn}}}}}}}}}}}} {cH}}}}$

()1)

donde W_n es el trabajo neto realizado por el motor por ciclo, q_H > 0 es el calor agregado al motor desde un depósito caliente, y q_C = - |q_C| < 0 es el calor residual emitido a un depósito frío desde el motor. Así, la eficiencia depende únicamente de la relación |q_C| / |q_H|.

El teorema de Carnot establece que todos los motores reversibles que operan entre los mismos depósitos de calor son igualmente eficientes. Así, cualquier máquina térmica reversible que funcione entre las temperaturas T_H y T_C debe tener la misma eficiencia, es decir decir, la eficiencia es una función de las temperaturas solamente:

${fnMicroc} Oh, Dios mío.$

()2)

Además, una máquina térmica reversible que funcione entre las temperaturas T₁ y T₃ debe tener la misma eficiencia como aquella que consta de dos ciclos, uno entre T₁ y otro (intermedio) de temperatura T₂, y el segundo entre T₂ y T₃, donde T₁ > T₂ > T₃. Esto se debe a que, si una parte del motor de dos tiempos está oculta de tal manera que se reconoce como un motor entre los depósitos a las temperaturas T₁ y T₃, entonces la eficiencia de este motor debe ser la misma que la del otro motor en los mismos depósitos. Si elegimos motores tales que el trabajo realizado por el motor de un ciclo y el motor de dos ciclos sea el mismo, entonces la eficiencia de cada motor térmico se escribe como se muestra a continuación.

${displaystyle eta ##{1}=1-{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}=1-f(T_{1},T_{3}}}$,

${displaystyle eta ##{2}=1-{frac {fnK_} {cH00}}}=1-f(T_{1},T_{2}}}}$,

${displaystyle eta ##{3}=1-{frac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}=1-f(T_{2},T_{3}}}$.

Aquí, el motor 1 es el motor de un ciclo, y los motores 2 y 3 hacen el motor de dos ciclos donde hay el depósito intermedio en T₂. También hemos utilizado el hecho de que el calor ${displaystyle q_{2}$ pasa por el depósito térmico intermedio en ${displaystyle T_{2}$ sin perder su energía. (I.e., ${displaystyle q_{2}$ no se pierde durante su paso por el embalse en ${displaystyle T_{2}$.) Este hecho puede ser probado por lo siguiente.

${displaystyle {begin{aligned} }_{2}=1-{frac {fnK} {fnK} {fnh}}to}t} - ¿Qué? }_{3}=1-{frac {fnK} {fnK} {f}} {fnK}} {f}}} {to}}} {to}}} {to}}}} {f}}}} {to}}}}} {to}} {to}} {to}}}}} {to}}}}}}}} {to}}}} {to}}}}}}} {to}}}}}}}}}}}}}}}} {to}}}}}}}}}}} {to}}}}}}}}}}} {to}}}}}}}}}}}}}}}}} {to {to}}}}} {to}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {to}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {} {}} {}} {}}} {}}} {}} {}}} {}} {}}} {}} {}} {}} {}} {}}} {}} {}}}} {} {}} {}}}}} {}}}}}} {}}}}}}}}}} {}}}}}}} {}}}}}}}}} {}}}}}}} {}}}}}}} {}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}} }_{1}=1-{frac {fnK} {fnK} {fnK} {f}}}h}h} {fnK}} {f}} {f}} {f}} {f}}} {fn}}} {f}}}} {f}}} {f}}}}}} {f}}}}}}}}}\\\f}}}}}}}}}}}}\\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\\\\\\\fn}}}}}}}\\\\\\\\\fn}}}}}}}}}}}}}}}}}}\\\\\\\fn}}}}}}}}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {} {}} {}} {}} {}} {} {}} {} {}} {}} {}} {} {}} {}}} {}} {}}} {}} {}}}} {} {}} {}}}}} {}}}}}} {}}}}}}} {}}}}}} {}}}}}}}} {}}}}}}} {}}}}} {}}} {}} {}}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}} {}}}} {}}}}}}}} {}}}}}} {} {}}}} {}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}$

Para tener la consistencia en la última ecuación, el calor ${displaystyle q_{2}$ fluido del motor 2 al depósito intermedio debe ser igual al calor ${displaystyle q_{2}{*}$ fluido desde el embalse hasta el motor 3.

Entonces

${displaystyle f(T_{1},T_{3})={frac {fnK} {fnMicroc}} {fnK}}} {fnK}}} {fnK}} {f}}}}} {fnK}}}}}}} {fnfn}}}}} {fnfnf}} Oh, Dios mío.$

Ahora considere el caso donde ${displaystyle T_{1}$ es una temperatura de referencia fija: la temperatura del triple punto de agua como 273.16 Kelvin; ${displaystyle T_{1}=273.16K}$. Entonces para cualquier T₂ y T₃,

${displaystyle f(T_{2},T_{3})={frac {f(T_{1},T_{3}}{f(T_{1},T_{2}}={frac {273.16{text{ K}cdot}cdot} f(T_{1},T_{3}}{273.16{text{ K}cdot f(T_{1}}}}$

Por lo tanto, si la temperatura termodinámica T* está definida por

${displaystyle T^{*}=273.16{text{ K}cdot f(T_{1},T)}$

entonces la función f, vista como una función de las temperaturas termodinámicas, es simplemente

${displaystyle f(T_{2},T_{3})=f(T_{2}^{*},T_{3}^{*})={frac} {fnMicrosoft Sans Serif}$

y la temperatura de referencia T₁* = 273,16 K × f(T_{1< /sub>,T1) = 273,16 K. (Se puede usar cualquier temperatura de referencia y cualquier valor numérico positivo; la elección aquí corresponde a la escala Kelvin).}

Entropía

Según la igualdad de Clausius, para un proceso reversible

${displaystyle oint {frac {delta Q} {T}=0}$

Eso significa la línea integral ${displaystyle int _{L}{frac {delta Q} {T}}$ es un camino independiente para procesos reversibles.

Entonces podemos definir una función de estado S llamada entropía, que para un proceso reversible o para una transferencia de calor pura satisface

${displaystyle dS={frac {delta Q} {T}}$

Con esto solo podemos obtener la diferencia de entropía integrando la fórmula anterior. Para obtener el valor absoluto, necesitamos la tercera ley de la termodinámica, que establece que S = 0 en el cero absoluto para cristales perfectos.

Para cualquier proceso irreversible, dado que la entropía es una función de estado, siempre podemos conectar los estados inicial y terminal con un proceso reversible imaginario e integrar en ese camino para calcular la diferencia de entropía.

Ahora invierta el proceso reversible y combínelo con dicho proceso irreversible. Aplicando la desigualdad de Clausius en este ciclo, con T_surr como la temperatura del entorno,

${displaystyle Delta S+int {frac {delta ¿Qué? ¿Qué? 0}$

Por lo tanto,

${displaystyle Delta Sgeq int {frac {delta ¿Qué?$

donde la igualdad se cumple si la transformación es reversible.

Observe que si el proceso es un proceso adiabático, entonces ${displaystyle delta Q=0}$Así que ${displaystyle Delta Sgeq 0}$.

Energía, trabajo útil disponible

Un caso especial idealizado importante y revelador es considerar la aplicación de la segunda ley al escenario de un sistema aislado (llamado sistema total o universo), compuesto por dos partes: un subsistema de interés y el subsistema entorno del sistema. Se imagina que estos alrededores son tan grandes que pueden considerarse como un depósito de calor ilimitado a temperatura T_R y presión P< sub>R – de modo que no importa cuánto calor se transfiera hacia (o desde) el subsistema, la temperatura del entorno permanecerá T_R ; y no importa cuánto se expanda (o contraiga) el volumen del subsistema, la presión del entorno seguirá siendo P_R.

Cualesquiera que sean los cambios en dS y dS_R que ocurran en las entropías del subsistema y los alrededores individualmente, la entropía S_tot del sistema total aislado no debe disminuir según la segunda ley de la termodinámica:

${displaystyle dS_{mathrm {tot} }=dS+dS_{R}geq 0}$

Según la primera ley de la termodinámica, el cambio dU en la energía interna del subsistema es la suma del calor δq agregado al subsistema, menos cualquier trabajo δw realizado por el subsistema, más cualquier energía química neta que ingrese al subsistema d Σμ_iRN_i, de modo que:

${displaystyle dU=delta q-delta w+dleft(sum mu ¿Por qué?$

donde μ_iR son los potenciales químicos de las especies químicas en el entorno externo.

Ahora el calor que sale del depósito y entra al subsistema es

${displaystyle delta q=T_{R}(-dS_{R})leq T_{R}dS}$

donde usamos por primera vez la definición de entropía en la termodinámica clásica (alternativamente, en la termodinámica estadística, se puede derivar la relación entre el cambio de entropía, la temperatura y el calor absorbido); y luego la desigualdad de la Segunda Ley desde arriba.

Por lo tanto, cualquier trabajo neto δw realizado por el subsistema debe obedecer

${displaystyle delta wleq -dU+T_{R}dS+sum mu ¿Qué?$

Es útil separar el trabajo δw realizado por el subsistema en el trabajo útil δw_u que puede ser realizado por el subsistema, más allá del trabajo p_R dV realizado simplemente por el subsistema que se expande contra el entorno externo presión, dando la siguiente relación para el trabajo útil (exergía) que se puede realizar:

${displaystyle delta w_{u}leq -dleft(U-T_{R}S+p_{R}V-sum mu _{iR}N_{i}right)}$

Es conveniente definir el lado derecho como la derivada exacta de un potencial termodinámico, llamado disponibilidad o exergía E del subsistema,

${displaystyle E=U-T_{R}S+p_{R}V-sum mu _{iR}N_{i}}$

Por lo tanto, la Segunda Ley implica que para cualquier proceso que pueda considerarse dividido simplemente en un subsistema y un depósito ilimitado de temperatura y presión con el que está en contacto,

${displaystyle dE+delta w_{u}leq 0}$

es decir el cambio en la exergía del subsistema más el trabajo útil realizado por el subsistema (o, el cambio en la exergía del subsistema menos cualquier trabajo, adicional al realizado por el depósito de presión, hecho en el sistema) debe ser menor o igual a cero.

En resumen, si se elige un estado de referencia adecuado similar a un depósito infinito como entorno del sistema en el mundo real, entonces la segunda ley predice una disminución en E para un proceso irreversible y ningún cambio para un proceso reversible.

${displaystyle DS_{tot}geq 0}$ equivale a ${displaystyle dE+delta w_{u}leq 0}$

Esta expresión, junto con el estado de referencia asociado, permite que un ingeniero de diseño que trabaje en la escala macroscópica (por encima del límite termodinámico) utilice la segunda ley sin medir o considerar directamente el cambio de entropía en un sistema aislado total. (Además, ver ingeniero de procesos). Esos cambios ya han sido considerados por la suposición de que el sistema bajo consideración puede alcanzar el equilibrio con el estado de referencia sin alterar el estado de referencia. También se puede encontrar una eficiencia para un proceso o conjunto de procesos que lo compare con el ideal reversible (Ver eficiencia de la segunda ley).

Este enfoque de la segunda ley se utiliza ampliamente en la práctica de la ingeniería, la contabilidad ambiental, la ecología de sistemas y otras disciplinas.

Dirección de procesos espontáneos

La segunda ley determina si un proceso físico o químico propuesto está prohibido o puede ocurrir espontáneamente. Para sistemas aislados, el entorno no proporciona energía y la segunda ley requiere que la entropía del sistema solo debe aumentar: ΔS > 0. Ejemplos de procesos físicos espontáneos en sistemas aislados incluyen los siguientes:

• 1) El calor se puede transferir de una región de temperatura superior a una temperatura inferior (pero no al revés).
• 2) La energía mecánica se puede convertir a energía térmica (pero no al revés).
• 3) Un soluto puede pasar de una región de mayor concentración a una región de menor concentración (pero no al revés).

Sin embargo, para algunos sistemas no aislados que pueden intercambiar energía con su entorno, el entorno intercambia suficiente calor con el sistema o realiza suficiente trabajo en el sistema para que los procesos ocurran en la dirección opuesta. Esto es posible siempre que el cambio de entropía total del sistema más el entorno sea positivo, como exige la segunda ley: ΔS_tot = ΔS + ΔS_R > 0. Para los tres ejemplos dados arriba:

• 1) El calor se puede transferir de una región de menor temperatura a una temperatura más alta en un refrigerador o en una bomba de calor. Estas máquinas deben proporcionar suficiente trabajo al sistema.
• 2) La energía térmica se puede convertir en trabajo mecánico en un motor de calor, si el calor suficiente también es expulsado al entorno.
• 3) Un soluto puede pasar de una región de menor concentración a una región de mayor concentración en el proceso bioquímico del transporte activo, si el trabajo suficiente es proporcionado por un gradiente de concentración de un químico como ATP o por un gradiente electroquímico.

La segunda ley de la termodinámica química

Para un proceso químico espontáneo en un sistema cerrado a temperatura y presión constantes sin trabajo no PV, la desigualdad de Clausius ΔS > Q/T_surr se transforma en una condición para el cambio en la energía libre de Gibbs

${displaystyle Delta G made0}$

o dG 0. Para un proceso similar a temperatura y volumen constantes, el cambio en la energía libre de Helmholtz debe ser negativo, ${displaystyle Delta A made0}$. Así, un valor negativo del cambio en la energía libre (G o A) es una condición necesaria para que un proceso sea espontáneo. Esta es la forma más útil de la segunda ley de la termodinámica en la química, donde los cambios de energía libre se pueden calcular a partir de entalpies tabulados de formación y entropías molares estándar de reaccionarios y productos. La condición de equilibrio químico en constante T y p sin trabajo eléctrico es dG = 0.

Historia

Nicolas Léonard Sadi Carnot en el tradicional uniforme de un estudiante de la Escuela Politécnica

La primera teoría de la conversión de calor en trabajo mecánico se debe a Nicolas Léonard Sadi Carnot en 1824. Fue el primero en darse cuenta correctamente de que la eficiencia de esta conversión depende de la diferencia de temperatura entre un motor y su entorno.

Al reconocer la importancia del trabajo de James Prescott Joule sobre la conservación de la energía, Rudolf Clausius fue el primero en formular la segunda ley durante 1850, de esta forma: el calor no fluye espontáneamente de cuerpos fríos a cuerpos calientes. Si bien ahora es de conocimiento común, esto era contrario a la teoría calórica del calor popular en ese momento, que consideraba el calor como un fluido. De allí pudo inferir el principio de Sadi Carnot y la definición de entropía (1865).

Establecido durante el siglo XIX, el enunciado de la segunda ley de Kelvin-Planck dice: "Es imposible que cualquier dispositivo que opere en un ciclo reciba calor de un solo depósito y produzca una cantidad neta de trabajo". " Se demostró que esto era equivalente a la afirmación de Clausius.

La hipótesis ergódica también es importante para el enfoque de Boltzmann. Dice que, durante largos períodos de tiempo, el tiempo pasado en alguna región del espacio de fase de microestados con la misma energía es proporcional al volumen de esta región, es decir, que todos los microestados accesibles son igualmente probables durante un largo período de tiempo. De manera equivalente, dice que el promedio de tiempo y el promedio sobre el conjunto estadístico son iguales.

Existe una doctrina tradicional, comenzando con Clausius, según la cual la entropía puede entenderse en términos de 'desorden' molecular; dentro de un sistema macroscópico. Esta doctrina es obsoleta.

Cuenta proporcionada por Clausius

Rudolf Clausius

En 1865, el físico alemán Rudolf Clausius declaró lo que llamó el "segundo teorema fundamental en la teoría mecánica del calor" de la siguiente forma:

${displaystyle int {frac {delta Q}=-N}$

donde Q es calor, T es temperatura y N es el "valor de equivalencia" de todas las transformaciones no compensadas involucradas en un proceso cíclico. Posteriormente, en 1865, Clausius vendría a definir "equivalencia-valor" como entropía. Inmediatamente después de esta definición, ese mismo año, se leyó la versión más famosa de la segunda ley en una presentación en la Sociedad Filosófica de Zúrich el 24 de abril, en la que, al final de su presentación, Clausius concluye:

La entropía del universo tiende a un máximo.

Esta afirmación es la redacción más conocida de la segunda ley. Debido a la holgura de su lenguaje, p. universo, así como la falta de condiciones específicas, p. abierto, cerrado o aislado, muchas personas interpretan esta simple afirmación en el sentido de que la segunda ley de la termodinámica se aplica prácticamente a todos los temas imaginables. Esto no es verdad; esta declaración es solo una versión simplificada de una descripción más extensa y precisa.

En términos de variación de tiempo, el enunciado matemático de la segunda ley para un sistema aislado que sufre una transformación arbitraria es:

${displaystyle {frac {dt}}gq 0}$

dónde

S es la entropía del sistema y

t es hora.

El signo de igualdad se aplica después del equilibrio. Una forma alternativa de formular la segunda ley para sistemas aislados es:

${displaystyle {frac {dt}={dot} {S}_{i}$ con ${displaystyle { dot {}_{i}gq 0}$

con ${displaystyle { dot {}_{i}}$ la suma de la tasa de producción de entropía por todos los procesos dentro del sistema. La ventaja de esta formulación es que muestra el efecto de la producción de entropía. La tasa de producción de entropía es un concepto muy importante ya que determina (limita) la eficiencia de las máquinas térmicas. Multiplicado con temperatura ambiente ${displaystyle T_{a}$ da la llamada energía disipada ${displaystyle P_{diss}=T_{a}{dot {S}_{i}$.

La expresión de la segunda ley para sistemas cerrados (es decir, que permiten el intercambio de calor y los límites móviles, pero no el intercambio de materia) es:

${displaystyle {frac {}{dt}={frac} {fnh} {fnh} {fnh} {fnh} {fnh}} {fnh}}} {fnh}}} {fnh}}} {fnh}}} {fnh}}} {fnh}}}} {fnh}}}}}}} { {S}_{i}$ con ${displaystyle { dot {}_{i}gq 0}$

Aquí

${displaystyle { dot {}}}$ es el flujo de calor en el sistema

${displaystyle T}$ es la temperatura en el punto donde el calor entra en el sistema.

El signo de igualdad se cumple en el caso de que solo tengan lugar procesos reversibles dentro del sistema. Si tienen lugar procesos irreversibles (que es el caso de los sistemas reales en funcionamiento), se mantiene el signo >. Si se suministra calor al sistema en varios lugares, tenemos que tomar la suma algebraica de los términos correspondientes.

Para sistemas abiertos (que también permiten el intercambio de materia):

${displaystyle {frac {}{dt}={frac} {fnh} {fnh} {fnh} {fnh} {fnh}} {fnh}}} {fnh}}} {fnh}}} {fnh}}} {fnh}}} {fnh}}}} {fnh}}}}}}} { {S}+{dot {S}_{i}$ con ${displaystyle { dot {}_{i}gq 0}$

Aquí. ${displaystyle { dot {}}}$ es el flujo de entropía en el sistema asociado con el flujo de materia que entra en el sistema. No debe confundirse con el derivado del tiempo de la entropía. Si la materia se suministra en varios lugares tenemos que tomar la suma algebraica de estas contribuciones.

Mecánica estadística

La mecánica estadística da una explicación de la segunda ley al postular que un material está compuesto de átomos y moléculas que están en constante movimiento. Un conjunto particular de posiciones y velocidades para cada partícula en el sistema se denomina microestado del sistema y, debido al movimiento constante, el sistema cambia constantemente su microestado. La mecánica estadística postula que, en equilibrio, cada microestado en el que podría estar el sistema tiene la misma probabilidad de ocurrir, y cuando se hace esta suposición, lleva directamente a la conclusión de que la segunda ley debe cumplirse en un sentido estadístico. Es decir, la segunda ley se cumplirá en promedio, con una variación estadística del orden de 1/√ N donde N es el número de partículas en el sistema. Para situaciones cotidianas (macroscópicas), la probabilidad de que se viole la segunda ley es prácticamente cero. Sin embargo, para sistemas con una pequeña cantidad de partículas, los parámetros termodinámicos, incluida la entropía, pueden mostrar desviaciones estadísticas significativas de lo predicho por la segunda ley. La teoría termodinámica clásica no se ocupa de estas variaciones estadísticas.

Derivación de la mecánica estadística

El primer argumento mecánico de la teoría cinética de los gases de que las colisiones moleculares implican una igualación de temperaturas y, por tanto, una tendencia hacia el equilibrio se debió a James Clerk Maxwell en 1860; Ludwig Boltzmann con su teorema H de 1872 también argumentó que, debido a las colisiones, los gases deberían tender con el tiempo hacia la distribución de Maxwell-Boltzmann.

Debido a la paradoja de Loschmidt, las derivaciones de la Segunda Ley tienen que hacer una suposición con respecto al pasado, es decir, que el sistema no está correlacionado en algún momento del pasado; esto permite un tratamiento probabilístico simple. Esta suposición generalmente se piensa como una condición límite y, por lo tanto, la segunda Ley es, en última instancia, una consecuencia de las condiciones iniciales en algún lugar del pasado, probablemente al comienzo del universo (el Big Bang), aunque también se han sugerido otros escenarios.

Dados estos supuestos, en la mecánica estadística, la Segunda Ley no es un postulado, sino que es una consecuencia del postulado fundamental, también conocido como el mismo postulado de probabilidad anterior, siempre y cuando uno sea claro que los argumentos de probabilidad simple se aplican sólo al futuro, mientras que para el pasado hay fuentes auxiliares de información que nos dicen que era baja entropía. La primera parte de la segunda ley, que afirma que la entropía de un sistema aislado térmicamente sólo puede aumentar, es una consecuencia trivial del mismo postulado de probabilidad anterior, si restringimos la noción de la entropía a los sistemas en equilibrio térmico. La entropía de un sistema aislado en equilibrio térmico que contiene una cantidad de energía ${displaystyle E}$ es:

${displaystyle S=k_{mathrm {B}ln left[Omega left(Eright)right]}$

Donde ${displaystyle Omega left(Eright)}$ es el número de estados cuánticos en un pequeño intervalo entre ${displaystyle E}$ y ${displaystyle E+delta E.$. Aquí. ${displaystyle delta E}$ es un intervalo de energía macroscópicamente pequeño que se mantiene fijo. Strictly speaking this means that the entropy depends on the choice of ${displaystyle delta E}$. Sin embargo, en el límite termodinámico (es decir, en el límite del tamaño del sistema infinitamente grande), la entropía específica (entropía por volumen unitario o por masa unitaria) no depende de ${displaystyle delta E}$.

Supongamos que tenemos un sistema aislado cuyo estado macroscópico es especificado por una serie de variables. Estas variables macroscópicas pueden, por ejemplo, referirse al volumen total, las posiciones de los pistones en el sistema, etc. Entonces... ${displaystyle Omega }$ dependerá de los valores de estas variables. Si una variable no se fija, (por ejemplo, no sujetamos un pistón en una posición determinada), entonces porque todos los estados accesibles son igualmente probables en equilibrio, la variable libre en equilibrio será tal que ${displaystyle Omega }$ se maximiza en la energía dada del sistema aislado, ya que es la situación más probable en el equilibrio.

Si la variable fue fijada inicialmente a algún valor después de la liberación y cuando se ha alcanzado el nuevo equilibrio, el hecho de que la variable se ajustará para que ${displaystyle Omega }$ es maximizado, implica que la entropía habrá aumentado o habrá permanecido el mismo (si el valor en el que la variable fue fijada pasó a ser el valor del equilibrio). Supongamos que empezamos desde una situación de equilibrio y de repente eliminamos una limitación en una variable. Luego justo después de hacer esto, hay un número ${displaystyle Omega }$ de microestados accesibles, pero aún no se ha alcanzado el equilibrio, por lo que las probabilidades reales del sistema que está en algún estado accesible todavía no son iguales a la probabilidad previa de ${displaystyle 1/Omega }$. Ya hemos visto que en el estado del equilibrio final, la entropía habrá aumentado o se ha mantenido igual en relación con el estado del equilibrio anterior. El teorema H de Boltzmann, sin embargo, demuestra que la cantidad H aumenta monotonicamente como función del tiempo durante la salida intermedia del estado del equilibrio.

Derivación del cambio de entropía para procesos reversibles

La segunda parte de la Segunda Ley establece que el cambio de entropía de un sistema que experimenta un proceso reversible está dado por:

${displaystyle dS={frac {delta Q} {T}}$

donde la temperatura se define como:

${displaystyle {frac}{mathrm {B} }T}equiv beta equiv {frac {dln left[Omega left(Eright)} {dE}}}}$

Consulte aquí la justificación de esta definición. Suponga que el sistema tiene algún parámetro externo, x, que se puede cambiar. En general, los estados propios de energía del sistema dependerán de x. De acuerdo con el teorema adiabático de la mecánica cuántica, en el límite de un cambio infinitamente lento del hamiltoniano del sistema, el sistema permanecerá en el mismo estado propio de energía y, por lo tanto, cambiará su energía de acuerdo con el cambio de energía del estado propio de energía. Está dentro.

La fuerza generalizada, X, correspondiente a la variable externa x se define como tal ${displaystyle Xdx}$ es el trabajo realizado por el sistema si x se incrementa por una cantidad dx. Por ejemplo, si x es el volumen, entonces X es la presión. La fuerza generalizada para un sistema conocido por estar en energía eigenstat ${displaystyle E_{r}$ es dado por:

${displaystyle X=-{frac {dE_{r} {dx}}}$

Puesto que el sistema puede estar en cualquier eigenstat de energía dentro de un intervalo de ${displaystyle delta E}$, definimos la fuerza generalizada para el sistema como el valor de expectativa de la expresión anterior:

${displaystyle X=-leftlangle {frac {dE_{r}{dx}rightrangle ,}$

Para evaluar el promedio, partimos el ${displaystyle Omega left(Eright)}$ eigentales energéticos contando cuántos tienen un valor para ${displaystyle {frac {}{dx}} {fn}} {fnK}} {fn}}} {fn}}}} {fn}}}} {fnK}}}}}}}} {fn}}}}}} {f}}}}} {fn}}}}}$ dentro de un rango entre ${displaystyle Sí.$ y ${displaystyle Y+delta Sí.$. Llamando a este número ${displaystyle Omega _{Y}left(Eright)}$, tenemos:

${displaystyle Omega left(Eright)=sum ¿Por qué?$

El promedio que define la fuerza generalizada ahora se puede escribir:

${displaystyle X=-{frac {1}{Omega left(Eright)}sum ¿Por qué?$

Podemos relacionar esto con el derivado de la entropía con respecto a x energía constante E como sigue. Supongamos que cambiamos x a x + dx. Entonces... ${displaystyle Omega left(Eright)}$ cambiará porque los eigentales de energía dependen de x, causando la energía eigentales para entrar o salir del rango entre ${displaystyle E}$ y ${displaystyle E+delta E.$. Volvamos a centrarnos en los eigenstatos energéticos para los cuales ${textstyle {frac {dE_{r} {dx}}}$ yace dentro del rango entre ${displaystyle Sí.$ y ${displaystyle Y+delta Sí.$. Puesto que estos eigentales energéticos aumentan la energía por Y dx, toda esa energía eigentales que están en el intervalo que van desde E – Y dx a E pasar desde abajo E arriba E. Hay

${displaystyle N_{Y}left(Eright)={frac Ydx.$

tales eigentales energéticos. Si ${displaystyle Ydxleq delta E}$, todas estas energías eigentales se moverán en el rango entre ${displaystyle E}$ y ${displaystyle E+delta E.$ y contribuir a un aumento de ${displaystyle Omega }$. El número de eigentales energéticos que se mueven desde abajo ${displaystyle E+delta E.$ arriba ${displaystyle E+delta E.$ es dado por ${displaystyle N_{Y}left(E+delta Eright)}$. La diferencia

${displaystyle N_{Y}left(Eright)-N_{Y}left(E+delta Eright),}$

por lo tanto, la contribución neta al aumento ${displaystyle Omega }$. Note que si Y dx es más grande que ${displaystyle delta E}$ habrá los eigentales energéticos que se mueven desde abajo E arriba ${displaystyle E+delta E.$. Son contados en ambos ${displaystyle N_{Y}left(Eright)}$ y ${displaystyle N_{Y}left(E+delta Eright)}$, por lo tanto, la expresión anterior también es válida en ese caso.

Expresando la expresión anterior como una derivada con respecto a E y sumando sobre Y se obtiene la expresión:

${displaystyle left({frac {partial Omega}{partial x}right)_{E}=-sum - ¿Qué? Omega ¿Por qué?$

El derivado logarítmico ${displaystyle Omega }$ con respecto a x es así dado por:

${displaystyle left({frac {partial ln left(Omega right)}{partial x}right)_{E}=beta X+left({frac {partial X}{partial E}right)_{x}}}}$

El primer término es intensivo, es decir, no escala con el tamaño del sistema. Por el contrario, el último término se escala como el tamaño inverso del sistema y, por lo tanto, desaparecerá en el límite termodinámico. Así hemos encontrado que:

${displaystyle left({frac {partial S}{partial x}right)_{E}={frac {X} {T},}$

Combinando esto con

${displaystyle left({frac {partial S}{partial E}right)_{x}={frac {1} {T},}$

da:

${displaystyle dS=left({frac {partial S}{partial E}right)_{x}dE+left({frac {partial S}{partial x}}right)_{E}dx={frac {frac}{frac}{partial S}}right) {dE} {T}+{frac} {X} {T}dx={frac} {delta Q}{ T},}$

Derivación para sistemas descritos por el conjunto canónico

Si un sistema está en contacto térmico con un baño de calor a alguna temperatura T entonces, en equilibrio, la distribución de probabilidad sobre los valores propios de energía viene dada por el conjunto canónico:

${displaystyle P_{j}={frac {expleft(-{frac {E_{j}{k_{mathrm} {B}T}} {Z}}}$

Aquí Z es un factor que normaliza la suma de todas las probabilidades a 1, esta función se conoce como función de partición. Consideremos ahora un cambio infinitesimal reversible en la temperatura y en los parámetros externos de los que dependen los niveles de energía. De la fórmula general de la entropía se sigue:

${displaystyle S=-k_{mathrm {B}sum _{j}P_{j}ln left(P_{j}right)}$

que

${displaystyle DS=-k_{mathrm {B}sum _{j}lnleft(P_{j}right)dP_{j}$

Insertar la fórmula para ${displaystyle P_{j}$ para el conjunto canónico aquí da:

${displaystyle DS={frac {1}{T}sum} ¿Qué? {1}}sum _{j}dleft(E_{j}P_{j}right)-{frac {1}{T}sum} ¿Por qué? {dE+delta W. T}={frac {delta Q} {T}}$

Condiciones iniciales en el Big Bang

Como se explicó anteriormente, se cree que la segunda ley de la termodinámica es el resultado de las condiciones iniciales de muy baja entropía en el Big Bang. Desde un punto de vista estadístico, se trataba de condiciones muy especiales. Por otro lado, eran bastante simples, ya que el universo, o al menos la parte del mismo a partir de la cual se desarrolló el universo observable, parece haber sido extremadamente uniforme.

Esto puede parecer algo paradójico, ya que en muchos sistemas físicos las condiciones uniformes (por ejemplo, gases mezclados en lugar de separados) tienen una entropía alta. La paradoja se resuelve al darse cuenta de que los sistemas gravitatorios tienen una capacidad calorífica negativa, de modo que cuando la gravedad es importante, las condiciones uniformes (p. ej., gas de densidad uniforme) de hecho tienen una entropía más baja en comparación con las no uniformes (p. ej., agujeros negros en el espacio vacío). Otro enfoque más es que el universo tenía una entropía alta (o incluso máxima) dado su tamaño, pero a medida que el universo creció, salió rápidamente del equilibrio termodinámico, su entropía solo aumentó ligeramente en comparación con el aumento en la entropía máxima posible, y por lo tanto tiene llegó a una entropía muy baja en comparación con el máximo posible mucho mayor dado su tamaño posterior.

En cuanto a la razón por la cual las condiciones iniciales fueron tales, una sugerencia es que la inflación cosmológica fue suficiente para eliminar la falta de suavidad, mientras que otra es que el universo se creó espontáneamente donde el mecanismo de creación implica condiciones iniciales de baja entropía.

Organismos vivos

Hay dos formas principales de formular la termodinámica, (a) a través de pasajes de un estado de equilibrio termodinámico a otro, y (b) a través de procesos cíclicos, por los cuales el sistema permanece sin cambios, mientras que la entropía total del entorno es aumentó. Estas dos formas ayudan a comprender los procesos de la vida. La termodinámica de los organismos vivos ha sido considerada por muchos autores, como Erwin Schrödinger, Léon Brillouin e Isaac Asimov.

En una buena aproximación, los organismos vivos se pueden considerar como ejemplos de (b). Aproximadamente, el estado físico de un animal cambia día a día, dejando al animal casi sin cambios. Los animales toman alimentos, agua y oxígeno y, como resultado del metabolismo, liberan productos de degradación y calor. Las plantas toman energía radiante del sol, que puede considerarse como calor, dióxido de carbono y agua. Dan oxígeno. De esta manera crecen. Eventualmente mueren y sus restos se pudren, convirtiéndose en su mayoría en dióxido de carbono y agua. Esto puede considerarse como un proceso cíclico. En general, la luz solar proviene de una fuente de alta temperatura, el sol, y su energía pasa a un sumidero de temperatura más baja, es decir, se irradia al espacio. Esto es un aumento de la entropía del entorno de la planta. Así, los animales y las plantas obedecen a la segunda ley de la termodinámica, considerada en términos de procesos cíclicos.

Además, la capacidad de los organismos vivos para crecer y aumentar en complejidad, así como para formar correlaciones con su entorno en forma de adaptación y memoria, no se opone a la segunda ley, sino que es similar a los resultados generales. siguiente: Según algunas definiciones, un aumento de la entropía también da como resultado un aumento de la complejidad, y para un sistema finito que interactúa con reservorios finitos, un aumento de la entropía es equivalente a un aumento de las correlaciones entre el sistema y los reservorios.

Los organismos vivos pueden considerarse sistemas abiertos, porque la materia entra y sale de ellos. Actualmente, la termodinámica de los sistemas abiertos se considera a menudo en términos de pasos de un estado de equilibrio termodinámico a otro, o en términos de flujos en la aproximación del equilibrio termodinámico local. El problema de los organismos vivos puede simplificarse aún más mediante la aproximación de suponer un estado estacionario con flujos invariables. Los principios generales de producción de entropía para tales aproximaciones están sujetos a un debate o investigación actual sin resolver.

Sistemas gravitacionales

Por lo general, los sistemas para los que la gravedad no es importante tienen una capacidad calorífica positiva, lo que significa que su temperatura aumenta con su energía interna. Por lo tanto, cuando la energía fluye de un objeto de alta temperatura a un objeto de baja temperatura, la temperatura de la fuente disminuye mientras que la temperatura del sumidero aumenta; por lo tanto, las diferencias de temperatura tienden a disminuir con el tiempo.

Este no siempre es el caso de los sistemas en los que la fuerza gravitatoria es importante: los sistemas que están limitados por su propia gravedad, como las estrellas, pueden tener capacidades caloríficas negativas. A medida que se contraen, tanto su energía total como su entropía disminuyen, pero su temperatura interna puede aumentar. Esto puede ser significativo para las protoestrellas e incluso para los planetas gigantes gaseosos como Júpiter. Sin embargo, cuando se incluye la entropía de la radiación de cuerpo negro emitida por los cuerpos, se puede demostrar que la entropía total del sistema aumenta incluso cuando la entropía del planeta o estrella disminuye.

Como la gravedad es la fuerza más importante que opera en escalas cosmológicas, puede ser difícil o imposible aplicar la segunda ley al universo como un todo.

Estados de no equilibrio

La teoría de la termodinámica clásica o de equilibrio está idealizada. Un postulado o suposición principal, a menudo ni siquiera establecido explícitamente, es la existencia de sistemas en sus propios estados internos de equilibrio termodinámico. En general, una región del espacio que contiene un sistema físico en un momento dado, que se puede encontrar en la naturaleza, no está en equilibrio termodinámico, leído en los términos más estrictos. En términos más generales, nada en todo el universo está o nunca ha estado verdaderamente en equilibrio termodinámico exacto.

Para fines de análisis físico, a menudo es bastante conveniente hacer una suposición de equilibrio termodinámico. Tal suposición puede basarse en prueba y error para su justificación. Si la suposición está justificada, a menudo puede ser muy valiosa y útil porque pone a disposición la teoría de la termodinámica. Los elementos de la suposición de equilibrio son que se observa que un sistema no cambia durante un tiempo indefinidamente largo y que hay tantas partículas en un sistema que su naturaleza de partículas puede ignorarse por completo. Bajo tal suposición de equilibrio, en general, no hay fluctuaciones detectables macroscópicamente. Hay una excepción, el caso de los estados críticos, que exhiben a simple vista el fenómeno de la opalescencia crítica. Para estudios de laboratorio de estados críticos, se necesitan tiempos de observación excepcionalmente largos.

En todos los casos, la suposición de equilibrio termodinámico, una vez hecha, implica como consecuencia que ningún candidato putativo de "fluctuación" altera la entropía del sistema.

Puede suceder fácilmente que un sistema físico presente cambios macroscópicos internos lo suficientemente rápidos como para invalidar la suposición de la constancia de la entropía. O que un sistema físico tiene tan pocas partículas que la naturaleza de las partículas se manifiesta en fluctuaciones observables. Entonces se debe abandonar la suposición de equilibrio termodinámico. No existe una definición general no calificada de entropía para estados de no equilibrio.

Hay casos intermedios, en los que la suposición de equilibrio termodinámico local es una muy buena aproximación, pero estrictamente hablando sigue siendo una aproximación, no teóricamente ideal.

Para situaciones de no equilibrio en general, puede ser útil considerar definiciones mecánicas estadísticas de otras cantidades que pueden llamarse convenientemente 'entropía', pero no deben confundirse ni confundirse con la entropía termodinámica correctamente definida. por la segunda ley. Estas otras cantidades pertenecen de hecho a la mecánica estadística, no a la termodinámica, el dominio primario de la segunda ley.

La física de las fluctuaciones observables macroscópicamente está más allá del alcance de este artículo.

Flecha del tiempo

La segunda ley de la termodinámica es una ley física que no es simétrica a la inversión de la dirección del tiempo. Esto no entra en conflicto con las simetrías observadas en las leyes fundamentales de la física (particularmente la simetría CPT) ya que la segunda ley se aplica estadísticamente en condiciones de frontera asimétricas en el tiempo. La segunda ley se ha relacionado con la diferencia entre avanzar y retroceder en el tiempo, o con el principio de que la causa precede al efecto (la flecha causal del tiempo, o causalidad).

Irreversibilidad

La irreversibilidad en los procesos termodinámicos es una consecuencia del carácter asimétrico de las operaciones termodinámicas, y no de ninguna propiedad microscópica internamente irreversible de los cuerpos. Las operaciones termodinámicas son intervenciones externas macroscópicas impuestas a los cuerpos participantes, no derivadas de sus propiedades internas. Hay reputadas "paradojas" que surgen de no reconocer esto.

La paradoja de Loschmidt

La paradoja de Loschmidt, también conocida como la paradoja de la reversibilidad, es la objeción de que no debería ser posible deducir un proceso irreversible de la dinámica simétrica en el tiempo que describe la evolución microscópica de un sistema macroscópico.

En opinión de Schrödinger, "ahora es bastante obvio de qué manera hay que reformular la ley de la entropía o, para el caso, todas las demás declaraciones irreversibles para que puedan derivarse de reversibles. modelos No debe hablarse de un sistema aislado sino por lo menos de dos, que por el momento puede considerar aislados del resto del mundo, pero no siempre entre sí." Los dos sistemas quedan aislados entre sí por la pared, hasta que ésta es eliminada por la operación termodinámica, como prevé la ley. La operación termodinámica se impone externamente, no sujeta a las leyes dinámicas microscópicas reversibles que gobiernan los constituyentes de los sistemas. Es la causa de la irreversibilidad. La declaración de la ley en el presente artículo cumple con el consejo de Schrödinger. La relación causa-efecto es lógicamente anterior a la segunda ley, no derivada de ella.

Teorema de recurrencia de Poincaré

El teorema de recurrencia de Poincaré considera una descripción microscópica teórica de un sistema físico aislado. Esto puede considerarse como un modelo de un sistema termodinámico después de que una operación termodinámica haya eliminado una pared interna. El sistema, después de un tiempo suficientemente largo, volverá a un estado microscópicamente definido muy cercano al inicial. El tiempo de recurrencia de Poincaré es el tiempo transcurrido hasta el regreso. Es extremadamente largo, probablemente más largo que la vida del universo, y depende en gran medida de la geometría de la pared que fue eliminada por la operación termodinámica. El teorema de recurrencia puede percibirse como una aparente contradicción con la segunda ley de la termodinámica. Más obviamente, sin embargo, es simplemente un modelo microscópico de equilibrio termodinámico en un sistema aislado formado por la eliminación de una pared entre dos sistemas. Para un sistema termodinámico típico, el tiempo de recurrencia es tan grande (muchas veces más largo que el tiempo de vida del universo) que, a todos los efectos prácticos, no se puede observar la recurrencia. Uno podría desear, sin embargo, imaginar que uno podría esperar la recurrencia de Poincaré y luego volver a insertar la pared que fue eliminada por la operación termodinámica. Es entonces evidente que la apariencia de irreversibilidad se debe a la absoluta imprevisibilidad de la recurrencia de Poincaré dado que el estado inicial era de equilibrio termodinámico, como es el caso de la termodinámica macroscópica. Incluso si uno pudiera esperar, no tiene ninguna posibilidad práctica de elegir el instante adecuado para volver a insertar la pared. El teorema de recurrencia de Poincaré proporciona una solución a la paradoja de Loschmidt. Si un sistema termodinámico aislado pudiera ser monitoreado en múltiplos cada vez mayores del tiempo de recurrencia promedio de Poincaré, el comportamiento termodinámico del sistema se volvería invariable bajo la inversión del tiempo.

James Clerk Maxwell

El demonio de Maxwell

James Clerk Maxwell imaginó un contenedor dividido en dos partes, A y B. Ambas partes se llenan con el mismo gas a la misma temperatura y se colocan una al lado de la otra, separadas por una pared. Al observar las moléculas en ambos lados, un demonio imaginario guarda una trampilla microscópica en la pared. Cuando una molécula más rápida que el promedio de A vuela hacia la trampilla, el demonio la abre y la molécula volará de A a B. La velocidad promedio de las moléculas en B habrá aumentado mientras que en A habrán disminuido en promedio. Dado que la velocidad molecular promedio corresponde a la temperatura, la temperatura disminuye en A y aumenta en B, contrariamente a la segunda ley de la termodinámica.

Una respuesta a esta pregunta fue sugerida en 1929 por Leó Szilárd y luego por Léon Brillouin. Szilárd señaló que un demonio de Maxwell de la vida real necesitaría tener algún medio para medir la velocidad molecular, y que el acto de adquirir información requeriría un gasto de energía. Asimismo, Brillouin demostró que la disminución de entropía provocada por el demonio sería menor que la entropía producida al elegir moléculas en función de su velocidad.

El 'demonio' de Maxwell altera repetidamente la permeabilidad de la pared entre A y B. Por lo tanto, está realizando operaciones termodinámicas a escala microscópica, no solo observando procesos termodinámicos macroscópicos naturales o espontáneos ordinarios.

Citas

La ley que entropía siempre aumenta sostiene, creo, la posición suprema entre las leyes de la Naturaleza. Si alguien te señala que tu teoría de mascotas del universo está en desacuerdo con las ecuaciones de Maxwell, entonces mucho peor para las ecuaciones de Maxwell. Si se descubre que es contradictorio por la observación – bien, estos experimentalistas a veces se desangran las cosas. Pero si tu teoría se encuentra en contra de la segunda ley de la termodinámica no puedo darles esperanza; no hay nada para ello sino para colapsar en la humillación más profunda.

—Sir Arthur Stanley Eddington, La naturaleza del mundo físico (1927)

Ha habido casi tantas formulaciones de la segunda ley como se ha discutido.

—Filosofía / Fisicista P.W. Bridgman, (1941)

Clausius es el autor de la declaración sibilónica, "La energía del universo es constante; la entropía del universo tiende a un máximo." Los objetivos de la termomecánica continua se detienen lejos de explicar el "universo", pero dentro de esa teoría podemos fácilmente derivar una declaración explícita de alguna manera que recuerda a Clausius, pero refiriéndose sólo a un objeto modesto: un cuerpo aislado de tamaño finito.

—Truesdell, C., Muncaster, R. G. (1980). Fundamentos de la teoría cinética de Maxwell de un gas monotómico simple, tratados como una rama de la mecánica racional, Academic Press, New York, ISBN 0-12-701350-4, p. 17.