Salto hidraulico

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Descarga de líquido de alta velocidad en área de baja velocidad

Figura 1: Una balsa que encuentra un salto hidráulico en Canolfan Tryweryn en Gales.

Un salto hidráulico es un fenómeno en la ciencia de la hidráulica que se observa con frecuencia en el flujo de canales abiertos como ríos y vertederos. Cuando un líquido a alta velocidad se descarga en una zona de menor velocidad, se produce un ascenso bastante abrupto en la superficie del líquido. El líquido que fluye rápidamente se ralentiza abruptamente y aumenta de altura, convirtiendo parte de la energía cinética inicial del flujo en un aumento de la energía potencial, y parte de la energía se pierde irreversiblemente a través de la turbulencia en calor. En un flujo de canal abierto, esto se manifiesta como un flujo rápido que se desacelera rápidamente y se acumula sobre sí mismo de manera similar a como se forma una onda de choque.

Leonardo da Vinci lo observó y documentó por primera vez en el siglo XVI. Las matemáticas fueron descritas por primera vez por Giorgio Bidone de la Universidad de Turín cuando publicó un artículo en 1820 llamado Experiences sur le remou et sur la propagation des ondes.

El fenómeno depende de la velocidad inicial del fluido. Si la velocidad inicial del fluido está por debajo de la velocidad crítica, entonces no es posible el salto. Para velocidades de flujo iniciales que no están significativamente por encima de la velocidad crítica, la transición aparece como una onda ondulante. A medida que la velocidad del flujo inicial aumenta aún más, la transición se vuelve más abrupta, hasta que a velocidades lo suficientemente altas, el frente de transición se romperá y se enroscará sobre sí mismo. Cuando esto sucede, el salto puede ir acompañado de turbulencias violentas, remolinos, arrastre de aire y ondulaciones superficiales u olas.

Hay dos manifestaciones principales de saltos hidráulicos e históricamente se ha utilizado una terminología diferente para cada uno. Sin embargo, los mecanismos detrás de ellos son similares porque son simplemente variaciones entre sí vistas desde diferentes marcos de referencia, por lo que la física y las técnicas de análisis pueden usarse para ambos tipos.

Las diferentes manifestaciones son:

El salto hidráulico estacionario – rápido flujo de agua transiciones en un salto estacionario al agua que mueve lentamente como se muestra en las Figuras 1 y 2.
El mineral de marea – una pared o ondulada onda de agua se mueve río arriba contra el agua que fluye hacia abajo como se muestra en las Figuras 3 y 4. Si uno considera un marco de referencia que se mueve junto con el frente de onda, entonces el frente de onda es estacionario relativo al marco y tiene el mismo comportamiento esencial que el salto estacionario.

Un caso relacionado es una cascada: una pared o una ola ondulante de agua se mueve río abajo superando un flujo de agua río abajo menos profundo, como se muestra en la Figura 5. Si se considera desde un marco de referencia que se mueve con el frente de onda, esto es susceptible de el mismo análisis que un salto estacionario.

Estos fenómenos se abordan en una extensa literatura desde varios puntos de vista técnicos.

El salto hidráulico se usa a veces para mezclar productos químicos.

Clases de saltos hidráulicos

Figura 3: Un tidal bore en Alaska mostrando un turbulento frente de onda de choque. En este punto el agua es relativamente poco profunda y el cambio fraccional en la elevación es grande.

Los saltos hidráulicos se pueden ver tanto en forma estacionaria, que se conoce como "salto hidráulico", como en forma dinámica o en movimiento, que se conoce como oleada positiva o "salto hidráulico en traducción". Pueden describirse utilizando los mismos enfoques analíticos y son simplemente variantes de un solo fenómeno.

Salto hidráulico en movimiento

Una perforación de marea es un salto hidráulico que ocurre cuando la marea entrante forma una ola (u olas) de agua que ascienden por un río o una bahía estrecha en contra de la dirección de la corriente. Como ocurre con los saltos hidráulicos en general, las perforaciones toman varias formas dependiendo de la diferencia en el nivel del agua aguas arriba y aguas abajo, que van desde un frente de onda ondular hasta una pared de agua similar a una onda de choque. La Figura 3 muestra una perforación de marea con las características comunes a las aguas poco profundas río arriba: se observa una gran diferencia de elevación. La figura 4 muestra una perforación de marea con las características comunes a las aguas profundas aguas arriba: se observa una pequeña diferencia de elevación y el frente de onda ondula. En ambos casos, el maremoto se mueve a la velocidad característica de las olas en el agua de la profundidad que se encuentra inmediatamente detrás del frente de onda. Una característica clave de las perforaciones de marea y las oleadas positivas es la intensa mezcla turbulenta inducida por el paso del frente de perforación y por el siguiente movimiento de onda.

Otra variación del salto hidráulico en movimiento es la cascada. En la cascada, una serie de ondas onduladas u onduladas de agua se mueve río abajo superando un flujo de agua aguas abajo menos profundo.

Un salto hidráulico en movimiento se llama oleada. El viaje de la onda es más rápido en la parte superior que en la parte inferior en caso de sobretensiones positivas

Salto hidráulico estacionario

Un salto hidráulico estacionario es el tipo visto con mayor frecuencia en los ríos y en las características de ingeniería tales como emisarios de presas y obras de riego. Ocurren cuando un flujo de líquido a alta velocidad se descarga en una zona del río o en una estructura diseñada que solo puede soportar una velocidad más baja. Cuando esto ocurre, el agua se desacelera en un ascenso bastante abrupto (un escalón u onda estacionaria) en la superficie del líquido.

Comparando las características antes y después, se encuentra:

**Descriptivo hidráulico Características del salto**
Características	Antes del salto	Después del salto
Velocidad de líquido	supercrítica (más rápido que la velocidad de onda) también conocida como disparo o superundal	subcrítica también conocida como tranquila o subundal
Altura de líquido	bajo	alto
flujo	típicamente suave turbulento	típicamente flujo turbulento (rough and choppy)

El otro salto hidráulico estacionario ocurre cuando un flujo rápido se encuentra con un objeto sumergido que lanza el agua hacia arriba. Las matemáticas detrás de esta forma son más complejas y deberán tener en cuenta la forma del objeto y las características de flujo del fluido que lo rodea.

Análisis del salto hidráulico sobre una superficie líquida

Salto hidráulico naturalmente observado en el canal norte de Caídas de Spokane.

A pesar de la aparente complejidad de la transición del flujo, la aplicación de herramientas analíticas simples a un análisis bidimensional es eficaz para proporcionar resultados analíticos que se asemejan mucho a los resultados de campo y de laboratorio. El análisis muestra:

Altura del salto: la relación entre las profundidades antes y después del salto como función del caudal
Pérdida energética en el salto
Ubicación del salto en una estructura natural o de ingeniería
Carácter del salto: undular o abrupto

Altura del salto

La altura del salto se deriva de la aplicación de las ecuaciones de conservación de la masa y el momento. Existen varios métodos para predecir la altura de un salto hidráulico.

Todos llegan a conclusiones comunes de que:

La relación de la profundidad del agua antes y después del salto depende únicamente de la relación de velocidad del agua que entra en el salto a la velocidad de la onda que supera el agua en movimiento.
La altura del salto puede ser muchas veces la profundidad inicial del agua.

Para una tasa de flujo conocida $q,$ como muestra la figura abajo, la aproximación de que el flujo de impulso es el mismo justo arriba y abajo del principio de energía produce una expresión de la pérdida de energía en el salto hidráulico. Los saltos hidráulicos se utilizan comúnmente como disipadores de energía río abajo de los vertederos de presa.

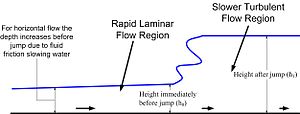
Ilustración del comportamiento en un salto hidráulico.

Aplicación del principio de continuidad

En la dinámica de fluidos, la ecuación de continuidad es efectivamente una ecuación de conservación de masa. Considerando cualquier superficie cerrada fija dentro de un fluido de movimiento incompresible, el fluido fluye hacia un volumen dado en algunos puntos y fluye hacia fuera en otros puntos a lo largo de la superficie sin cambio neto en masa dentro del espacio ya que la densidad es constante. En el caso de un canal rectangular, luego la igualdad de flujo de masa río arriba ( $rho v_{0}h_{0}$ ) y aguas abajo ( $rho v_{1}h_{1}$ ) da:

v_{0}h_{0}=v_{1}h_{1}=q

{displaystyle v_{1}=v_{0}{h_{0} over h_{1}},}

con $rho$ la densidad del fluido, $v_{0}$ y $v_{1}$ las velocidades de flujo mediadas de profundidad, aguas arriba y abajo, y $h_{0}$ y $h_{1}$ las profundidades de agua correspondientes.

Conservación del flujo de impulso

Para un canal rectangular prismático recto, la conservación del flujo de cantidad de movimiento a lo largo del salto, suponiendo una densidad constante, se puede expresar como:

{displaystyle rho v_{0}^{2}h_{0}+{1 over 2}rho gh_{0}^{2}=rho v_{1}^{2}h_{1}+{1 over 2}rho gh_{1}^{2}.}

En canales rectangulares, dicha ecuación de conservación se puede simplificar aún más a la forma de ecuación M-y adimensional, que se usa ampliamente en el análisis de salto hidráulico en el flujo de canales abiertos.

Altura de salto en términos de flujo Dividir por constante $rho$ e introducir el resultado de la continuidad da

v_{0}^{2}left(h_{0}-{h_{0}^{2} over h_{1}}right)+{g over 2}(h_{0}^{2}-h_{1}^{2})=0.

que, después de un poco de álgebra, se simplifica a:

{1 over 2}{h_{1} over h_{0}}left({h_{1} over h_{0}}+1right)-Fr^{2}=0,

Donde $Fr^{2}={v_{0}^{2} over gh_{0}}.$ Aquí. $Fr$ es el número Froude sin dimensión, y se relaciona inercial con las fuerzas gravitatorias en el flujo de corriente. Resolver este rendimiento cuadrático:

{displaystyle {h_{1} over h_{0}}={frac {-1pm {sqrt {1+{frac {8v_{0}^{2}}{gh_{0}}}}}}{2}}.}

Las respuestas negativas no producen soluciones físicas significativas, por lo que esto se reduce a:

{displaystyle {h_{1} over h_{0}}={frac {-1+{sqrt {1+{frac {8v_{0}^{2}}{gh_{0}}}}}}{2}}}

Así que...

{displaystyle {h_{1} over h_{0}}={frac {{sqrt {1+{8Fr^{2}}}}-1}{2}},}

conocida como ecuación de Bélanger. El resultado puede extenderse a una sección transversal irregular.

Esto produce tres clases de solución:

Cuando ${displaystyle {frac {v_{0}^{2}}{gh_{0}}}=1}$ , entonces ${h_{1} over h_{0}}=1$ (es decir, no hay salto)
Cuando $<math alttext="{displaystyle {frac {v_{0}^{2}}{gh_{0}}}v02gh0.1{fnMicroc} [V_{0} {2} {0} {0}} {0}} {0}}} {0}}}}}} {c}}}} {c}}}}}}} {c}}}}}}}}}} {c}} {}}}}}}} {}}}}} {}}}}}}}} {}}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}} {c}}}}}}}}}}}} {c}}}}}}}}}}}<img alt="{displaystyle {frac {v_{0}^{2}}{gh_{0}}}$ , entonces $<math alttext="{displaystyle {h_{1} over h_{0}}h1h0.1{displaystyle {h_{1} over - ¿Qué?<img alt="{h_{1} over h_{0}}$ (es decir, hay un salto negativo – esto se puede mostrar como no conservar la energía y sólo es físicamente posible si alguna fuerza era para acelerar el líquido en ese momento)
Cuando $1}" xmlns="http://www.w3.org/1998/Math/MathML">v02gh0■1{fnMicroc} {fnK}} {fn}}}}}} {fn}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a7c0abc61d24541cfba461bc5d8ff30ab7fffb9b" style="vertical-align: -2.338ex; width:8.606ex; height:6.509ex;"/>$ , entonces $1}" xmlns="http://www.w3.org/1998/Math/MathML">h1h0■1{displaystyle {h_{1} over ¿Qué?1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c1b9e39e4ac006263ef2c636340441877d7de1f4" style="vertical-align: -2.338ex; width:7.49ex; height:5.843ex;"/>$ (es decir, hay un salto positivo)

Esto equivale a la condición de que $1}" xmlns="http://www.w3.org/1998/Math/MathML">Fr■1{displaystyle Fr título1}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9a7fd31b20d138f9549d7d160aa728b95abd5e15" style="vertical-align: -0.338ex; width:7.631ex; height:2.176ex;"/>$ . Desde ${sqrt {gh_{0}}}$ es la velocidad de una onda de gravedad poco profunda, la condición de que $1}" xmlns="http://www.w3.org/1998/Math/MathML">Fr■1{displaystyle Fr título1}1}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9a7fd31b20d138f9549d7d160aa728b95abd5e15" style="vertical-align: -0.338ex; width:7.631ex; height:2.176ex;"/>$ es equivalente a afirmar que la velocidad inicial representa flujo supercrítico (número de fraude 1) mientras que la velocidad final representa el flujo subcrítico (Número de fraude Identificado 1).

Undulations downstream of the jump

Prácticamente, esto significa que el agua acelerada por grandes gotas puede crear ondas estacionarias más fuertes (perforaciones onduladas) en forma de saltos hidráulicos a medida que se desacelera en la base de la gota. Tales ondas estacionarias, cuando se encuentran aguas abajo de un vertedero o saliente de roca natural, pueden formar un "guardián" con un muro de agua que "mantiene" objetos flotantes (p. ej., troncos, kayaks o kayakistas) que recirculan en la onda estacionaria durante períodos prolongados.

Disipación de energía por salto hidráulico

Una de las aplicaciones de ingeniería más importantes del salto hidráulico es disipar energía en canales, aliviaderos de presas y estructuras similares para que el exceso de energía cinética no dañe estas estructuras. La tasa de disipación de energía o pérdida de carga a través de un salto hidráulico es una función del número de Froude del flujo de entrada del salto hidráulico y la altura del salto.

La pérdida de energía en un salto hidráulico expresada como pérdida de carga es:

${displaystyle Delta E={frac {(h_{1}-h_{0})^{3}}{4h_{0}h_{1}}}}$

Ubicación del salto hidráulico en el lecho de un río o en una estructura de ingeniería

En el diseño de una represa, la energía de la corriente que fluye rápidamente sobre un aliviadero debe disiparse parcialmente para evitar la erosión del lecho del río aguas abajo del aliviadero, lo que en última instancia podría provocar la falla de la represa. Esto se puede hacer disponiendo la formación de un salto hidráulico para disipar la energía. Para limitar el daño, este salto hidráulico normalmente se produce en una plataforma diseñada para resistir las fuerzas hidráulicas y evitar la cavitación local y otros fenómenos que aceleran la erosión.

En el diseño de un aliviadero y plataforma, los ingenieros seleccionan el punto en el que ocurrirá un salto hidráulico. Las obstrucciones o los cambios de pendiente se diseñan de forma rutinaria en la plataforma para forzar un salto en una ubicación específica. Las obstrucciones son innecesarias, ya que el cambio de pendiente por sí solo suele ser suficiente. Para activar el salto hidráulico sin obstáculos, se diseña una plataforma de modo que la pendiente plana de la plataforma retarde el flujo rápido de agua desde el vertedero. Si la pendiente de la plataforma es insuficiente para mantener la alta velocidad original, se producirá un salto.

Flujo supercrítico por el derrame de la presa de Cleveland en la cabeza del río Capilano en North Vancouver, Columbia Británica, Canadá.

Dos métodos para diseñar un salto inducido son comunes:

Si el flujo de aguas abajo está restringido por el canal de aguas abajo de tal manera que el agua retrocede al pie del derrame, que el nivel de aguas abajo se puede utilizar para identificar la ubicación del salto.
Si el derrame sigue bajando por cierta distancia, pero la pendiente cambia tal que ya no soportará el flujo supercrítico, la profundidad en la región de flujo subcrítico inferior es suficiente para determinar la ubicación del salto.

En ambos casos, la profundidad final del agua se determina por las características de aguas abajo. El salto ocurrirá si y sólo si el nivel de afluencia (supercrítico) nivel de agua ( $h_{0}$ ) satisface la condición:

{displaystyle h_{0}={h_{1} over 2}left({-1+{sqrt {1+8Fr_{2}^{2}}}}right)}

$Fr$ = Número de Froude de corriente

g = aceleración debido a la gravedad (esencialmente constante para este caso)

h = altura del líquido (

h_{0}

= altura inicial mientras

h_{1}

= altura de arriba)

Arrastre de aire en saltos hidráulicos

El salto hidráulico se caracteriza por un flujo altamente turbulento. Los vórtices de macroescala se desarrollan en el rodillo de salto e interactúan con la superficie libre conduciendo a la formación de burbujas de aire, salpicaduras y gotitas en la región de flujo de dos fases. El flujo de aire y agua está asociado con la turbulencia, que también puede conducir al transporte de sedimentos. La turbulencia puede verse fuertemente afectada por la dinámica de la burbuja. Físicamente, los mecanismos involucrados en estos procesos son complejos.

El arrastre de aire se produce en forma de burbujas de aire y paquetes de aire atrapados en la incidencia del flujo del chorro aguas arriba con el rodillo. Los paquetes de aire se rompen en burbujas de aire muy pequeñas a medida que se arrastran en la región de cizallamiento, que se caracteriza por un gran contenido de aire y tasas máximas de conteo de burbujas. Una vez que las burbujas arrastradas son advectadas hacia regiones de menor cizallamiento, las colisiones de burbujas y la coalescencia conducen a entidades de aire más grandes que son impulsadas hacia la superficie libre por una combinación de flotabilidad y advección turbulenta.

Resumen tabular de las conclusiones analíticas

**Características del salto hidráulico**
El flujo de corriente ascendente es supercrítico (es decir, el número de Froude prejump)	Relación de altura tras altura antes de saltar	Características descriptivas de salto	Fracción de energía disipada por salto
≤ 1.0	1.0	Sin salto; el flujo debe ser supercrítico para saltar a ocurrir	ninguno
1.0–1.7	1.0-2,0	Onda permanente o ondulante	0,5
1.7–2.5	2.0–3.1	Salto débil (serie de pequeños rodillos)	5% - 15%
2.5 a 4,5	3.1–5.9	Salto oscilante	15% – 45%
4.5–9.0	5.9 a 12,0	Salto estable claramente definido bien equilibrado	45% – 70%
■ 9.0	■ 12.0	Claramente definido, turbulento, fuerte salto	70% – 85%

NB: la clasificación anterior es muy aproximada. Se han observado saltos hidráulicos ondulados con números de Froude de entrada/presalto de hasta 3,5 a 4.

Variaciones de salto hidráulico

Una serie de variaciones son susceptibles de un análisis similar:

Saltos hidráulicos fluidos poco profundos

El salto hidráulico en un lavabo

La Figura 2 anterior ilustra un ejemplo de un salto hidráulico, que a menudo se ve en un fregadero de cocina. Alrededor del lugar donde el agua del grifo llega al fregadero, se producirá un patrón de flujo de aspecto suave. Un poco más lejos, un repentino "salto" en el nivel del agua estará presente. Este es un salto hidráulico.

Al chocar un chorro de líquido normalmente sobre una superficie, el líquido se esparce radialmente en una película delgada hasta un punto donde el espesor de la película cambia abruptamente. Este cambio abrupto en el espesor de la película líquida se denomina salto hidráulico circular. La mayoría de los artículos en la literatura asumen que los saltos hidráulicos de película delgada se crean debido a la gravedad (relacionados con el número de Froude). Sin embargo, un estudio científico reciente cuestionó esta creencia centenaria. Los autores investigaron experimental y teóricamente la posibilidad de que se crearan saltos hidráulicos en el fregadero de la cocina debido a la tensión superficial en lugar de la gravedad. Para descartar el papel de la gravedad en la formación de un salto hidráulico circular, los autores realizaron experimentos en superficies horizontales, verticales e inclinadas y demostraron que, independientemente de la orientación del sustrato, para el mismo caudal y propiedades físicas del líquido, el salto hidráulico inicial ocurre en el mismo lugar. Propusieron un modelo para el fenómeno y encontró que el criterio general para un salto hidráulico de película delgada es

{displaystyle {frac {1}{We}}+{frac {1}{Fr^{2}}}=1}

Donde ${displaystyle We}$ es el número local de Weber y $Fr$ es el número de Froude local. Para los saltos hidráulicos de la escala de la cocina, el número Froude sigue siendo alto, por lo tanto, los criterios eficaces para el salto hidráulico de la película delgada es ${displaystyle We=1}$ . En otras palabras, se produce un salto hidráulico de película delgada cuando el impulso líquido por ancho de unidad equivale a la tensión superficial del líquido. Sin embargo, este modelo se mantiene muy disputado.

Saltos hidráulicos de onda interna

Saltos hidráulicos en formación de abanico abisal

Las corrientes de turbidez pueden dar lugar a saltos hidráulicos internos (es decir, saltos hidráulicos como ondas internas en fluidos de diferente densidad) en la formación de abanicos abisales. Los saltos hidráulicos internos se han asociado con la estratificación inducida por la salinidad o la temperatura, así como con las diferencias de densidad debido a los materiales en suspensión. Cuando la pendiente del lecho (sobre el cual fluye la corriente de turbidez) se aplana, la tasa de flujo más lenta se refleja en una mayor deposición de sedimentos debajo del flujo, lo que produce una pendiente hacia atrás gradual. Cuando ocurre un salto hidráulico, la firma es una abrupta pendiente hacia atrás, que corresponde a la rápida reducción del caudal en el punto del salto.

Saltos hidráulicos atmosféricos

Los saltos hidráulicos ocurren en la atmósfera en el aire que fluye sobre las montañas. También se produce un salto hidráulico en la interfaz de la tropopausa entre la estratosfera y la troposfera a favor del viento de la parte superior de las supercélulas muy fuertes. Una situación relacionada es la nube Morning Glory observada, por ejemplo, en el norte de Australia, a veces llamada salto ondular.

Aplicaciones industriales y recreativas para saltos hidráulicos

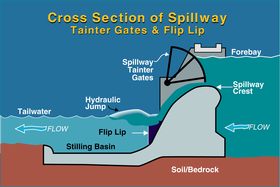
Industrial

El salto hidráulico es la opción más utilizada por los ingenieros de diseño para la disipación de energía por debajo de los aliviaderos y desagües. Un salto hidráulico diseñado correctamente puede proporcionar una disipación de energía del 60-70% de la energía en la cuenca misma, lo que limita el daño a las estructuras y al lecho del río. Incluso con una disipación de energía tan eficiente, los recipientes amortiguadores deben diseñarse cuidadosamente para evitar daños graves debido al levantamiento, la vibración, la cavitación y la abrasión. Se ha desarrollado una extensa literatura para este tipo de ingeniería.

Recreativo

Mientras viajan río abajo, los remeros de kayak y canoa a menudo se detienen y juegan con botes en olas estacionarias y saltos hidráulicos. Las ondas estacionarias y los frentes de choque de los saltos hidráulicos son lugares populares para tal recreación.

Del mismo modo, se sabe que los kayakistas y los surfistas montan en las mareas de los ríos.

Los pilotos de planeadores han utilizado saltos hidráulicos en los Andes y los Alpes y para montar efectos Morning Glory en Australia.

Referencias y notas

^ "El fenómeno household observado por Leonardo da Vinci finalmente explicó". Retrieved 2018-08-08.
^ Cabrera, Enrique (2010). Ingeniería y gestión del agua a través del tiempo: Aprender de la historia. CRC Prensa. ISBN 978-0415480024.
^ a b Douglas, J.F.; Gasiorek, J.M.; Swaffield, J.A. (2001). Mecánica Fluida (4a edición). Essex: Prentice Hall. ISBN 978-0-582-41476-1.
^ a b Faber, T.E. (1995). Dinámica Fluida para Médicos. Cambridge: Cambridge University Press. ISBN 978-0-521-42969-6.
^ a b Faulkner, L.L. (2000). Mecánica Fluida Práctica para Aplicaciones de Ingeniería. Basil, Suiza: Marcel Dekker AG. ISBN 978-0-8247-9575-7.
^ a b Fox, R.W.; McDonald, A.T. (1985). Introducción a la mecánica fluida. John Wiley & Sons. ISBN 978-0-471-88598-6.
^ a b c d Hager, Willi H. (1995). Disipadores de energía y salto hidráulico. Dordrecht: Kluwer Academic Publishers. ISBN 978-90-5410-198-7.
^ a b c d Khatsuria, R.M. (2005). Hidraulics of Spillways and Energy Dissipaters. Nueva York: Marcel Dekker. ISBN 978-0-8247-5789-2.
^ a b Lighthill, James (1978). Olas en fluidos. Cambridge: Cambridge University Press. ISBN 978-0-521-29233-7.
^ a b Roberson, J.A.; Crowe, C.T (1990). Ingeniería Mecánica Fluida. Houghton Mifflin Company. ISBN 978-0-395-38124-3.
^ a b Streeter, V.L.; Wylie, E.B. (1979). Mecánica Fluida. New York: McGraw-Hill Book Company. ISBN 978-0-07-062232-6.
^ Vennard, John K. (1963). Mecánica del fluido elemental (4a edición). Nueva York: John Wiley & Sons.
^ a b c d Vischer, D.L.; Hager, W.H. (1995). Energy Dissipaters. Rotterdam: A.A. Balkema. ISBN 978-0-8247-5789-2.
^ White, Frank M. (1986). Mecánica Fluida. McGraw Hill, Inc. ISBN 978-0-07-069673-0.
^ a b c d e f g h Chanson, H. (2004). El hidráulico del flujo de canales abiertos: una introducción (2a edición). Butterworth-Heinemann. ISBN 978-0-7506-5978-9.
^ a b c d e f Chanson, H. (2009). "Current Knowledge In Hydraulic Jumps and Related Phenomena. Una encuesta de resultados experimentales" (PDF). European Journal of Mechanics B. 28 (2): 191–210. Código:2009EJMF...28..191C. doi:10.1016/j.euromechflu.2008.06.004.
^ a b Murzyn, F.; Chanson, H. (2009). " Fluctuaciones de superficie libre en saltos hidráulicos: observaciones experimentales". Experimental Thermal and Fluid Science. 33 (7): 1055-1064. doi:10.1016/j.expthermflusci.2009.06.003.
^ a b c d e f Chanson, Hubert (abril de 2012). "Consideraciones de Momento en Saltos y Bores Hidráulicos" (PDF). Journal of Irrigation and Drainage Engineering. 138 (4): 382–385. doi:10.1061/(ASCE)IR.1943-4774.0000409.
^ "Hydraulic Jump -Types y características de salto hidráulico". El Constructor. 2016-06-17. Retrieved 2019-12-26.
^ Koch, C.; Chanson, H. (2009). "Medidas deTurbulencia en Cirugias Positivas y Bores" (PDF). Journal of Hydraulic Research. 47 (1): 29–40. doi:10.3826/jhr.2009.2954. S2CID 124743367.
^ En esta sección se esbozan los enfoques a un nivel sinóptico únicamente.
^ "Pérdida de energía en un salto hidráulico". sdsu. Archivado desde el original el 17 de julio de 2007. Retrieved 1o de julio 2015.
^ Chanson, H.; Brattberg, T. (2000). "Experimental Study of the Air-Water Shear Flow in a Hydraulic Jump" (PDF). International Journal of Multiphase Flow. 26 (4): 583-607. doi:10.1016/S0301-9322(99)00016-6.
^ Murzyn, F.; Chanson, H. (2009). "Propiedades de flujo de dos fases en el salto hidráulico: revisión y perspectivas". En S. Martin y J.R. Williams (ed.). Multiphase Flow Research (PDF). Hauppauge NY, USA: Nova Science Publishers. Capítulo 9, págs. 497 a 542. ISBN 978-1-60692 a 448-8.
^ Chanson, H. (2007). "Estructura de flujo rápido en salto hidráulico" (PDF). European Journal of Mechanics B. 26 (3): 367-384. Código:2007EJMF...26..367C. doi:10.1016/j.euromechflu.2006.08.001.
^ a b Bhagat, R.K.; Jha, N.K.; Linden, P.F.; Wilson, D.I. (2018). "En el origen del salto hidráulico circular en una fina película líquida". Journal of Fluid Mechanics. 851: R5. arXiv:1712.04255. Bibcode:2018JFM...851R...5B. doi:10.1017/jfm.2018.558. S2CID 119515628.
^ Duchesne, Alexis; Limat, Laurent (2022-02-28). "Los saltos hidráulicos típicos: ¿dónde importa la tensión superficial?". Journal of Fluid Mechanics. 937. arXiv:2112.09538. Bibcode:2022JFM...937R...2D. doi:10.1017/jfm.2022.136. ISSN 0022-1120. S2CID 245329387.
^ Kostic, Svetlana; Parker, Gary (2006). "La respuesta de las corrientes de turbidez a una transición de Canyon-Fan: saltos hidráulicos internos y firmas deposiciones". Journal of Hydraulic Research. 44 (5): 631–653. doi:10.1080/00221686.2006.9521713. S2CID 53700725.
^ a b Clément, Jean Marie (2015). Bailando con el viento. Pivetta Partners. ISBN 978-8890343247.
^ "Hydraulic jump dynamics above supercell truenostorms", Science, O'Neill et al, Vol. 373, Edición 6560, Septiembre 10, 2021
^ "Cloud-surfers ride Morning Glory en el norte de Queensland". ABC Noticias3 de octubre de 2017. Retrieved 12 de junio 2018.

Contenido relacionado

Más resultados...