Rompecabezas de equilibrio
| Conocido | Objetivo | Monedas máximas para n pesajes | Número de pesajes para c monedas |
|---|---|---|---|
| Si la moneda de destino es más ligera o más pesada que otros | Identificar moneda | ||
| La moneda de destino es diferente de otros | Identificar moneda | ||
| La moneda de destino es diferente de otros, o todas las monedas son iguales | Identificar si existe una moneda única, y si es más ligero o más pesado |
Por ejemplo, al detectar una moneda disimilar en tres pesajes (), el número máximo de monedas que se pueden analizar es . Note que con pesas y monedas, no siempre es posible determinar la naturaleza de la última moneda (ya sea más pesado o más ligero que el resto), pero sólo que las otras monedas son todas iguales, lo que implica que la última moneda es la moneda disimilar. En general, con pesos, uno siempre puede determinar la identidad y la naturaleza de una sola moneda disimilar si hay o menos monedas. En el caso de tres pesajes, es posible encontrar y describir una única moneda disimilar entre una colección de monedas.
Esta versión de doce monedas del problema apareció impresa ya en 1945, y Guy y Nowakowski explican que "fue popular a ambos lados del Atlántico durante la Segunda Guerra Mundial; incluso se sugirió lanzarla sobre Alemania en un intento de sabotear su esfuerzo bélico".Problema de nueve monedas
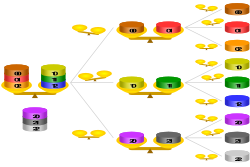
Solución
Por extensión, solo se necesitarían tres pesajes para encontrar la moneda ligera impar entre 27 monedas, y cuatro pesajes para encontrarla entre 81 monedas.
Problema de doce cuartos
Solución
- Cuatro monedas se ponen a cada lado. Hay dos posibilidades:
- 1. Un lado es más pesado que el otro. Si este es el caso, eliminar tres monedas del lado más pesado, mover tres monedas del lado más ligero al lado más pesado, y colocar tres monedas que no se pesaron la primera vez en el lado más ligero. (Recuerda qué monedas son cuáles.) Hay tres posibilidades:
- 1.a) El mismo lado que fue más pesado la primera vez es aún más pesado. Esto significa que la moneda que permaneció allí es más pesada o que la moneda que se quedó en el lado más ligero es más ligera. Balancing one of these against one of the other ten coins reveals which of these is true, thus resolution the puzzle.
- 1.b) El lado que fue más pesado la primera vez es más ligero la segunda vez. Esto significa que una de las tres monedas que pasaron del lado más ligero al lado más pesado es la moneda de luz. Para el tercer intento, pesar dos de estas monedas entre sí: si uno es más ligero, es la moneda única; si equilibran, la tercera moneda es la luz.
- 1.c) Ambos lados son iguales. Esto significa que una de las tres monedas que fue quitada del lado más pesado es la moneda pesada. Para el tercer intento, pesan dos de estas monedas entre sí: si uno es más pesado, es la moneda única; si equilibran, la tercera moneda es la pesada.
- 2. Ambos lados son iguales. Si este es el caso, las ocho monedas son idénticas y se pueden reservar. Tome las cuatro monedas restantes y coloque tres en un lado del balance. Lugar 3 de las 8 monedas idénticas en el otro lado. Hay tres posibilidades:
- 2.a) Las tres monedas restantes son más ligeras. En este caso usted ahora sabe que una de esas tres monedas es la extraña fuera y que es más ligero. Tomar dos de esas tres monedas y pesarlas entre sí. Si el balance indica que la moneda más ligera es la extraña. Si las dos monedas equilibran entonces la tercera moneda no en el balance es la extraña fuera y es más ligero.
- 2.b) Las tres monedas restantes son más pesadas. En este caso ahora sabes que una de esas tres monedas es la extraña y que es más pesada. Tomar dos de esas tres monedas y pesarlas entre sí. Si el saldo indica que la moneda más pesada es la extraña. Si las dos monedas equilibran entonces la tercera moneda que no está en el balance es la extraña hacia fuera y es más pesado.
- 2.c) Los tres saldos de monedas restantes. En este caso usted sólo tiene que pesar la moneda restante contra cualquiera de las otras 11 monedas y esto le dice si es más pesado, más ligero, o el mismo.
Variaciones
Dada una población de 13 monedas en la que se sabe que una de ellas tiene una masa diferente a la del resto, es sencillo determinar de qué moneda se trata con una balanza y tres pruebas, como se indica a continuación:
- 1) Subdivide las monedas en 2 grupos de 4 monedas y un tercer grupo con las 5 monedas restantes.
- 2) Prueba 1, Prueba los 2 grupos de 4 monedas entre sí:
- a. Si el saldo de las monedas, la moneda extraña está en la población de 5 y proceder a probar 2a.
- b. La moneda extraña está entre la población de 8 monedas, proceder de la misma manera que en el problema de 12 monedas.
- 3) Prueba 2a, Prueba 3 de las monedas del grupo de 5 monedas contra cualquier 3 monedas de la población de 8 monedas:
- a. Si el balance de 3 monedas, entonces la moneda extraña está entre la población restante de 2 monedas. Prueba una de las 2 monedas contra cualquier otra moneda; si equilibran, la moneda extraña es la última moneda no comprobada, si no equilibran, la moneda extraña es la moneda de prueba actual.
- b. Si las 3 monedas no equilibran, entonces la moneda extraña es de esta población de 3 monedas. Preste atención a la dirección del balanceo (up significa que la moneda extraña es ligera, abajo significa que es pesado). Quitar una de las 3 monedas, mover otro al otro lado del balance (remover todas las otras monedas del balance). Si el saldo se equilibra, la moneda extraña es la moneda que fue quitada. Si el balance cambia la dirección, la moneda extraña es la que se movió al otro lado, de lo contrario, la moneda extraña es la moneda que permaneció en su lugar.
Con una moneda de referencia
- 0, 1, 4, 5, 6 contra 7, 10, 11, 12, 13
- 0, 2, 4, 10, 11 contra 5, 8, 9, 12, 13
- 0, 3, 8, 10, 12 contra 6, 7, 9, 11, 13
Sin una moneda de referencia
- (entre 12 monedas A–L) concluyen si todos pesan lo mismo, o encuentran la moneda extraña y dicen si es más ligero o más pesado, o
- (entre 13 monedas A–M) encontrar la moneda extraña, y, a 12/13 probabilidad, decir si es más ligero o más pesado (para la probabilidad 1/13 restante, sólo que es diferente).
/// \\\\\ \//// / \/ \/\ //\\\\\/ \/ –\/ /- \–/ ¿Qué? - ' # /–– –– – – –– ––Como cada pesaje solo da un resultado significativo cuando el número de monedas del lado izquierdo es igual al del lado derecho, ignoramos la primera fila, de modo que cada columna tenga el mismo número de símbolos "\" y "/" (cuatro de cada uno). Las filas están etiquetadas; el orden de las monedas es irrelevante:
\/// Una luz /\\\\ un pesado /\/B light \/\ B heavy // C light \\/ C heavy #/- D light /\-D heavy - '/ E light -/ 'E heavy /–\ F light \–/ F heavy # G light // G heavy - 'H light -/ H heavy # I light // I heavy /– J light \– J heavy –/– Lámpara K– – / L luz – ‘L pesado –– M más ligero o más pesado (caso de 13 monedas), o todas las monedas pesan el mismo caso (12 monedas)Usando el patrón de resultados anterior, se puede determinar la composición de las monedas para cada pesaje; por ejemplo, el conjunto '\/– D light' implica que la moneda D debe estar en el lado izquierdo en el primer pesaje (para que ese lado sea más claro), en el lado derecho en el segundo y sin usar en el tercero:
1o peso: lado izquierdo: ADGI, lado derecho: BCFJ 2o peso: lado izquierdo: ALTO, lado derecho: ACDK 3o peso: lado izquierdo: CFHI, lado derecho: ABELLos resultados se leen de la tabla. Por ejemplo, si el lado derecho pesa menos en las dos primeras pesadas y ambos lados pesan lo mismo en la tercera, el código correspondiente «//– G pesada» implica que la moneda G es la impar y pesa más que las demás.
Generalización a múltiples escalas
En otra generalización de este problema, tenemos dos escalas de equilibrio que se pueden utilizar en paralelo. Por ejemplo, si usted sabe exactamente una moneda es diferente pero no sabe si es más pesado o más ligero que una moneda normal, entonces en rondas, puedes resolver el problema con la mayoría monedas.
Generalización a múltiples monedas desconocidas
Vamos. ser el -dimensional Espacio euclidiano y ser el producto interno de los vectores y desde Para vectores y subconjuntos las operaciones y se definen, respectivamente, como ; , , Por denotaremos la discreta [−1; 1] ; es decir, el conjunto de todas las secuencias de longitud sobre el alfabeto El set es la bola discreta del radio (en la métrica Hamming ) con centro en el punto Pesos relativos de objetos son dados por un vector que define las configuraciones de pesos de los objetos: t objeto tiene peso estándar si el peso del t objeto es mayor (smaller) por un valor constante (no conocido) si (respectivamente, ). El vector caracteriza los tipos de objetos: el tipo estándar, el tipo no estándar (es decir, configuraciones de tipos), y no contiene información sobre pesos relativos de objetos no estándar.
Un peso (un cheque) es dado por un vector el resultado de un peso para una situación es El peso dado por un vector tiene la siguiente interpretación: para un cheque dado el t objeto participa en el pesaje si ; se pone en el balance de la izquierda si y se pone en la cacerola derecha si Para cada pesaje , ambas sartenes deben contener el mismo número de objetos: si en alguna cacerola el número de objetos es menor de lo que debe ser, entonces recibe algunos objetos de referencia. El resultado de un pesaje describe los siguientes casos: el saldo si , la sartén izquierda supera a la derecha si , y la cacerola derecha supera la izquierda si La falta de información inicial sobre la distribución de pesos de un grupo de objetos se caracteriza por el conjunto de distribuciones admisibles de pesos de objetos que también se llama el conjunto de situaciones admisibles, los elementos se llaman situaciones admisibles.
Cada pesaje induce la partición del conjunto por el avión (hiperplano) en tres partes , y define la partición correspondiente del conjunto Donde
Definición 1. Un algoritmo de pesaje (WA) de longitud es una secuencia Donde es la función que determina el cheque a cada uno a paso, del algoritmo de los resultados de pesos en los pasos anteriores ( es un cheque inicial dado).
Vamos. ser el conjunto de todos - Síndromes y ser el conjunto de situaciones con el mismo síndrome i.e., ;
Definición 2. A WA se dice: a) identificar las situaciones en un conjunto si la condición está satisfecho para todos b) identificar los tipos de objetos en un conjunto si la condición está satisfecho para todos
Se prueba en que para los llamados conjuntos adecuados un algoritmo de identificación de los tipos identifica también las situaciones
Como ejemplo, los algoritmos dinámicos perfectos (dos cascadas) con parámetros se construyen en los que corresponden a los parámetros del código Golay ternario perfecto (código Virtakallio-Golay). Al mismo tiempo, se establece que una WA estática (es decir, código de ponderación) con los mismos parámetros no existe.
Cada uno de estos algoritmos usando 5 pesajes encuentra entre 11 monedas hasta dos monedas falsificadas que podrían ser más pesados o más ligeros que las monedas reales por el mismo valor. En este caso el dominio de incertidumbre (el conjunto de situaciones admisibles) contiene situaciones, es decir, la ES construida se encuentra en el límite de Hamming y en este sentido es perfecto.
Hasta la fecha no se sabe si hay otra WA perfecta que identifique las situaciones en para algunos valores . Además, no se sabe si para algunos existen soluciones para la ecuación (correspondiendo al límite de Hamming para códigos ternarios) que es, obviamente, necesario para la existencia de una WA perfecta. Sólo se sabe que no hay una WA perfecta, y para esta ecuación tiene la solución única que determina los parámetros de la ES perfecta construida.
Referencias
- ^ Smith, C.A.B. (febrero de 1947). "El problema de la moneda falsificada". Boletín matemático. 31 (293): 31–39. doi:10.2307/3608991. JSTOR 3608991.
- ^ a b Grossman, Howard D. (septiembre–diciembre de 1945). "El problema de doce monedas". Scripta Mathematica. 11 ()3-4): 360 –361.
- ^ a b Guy, Richard; Nowakowski, Richard (febrero de 1995). "Problemas de lucha contra el dolor". American Mathematical Monthly. 102 2): 164 –167. doi:10.1080/00029890.1995.11990553.
- ^ Dyson, Freeman J. (1946). "1931. El problema de los peniques". La Gaceta Matemática. 30 (291): 231 –234. JSTOR 3611225.
- ^ "Math Forum - Pregúntele al Dr. Math". mathforum.org. Archivado desde el original el 19 de diciembre de 2002.
- ^ Khovanova, Tanya (2013). "Solución al problema de la moneda falsificada y su generalización". arXiv:1310.7268 [Math.HO].
- ^ a b c Chudnov, Alexander M. (2015). "Pesar algoritmos de clasificación e identificación de situaciones". Discreta Matemáticas y Aplicaciones. 25 2): 69 –81. doi:10.1515/dma-2015-0007. S2CID 124796871.
Enlaces externos
- El gran rompecabezas de pesas en NRICH














![{\displaystyle [\mathrm {e} ^{1},\mathrm {e} ^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/720e187783b3816d08327b56ac6fe5cf73976295)

























![{\displaystyle s(\mathrm {x};\mathrm {h})=sign([\mathrm {x};\mathrm {h} ]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/baf6786534be971bad9d1e2015e7490bd6599d2d)





![{\displaystyle r(\mathrm {h})=[\mathrm {h};1,\dots1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bd6c8a71c637921d7d2283b858ea1f5b051542e)






![{\displaystyle [\mathrm {x};\mathrm {h} ]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5196f49ec53845f777a09f58d327196e180449a0)

































