Rombo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Cuadrilateral en el que todas las partes tienen la misma longitud

El rhombus tiene un cuadrado como un caso especial, y es un caso especial de una cometa y paralelograma.

En geometría euclidiana plana, un rombo (plural rombos o rombos) es un cuadrilátero cuyos cuatro lados tienen todos la misma longitud. Otro nombre es cuadrilátero equilátero, ya que equilátero significa que todos sus lados tienen la misma longitud. El rombo a menudo se llama "diamante", por el palo de diamantes en los naipes que se asemeja a la proyección de un diamante octaédrico, o un rombo, aunque el primero a veces se refiere específicamente a un rombo con un ángulo de 60° (al que algunos autores llaman calisson por el dulce francés; véase también Polyiamond), y este último a veces se refiere específicamente a un rombo con un ángulo de 45°.

Todos los rombos son simples (no se cortan a sí mismos) y son un caso especial de un paralelogramo y una cometa. Un rombo con ángulos rectos es un cuadrado.

Etimología

La palabra "rombo" proviene del griego antiguo: ῥόμβος, romanizado: rombos, que significa algo que gira, que se deriva del verbo ῥέμβω, romanizado: rhémbō, que significa "dar vueltas y vueltas". La palabra fue utilizada tanto por Euclides como por Arquímedes, quienes utilizaron el término "rombo sólido" para un bicono, dos conos circulares rectos que comparten una base común.

La superficie a la que nos referimos como rombo hoy es una sección transversal del bicono en un plano a través de los vértices de los dos conos.

Caracterizaciones

Un cuadrilátero simple (que no se corta a sí mismo) es un rombo si y solo si es cualquiera de los siguientes:

un paralelograma en el que un bisecto diagonal es un ángulo interior
un paralelograma en el que al menos dos partes consecutivas son iguales en longitud
a paralelograma en el que las diagonales son perpendiculares (paralelograma ortodiagonal)
un cuadrilátero con cuatro lados de igual longitud (por definición)
un cuadrilátero en el que las diagonales son perpendiculares y se bisecan entre sí
un cuadrilátero en el que cada bisecto diagonal dos ángulos interiores opuestos
a quadrilateral ABCD poseer un punto P en su plano tal que los cuatro triángulos ABP, BCP, CDP, y DAP son todos congruentes
a quadrilateral ABCD en que los círculos en triángulos ABC, BCD, CDA y DAB tener un punto común

Propiedades básicas

Todo rombo tiene dos diagonales que conectan pares de vértices opuestos y dos pares de lados paralelos. Usando triángulos congruentes, se puede demostrar que el rombo es simétrico en cada una de estas diagonales. De ello se deduce que cualquier rombo tiene las siguientes propiedades:

Los ángulos opuestos de un rombo tienen igual medida.
Las dos diagonales de un rombo son perpendiculares; es decir, un rombo es un cuadrilátero ortodiagonal.
Sus diagonales bisect ángulos opuestos.

La primera propiedad implica que todo rombo es un paralelogramo. Por lo tanto, un rombo tiene todas las propiedades de un paralelogramo: por ejemplo, los lados opuestos son paralelos; los ángulos adyacentes son suplementarios; las dos diagonales se bisecan; cualquier línea que pasa por el punto medio biseca el área; y la suma de los cuadrados de los lados es igual a la suma de los cuadrados de las diagonales (la ley del paralelogramo). Denotando así el lado común como a y las diagonales como p y q, en todo rombo

displaystyle 4a^{2}=p^{2}+q^{2}.

No todo paralelogramo es un rombo, aunque cualquier paralelogramo con diagonales perpendiculares (la segunda propiedad) es un rombo. En general, cualquier cuadrilátero con diagonales perpendiculares, una de las cuales es un eje de simetría, es una cometa. Todo rombo es una cometa, y todo cuadrilátero que es a la vez una cometa y un paralelogramo es un rombo.

Un rombo es un cuadrilátero tangencial. Es decir, tiene un círculo inscrito que es tangente a los cuatro lados.

Un rombo. Cada ángulo marcado con un punto negro es un ángulo recto. La altura h es la distancia perpendicular entre los dos lados no adyacentes, que equivale al diámetro del círculo inscrito. Las diagonales de longitudes p y q son los segmentos de línea de puntos rojos.

Diagonales

La longitud de las diagonales p = AC y q = BD se puede expresar en términos del lado del rombo a y el ángulo de un vértice α como

{displaystyle p=a{sqrt {2+2cos {alpha }}}}

{displaystyle q=a{sqrt {2-2cos {alpha }}}.}

Estas fórmulas son una consecuencia directa de la ley de los cosenos.

Inradio

El inradio (el radio de un círculo inscrito en el rombo), denotado por $r$ , se puede expresar en términos de las diagonales $p$ y $q$ como

{displaystyle r={frac {pcdot q}{2{sqrt {p^{2}+q^{2}}}}},}

o en términos de la longitud del lado $a$ y cualquier ángulo de vértice $α$ o $β$ como

{displaystyle r={frac {asin alpha }{2}}={frac {asin beta }{2}}.}

Área

Como en todos los paralelogramos, el área K de un rombo es el producto de su base por su altura (h). La base es simplemente cualquier longitud de lado a:

{displaystyle K=acdot h.}

El área también se puede expresar como la base al cuadrado por el seno de cualquier ángulo:

{displaystyle K=a^{2}cdot sin alpha =a^{2}cdot sin beta}

o en términos de la altura y un ángulo de vértice:

{displaystyle K={frac {h^{2}}{sin alpha }},}

o como la mitad del producto de las diagonales p, q:

{displaystyle K={frac {pcdot q}{2}},}

o como el semiperímetro por el radio del círculo inscrito en el rombo (inradius):

{displaystyle K=2acdot r.}

Otra forma, en común con los paralelogramos, es considerar dos lados adyacentes como vectores, formando un bivector, por lo que el área es la magnitud del bivector (la magnitud del producto vectorial de los dos vectores), que es el determinante de los dos vectores' Coordenadas cartesianas: K = x₁y₂ – x₂y₁.

Propiedades duales

El polígono dual de un rombo es un rectángulo:

Un rhombus tiene todos los lados iguales, mientras que un rectángulo tiene todos los ángulos iguales.
Un rhombus tiene ángulos opuestos iguales, mientras que un rectángulo tiene lados opuestos iguales.
Un rhombus tiene un círculo inscrito, mientras que un rectángulo tiene un círculo.
Un rhombus tiene un eje de simetría a través de cada par de ángulos de vértice opuestos, mientras que un rectángulo tiene un eje de simetría a través de cada par de lados opuestos.
Las diagonales de un rombo se intersecten en ángulos iguales, mientras que las diagonales de un rectángulo son iguales en longitud.
La figura formada al unir los puntos intermedios de los lados de un rombo es un rectángulo, y viceversa.

Ecuación cartesiana

Los lados de un rombo centrado en el origen, con diagonales que caen sobre un eje, consisten en todos los puntos (x, y) que satisfacen

{displaystyle left|{frac {x}{a}}right|!+left|{frac {y}{b}}right|!=1.}

Los vértices están en ${displaystyle (pm a,0)}$ y ${displaystyle (0,pm b).}$ Este es un caso especial de la superellipse, con exponente 1.

Otras propiedades

Uno de los cinco tipos de celosía 2D es la celosía rhombic, también llamada rejilla rectangular centrada.
Los rhombis idénticos pueden inclinar el plano 2D de tres maneras diferentes, incluyendo, para el rhombus de 60°, el azulejo de rombille.

Como revestimientos cuadrados topológicos		Al nivel de 30-60 grados

Los análogos tridimensionales de un rombo incluyen la bipirámide y el bicono como una superficie de revolución.

Como las caras de un poliedro

Los poliedros convexos con rombos incluyen el conjunto infinito de zonoedros rómbicos, que pueden verse como envolventes proyectivas de hipercubos.

Un rhombohedron (también llamado hexahedro rhombic) es una figura tridimensional como un cuboide (también llamado paralelo rectangular), excepto que sus 3 pares de caras paralelas son de hasta 3 tipos de rhombi en lugar de rectángulos.
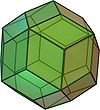
El dodecaedro rhombic es un poliedro convexo con 12 rhombi congruente como sus caras.
El triacontahedro rhombic es un poliedro convexo con 30 rhombi dorado (rhombi cuyas diagonales están en la relación dorada) como sus caras.
El gran triacontahedro rhombic es un isohedral no convexo, poliedro isotoxal con 30 caras rhombic intersectando.
El hexecontahedron rhombic es una estelación del triacontahedro rhombic. No es convexo con 60 caras rhombic doradas con simetría icosahedral.
El enneacontahedro rhombic es un poliedro compuesto por 90 caras rhombic, con tres, cinco o seis encuentros rhombi en cada vértice. Tiene 60 rhombi ancho y 30 delgados.
El icosahedro rhombic es un poliedro compuesto por 20 caras rhombic, de las cuales tres, cuatro o cinco se encuentran en cada vértice. Tiene 10 caras en el eje polar con 10 caras siguiendo el ecuador.

Ejemplo de polihedra con todas las caras rhombic
Isohedral		Isohedral golden rhombi		2-isohedral	3-isohedral

Trigonal trapezohedron	Rhombic dodecahedron	Triacontahedron Rhombic	Rhombic icosahedron	Rhombic enneacontahedron	Rhombohedron

Contenido relacionado

Más resultados...